Skip to main content
SpringerLink
Log in

On LQR controller design for an inverted pendulum stabilization

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

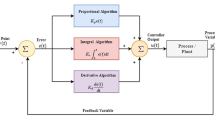
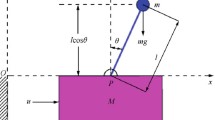
Linear quadratic regulator (LQR) is a control strategy that has found a wide range of applications. Even though LQR possesses high performance and good robustness, designing these controllers has been proved to be difficult, primarily due to lacking of a proper selection methodology to select Q and R weighing matrices. In this paper, we propose a deterministic approach to their selection, giving the designer actual control over performance parameters. This method has been by validated by applying it to the stabilization of a practical inverted pendulum system. MATLAB simulation results reveal that the proposed method results in good stability, settling time and overshoot.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Availability

Data used in this work is available in the public domain.

References

  1. Athans M, Falb PL (2013) Optimal control: an introduction to the theory and its applications. Courier Corporation, Chelmsford

    Google Scholar 

  2. Sargent R (2000) Optimal control. J Comput Appl Math 124(1–2):361–371

    Article  MathSciNet  MATH  Google Scholar 

  3. Comissiong D, Sooknanan J (2018) A review of the use of optimal control in social models. Int J Dyn Control 6(4):1841–1846

    Article  Google Scholar 

  4. James M (2021) Optimal quantum control theory. Ann Rev Control Robot Auton Syst 4:343–367

    Article  Google Scholar 

  5. Maciejowski JM (1989) Multivariable feedback design. Electronic systems engineering series

  6. Safonov M, Athans M (1977) Gain and phase margin for multiloop LQG regulators. IEEE Trans Autom Control 22(2):173–179

    Article  MathSciNet  MATH  Google Scholar 

  7. Priyambodo TK, Dhewa OA, Susanto T (2020) Model of linear quadratic regulator (LQR) control system in waypoint flight mission of flying wing UAV. J Telecommun Electron Comput Eng (JTEC) 12(4):43–49

    Google Scholar 

  8. Priess MC, Conway R, Choi J, Popovich JM, Radcliffe C (2014) Solutions to the inverse LQR problem with application to biological systems analysis. IEEE Trans Control Syst Technol 23(2):770–777

    Article  Google Scholar 

  9. CRAMER E, LEE T (1992) Test flight of LQR missile guidance. In: Astrodynamics conference, p 4532

  10. Starin SR, Yedavalli R, Sparks AG (2001) Design of a LQR controller of reduced inputs for multiple spacecraft formation flying. In: Proceedings of the 2001 American control conference.(Cat. No. 01CH37148), vol 2. IEEE, pp 1327–1332

  11. Priyambodo TK, Dhewa OA, Susanto T (2020) Model of linear quadratic regulator control system in waypoint flight mission of flying wing UAV. J Telecommun Electron Comput Eng (JTEC) 12(4):43–49

    Google Scholar 

  12. Elkhatem AS, Engin SN (2022) Robust LQR and LQR-PI control strategies based on adaptive weighting matrix selection for a UAV position and attitude tracking control. Alex Eng J 61(8):6275–6292

    Article  Google Scholar 

  13. Yu W, Li J, Yuan J, Ji X (2021) LQR controller design of active suspension based on genetic algorithm. In: 2021 IEEE 5th information technology, networking, electronic and automation control conference (ITNEC), vol 5. IEEE, pp 1056–1060

  14. Haiying W, Hongwen L, Jinlin J, Rui X (2010) LQR control of circular-rail double inverted pendulum based on genetic algorithm. J North Univ China 2:132–135

    Google Scholar 

  15. Shen P (2014) Application of genetic algorithm optimization LQR weighting matrices control inverted pendulum. In: Applied mechanics and materials, vol 543–547, pp 1274–1277. https://doi.org/10.4028/www.scientific.net/amm.543-547.1274.

  16. Kukreti S, Kumar M, Cohen K (2016) Genetically tuned LQR based path following for UAVs under wind disturbance. In: 2016 International conference on unmanned aircraft systems (ICUAS). IEEE, pp 267–274

  17. Bhushan R, Chatterjee K, Shankar R (2016) Comparison between GA-based LQR and conventional LQR control method of DFIG wind energy system. In: 2016 3rd international conference on recent advances in information technology (RAIT). IEEE, pp 214–219

  18. Tan W (2012) An improved method for rectilinear double inverted pendulum LQR controller parameter optimization. J Chongqing Univ Technol (Natl Sci) 85–88

  19. Wang H, Zhou H, Wang D, Wen S (2013) Optimization of LQR controller for inverted pendulum system with artificial bee colony algorithm. In: Proceedings of the 2013 international conference on advanced mechatronic systems. IEEE, pp 158–162

  20. Peng Y, Chen Y (2014) Optimal design of the LQR controller based on the improved shuffled frog-leaping algorithm. CAAI Trans Intell Syst 9(4):480–484

    Google Scholar 

  21. Almobaied M, Eksin I, Guzelkaya M (2016) Design of LQR controller with big bang-big crunch optimization algorithm based on time domain criteria. In: 2016 24th Mediterranean conference on control and automation (MED). IEEE, pp 1192–1197

  22. Deng X, Sun X, Liu R, Wei W (2017) Optimal analysis of the weighted matrices in LQR based on the differential evolution algorithm. In: 2017 29th Chinese control and decision conference (CCDC). IEEE, pp 832–836

  23. Nekoui MA, Bozorgi HHJ (2011) Weighting matrix selection method for LQR design based on a multi-objective evolutionary algorithm. In: Advanced materials research, 383–390. Trans Tech Publication, pp 1047–1054. https://doi.org/10.4028/www.scientific.net/amr.383-390.1047

  24. Oral O, Cetin L, Uyar E (2010) A novel method on selection of Q and R matrices in the theory of optimal control. Int J Syst Control 1(2):84–92

  25. Kumar EV, Jerome J, Srikanth K (2014) Algebraic approach for selecting the weighting matrices of linear quadratic regulator. In: 2014 international conference on green computing communication and electrical engineering (ICGCCEE). IEEE, pp 1–6

  26. Kafetzis I, Moysis L (2017) Inverted pendulum: a system with innumerable applications. In: School of mathematical sciences. http://ikee.lib.auth.gr/record/288541?ln=en

  27. Hehn M, D’Andrea R (2011) A flying inverted pendulum. In: 2011 IEEE international conference on robotics and automation. IEEE, pp 763–770

  28. Anh N, Matsuhisa H, Viet L, Yasuda M (2007) Vibration control of an inverted pendulum type structure by passive mass-spring-pendulum dynamic vibration absorber. J Sound Vib 307(1–2):187–201

    Article  Google Scholar 

  29. Ogata K et al (2010) Modern control engineering, vol 5. Prentice hall Upper Saddle River, New Jersey

    MATH  Google Scholar 

  30. Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning (1st. ed.). Addison-Wesley Longman Publishing Co., Inc., USA. https://dl.acm.org/doi/10.5555/534133

  31. Conn A, Gould N, Toint P (1997) A globally convergent Lagrangian barrier algorithm for optimization with general inequality constraints and simple bounds. Math Comput 66(217):261–288

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

The authors did not receive funding from any organization for the submitted work.

Author information

Author notes

  1. S. J. Chacko and R. J. Abraham contributed equally to this work.

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Space Science and Technology, Thiruvananthapuram, Kerala, 695547, India

    Sanjay Joseph Chacko

  2. Department of Avionics, Indian Institute of Space Science and Technology, Thiruvananthapuram, Kerala, 695547, India

    Rajesh Joseph Abraham

Authors
  1. Sanjay Joseph Chacko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajesh Joseph Abraham
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally to the work.

Corresponding author

Correspondence to Rajesh Joseph Abraham.

Ethics declarations

Conflict of interest

There are no conflicts of interest/competing interests.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chacko, S.J., Abraham, R.J. On LQR controller design for an inverted pendulum stabilization. Int. J. Dynam. Control 11, 1584–1592 (2023). https://doi.org/10.1007/s40435-022-01079-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-022-01079-0

Keywords

Search

Navigation