Adaptive fuzzy backstepping hierarchical sliding mode control for six degrees of freedom overhead crane

Abstract

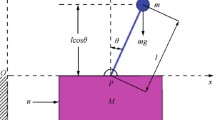
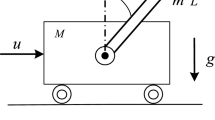
Most overhead crane control studies attempt to position the payload accurately and minimize its horizontal swing without considering axial oscillation. The axial vibration caused by the lifting rope’s elasticity significantly affects the actuators’ reliability and the system’s overall performance over time. In this paper, a novel overhead crane model is developed to describe an actual crane’s behavior more closely by further considering the effect of axial payload oscillation. Furthermore, an adaptive fuzzy backstepping hierarchical sliding mode controller is designed to guarantee precise movements and reduce vibrations of payload in both horizontal and vertical directions under complex conditions, such as unknown external disturbances and cable elasticity. Three inputs consisting of the trolley-moving force, the bridge-pulling force, and the payload-hoisting torque stabilize six outputs simultaneously, including trolley motion, bridge travel, hoisting drum rotation, two payload swings, and axial payload oscillation. The controller is first designed using the backstepping hierarchical sliding mode control strategy. This controller’s parameters are then adjusted online using a fuzzy logic system, ensuring system states’ stability on the sliding surface. The system’s stability is analyzed and proved mathematically by LaSalle’s principle. Several simulations on MATLAB/Simulink have been conducted with constant or trapezoidal reference signals, with and without external disturbances. These simulation results show the proposed method’s effectiveness, such as motion precision, minor load swings, and minimal axial oscillation.

Appendices

The coefficients of matrices

1. The coefficients of matrix M.

$$\begin{aligned}&l = \delta + \Delta \delta + r{\vartheta _x} + r\psi \\ {m_{11}}&= {m_c} + {m_t}\\ {m_{12}}&= {m_{21}} = {m_{51}} = {m_{15}} = 0\\ {m_{13}}&= {m_{31}} = {m_c}r\sin \left( {{\vartheta _x}} \right) \\ {m_{14}}&= {m_{41}} = {m_c}l\cos \left( {{\vartheta _x}} \right) \\ {m_{16}}&= {m_{61}} = {m_c}\sin \left( {{\vartheta _x}} \right) \\ {m_{22}}&= {m_c} + {m_b} + {m_t}\\ {m_{23}}&= {m_{32}} = {m_c}r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ {m_{24}}&= {m_{42}} = \\&={m_c}\left( {r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - l\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {m_{25}}&= {m_{52}} = {m_c}l\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ {m_{26}}&= {m_{62}} = {m_c}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ {m_{33}}&= J + {m_c}{r^2}\\ {m_{34}}&= {m_{43}} = {m_c}{r^2}{\text {co}}{{\text {s}}^2}\left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ {m_{35}}&= {m_{53}} = \frac{1}{4}{m_c}{r^2}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ {m_{36}}&= {m_{63}} = {m_c}r\\ {m_{44}}&= {m_c}\left( \begin{aligned} {l^2} + {r^2}{\sin ^2}\left( {{\vartheta _y}} \right) {\text {co}}{{\text {s}}^2}\left( {{\vartheta _x}} \right) - \\ r\delta {\sin ^2}\left( {{\vartheta _y}} \right) \sin \left( {2{\vartheta _x}} \right) \\ \end{aligned} \right) \\ {m_{45}}&= {m_{54}} = \frac{1}{2}{m_c}rl\sin \left( {2{\vartheta _y}} \right) {\text {cos}}\left( {2{\vartheta _x}} \right) \\ {m_{46}}&= {m_{64}} = {m_c}r{\sin ^2}\left( {{\vartheta _y}} \right) {\cos ^2}\left( {{\vartheta _x}} \right) \\ {m_{55}}&= {m_c}\left( \begin{aligned} {l^2}{\cos ^2}\left( {{\vartheta _x}} \right) + {r^2}{\sin ^2}\left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) - \\ rl\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {m_{56}}&= {m_{65}} = \frac{1}{4}{m_c}r\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ {m_{66}}&= {m_c} \end{aligned}$$

2. The coefficients of matrix C

$$\begin{aligned} {c_{11}}&= {c_{21}} = {c_{31}} = {c_{33}} = {c_{41}} = {c_{51}} = {c_{15}} = {c_{61}} = 0\\ {c_{12}}&= {c_{22}} = {c_{32}} = {c_{42}} = {c_{52}} = 0\\ {c_{62}}&= {c_{36}} = {c_{63}} = {c_{66}} = 0\\ {c_{13}}&= 2{m_c}r{{\dot{\vartheta }} _x}\cos \left( {{\vartheta _x}} \right) \\ {c_{14}}&= {m_c}\left( {r{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) - l{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) } \right) \\ {c_{16}}&= 2{m_c}{{\dot{\vartheta }} _x}\cos \left( {{\vartheta _x}} \right) \\ {c_{23}}&= 2{m_c}r\left( \begin{aligned} {{\dot{\vartheta }} }_y\cos \left( {\vartheta _x} \right) \cos \left( {\vartheta _y} \right) - \\ {{\dot{\vartheta }} }_x\sin \left( {\vartheta _x} \right) \sin \left( {\vartheta _y} \right) \\ \end{aligned} \right) \\ {c_{24}}&= {m_c}\left( \begin{aligned} 2r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{25}}&= - {m_c}l\left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{26}}&= 2{m_c}\left( {{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - {{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {c_{34}}&= {m_c}r\left( \begin{aligned} - l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ \frac{l}{2}{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _x}} \right) - \\ \frac{r}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) \left( {1 + {{\sin }^2}\left( {{\vartheta _x}} \right) } \right) \\ \end{aligned} \right) \\ {c_{35}}&= {m_c}r\left( \begin{aligned} \frac{r}{2}{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) -\\ l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - \\ \frac{l}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{43}}&= {m_c}r\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{44}}&= {m_c}\left( \begin{aligned} - \left( \begin{aligned} l\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ r\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} 2r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ lr{{{\dot{\vartheta }} }_x}{\cos ^2}\left( {{\vartheta _x}} \right) - {l^2}{{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _x}} \right) - \\ {l^2}{{{\dot{\vartheta }} }_y}{\sin ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ + \frac{{{l^2}}}{2}{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) + \\ lr{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{45}}&= {m_c}\left( \begin{aligned} \left( \begin{aligned} {l^2}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ rl\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ {l^2}{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) - \\ rl{{{\dot{\vartheta }} }_y}{\sin ^2}\left( {{\vartheta _x}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{46}}&= {m_c}\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_x} + r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{53}}&= 2{m_c}r\left( \begin{aligned} l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - \\ r{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \sin \left( {{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{54}}&= {m_c}\left( \begin{aligned} l\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \times \\ \left( \begin{aligned} 2r\left( \begin{aligned} {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ {{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) - \\ l {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \left( {r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - l\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \times \\ \left( \begin{aligned} l\left( \begin{aligned} {{{\dot{\vartheta }} }_x}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ 2{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) + \\ r{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \end{aligned} \right) \\ {c_{55}}&= {m_c}\left( \begin{aligned} \left( \begin{aligned} r{{{\dot{\vartheta }} }_y}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) - \\ l{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \times \\ \left( \begin{aligned} r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) - \\ l\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) - \\ {l^2}\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \times \\ \left( \begin{aligned} 2{{{\dot{\vartheta }} }_x}\sin \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \\ {{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ \end{aligned} \right) \\ {c_{56}}&= {m_c}\left( \begin{aligned} 2l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) - r{{{\dot{\vartheta }} }_x}{\sin ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) - \\ r{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{64}}&= {m_c}\left( \begin{aligned} - l{{{\dot{\vartheta }} }_x} - \frac{1}{2}r{{{\dot{\vartheta }} }_x}\sin \left( {2{\vartheta _x}} \right) {\sin ^2}\left( {{\vartheta _y}} \right) + \\ \frac{1}{2}l{{{\dot{\vartheta }} }_y}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) + \\ r{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \\ {c_{65}}&= {m_c}\left( \begin{aligned} - l{{{\dot{\vartheta }} }_y}{\cos ^2}\left( {{\vartheta _x}} \right) + r{{{\dot{\vartheta }} }_y}\cos \left( {{\vartheta _x}} \right) \times \\ \sin \left( {{\vartheta _y}} \right) {\cos ^2}\left( {{\vartheta _y}} \right) - \\ \frac{l}{2}{{{\dot{\vartheta }}}_{x}}\sin \left( {2{\vartheta _x}} \right) \sin \left( {2{\vartheta _y}} \right) \\ \end{aligned} \right) \end{aligned}$$

3. The coefficients of vector G.

$$\begin{aligned} {g_1}&= {m_c}gr\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) \\ {g_2}&= - {m_c}gl\sin \left( {{\vartheta _x}} \right) {\text {cos}}\left( {{\vartheta _y}} \right) \\ {g_3}&= - {m_c}g\left( {l\sin \left( {{\vartheta _y}} \right) {\text {cos}}\left( {{\vartheta _x}} \right) - r\sin \left( {{\vartheta _x}} \right) \sin \left( {{\vartheta _y}} \right) } \right) \\ {g_4}&= {m_c}g\cos \left( {{\vartheta _x}} \right) \cos \left( {{\vartheta _y}} \right) + \rho \Delta \delta \end{aligned}$$

Proof of system stability

Let’s begin with following assumption.

Assumption 1

The backstepping control errors ${\xi _1},{\text { }}{\xi _2}$ in (19) and its time derivative are bounded, i.e., there exists a large enough number $A \in {\mathbb {R}}$ such that ${\left\| {{\xi _1}} \right\| }, {\left\| {{\xi _2}} \right\| }, {\left\| {{{{\dot{\xi }} }_1}} \right\| },{\left\| {{{{\dot{\xi }} }_2}} \right\| } \leqslant A < + \infty$

This assumption is suitable for most natural systems, as states have a certain allowable limit.

Theorem 2

If the control law is defined as in (38) and the sliding surfaces are defined as in (25), (34), then, the subsystems and the entire system in (24) will stabilize asymptotically at the origin, i.e.,

1) $\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _1} = {0} ,{\text { }}\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _2} = {0}$

2) $\mathop {\lim }\limits _{t \rightarrow \infty } S = {0}$

where $u_{11\mathrm{eq}}$ and $u_{12\mathrm{eq}}$ are defined as in (32) and (33), respectively; $u_{11\mathrm{sw}}$ and $u_{12\mathrm{sw}}$ are determined to satisfy (43).

Proof

Applying the inequality of the quadratic form to (44), it yields:

$$\begin{aligned} {\dot{V}}_S&= - {S^T}\Upsilon {\lambda _1}S - {S^T}\Upsilon {\lambda _2}\mathrm{sign}\left( S \right) \nonumber \\&\leqslant - \lambda _{\min }^{\Upsilon {\lambda _1}}{\left\| S \right\| ^2} - \eta {S^T}\mathrm{sign}(S) \leqslant 0 \end{aligned}$$

(B1)

where $\lambda _{\min }^{\Upsilon {\lambda _1}}$ is the smallest eigenvalue of the coefficient matrix $\Upsilon {\lambda _1}$, and $\eta$ is any eigenvalue of the matrix $\Upsilon {\lambda _2}$.

Integrating both sides of (B1) with time, one obtains:

$$\begin{aligned} \int _0^t {{{\dot{V}}_S}d\tau }&\leqslant - \lambda _{\min }^{\Upsilon {\lambda _1}}\int _0^t {{\left\| S \right\| }^2}d\tau \nonumber \\ {}&- \eta \int _0^t {S^T}\mathrm{sign}(S) d\tau \nonumber \\ {V_S}\left( t \right)&\leqslant {V_S}\left( 0 \right) - \lambda _{\min }^{\Upsilon {\lambda _1}}\int _0^t {{\left\| S \right\| }^2}d\tau \nonumber \\ - \eta \int _0^t {S^T}\mathrm{sign}(S) d\tau&\leqslant {V_S}\left( 0 \right) \end{aligned}$$

(B2)

$\square$

From (35) and (36), it can be deduced that:

$$\begin{aligned} \lambda _{\min }^\Upsilon {\left\| S \right\| ^2}&\leqslant \frac{1}{2}{\left( {\int _0^t {Sd\tau } } \right) ^T}\Upsilon {\left( {1 - \gamma } \right) ^p}\Xi \int _0^t {Sd\tau } \nonumber \\&+\frac{1}{2}{S^T}\Upsilon S \leqslant {V_S}\left( 0 \right) \end{aligned}$$

(B3)

Inequality in (B3) shows that the energy inside the system is constantly decreasing. It can be seen that if $\left\| S \right\| \rightarrow 0$ as $t \rightarrow \infty$, the system state gradually approaches and stabilizes at its reference state.

In addition, given Assumption, it can be clearly seen that:

$$\begin{aligned} \left\| S \right\| = \left\| {{\alpha _1}{\xi _1} + {\alpha _2}{\xi _2}} \right\| \leqslant \left\| {{\alpha _1}{\xi _1}} \right\| + \left\| {{\alpha _2}{\xi _2}} \right\| < +\infty \end{aligned}$$

(B4)

Considering the following expressions:

$$\begin{aligned} \left\{ {\begin{matrix} {{\Phi _1} = {c_1}{\xi _1} + {\xi _2}} \\ {{\Phi _2} = {c_2}{\xi _1} + {\xi _2}} \end{matrix}} \right. \end{aligned}$$

(B5)

where ${c_1},{c_2} \in {\mathbb {R}^{3 \times 3}}$ are any positive diagonal matrices, and ${c_1} \ne {c_2}$.

Without loss of generality, it may be assumed that $\left\| {{c_1}} \right\| > \left\| {{c_2}} \right\|$.

Based on the inequality of the quadratic form, it can be deduced that:

$$\begin{aligned}&\begin{aligned} 0 \leqslant {\left( {\int _0^{ + \infty } {{\Phi _1}d\tau } } \right) ^T}\int _0^{ + \infty } {{\Phi _1}d\tau } \leqslant \int _0^{ + \infty } {\Phi _1^T{\Phi _1}d\tau } \\ = \int _0^{ + \infty } {\left( {\xi _1^Tc_1^T{c_1}{\xi _1} + \xi _2^T{\xi _2}} \right) } d\tau + 2\int _0^{ + \infty } {\xi _1^Tc_1^T{\xi _2}d\tau } \\ \end{aligned} \\&\begin{aligned} 0 \leqslant {\left( {\int _0^{ + \infty } {{\Phi _2}d\tau } } \right) ^T}\int _0^{ + \infty } {{\Phi _2}d\tau } \leqslant \int _0^{ + \infty } {\Phi _2^T{\Phi _2}d\tau } \\ = \int _0^{ + \infty } {\left( {\xi _1^Tc_2^T{c_2}{\xi _1} + \xi _2^T{\xi _2}} \right) } d\tau + 2\int _0^{ + \infty } {\xi _1^Tc_2^T{\xi _2}} d\tau \\ \end{aligned} \end{aligned}$$

On the other hand,

$$\begin{aligned}&\int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau } \nonumber \\&=\int _0^{ + \infty } {\xi _1^T\left( {c_1^T{c_1} - c_2^T{c_2}} \right) {\xi _1}d\tau }+ \nonumber \\&\quad + 2\int _0^{ + \infty } {\xi _1^T\left( {c_1^T - c_2^T} \right) } {\xi _2}d\tau \end{aligned}$$

(B6)

Substituting ${\xi _2} = {\Phi _1} - {c_1}{\xi _1}$ into (B6), and note that $c_2^T{c_1} = c_1^T{c_2}$, simplifying yields:

$$\begin{aligned}&\int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau } \nonumber \\&=2\int _0^{ + \infty } {{{\xi }}{{_1^T}}\left( {c_1^T - c_2^T} \right) {\Phi _1}d\tau }+ \nonumber \\&+\quad \int _0^{ + \infty } {{{\xi }}_1^T{{\left( {{c_1} - {c_2}} \right) }^T}\left( {{c_1} - {c_2}} \right) {{{\xi }}_1}d\tau } \end{aligned}$$

(B7)

Because $\left\| {{c_1}} \right\| > \left\| {{c_2}} \right\|$, so we have

$$\begin{aligned} \int _0^{ + \infty } {\left( {\Phi _1^T{\Phi _1} - \Phi _2^T{\Phi _2}} \right) d\tau > 0} \end{aligned}$$

(B8)

Let $\Delta {c^T} = c_1^T - c_2^T$ be a positive diagonal matrix. Then

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T\Delta {c^T}\Delta c{\xi _1}d\tau }&\leqslant 2\int _0^{ + \infty } {\xi _1^T\Delta {c^T}{\Phi _1}d\tau } \nonumber \\&\leqslant 2\int _0^{ + \infty } {\sup \left( {\xi _1^T\Delta {c^T}{\Phi _1}} \right) d\tau } \end{aligned}$$

(B9)

Inequality of quadratic form leads to

$$\begin{aligned} \xi _1^T\Delta {c^T}{c_1}{\xi _1} \leqslant \lambda _{\max }^{\Delta {c^T}{c_1}}{\left\| {{\xi _1}} \right\| ^2} \end{aligned}$$

where $\lambda _{\max }^{\Delta {c^T}{c_1}}$ is the largest eigenvalue of the matrix $\Delta {c^T}{c_1}$.

It can be deduced from (B8) that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T\Delta {c^T}\Delta c{\xi _1}d\tau } \leqslant 2\int _0^{ + \infty } {\sup \left( {\xi {{_1^T}}\Delta {c^T}{\Phi _1}} \right) d\tau } \nonumber \\ \leqslant {\left\| {2\lambda _{\max }^{\Delta {c^T}{c_1}}{{\left\| {{\xi _1}} \right\| }^2}} \right\| _1} + \left\| {\xi _1^T\Delta {c^T}{\xi _2}} \right\| _1 < + \infty \end{aligned}$$

(B10)

Note that $\Delta {c^T} = c_1^T - c_2^T$ is a constant. Thus, there exists a constant ${\partial _1} > 0$ such that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _1^T{\xi _1}d\tau } \leqslant {\partial _1} < + \infty \end{aligned}$$

(B11)

A completely similar proof, one can infer that there exists a positive constant ${\partial _2}$ such that:

$$\begin{aligned} \int _0^{ + \infty } {\xi _2^T{\xi _2}d\tau } \leqslant {\partial _2} < + \infty \end{aligned}$$

(B12)

According to the convergence theory of the Barbalat integral, one can deduce that: $\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _1} = {0} ,{\text { }}\mathop {\lim }\limits _{t \rightarrow \infty } {\xi _2} = {0}$.

On the other hand, ${\alpha _1}$ and ${\alpha _2}$ are preselected coefficients (finite). Hence, from (34) it can be easily deduced that $\mathop {\lim }\limits _{t \rightarrow \infty } {S} = {0}.$

Theorem 1 has been proved.