Decentralized discrete sliding mode controller for TITO processes with time delay with experimental application

Abstract

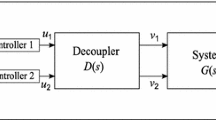
Multiple input multiple output systems posses interaction among the variables and hence are difficult to control. In addition, if these systems have slow and non-linear dynamics with time delays; it becomes more difficult to control them under the effect of parametric uncertainty. This paper presents the decentralized discrete time sliding mode controller (DSMC) for the robust tracking of two input two output (TITO) chemical processes with time delay. The ideal decoupler is used to reduce interaction among the system variables by forming decentralized structure consisting decoupled subsystems. Then for each subsystem, DSMC is independently designed and the control signal is applied to the TITO system after passing it through the decoupler. In the design procedure, an optimal sliding surface is chosen as a linear function of the system’s state error and the coefficients of sliding surface are computed by minimizing the quadratic performance index. A delay ahead predictor–corrector is used to handle system’s time delay and plant-model uncertainties. The control law is derived from the discrete time state model and sliding surface. A variable gain switching control law is proposed which results into power rate reaching law with power equal to 1. The methodology integrates ideal decoupler, optimal sliding surface and delay ahead prediction–correction; and therefore results optimal performance of the systems with less interaction. The stability condition is derived using Lyapunov approach. The stability condition results into chatter free convergent quasi sliding mode. Two benchmark simulation examples are used to demonstrate effectiveness of the proposed controller and an experimentation is performed on interacting coupled tank level control system to show its applicability to real life non-linear TITO systems.