Skip to main content

Advertisement

SpringerLink
Log in

Analysis of a two prey one predator system with disease in the first prey population

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

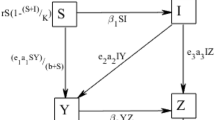
In this paper we have developed an eco-epidemic model with two prey one predator population where only first prey population is infected by an infectious disease. The interaction between first prey and predator is assumed to be governed by a Holling type II functional response where the handling time of predator for second prey is also involved. A Lotka–Volterra functional response is taken to represent the interaction between second prey and predator. Next we have studied the positivity of the solutions of the system and analyzed the existence and stability of various equilibrium points. We have introduced a time delay in the model and discussed about the stability of delayed model. It is observed that the existence of stability switches occur around the interior equilibrium. Our important mathematical findings are also numerically verified using MATLAB. Finally eco-epidemiological implications of our analytical findings are addressed critically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Holling CS (1965) The functional response of predators to prey density and its role in mimicry and population regulation. Mem Entomol Soc Can 45:3–60

    Google Scholar 

  2. Kot M (2001) Elements of mathematical ecology. Cambridge University Press, Cambridge

    Book  Google Scholar 

  3. Murray JD (1993) Mathematical biology. Springer, New York

    Book  MATH  Google Scholar 

  4. Bandyopadhyay M, Chakrabarti CG (2003) Deterministic and stochastic analysis of a non-linear prey–predator system. J Biol Syst 11:161–172

    Article  MATH  Google Scholar 

  5. Gilpin ME (1972) Enriched predator–prey systems: theoretical stability. Science 177:902–904

    Article  Google Scholar 

  6. Kuznetsov Y, Rinaldi S (1996) Remarks on food chain dynamics. Math Biosci 134:1–33

    Article  MathSciNet  MATH  Google Scholar 

  7. Li B, Kuang Y (2000) Simple food chain in a chemostat with distinct removal rates. J Math Anal Appl 242:75–92

    Article  MathSciNet  MATH  Google Scholar 

  8. Renshaw E (1995) Modelling biological population in space and time. Cambridge University Press, Cambridge

    Google Scholar 

  9. Bandyopadhyay M, Bhattacharyya R, Mukhopadhyay B (2004) Dynamics of an autotroph herbivore ecosystem with nutrient recycling. Ecol Model 176:201–209

    Article  Google Scholar 

  10. Erbe LH, Rao VSH, Freedman H (1986) Three-species food chain models with mutual interference and time delays. Math Biosci 80:57–80

    Article  MathSciNet  MATH  Google Scholar 

  11. Freedman HI, Waltman P (1977) Mathematical analysis of some three-species food chain models. Math Biosci 33:257–276

    Article  MathSciNet  MATH  Google Scholar 

  12. Freedman HI, Waltman P (1984) Persistence in a model of three interacting predator–prey populations. Math Biosci 68:213–231

    Article  MathSciNet  MATH  Google Scholar 

  13. Freedman HI, Waltman P (1985) Persistence in a model of three competitive populations. Math BIosci 73:89–101

    Article  MathSciNet  MATH  Google Scholar 

  14. Gazi NH, Khan SR, Chakrabarti CG (2009) Integration of mussel in fish-farm: mathematical model and analysis. Nonlinear Anal: Hybrid Syst 3:74–86

    MathSciNet  MATH  Google Scholar 

  15. Maiti A, Pal AK, Samanta GP (2008) Effect of time delay on a food chain model. Appl Math Comput 200:189–203

    Article  MathSciNet  MATH  Google Scholar 

  16. Ruan S (1993) A three-trophic-level model of plankton dynamics with nutrient recycling. Can Appl Math Q 1:529–553

    MATH  Google Scholar 

  17. Ruan S, Xiao D (2001) Global analysis in a predator–prey system with nonmonotonic functional response. SIAM J Appl Math 61:1445–1472

    Article  MathSciNet  MATH  Google Scholar 

  18. Sharma S, Samanta GP (2013) Dynamical behaviour of a two prey one predator system. Differ Eqn Dyn Syst 22(2):125–145. doi:10.1007/s12591-012-0158-y

  19. Srinivasu PDN, Prasad BSRV, Venkatesulu M (2007) Biological control through provision of additional food to predator: a theoretical study. Theor Popul Biol 72:111–120

    Article  MATH  Google Scholar 

  20. Takeuchi Y, Oshime Y, Matsuda H (1992) Persistence and periodic orbits of a three-competitor model with refuges. Math Biosci 108:105–125

    Article  MathSciNet  MATH  Google Scholar 

  21. Butler GJ, Freedman HI, Waltman P (1986) Uniformly persistent systems. Proc Am Math Soc 96:425–429

    Article  MathSciNet  MATH  Google Scholar 

  22. Gomez J, Zamora R (1994) Top-down effects in a tritrophic system: parasitoids enhance plant fitness. Ecology 75:1023–1030

    Article  Google Scholar 

  23. Kumar R, Freedman HI (1989) A mathematical model of facultative mutualism with populations interacting in a food chain. Math Biosci 97:235–261

    Article  MathSciNet  MATH  Google Scholar 

  24. Maiti A, Samanta GP (2005) Complex dynamics of a food chain model with mixed selection of functional responses. Bull Calcutta Math Soc 97:393–412

    MathSciNet  MATH  Google Scholar 

  25. Maiti A, Samanta GP (2006) Deterministic and stochastic analysis of a prey-dependent predator–prey system. Int J Math Educ Sci Technol 36:65–83

    Article  MathSciNet  Google Scholar 

  26. Fritzsche-Hoballah M, Turlings TCJ (2001) Experimental evidence that plants under caterpillar attack may benefit from attracting parasitoids. Evol Ecol Res 3:1–13

    Google Scholar 

  27. Grad T (1980) Persistence in food chains with general interactions. Math Biosci 51:165–174

    Article  MathSciNet  Google Scholar 

  28. Turlings TCJ, Fritzsche ME (1999) In: Chadwick DJ, Goode JA (eds) Attraction of parasitic wasp by caterpillar-damaged plants. Wiley, Chichester

  29. Van Loon J, De Boer G, Dicke M (2000) Parasitoid-plant mutualism: parasitoid attack of herbivore increases plant reproduction. Entomol Exp Appl 97:219–227

    Article  Google Scholar 

  30. Das SC, Barua KC (1990) Scope of bio-control of pests and diseases in tea plantations. In: Proceedings of the international conference tea research: global perspective Calcutta, 11–12 Jan, pp 119–125

  31. Das SC, Borthakar MC, Gope B (1989) Need for non-conventional approach in tea pest management. In: Proceedings of the 30th Tocklai conference, pp 80–89

  32. Maiti A, Pal AK, Samanta GP (2008) Usefulness of biocontrol of pests in tea: a mathematical model. Math Model Nat Phenom 3:96–113

    Article  MathSciNet  Google Scholar 

  33. Hsu SB, Hwang TW (1999) Hopf bifurcation analysis for a predator–prey system of Holling and Leslie type. Taiwan J Math 3:35–53

    MathSciNet  MATH  Google Scholar 

  34. Samanta GP, Manna D, Maiti A (2003) Bioeconomic modelling of a three-species fishery with switching effect. Korean J Comput Appl Math 12(1–2):219–231

    Article  MathSciNet  MATH  Google Scholar 

  35. Yu W, Cao J (2005) Hopf bifurcation and stability of periodic solutions for Van der Pol equation with time delay. Nonlinear Anal TMA 62:141–165

    Article  MathSciNet  MATH  Google Scholar 

  36. Beretta E, Capasso V (1986) On the general structure of epidemic systems: global asymptotic stability. Comput Math Appl 12A:677–694

    Article  MathSciNet  Google Scholar 

  37. Castillo-Chavez C, Feng Z (1998) Global stability of an age-structure model for TB and its applications to optimal vaccination strategies. Math Biosci 151:135–154

    Article  MATH  Google Scholar 

  38. Castillo-Chavez C, Song B (2004) Dynamical models of tuberculosis and their applications. Math Biosci Eng 1:361–404

    Article  MathSciNet  MATH  Google Scholar 

  39. Hethcote H (2000) The mathematics of infectious diseases. SIAM Rev 42:599–653

    Article  MathSciNet  MATH  Google Scholar 

  40. Korobeinikov A, Maini PK (2005) Nonlinear incidence and stability of infectious disease models. Math Med Biol 22:113–128

    Article  MATH  Google Scholar 

  41. Li J, Yang Y, Zhou Y (2011) Global stability of an epidemic model with latent stage and vaccination. Nonlinear Anal 12:2163–2173

    Article  MathSciNet  MATH  Google Scholar 

  42. Sharomi O, Podder CN, Gumel AB, Elbasha EH, Watmough J (2007) Role of incidence function in vaccine-induced backward bifurcation in some HIV models. Math Biosci 210:436–463

    Article  MathSciNet  MATH  Google Scholar 

  43. Venturino E (2006) On epidemics crossing the species barrier in interacting population models. Varahmihir J Math Sci 6(1):247–263

    MathSciNet  MATH  Google Scholar 

  44. Wang W (2006) Backward bifurcation of an epidemic model with treatment. Math Biosci 210:58–71

    Article  Google Scholar 

  45. Xiao D, Ruan S (2007) Global analysis of an epidemic model with nonmonotone incidence rate. Math Biosci 208:419–429

    Article  MathSciNet  MATH  Google Scholar 

  46. Xiao Y, Tang S (2010) Dynamics of infection with nonlinear incidence in a simple vaccination model. Nonlinear Anal Real World Appl 11:4154–4163

    Article  MathSciNet  MATH  Google Scholar 

  47. Chen H, Sun J (2011) Global stability of delay multigroup endemic models with group mixing and nonlinear incidence rates. Appl Math Comput 218:4391–4400

    Article  MathSciNet  MATH  Google Scholar 

  48. Enatsu Y, Messina E, Muroya Y, Nakata Y, Russo E, Vecchio A (2012) Stability analysis of delayed SIR epidemic models with a class of nonlinear incidence rates. Appl Math Comput 218:5327–5336

    Article  MathSciNet  MATH  Google Scholar 

  49. Li MY, Shu H (2012) Joint effects of mitosis and intracellular delay on viral dynamics: two parameter bifurcation analysis. J Math Biol 64:1005–1020

    Article  MathSciNet  MATH  Google Scholar 

  50. Sun C, Lin Y, Han M (2006) Stability and hopf bifurcation for an epidemic disease model with delay. Chaos, Solitons Fractals 30:204–216

    Article  MathSciNet  MATH  Google Scholar 

  51. Xue Y, Duan X (2011) Dynamic analysis of an SIR epidemic model with nonlinear incidence rate and double delays. Int J Inf Syst Sci 7:92–102

    MathSciNet  Google Scholar 

  52. Venturino E (1994) The influence of diseases on Lotka–Volterra systems. Rocky Mt J Math 24:381–402

    Article  MathSciNet  MATH  Google Scholar 

  53. Venturino E (1995) Epidemics in predator–prey models: disease in the prey. In: Arino O, Axelrod D, Kimmel M, Langlais M (eds) Mathematical population dynamics: analysis of heterogeneity, theory of epidemics, vol 1. Wuerz, Winnipeg, pp 381–393

    Google Scholar 

  54. Haque M, Venturino E (2009) Modelling disease spreading in symbiotic communities. In: Wildlife: destruction, conservation and biodiversity. Nova Science Publishers, New York

  55. Haque M (2010) A predator–prey model with disease in the pradator species only. Nonlinear Anal Real World Appl 11(010):2224–2236

    Article  MathSciNet  MATH  Google Scholar 

  56. Haque M, Greenhalgh D (2009) When predator avoids infected prey: a model based theoretical studies. IMA J Math Med Biol 27:75–94

    Article  MathSciNet  Google Scholar 

  57. Haque M, Sarwardi S, Preston S, Venturino E (2011) Effect of delay in a Lotka–Volterra type predator–prey model with a transmission disease in the predator species. Math Biosci 234(1):47–57

    Article  MathSciNet  MATH  Google Scholar 

  58. Haque M, Zhen J, Venturino E (2009) Rich dynamics of Lotka–Volterra type predator–prey model system with viral disease in prey species. Math Methods Appl Sci 32:875–898

    Article  MathSciNet  MATH  Google Scholar 

  59. Xiao YN, Chen LS (2001) Analysis of a three species eco-epidemiological model. J Math Anal Appl 258(2):733–754

    Article  MathSciNet  MATH  Google Scholar 

  60. Xiao YN, Chen LS (2001) Modelling and analysis of a predator–prey model with disease in the prey. Math Biosci 171:59–82

    Article  MathSciNet  MATH  Google Scholar 

  61. Zhou XY, Shi XY, Song XY (2009) Analysis of a delay prey–predator model with disease in the prey species only. J Korean Math Soc 46(4):713–731

    Article  MathSciNet  MATH  Google Scholar 

  62. Tewa JJ, Djeumen VY, Bowong S (2013) Predator–prey model with Holling response function of type II and SIS infectious disease. Appl Math Model 37:4825–4841

    Article  MathSciNet  Google Scholar 

  63. Hethcote H, Wang W, Han L, Ma Z (2004) A predator–prey model with infected prey. Theor Popul Biol 66:259–268

    Article  Google Scholar 

  64. Hudson PJ, Dobson AP, Newborn D (1992) Do parasites make prey more vulnerable to predation? Red grouse and parasites. J Anim Ecol 61:681–692

    Article  Google Scholar 

  65. Venturino E (2002) Epidemics in predator–prey models: disease in the predators. IMA J Math Appl Med Biol 19:185–205

    Article  MATH  Google Scholar 

  66. Anderson RM, May RM (1986) The invasion persistence and spread of infectious diseases within animal and plant communities. Philos Trans R Soc Lond B 314:533–570

    Article  Google Scholar 

  67. Hadeler KP, Freedman HI (1989) Predator–prey populations with parasitic infection. J Math Biol 27:609–631

    Article  MathSciNet  MATH  Google Scholar 

  68. Hsieh YH, Hsiao CK (2008) Predator–prey model with disease infection in both populations. Math Med Biol 25:247–266

    Article  MATH  Google Scholar 

  69. Shi XY, Cui J, Zhou XY (2011) Stability and Hopf bifurcation analysis of an eco-epidemic model with a stage structure. Nonlinear Anal 74:1088–1106

    Article  MathSciNet  MATH  Google Scholar 

  70. Zhang JF, Li WT, Yan XP (2008) Hopf bifurcation and stability of periodic solutions in a delayed eco-epidemiological system. Appl Math Comput 198:865–876

    Article  MathSciNet  MATH  Google Scholar 

  71. Zhou X, Cui J (2010) Stability and Hopf bifurcation analysis of an eco-epidemiological model with delay. J Franklin Inst 347:1654–1680

    Article  MathSciNet  MATH  Google Scholar 

  72. Li J, Gao W (2010) Analysis of predator–prey model with disease in prey. Appl Math Comput 217:4024–4035

    Article  MathSciNet  MATH  Google Scholar 

  73. Xiao Y, Chen L (2002) A ratio-dependent predator–prey model with disease in the prey. Appl Math Comput 131:397–414

    Article  MathSciNet  MATH  Google Scholar 

  74. Hale JK (1977) Theory of functional differential equations. Springer, New York

    Book  MATH  Google Scholar 

  75. Beretta E, Kuang Y (2002) Geometric stability switch criteria in delay differential systems with delay dependent parameters. SIAM J Math Anal 33:1144–1165

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The authors are very grateful to the anonymous referees and the Editor-in-Chief (Dr. Jian-Qiao Sun) for their careful reading, valuable comments and helpful suggestions, which have helped them to improve the presentation of this work significantly.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Engineering Science and Technology, Shibpur, Howrah, 711 103, India

    Swarnali Sharma & G. P. Samanta

Authors
  1. Swarnali Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. P. Samanta
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. P. Samanta.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, S., Samanta, G.P. Analysis of a two prey one predator system with disease in the first prey population. Int. J. Dynam. Control 3, 210–224 (2015). https://doi.org/10.1007/s40435-014-0107-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-014-0107-4

Keywords

Mathematics Subject Classification

Search

Navigation