Skip to main content
SpringerLink
Log in

Numerical investigation of rope-core elasticity effects on rope–sheave traction

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

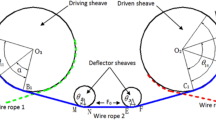
Abstract

Fiber core wire ropes are widely used in rope–sheave traction equipment such as elevators, mine hoists, and cranes due to their excellent mechanical properties and low cost. However, the mechanical behavior of the rope core and its influence on the traction performance have not been thoroughly investigated. Therefore, this study aims to examine how the elasticity of the rope core affects the traction performance of wire ropes. A finite element model of a wire rope wrapped on a sheave was developed and validated by high-speed camera experiments. The results indicated that the core elasticity increased the stress in the outer wires, resulting in a reduction in the rope strength. According to the boundary conditions of our finite element model, a specific solution to a system of ordinary differential equations describing the tangential contact force at the traction interface is given. This particular solution reveals the tendency of the core elasticity to enhance the rope–sheave slip by increasing the tangential contact force. By monitoring the rope tension, the study discovered a correlation between rope–sheave traction and rope’s interwire friction, which has not been reported before. These findings enhance our understanding of the influence of rope core elasticity on traction and highlight the importance of considering the core elasticity in wire rope design.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

\({T}_{1}\) :

Tension at the tight end of the rope

\({T}_{2}\) :

Tension at the loose end of the rope

\(f\) :

The equivalent coefficient of friction (COF) between rope and sheave

\(\theta\) :

The wrap angle between the rod and cylinder

\({E}_{1}\) :

Elastic modulus of the outer wires inside the rope

\({E}_{2}\) :

Elastic modulus of the core wire inside the rope

\({E}_{2}\) :

Elastic modulus of the traction sheave

\({E}^{*}\) :

Equivalent elastic modulus of the rope

\(\nu\) :

Poisson's ratio

\(\rho\) :

The density of the materials (g/cm3)

\({\mu }_{{\text{sw}}}\) :

COF between rope and sheave

\({\mu }_{{\text{wc}}}\) :

COF between the core wire and the outer wires inside the rope

\({\mu }_{{\text{ww}}}\) :

COF between the adjacent outer wires inside the rope

\({U}_{i}\) :

Translational displacement along \(x,y\) or \(z\)-axis

\({{{UR}}}_{i}\) :

Angular displacement along \(x,y\) or \(z\)-axis

\({{{VR}}}_{i}\) :

Angular velocity along \(x,y\) or \(z\)-axis

\({F}_{i}\) :

Force along \(x,y\) or \(z\)-axis

\({M}_{i}\) :

Torque along \(x,y\) or \(z\)-axis

\(Q\) :

Critic tension ratio

\(\alpha\) :

Winding angle

\(\tau (\alpha )\) :

Tangential contact stress between rope and sheave

\({k}_{{\text{s}}}\) :

Stiffness of a bristle

\(s(\alpha )\) :

Bristle deformation

\({T}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}(\alpha )\) :

The second derivative of the rope tension with respect to the winding angle

\(R\) :

Radius of the traction sheave

\({v}_{1}\) :

Velocity of the rope

\(\omega\) :

Angular velocity of the sheave

\({E}^{*}\) :

Equivalent elastic modulus of the rope

\(A\) :

Equivalent cross-sectional area of the rope

\(N(\alpha )\) :

Normal contact force between rope and sheave

\({f}_{{\text{wc}}}\) :

Friction force between the rope core and the outer wires

\({L}_{{\text{w}}}\) :

Length of the outer wires at the loose end

\({L}_{{\text{c}}}\) :

Length of the rope core at the loose end

References

  1. Eytelwein JA (1793) Ausgaben großtentheils aus der angewandten mathematik. Freidrich Manrer, Berlin

    Google Scholar 

  2. Jung JH, Pan N, Kang TJ (2008) Capstan equation including bending rigidity and non-linear frictional behavior. Mech Mach Theory 43:661–675. https://doi.org/10.1016/j.mechmachtheory.2007.06.002

    Article  Google Scholar 

  3. Jung JH, Pan N, Kang TJ (2008) Generalized capstan problem: Bending rigidity, nonlinear friction, and extensibility effect. Tribol Int 41:524–534. https://doi.org/10.1016/j.triboint.2007.11.005

    Article  CAS  Google Scholar 

  4. Lu Y, Fan D, Liu H, Hei M (2015) Transmission capability of precise cable drive including bending rigidity. Mech Mach Theory 94:132–140. https://doi.org/10.1016/j.mechmachtheory.2015.07.004

    Article  Google Scholar 

  5. Grandgeorge P, Sano TG, Reis PM (2022) An elastic rod in frictional contact with a rigid cylinder. J Mech Phys Solids 164:104885. https://doi.org/10.1016/j.jmps.2022.104885

    Article  MathSciNet  CAS  Google Scholar 

  6. Frendo F, Bucchi F (2020) “Brush model” for the analysis of flat belt transmissions in steady-state conditions. Mech Mach Theory 143:103653. https://doi.org/10.1016/j.mechmachtheory.2019.103653

    Article  Google Scholar 

  7. Frendo F, Bucchi F (2020) Enhanced brush model for the mechanics of power transmission in flat belt drives under steady–state conditions: effect of belt elasticity. Mech Mach Theory 153:103998. https://doi.org/10.1016/j.mechmachtheory.2020.103998

    Article  Google Scholar 

  8. Bucchi F, Frendo F (2021) Analysis of belt transmissions capabilities using the brush model. IOP Conf Ser: Mater Sci Eng 1038:012076. https://doi.org/10.1088/1757-899X/1038/1/012076

    Article  Google Scholar 

  9. Chen Y, Meng F, Gong X (2017) Full contact analysis of wire rope strand subjected to varying loads based on semi-analytical method. Int J Solids Struct 117:51–66. https://doi.org/10.1016/j.ijsolstr.2017.04.004

    Article  Google Scholar 

  10. Costello GA (1997) Theory of wire rope. Springer, New York, New York, NY

    Book  Google Scholar 

  11. Liu L, Liu D, Wu X, He Y (2021) Optimal structural patterns of multi-strand wire ropes. Int J Solids Struct 225:111070. https://doi.org/10.1016/j.ijsolstr.2021.111070

    Article  Google Scholar 

  12. Usabiaga H, Pagalday JM (2008) Analytical procedure for modelling recursively and wire by wire stranded ropes subjected to traction and torsion loads. Int J Solids Struct 45:5503–5520. https://doi.org/10.1016/j.ijsolstr.2008.04.009

    Article  Google Scholar 

  13. Utting WS, Jones N (1987) The response of wire rope strands to axial tensile loads—part I. Experimental results and theoretical predictions. Int J Mech Sci 29:605–619. https://doi.org/10.1016/0020-7403(87)90033-6

    Article  Google Scholar 

  14. Li X, Liang L, Wu S (2018) Analysis of mechanical behaviors of internal helically wound strand wires of stranded wire helical spring. Proc Inst Mech Eng C J Mech Eng Sci 232:1009–1019. https://doi.org/10.1177/0954406217696517

    Article  Google Scholar 

  15. Vu TD, Durville D, Davies P (2015) Finite element simulation of the mechanical behavior of synthetic braided ropes and validation on a tensile test. Int J Solids Struct 58:106–116. https://doi.org/10.1016/j.ijsolstr.2014.12.022

    Article  Google Scholar 

  16. Fontanari V, Benedetti M, Monelli BD (2015) Elasto-plastic behavior of a Warrington-Seale rope: experimental analysis and finite element modeling. Eng Struct 82:113–120. https://doi.org/10.1016/j.engstruct.2014.10.032

    Article  Google Scholar 

  17. Stanova E, Fedorko G, Kmet S et al (2015) Finite element analysis of spiral strands with different shapes subjected to axial loads. Adv Eng Softw 83:45–58. https://doi.org/10.1016/j.advengsoft.2015.01.004

    Article  Google Scholar 

  18. Nawrocki A, Labrosse M (2000) A finite element model for simple straight wire rope strands. Comput Struct 77:345–359. https://doi.org/10.1016/S0045-7949(00)00026-2

    Article  Google Scholar 

  19. Meier C, Grill MJ, Wall WA, Popp A (2018) Geometrically exact beam elements and smooth contact schemes for the modeling of fiber-based materials and structures. Int J Solids Struct 154:124–146. https://doi.org/10.1016/j.ijsolstr.2017.07.020

    Article  Google Scholar 

  20. Ma J, Guo Y (2019) Stress analysis of steel wire in strand based on optical lever principle and finite element calculation. J Braz Soc Mech Sci Eng 42:37. https://doi.org/10.1007/s40430-019-2120-1

    Article  CAS  Google Scholar 

  21. Zhang W, Yuan X, Chen C, Yang L (2021) Finite element analysis of steel wire ropes considering creep and analysis of influencing factors of creep. Eng Struct 229:111665. https://doi.org/10.1016/j.engstruct.2020.111665

    Article  Google Scholar 

  22. Chen Y, Meng F, Gong X (2016) Interwire wear and its influence on contact behavior of wire rope strand subjected to cyclic bending load. Wear 368–369:470–484. https://doi.org/10.1016/j.wear.2016.10.020

    Article  CAS  Google Scholar 

  23. Cao X, Wu W (2018) The establishment of a mechanics model of multi-strand wire rope subjected to bending load with finite element simulation and experimental verification. Int J Mech Sci 142–143:289–303. https://doi.org/10.1016/j.ijmecsci.2018.04.051

    Article  Google Scholar 

  24. Zhang D, Ostoja-Starzewski M (2016) finite element solutions to the bending stiffness of a single-layered helically wound cable with internal friction. J Appl Mech 83:031003. https://doi.org/10.1115/1.4032023

    Article  Google Scholar 

  25. Wang D, Zhang D, Wang S, Ge S (2013) Finite element analysis of hoisting rope and fretting wear evolution and fatigue life estimation of steel wires. Eng Fail Anal 27:173–193. https://doi.org/10.1016/j.engfailanal.2012.08.014

    Article  Google Scholar 

  26. Chang X, Peng Y, Zhu Z et al (2019) Breaking failure analysis and finite element simulation of wear-out winding hoist wire rope. Eng Fail Anal 95:1–17. https://doi.org/10.1016/j.engfailanal.2018.08.027

    Article  Google Scholar 

  27. Zhou P, Zhou G, Han L et al (2023) Failure analysis for hoisting wire ropes with local accumulated broken wire damage on the surface. J Mech Sci Technol. https://doi.org/10.1007/s12206-023-0611-6

    Article  Google Scholar 

  28. Shi X, Pan Y, Ma X (2017) Modeling and analysis of the rope-sheave interaction at traction interface. J Appl Mech 10(1115/1):4035584

    Google Scholar 

  29. Ma X, Pan Y, Shi X (2018) Experimental investigation of friction and slip at the traction interface of rope and sheave. J Appl Mech 85(1):011006

    Article  Google Scholar 

  30. Zhang J, Wang D, Zhang D et al (2018) Dynamic contact and slip characteristics of bent hoisting rope in coal mine. J Braz Soc Mech Sci Eng 40:120. https://doi.org/10.1007/s40430-018-1044-5

    Article  ADS  Google Scholar 

  31. Wang D, Araújo JA (2019) Tribo-fatigue behaviors of steel wire rope under bending fatigue with the variable tension. Wear 428–429:154–161. https://doi.org/10.1016/j.wear.2019.03.004

    Article  CAS  Google Scholar 

  32. Qin Z, Huang Q, Jin H, Xue H (2020) Multi-body dynamics simulation of hoisting wire rope and its stress analysis. JNWPU 38:485–493. https://doi.org/10.1051/jnwpu/20203830485

    Article  Google Scholar 

  33. Liu J, Zhao Z, Zhang X et al (2023) Superelasticity SMA cables and its simplified FE model. J Braz Soc Mech Sci Eng 45:163. https://doi.org/10.1007/s40430-022-03957-2

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledged the support of National Natural Science Foundation of China under Grant No. 519350

Author information

Authors and Affiliations

  1. State Key Laboratory of Mechanical System and Vibration, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, People’s Republic of China

    Yunting Han, Gang Zhang, Songtao Hu & Xi Shi

  2. Shanghai Institute of Aerospace System Engineering, Shanghai, 201108, People’s Republic of China

    Xiaolong Ma

Authors
  1. Yunting Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiaolong Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Songtao Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xi Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Songtao Hu or Xi Shi.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Technical Editor: João Marciano Laredo dos Reis.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Han, Y., Ma, X., Zhang, G. et al. Numerical investigation of rope-core elasticity effects on rope–sheave traction. J Braz. Soc. Mech. Sci. Eng. 46, 90 (2024). https://doi.org/10.1007/s40430-023-04673-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-023-04673-1

Keywords

Search

Navigation