Skip to main content
SpringerLink
Log in

A smeared stiffener model for vibration analysis of anisogrid-stiffened composite conical shells using differential quadrature method

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

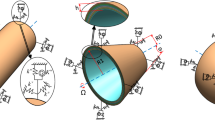
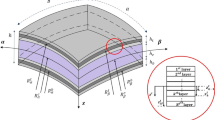
Abstract

Anisogrid-stiffened composite conical shells have been widely applied in aerospace engineering as highly efficient structural elements. In this paper, the smeared stiffener approach is adopted to analyze the free vibration behavior of stiffened composite conical shells. The stiffening elements are modeled as beams that can bear bending moments and shear forces along with the axial forces. The stiffeners' stiffness is superimposed onto those of the shell, resulting in a variable equivalent stiffness for the entire structure. According to the Donnell-type shell model and Hamilton’s law, the kinetic and elastic energies are formulated, and then, the coupled partial differential equations of the anisogrid-stiffened composite conical shells are derived. Using the differential quadrature method (DQM) and appropriate harmonic functions, the equations are numerically solved in meridional and circumferential directions. Validation of the results is accomplished by making a comparison between the obtained results and those of other studies. Finally, several of the essential design variables are analyzed mathematically for various boundary conditions, and conclusions are drawn based on these findings. It is found that the influence of the boundary condition at the small end of the conical shell on the natural frequency of the anisogrid-stiffened structure is greater compared to the un-stiffened structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Vasiliev V, Barynin V, Rasin A (2001) Anisogrid lattice structures–survey of development and application. Compos Struct 54(2–3):361–370. https://doi.org/10.1016/S0263-8223(01)00111-8

    Article  Google Scholar 

  2. Vasiliev V, Razin A (2006) Anisogrid composite lattice structures for spacecraft and aircraft applications. Compos Struct 76(1–2):182–189. https://doi.org/10.1016/j.compstruct.2006.06.025

    Article  Google Scholar 

  3. Vasiliev V, Razin A, Totaro G, De Nicola F (2005) Anisogrid conical adapters for commercial space application. AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies Conference.

  4. Vasiliev VV, Barynin VA, Razin AF (2012) Anisogrid composite lattice structures–Development and aerospace applications. Compos Struct 94(3):1117–1127. https://doi.org/10.1016/j.compstruct.2011.10.023

    Article  Google Scholar 

  5. Totaro G (2016) Flexural, torsional, and axial global stiffness properties of anisogrid lattice conical shells in composite material. Compos Struct 153:738–745. https://doi.org/10.1016/j.compstruct.2016.06.072

    Article  Google Scholar 

  6. Ghahfarokhi DS, Rahimi G (2018) An analytical approach for global buckling of composite sandwich cylindrical shells with lattice cores. Int J Solids Struct 146:69–79. https://doi.org/10.1016/j.ijsolstr.2018.03.021

    Article  Google Scholar 

  7. Liu R, Zhong Y, Shi Z, Liu X, Chen J (2022) Free and forced vibration analysis of pyramid lattice sandwich plate based on the dimensional reduction model. Thin-Walled Struct 174:109155. https://doi.org/10.1016/j.tws.2022.109155

    Article  Google Scholar 

  8. Zarei M, Rahimi G (2022) Effect of boundary condition and variable shell thickness on the vibration behavior of grid-stiffened composite conical shells. Appl Acoust 188:108546. https://doi.org/10.1016/j.apacoust.2021.108546

    Article  Google Scholar 

  9. Zarei M, Rahimi G (2022) Buckling resistance of joined composite sandwich conical–cylindrical​ shells with lattice core under lateral pressure. Thin-Walled Struct 174:109027. https://doi.org/10.1016/j.tws.2022.109027

    Article  Google Scholar 

  10. Lopatin A, Morozov E, Shatov A (2021) Buckling of biaxially compressed anisogrid stiffened composite cylindrical panel with clamped edges. Eur J Mech-A/Solids 85:104090. https://doi.org/10.1016/j.euromechsol.2020.104090

    Article  MathSciNet  Google Scholar 

  11. Liang K, Yang C, Sun Q (2020) A smeared stiffener based reduced-order modelling method for buckling analysis of isogrid-stiffened cylinder. Appl Math Model 77:756–772. https://doi.org/10.1016/j.apm.2019.07.061

    Article  MathSciNet  Google Scholar 

  12. Belardi VG, Fanelli P, Vivio F (2018) Design, analysis and optimization of anisogrid composite lattice conical shells. Compos B Eng 150:184–195. https://doi.org/10.1016/j.compositesb.2018.05.036

    Article  Google Scholar 

  13. Ren M, Li T, Huang Q, Wang B (2014) Numerical investigation into the buckling behavior of advanced grid stiffened composite cylindrical shell. J Reinf Plast Compos 33(16):1508–1519. https://doi.org/10.1177/0731684414537881

    Article  Google Scholar 

  14. Xu Y, Tong Y, Liu M, Suman B (2016) A new effective smeared stiffener method for global buckling analysis of grid stiffened composite panels. Compos Struct 158:83–91. https://doi.org/10.1016/j.compstruct.2016.09.015

    Article  Google Scholar 

  15. Wodesenbet E, Kidane S, Pang S-S (2003) Optimization for buckling loads of grid stiffened composite panels. Compos Struct 60(2):159–169. https://doi.org/10.1016/S0263-8223(02)00315-X

    Article  Google Scholar 

  16. Rikards R, Chate A, Ozolinsh O (2001) Analysis for buckling and vibrations of composite stiffened shells and plates. Compos Struct 51(4):361–370. https://doi.org/10.1016/S0263-8223(00)00151-3

    Article  Google Scholar 

  17. Hao P, Wang B, Li G, Meng Z, Wang L (2015) Hybrid framework for reliability-based design optimization of imperfect stiffened shells. AIAA J 53(10):2878–2889. https://doi.org/10.2514/1.J053816

    Article  Google Scholar 

  18. Wang B, Tian K, Zhou C, Hao P, Zheng Y, Ma Y, Wang J (2017) Grid-pattern optimization framework of novel hierarchical stiffened shells allowing for imperfection sensitivity. Aerosp Sci Technol 62:114–121. https://doi.org/10.1016/j.ast.2016.12.002

    Article  Google Scholar 

  19. Wang D, Abdalla MM (2015) Global and local buckling analysis of grid-stiffened composite panels. Compos Struct 119:767–776. https://doi.org/10.1016/j.compstruct.2014.09.050

    Article  Google Scholar 

  20. Reddy AD, Valisetty RR, Rehfield LW (1985) Continuous filament wound composite concepts for aircraft fuselage structures. J Aircr 22(3):249–255. https://doi.org/10.2514/3.45115

    Article  Google Scholar 

  21. Szilard R (2004) Theories and applications of plate analysis: classical, numerical and engineering methods. Appl Mech Rev 57(6):B32–B33

    Article  Google Scholar 

  22. Troitsky MS (1976) Stiffened plates: bending, stability, and vibrations: Elsevier Scientific Publishing Company

  23. Kidane S, Li G, Helms J, Pang S-S, Woldesenbet E (2003) Buckling load analysis of grid stiffened composite cylinders. Compos B Eng 34(1):1–9. https://doi.org/10.1016/S1359-8368(02)00074-4

    Article  Google Scholar 

  24. Zhang Y, Xue Z, Chen L, Fang D (2009) Deformation and failure mechanisms of lattice cylindrical shells under axial loading. Int J Mech Sci 51(3):213–221. https://doi.org/10.1016/j.ijmecsci.2009.01.006

    Article  Google Scholar 

  25. Zarei M, Rahimi G, Hemmatnezhad M (2020) Free vibrational characteristics of grid-stiffened truncated composite conical shells. Aerosp Sci Technol 99:105717. https://doi.org/10.1016/j.ast.2020.105717

    Article  Google Scholar 

  26. Shi H, Fan H, Shao G (2023) Dynamic theory of composite anisogrid lattice conical shells with nonconstant stiffness and density. Appl Math Model 115:661–690. https://doi.org/10.1016/j.apm.2022.11.019

    Article  MathSciNet  Google Scholar 

  27. Banijamali SM, Jafari AA (2021) Free vibration analysis of rotating functionally graded conical shells reinforced by anisogrid lattice structure. Mech Based Des Struct Mach. https://doi.org/10.1080/15397734.2021.1881539

    Article  Google Scholar 

  28. Naderi AA (2023) Vibrational behavior investigation of composite conical shells reinforced by an anisogrid lattice structure using differential quadrature method. Aerosp Knowl Technol J 12(1):183–202

    Google Scholar 

  29. Morozov E, Lopatin A, Nesterov V (2011) Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells. Compos Struct 93(2):308–323. https://doi.org/10.1016/j.compstruct.2010.09.014

    Article  Google Scholar 

  30. Fan H, Jin F, Fang D (2009) Uniaxial local buckling strength of periodic lattice composites. Mater Des 30(10):4136–4145. https://doi.org/10.1016/j.matdes.2009.04.034

    Article  Google Scholar 

  31. Hou A, Gramoll K (1998) Compressive strength of composite lattice structures. J Reinf Plast Compos 17(5):462–483. https://doi.org/10.1177/073168449801700505

    Article  Google Scholar 

  32. Frulloni E, Kenny J, Conti P, Torre L (2007) Experimental study and finite element analysis of the elastic instability of composite lattice structures for aeronautic applications. Compos Struct 78(4):519–528. https://doi.org/10.1016/j.compstruct.2005.11.013

    Article  Google Scholar 

  33. Vasiliev V, Lopatin A (1992) Theory of lattice and stiffened composite shells. Mechanics of composite materials, edited by Tarnopolskii YM(in Russian) Riga: Zinatne 82–8

  34. Xiang X, Guoyong J, Wanyou L, Zhigang L (2014) A numerical solution for vibration analysis of composite laminated conical, cylindrical shell and annular plate structures. Compos Struct 111:20–30. https://doi.org/10.1016/j.compstruct.2013.12.019

    Article  Google Scholar 

  35. Liew KM, Ng TY, Zhao X (2005) Free vibration analysis of conical shells via the element-free kp-Ritz method. J Sound Vib 281(3–5):627–645. https://doi.org/10.1016/j.jsv.2004.01.005

    Article  Google Scholar 

  36. Irie T, Yamada G, Kaneko Y (1982) Free vibration of a conical shell with variable thickness. J Sound Vib 82(1):83–94. https://doi.org/10.1016/0022-460X(82)90544-2

    Article  Google Scholar 

  37. Viswanathan K, Javed S, Prabakar K, Aziz Z, Bakar IA (2015) Free vibration of anti-symmetric angle-ply laminated conical shells. Compos Struct 122:488–495. https://doi.org/10.1016/j.compstruct.2014.11.075

    Article  Google Scholar 

  38. Shu C (1996) Free vibration analysis of composite laminated conical shells by generalized differential quadrature. J Sound Vib 194(4):587–604. https://doi.org/10.1006/jsvi.1996.0379

    Article  Google Scholar 

  39. Bellman R, Kashef B, Casti J (1972) Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations. J Comput Phys 10(1):40–52. https://doi.org/10.1016/0021-9991(72)90089-7

    Article  MathSciNet  Google Scholar 

  40. Bert CW, Malik M (1996). Differential quadrature method in computational mechanics: a review. https://doi.org/10.1115/1.3101882

    Article  Google Scholar 

  41. Eftekhari S (2016) Differential quadrature procedure for in-plane vibration analysis of variable thickness circular arches traversed by a moving point load. Appl Math Model 40(7–8):4640–4663. https://doi.org/10.1016/j.apm.2015.11.046

    Article  MathSciNet  Google Scholar 

  42. Ersoy H, Mercan K, Civalek Ö (2018) Frequencies of FGM shells and annular plates by the methods of discrete singular convolution and differential quadrature methods. Compos Struct 183:7–20. https://doi.org/10.1016/j.compstruct.2016.11.051

    Article  Google Scholar 

  43. Hao Y, Li H, Zhang W, Ge X, Yang S, Cao Y (2022) Active vibration control of smart porous conical shell with elastic boundary under impact loadings using GDQM and IQM. Thin-Walled Struct 175:109232. https://doi.org/10.1016/j.tws.2022.109232

    Article  Google Scholar 

  44. Tornabene F (2016) General higher-order layer-wise theory for free vibrations of doubly-curved laminated composite shells and panels. Mech Adv Mater Struct 23(9):1046–1067. https://doi.org/10.1080/15376494.2015.1121522

    Article  MathSciNet  Google Scholar 

  45. Kamarian S, Salim M, Dimitri R, Tornabene F (2016) Free vibration analysis of conical shells reinforced with agglomerated carbon nanotubes. Int J Mech Sci 108:157–165. https://doi.org/10.1016/j.ijmecsci.2016.02.006

    Article  Google Scholar 

  46. Roy S, Thakur SN, Ray C (2021) Free vibration analysis of laminated composite hybrid and GFRP shells based on higher order zigzag theory with experimental validation. Eur J Mech A/Solids 88:104261. https://doi.org/10.1016/j.euromechsol.2021.104261

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Flight & Engineering Department, Imam Ali University, Tehran, Iran

    Ali Asghar Naderi, Hussein Pachdaman & Alireza Zandieh

Authors
  1. Ali Asghar Naderi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hussein Pachdaman
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alireza Zandieh
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

AAN and HP involved in simulation and figure preparation; AAN and HP involved in extraction of the formulations/relations; AAN contributed to conceptualization; AAN and AZ involved in writing and editing; AAN and AZ involved in supervision; and AAN involved in project administration. All authors have read and agreed to the final version of the manuscript.

Corresponding author

Correspondence to Ali Asghar Naderi.

Ethics declarations

Conflict of interest

The authors confirm that there is no conflict of interest with any educational and financial organizations regarding the content of this paper.

Additional information

Technical Editor: Aurelio Araujo.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

In Eq. (39), Elements \({\Gamma }_{11}-{\Gamma }_{55}\) are related with the conditions at \(x={x}_{0}\), which are defined as:

Clamped (C):

$$\begin{gathered} \Gamma_{11} = \Gamma_{22} = \Gamma_{33} = \Gamma_{44} = \Gamma_{55} = I_{1} , \hfill \\ \Gamma_{12} = \Gamma_{13} = \Gamma_{14} = \Gamma_{15} = \Gamma_{21} = \Gamma_{23} = \Gamma_{24} = \Gamma_{25} = \Gamma_{31} = \Gamma_{32} = \Gamma_{34} = \Gamma_{35} = \Gamma_{41} = \Gamma_{42} = \Gamma_{43} \hfill \\ = \Gamma_{45} = \Gamma_{51} = \Gamma_{52} = \Gamma_{53} = \Gamma_{54} = \left\{ 0 \right\}_{1 \times N} , \hfill \\ \end{gathered}$$
(45)

Simply supported (S):

$$\begin{gathered} \Gamma_{11} = A_{11,11} A_{1} + A_{12,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\,\Gamma_{14} = \Gamma_{41} = B_{11,11} A_{1} + B_{12,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\, \hfill \\ \Gamma_{44} = D_{11,11} A_{1} + D_{12,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Gamma_{22} = \Gamma_{33} = \Gamma_{55} = I_{1} ,\,\,\,\,\,\,\,\,\,\,\Gamma_{12} = \Gamma_{13} = \Gamma_{15} = \Gamma_{21} = \Gamma_{23} \hfill \\ = \Gamma_{24} = \Gamma_{25} = \Gamma_{31} = \Gamma_{32} = \Gamma_{34} = \Gamma_{35} = \Gamma_{42} = \Gamma_{43} = \Gamma_{45} = \Gamma_{51} = \Gamma_{52} = \Gamma_{53} = \Gamma_{54} = \left\{ 0 \right\}_{1 \times N} , \hfill \\ \end{gathered}$$
(46)

Free (F):

$$\begin{aligned} \Gamma_{11} = & A_{11,11} A_{1} + A_{12,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\,\Gamma_{12} = nA_{12,11} a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{13} = A_{12,11} \cos \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{14} = B_{11,11} A_{1} + B_{12,11} \sin \alpha \,a_{1,1} , \\ \Gamma_{15} = & nB_{12,11} a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{21} = - nA_{66,11} a_{1,1} ,\,\,\,\,\,\,\,\,\Gamma_{22} = A_{66,11} A_{1} - A_{66,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\Gamma_{23} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\,\Gamma_{24} = - nB_{66,11} a_{1,1} \\ \Gamma_{25} = & B_{66,11} A_{1} - B_{66,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{31} = \Gamma_{32} = \Gamma_{35} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\,\,\,\Gamma_{33} = A_{1} ,\,\,\,\,\,\,\Gamma_{34} = I_{1} ,\,\,\,\,\,\,\,\,\Gamma_{41} = B_{11,11} A_{1} + B_{12,11} \sin \alpha \,a_{1,1} , \\ \Gamma_{42} = & nB_{12,11} a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{43} = B_{12,11} \cos \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\Gamma_{44} = D_{11,11} A_{1} + D_{12,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\,\,\,\Gamma_{45} = nD_{12,11} \,a_{1,1} , \\ \Gamma_{51} = & - nB_{66,11} a_{1,1} ,\,\,\,\,\Gamma_{52} = B_{66,11} A_{1} - B_{66,11} \sin \alpha \,a_{1,1} ,\,\,\,\,\,\Gamma_{53} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\Gamma_{54} = - nD_{66,11} \,a_{1,1} ,\,\,\,\,\,\Gamma_{55} = D_{66,11} A_{1} - D_{66,11} \sin \alpha \,a_{1,1} , \\ \end{aligned}$$
(47)

And elements \({\Gamma }_{61}-{\Gamma }_{105}\) are related with the conditions at \(x={x}_{0}+L\), which are defined as:

Clamped (C):

$$\begin{gathered} \Gamma_{61} = \Gamma_{72} = \Gamma_{83} = \Gamma_{94} = \Gamma_{105} = I_{N} , \hfill \\ \Gamma_{62} = \Gamma_{63} = \Gamma_{64} = \Gamma_{65} = \Gamma_{71} = \Gamma_{73} = \Gamma_{74} = \Gamma_{75} = \Gamma_{81} = \Gamma_{82} = \Gamma_{84} = \Gamma_{85} = \Gamma_{91} = \Gamma_{92} = \Gamma_{93} \hfill \\ = \Gamma_{95} = \Gamma_{101} = \Gamma_{102} = \Gamma_{103} = \Gamma_{104} = \left\{ 0 \right\}_{1 \times N} , \hfill \\ \end{gathered}$$
(48)

Simply supported (S):

$$\begin{gathered} \Gamma_{61} = A_{11,NN} A_{N} + A_{12,N} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\,\Gamma_{64} = \Gamma_{91} = B_{11,NN} A_{N} + B_{12,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\, \hfill \\ \Gamma_{94} = D_{11,NN} A_{N} + D_{12,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Gamma_{72} = \Gamma_{83} = \Gamma_{105} = I_{1} ,\,\,\,\,\,\,\,\,\,\Gamma_{62} = \Gamma_{63} = \Gamma_{65} = \Gamma_{71} = \Gamma_{73} \hfill \\ = \Gamma_{74} = \Gamma_{75} = \Gamma_{81} = \Gamma_{82} = \Gamma_{84} = \Gamma_{85} = \Gamma_{92} = \Gamma_{93} = \Gamma_{95} = \Gamma_{101} = \Gamma_{102} = \Gamma_{103} = \Gamma_{104} = \left\{ 0 \right\}_{1 \times N} , \hfill \\ \end{gathered}$$
(49)

Free (F):

$$\begin{gathered} \Gamma_{61} = A_{11,NN} A_{N} + A_{12,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\,\Gamma_{62} = nA_{12,NN} a_{1,N} ,\,\,\,\,\,\,\,\Gamma_{63} = A_{12,NN} \cos \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\Gamma_{64} = B_{11,NN} A_{N} + B_{12,NN} \sin \alpha \,a_{1,N} , \hfill \\ \Gamma_{65} = nB_{12,NN} a_{1,N} ,\,\,\,\,\,\,\,\Gamma_{71} = - nA_{66,NN} a_{1,N} ,\,\,\,\,\,\,\,\,\Gamma_{72} = A_{66,NN} A_{N} - A_{66,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\Gamma_{73} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\,\Gamma_{74} = - nB_{66,NN} a_{1,N} \hfill \\ \Gamma_{75} = B_{66,NN} A_{N} - B_{66,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\Gamma_{81} = \Gamma_{82} = \Gamma_{85} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\Gamma_{83} = A_{1} ,\,\,\,\,\,\Gamma_{84} = I_{1} ,\,\,\,\,\,\Gamma_{91} = B_{11,NN} A_{N} + B_{12,NN} \sin \alpha \,a_{1,N} , \hfill \\ \Gamma_{92} = nB_{12,NN} a_{1,N} ,\,\,\,\,\,\Gamma_{93} = B_{12,NN} \cos \alpha \,a_{1,N} ,\,\,\,\,\Gamma_{94} = D_{11,11} A_{N} + D_{12,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\Gamma_{95} = nD_{12,NN} \,a_{1,N} ,\,\,\,\,\Gamma_{101} = - nB_{66,NN} a_{1,N} ,\, \hfill \\ \Gamma_{102} = B_{66,NN} A_{N} - B_{66,NN} \sin \alpha \,a_{1,N} ,\,\,\,\,\,\,\,\,\Gamma_{103} = \left\{ 0 \right\}_{1 \times N} ,\,\,\,\,\,\,\,\Gamma_{104} = - nD_{66,NN} \,a_{1,N} ,\,\,\,\,\,\,\Gamma_{105} = D_{66,NN} A_{N} - D_{66,NN} \sin \alpha \,a_{1,N} , \hfill \\ \end{gathered}$$
(50)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Naderi, A.A., Pachdaman, H. & Zandieh, A. A smeared stiffener model for vibration analysis of anisogrid-stiffened composite conical shells using differential quadrature method. J Braz. Soc. Mech. Sci. Eng. 46, 38 (2024). https://doi.org/10.1007/s40430-023-04606-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-023-04606-y

Keywords

Search

Navigation