1 Introduction

As compared to active magnetic bearings [1], in permanent magnet bearings (PMB) [2], the rotor levitation is achieved with permanent magnets alone and doesn’t require any external energy source and feedback system. Permanent magnet bearings improved the overall system efficiency and have replaced conventional bearings in various applications [3,4,5,6]. Using Amperian and Coulombian models, researchers have provided analytical equations of force and stiffness for single ring pair [7,8,9,10,11,12] and multi-ring PMB [13,14,15,16,17]. Further to improve the bearing characteristics, the optimization [18,19,20,21] of PMB has been reported by many authors in the recent past. The active [22] or passive dampers can improve the poor damping property of PMB. The active damper uses sensors and external energy source devices, while passive dampers, like eddy current and viscoelastic type [23], don’t require any external source device and sensors. Among these, an eddy current damper (ECD) is the best suitable damper that can be used to enhance the damping characteristics of PMB. In [24], the authors included a copper plate on the surface of the rotor to develop an ECD in a single-layer PMB and developed damping force and coefficients equations. The results of equations showed a higher variation from experimental results. For a turbo-compressor rotor, Fang et al. [25] presented an ECD for a PMB and presented an analytical model. An optimum design approach was used to improve the damping coefficient and maximizing axial stiffness. Detoni et al. [26] proposed an analytical method for determining ECD properties for rotors supported by PMB. The proposed analytical model was utilized in conjunction with the FEA curve fitting findings to evaluate the mechanical impedance characteristics. Our previous efforts presented a detailed methodology for designing optimized MRPMB [27, 28] for three parameters (air gap, length, and diameter of a bearing). Till now, the eddy current damping system for an optimized MRPMB was not analyzed by the researchers. The authors’ work [29, 30] also shows that force and stiffness associated with axially magnetized MRPMB can be enhanced by providing an axial air gap between ring magnets of a rotor. It was also shown that there is an optimum value of an axial air gap at which bearing characteristics are maximum compared to bearings without an axial air gap. In our previous work [31], NECDS for an optimized multi-layer thrust PMB was proposed, and analysis results were presented. In this paper, the conventional and novel eddy current damping systems are discussed in Sect. 2. The MRPMB is designed and optimized based on three general parameters for maximum radial force and stiffness in Sect. 3. Then, the radial, axial, and rotational damping forces and coefficients are evaluated by analyzing CECDS for MRPMB in Sect. 4. Further, the copper plate thickness is optimized for maximum damping forces. Finally, in Sect. 5, copper rings are provided between the axially stacked magnet rings on the rotor to form NECDS for an optimized MRPMB and the analysis of NECDS is carried out for axial, radial, and rotational damping forces and coefficients.

2 Conventional and novel Eddy current dampers

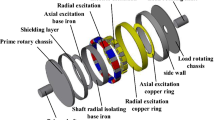
In MRPMB, the levitation of rotor rings happens due to the magnetic force interactions between the faces of magnets. Figure 1a shows the bearing setup of single ring pair, in which one ring is attached on the rotor and another on the stator, and both are magnetized (axially) in the same direction. The properties of mono-layer bearings are low, and to maximize properties, and permanent magnet rings are provided on the stator and the rotor to form multi-layer PMB. Further, to improve the bearing characteristics, multi-layers are arranged, one adjacent to the other, and provided an air gap between adjacent layers in the axial direction. Providing a copper plate on the surface of the rotor enhances the damping property of PMB and forms an ECD system. This damping system is simple in construction and is designated as a CECDS (Fig. 1b). In this system, interactions between the eddy currents generated in the conductor and the total magnetic field generate damping forces that dampen the axial and lateral movements of the magnet layers provided on the rotor. To avoid the reduced air gap due to the inclusion of copper plate in NECDS, copper rings are inserted in the axial air gap of the rotor to form a NECDS for an optimized MRPMB, as shown in Fig. 1c.

Fig. 1
figure 1

PMB configurations, a mono-layer radial PMB with CECDS b MRPMB configuration with CECDS c MRPMB configuration with NECDS

Full size image

3 Mathematical model and optimization

Two methods can be used to achieve the optimal characteristics associated with MRPMB. First, by reducing the volume of the magnet necessary force and stiffness values can be attained [32] and second, by maximizing properties in a specific magnet volume [18, 19]. The general semi-analytical equations of radial force and stiffness generated in MRPMB are given by Eq. (1) and (2) [27], respectively. Interactions between the stator and rotor rings are shown in Fig. 2, and the Eqs. (1) and (2) are developed by assuming uniform magnetization of the magnet rings in multi-layer PMB. Uneven magnetization of rings causes vibrations and unbalanced forces which can be reduced using damping systems. Comprehensive design procedures to optimize the bearing specifications and maximize the characteristics of multi-layer radial and thrust PMB were presented in our earlier work [27]. In the generalized optimization procedure, the authors tried to express the radial air gap (g) and axial length of the bearing (L) with respect to outer diameter of the bearing. The values of g/D4 is varied from 0.005 to 0.025 and L/D4 from 0.25 to 1.5. The designer can choose the values of these two ratios in the specified range for the optimization process.

Fig. 2
figure 2

Magnetic forces between the faces of rings in MRPMB [16]

Full size image

In this work, radial PMB is optimized based on three general parameters (g, D4, and L) by following the procedure outlined below and actions; the optimized results are shown in Tables 1 and 2.

  1. 1.

    In the proposed work, arbitrary values of g/D4 = 0.02 and L/D4 = 0.66 are chosen for demonstrating the suitability of the generalized optimization method for different applications.

  2. 2.

    In the present work, g = 1.5 mm is taken, and L = 50 mm and D4 = 75 mm is calculated using this value.

  3. 3.

    Using the curve fit equations, optimum bearing parameters (D1, D2, D3, n, and ag) are calculated for maximum radial force and stiffness.

  4. 4.

    The ratios corresponding to maximized radial force (Fr/Frs) and stiffness (Kr/Krs) are calculated by referring to the curve fit equations.

  5. 5.

    The maximized radial force (Frs) and stiffness (Krs) generated by single ring pair bearing are calculated by using Eqs. (1) and (2).

  6. 6.

    Fr and Kr generated in the optimized MRPMB are obtained following step 4.

$${F}_{r}=\frac{{B}_{r}^{2}}{4\pi {\mu }_{0}}{\sum }_{u=1}^{n}{\sum }_{v=1}^{n}{\sum }_{k=1}^{2}{\sum }_{l=3}^{4}{\sum }_{p=1}^{m}{\sum }_{q=1}^{m}\frac{{S}_{pku}{S}_{qlv}}{{R}_{\left(pku\right)\left(qlv\right)}^{3}}{R}_{\left(pku\right)\left(qlv\right)}{\left(-1\right)}^{\left(u+v\right)}{\left(-1\right)}^{\left(k+l\right)}$$
(1)

where \(=\sqrt{{\left({X}_{qlv}- {X}_{pku}\right)}^{2}+{\left({Y}_{qlv}- {Y}_{pku}\right)}^{2}+{\left({Z}_{qlv}- {Z}_{pku}\right)}^{2}}\)

Table 1 Optimized MRPMB dimensions corresponding to maximum radial force
Full size table
Table 2 Optimized MRPMB dimensions for maximum radial stiffness
Full size table
$${R}_{(pku)(qlv)}=\left({X}_{qlv}-{X}_{pku}\right)i+ \left({Y}_{qlv}-{Y}_{pku}\right)j+ \left({Z}_{qlv}-{Z}_{pku}\right)k$$
$${{(X}_{pku})}_{1, 2}=(x+{r}_{mr}\mathrm{cos}\beta ){\varvec{i}}\,\, {{(X}_{qlv})}_{\mathrm{3,4}}=({r}_{ms}\mathrm{cos}\alpha ){\varvec{i}}$$
$${({Y}_{pku})}_{1, 2}=(y+{r}_{mr}\mathrm{sin}\beta ){\varvec{j}}\,\,{{(Y}_{qlv})}_{\mathrm{3,4}}=({r}_{ms}\mathrm{sin}\alpha ){\varvec{j}}$$
$${{(Z}_{pku})}_{1}=\left((u-1\right)l+\left(u-1\right)ag){\varvec{k}}\,\,{{(Z}_{qlv})}_{3}=(\left(v-1)l+\left(v-1\right)ag\right){\varvec{k}}$$
$${({Z}_{pku})}_{2}=\left((u\right)l+\left(u-1\right)ag){\varvec{k}}{({Z}_{qlv})}_{4}=\left(vl+\left(v-1\right)ag\right){\varvec{k}}$$
$${K}_{r}=\frac{\mathrm{d}{F}_{x}}{\mathrm{d}r}$$
(2)

The bearing configuration has been modeled by creating magnetic rotor and stator rings in the cylindrical control volume. The property of air (relative permeability) is assigned to the control volume. SOLID97 elements are used to mesh the rings and control volume in ANSYS. The properties of N48 NdFeB magnets grade (coercive force, Hc = 895 kA/m and relative permeability, μr = 1.24) are used to magnetize the rings in the alternate opposite axial directions (Fig. 3b). The bearing model is meshed with 7, 99,104 elements. The magnetic flux boundary conditions are applied on the surfaces of the control volume. The bearing rotor is displaced in the radial direction (Fig. 3b). The radial force generated on the rotor is calculated by creating the rotor as a component using magnetic virtual displacement method. The mesh convergence test is also conducted by varying the number of elements of the bearing model.

Fig. 3
figure 3

Bearing configuration. a Isometric view of magnetized bearing rings b eccentric rotor

Full size image

4 Analysis of conventional eddy current damping system

Design and optimization of MRPMB based on general three parameters using indigenously developed semi-analytical equations are presented in Sect. 3. Modeling ECD is a challenging task because the damping forces are generated due to dynamic interactions between the eddy currents of the conductor and a moving magnetic field. The difficulty lies with the calculation of the amount of damping generated. Both analytical simulations and FEA have been used by researchers [24,25,26] in the recent past to estimate damping characteristics of ECD. A more significant amount of error (around 40%) was observed between the results of simplified analytical equations and experimentally measured damping coefficients in [24]. Another approach to model ECD is the 3D transient FEA. This method is more accurate but requires high computational time. In addition, authors in [26] used FEA curve fitting findings in conjunction with a proposed analytical model to evaluate the mechanical impedance characteristics. Considering the above aspects and calculating accurate results, for the proposed damping system, 3D electromagnetic transient analysis is performed in ANSYS to evaluate damping characteristics associated with optimized MRPMB for maximum radial force and stiffness. Initially, optimized MRPMB is modeled using the properties of N48 NdFeB permanent magnet rings with SOLID97 elements, and meshed model consists of 7,99,104 elements and a copper plate of thickness 0.4 mm is then created to cover the rotor to form a damping system. The material properties used in this simulation are listed in Table 3. In the analysis, boundary conditions are imposed by defining the degree of freedom constraints on areas. Firstly, the antisymmetric constraint is generated around the circumference of the control volume, and second by applying an electric scalar potential to the moving component of the bearing system.

Table 3 Material properties of MRPMB with ECD
Full size table

As the rotor gets displaced from its initial position, an eddy current is generated in the copper plate, due to which a magnetic field of opposite polarity is induced. Due to the interaction between the induced magnetic field and the stationary magnetic field, a Lorentz force is generated on the copper plate. Two-step loading is used to achieve the stable magnetic flux in the transient analysis. In the first step, loading flux increases with time, and it becomes constant till the end of the second step loading. Figure 4 depicts the relationship between magnetic flux density and time obtained using ANSYS.

Fig. 4
figure 4

Variation of magnetic flux density with time

Full size image

In damping analysis, the rotor is given a linear velocity in the axial and radial directions, ranging from 0 to 100 m/s with a step size of 10 m/s. The components of damping forces (axial and radial) and corresponding coefficients are calculated at different rotor velocities. In addition, the perpendicular and parallel rotational damping forces are computed by assigning rotational velocity to the rotor. The rotational speed of the rotor is varied from 10 to 100 kRPM in steps of 10 kRPM. The copper plate thickness is varied from 0.1 to 0.5 mm at the velocities at which maximum damping force values are obtained. As per the optimization results (Tables 1 and 2) of radial permanent magnet bearing, the optimized parameters are different for maximum radial force and radial stiffness. Two bearing models are created by considering the concerned optimized parameters, and damping analysis is carried out at maximum radial force and maximum radial stiffness of MRPMB.

4.1 Analysis of damper at maximum radial force

In this section, analysis of the ECD system is carried out for MRPMB at maximum radial force. The calculated axial and radial damping force values are plotted as shown in Fig. 5. The value of axial damping force increases with the velocity and remains unchanged at higher velocities (> 70 m/s), whereas the radial damping force value rises continuously with the velocity. The variation of corresponding damping coefficients is also shown in Fig. 6. The axial and radial damping coefficient values range between 7–17 Ns/m and 175–183 Ns/m, respectively. Figure 7 shows the results of the rotational damping force (i.e., perpendicular and parallel components). The axial component is positive and increases with the rotational velocity, whereas the vertical component is negative and decreases with the rotational velocity. The eddy current and Lorentz force distribution in a copper plate at 10 m/s and 10 kRPM are shown in Fig. 8a and b, respectively.

Fig. 5
figure 5

Damping force results for maximum radial force

Full size image
Fig. 6
figure 6

Damping coefficient results for maximum radial force

Full size image
Fig. 7
figure 7

Rotational damping force vs. rotational speed for maximum radial force

Full size image
Fig. 8
figure 8

Distribution of a eddy current in a copper plate at 10 m/s axial velocity b Lorentz force at 10 kRPM rotational speed

Full size image

In the present ECD system, the copper plate thickness is varied at velocity points where the force values are maximum. Thickness is varied from 0.1 to 0.5 mm with a step size of 0.1 mm at 100 m/s, and variations of force values with thickness are plotted in Figs. 9 and 10. Maximum axial damping force is generated at 0.3 mm thickness, and both radial and rotational forces increase as copper plate thickness increases. The Lorentz force generated is proportional to the generated eddy current and when the conductor plate thickness is increased, this effect gets diluted due to the skin effect when the rotor is moved in the axial direction. The optimum value of axial damping force is generated at 0.3 mm thickness of the plate.

Fig. 9
figure 9

Damping force vs. copper plate thickness a axial damping force b radial damping force

Full size image
Fig. 10
figure 10

Rotational damping force vs. copper plate thickness

Full size image

4.2 Analysis of damper at maximum radial stiffness

The analysis of the ECD system for MRPMB is further extended at maximum radial stiffness. The variations of axial, radial, and rotational damping force values are calculated at different axial, radial, and rotational velocities of the rotor are shown in Figs. 11 and 12. The corresponding damping coefficient values are plotted as shown in Fig. 13. Both axial and radial damping force values increase with the velocity, and the axial damping force values are nearly constant at a velocity above 70 m/s due to skin effect when the rotor is moved in the axial direction. The axial damping coefficient value decreases from 18 to 8 Ns/m, and radial damping coefficient values are almost remained unchanged at 175 Ns/m.

Fig. 11
figure 11

Damping force results for maximum radial stiffness a variation of axial damping force b variation of radial damping force

Full size image
Fig. 12
figure 12

Rotational damping force vs. rotational speed for maximum radial stiffness

Full size image
Fig. 13
figure 13

Damping coefficient results for maximum radial stiffness a variation of axial damping coefficient b variation of radial damping coefficient

Full size image

The variation of perpendicular and parallel components associated with rotational damping force for stiffness shows a similar trend as the maximum force. Optimization of copper plate thickness is carried out for maximum radial stiffness at velocity points where the force values are maximum, and results are plotted in Figs. 14 and 15. A similar trend is observed in the results obtained in the analysis at maximum radial force. Maximum axial damping force occurs at 0.3 mm, and the radial damping force is maximum at 0.5 mm thickness

Fig. 14
figure 14

Damping force vs. copper plate thickness a axial b radial

Full size image
Fig. 15
figure 15

Rotational damping force vs. copper plate thickness

Full size image

5 Analysis of novel eddy current damper

In this section, a damping analysis is performed for the proposed NECDS for an optimized MRPMB for maximum radial force and stiffness. The created model consists of 11,43,746 elements. The rotor has given an eccentricity of 0.75 mm in the x-direction, and no axial offset is provided to the rotor. For the proposed model, copper is used as a conductor material, and magnet rings are of N48 grade. The material listed in Table 1 is used in the simulation. The inner and outer diameters of copper rings are the same as those of rotor rings. An eddy current is generated when the rotor rotates in the copper rings. This current generates the magnetic field of opposite polarity of the magnet, and the force generated due to interaction between magnetic fields is called Lorentz force. In transient analysis, the stable magnetic flux density is achieved by two-step loading; in the first step magnetic flux rises uniformly with time and reaches a maximum value, and in the second step, the magnetic flux is invariable with time. The rotor is given translational velocities ranging from 10 to 100 m/s with 10 m/s step size in the axial and radial directions. The corresponding results are obtained. Rotational damping forces (parallel and perpendicular components) are also calculated by varying the rotating speed from 10 to 100 kRPM with 10 kRPM step size.

5.1 Damping analysis at maximum radial force

The variations of damping forces and their equivalent coefficients for different velocities of the rotor are plotted in Fig. 16. Both the damping force values increase with the velocity and reach maximum values at 100 m/s. The axial damping force values are higher than the radial damping force. On the other hand, the axial damping coefficient fluctuates between 30 and 60 Ns/m, while the radial damping coefficient is approximately almost constant at 30 Ns/m. The perpendicular and parallel components associated with rotational damping force are also plotted, as shown in Fig. 17. The values of the parallel component of the damping force are nearly constant concerning the rotational speed, and the perpendicular damping force component rises continuously. The maximum value is obtained at 100 kRPM. The eddy current and Lorentz force distributions in the copper rings of the rotor are shown in Figs. 18 and 19, respectively. The maximum value of eddy current is generated on the surfaces of the copper rings which are exposed to higher magnetic flux density.

Fig. 16
figure 16

Damping results vs. velocity for maximum radial force a damping force b damping coefficient

Full size image
Fig. 17
figure 17

Rotational damping force vs. rotational speed for maximum radial force

Full size image
Fig. 18
figure 18

Eddy current distribution in rotor for maximum radial force at a 10 m/s axial velocity b 10 m/s radial velocity c 10 kRPM rotational speed

Full size image
Fig. 19
figure 19

Lorentz force distribution in rotor for maximum radial force at a 10 m/s axial velocity b 10 m/s radial velocity c 10 kRPM rotational speed

Full size image

5.2 Damping analysis at maximum radial stiffness

The axial, radial and rotational damping results are calculated in an optimized MRPMB with ECD at maximum radial stiffness, and results are plotted in Figs. 20 and 21. The axial and radial damping force values increase with the velocity. The axial damping coefficient varies between the ranges 30–60 Ns/m, and the radial damping coefficient is almost constant at 30 Ns/m. The perpendicular force component is equal to zero at all rotational speeds of the rotor, and parallel force component values increase with the rotational speed of the rotor. The eddy current and Lorentz force distributions in the copper rings of the rotor are shown in Figs. 22 and 23, respectively. The maximum value of eddy current is generated on the surfaces of the copper rings which are exposed to higher magnetic flux density.

Fig. 20
figure 20

Damping results vs. velocity for maximum radial stiffness a damping force b damping coefficient

Full size image
Fig. 21
figure 21

Rotational damping force vs. rotational speed for maximum radial stiffness

Full size image
Fig. 22
figure 22

Eddy current distribution in rotor at maximum radial stiffness at a 10 m/s axial velocity, b 10 m/s radial velocity, c 10 kRPM rotational speed

Full size image
Fig. 23
figure 23

Lorentz force distribution in a rotor at maximum radial stiffness at a 10 m/s axial velocity, b 10 m/s radial velocity, c 10 kRPM rotational speed

Full size image

6 Conclusion

In this work, analysis of CECDS and NECDS is performed for an optimized MRPMB for maximum radial force and stiffness. Based on the analysis results, the conclusions drawn are given below.

  • MRPMB is designed and optimized for maximum radial force and stiffness based on three general parameters (g/D4 = 0.02 and L/D4 = 0.66, \(g\) = 1.5 mm).

  • The maximized force and stiffness values of an optimized MRPMB are 13.2 and 13.75 times the values of a single ring pair radial bearing structure.

  • The proposed damping systems for an optimized MRPMB provide sufficient damping characteristics to reduce the axial and lateral vibrations of the rotor.

  • In the proposed CECDS, an optimum value of the copper plate thickness (0.3 mm) is observed concerning maximum axial damping force, whereas in the case of radial and rotational damping forces, magnitudes increase with an increase in the copper plate thickness.

  • Damping characteristics of both conventional and novel structures are almost the same at maximum radial force and stiffness.

  • In the novel structure, the axial damping force (3410.15 N at 100 m/s) generated is higher than the conventional one (852.74 N at 100 m/s).

  • Radial damping force generated in the conventional structure (17,689.1 N at 100 m/s) is much higher than the novel one (2701.7 N at 100 m/s).

  • The axial damping coefficient of the novel structure (57.53 Ns/m at 10 m/s) is higher as compared to the conventional one (17.85 Ns/m at 10 m/s).

  • The radial damping coefficient of conventional structure (182.46 Ns/m at 10 m/s) is much higher as compared to the novel one (31.77 Ns/m at 10 m/s).

  • The parallel component of a rotational damping force is almost equal to zero in the novel structure whereas, in a conventional system, its maximum value is 1541.12 N at 100 kRPM.

  • The perpendicular component of a rotational damping force is much higher in the case of conventional structure (5179.52 N at 100 kRPM) as compared to novel one (571.73 N at 100 kRPM).

Based on the analysis results, NECDS can replace CECDS for an optimized MRPMB without reducing the radial air gap for better performance features.