Skip to main content
SpringerLink
Log in

Influence of initial stress and gravity on refraction and reflection of SV wave at interface between two viscoelastic liquid under three thermoelastic theories

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

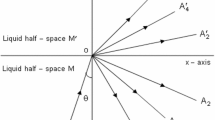
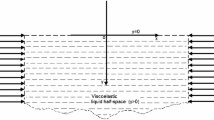
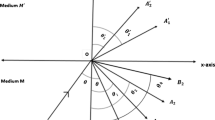
This approach is to examine the impact of magnetic field, viscosity, gravity and initial stress on SV wave while traveling through the interface of two visco-thermoelastic liquid layers. The basic equations in context of three theories have been discussed to drive results for refracted thermal and P waves and reflected thermal, SV and P waves. After using the boundary conditions the amplitude ratios have been computed in matrix form.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Abbreviations

P :

Initial stress

\(\overrightarrow {\acute\omega }\) :

Local rotation

\({\acute{s}}_{11}\) :

Principal or incremental stress component along x axis

\({\acute{s}}_{22}\) :

Principal or incremental stress components along y axis

\({\acute{s}}_{21}\) :

Shear stress component

S 11 :

Normal initial stress component along x axis

S 22 :

Normal initial stress component along y axis

ρ :

Density of medium

u :

Component of displacement along x axis

v :

Component of displacement along y axis

F 1 :

Lorent’z force along x axis

F 2 :

Lorent’z force along y axis

 \(\gimel\), μ :

Lame’s constant

d xy :

Shear strain component

d xx :

Principal strain component

α t :

Coefficient of linear thermal expansion

K :

Bulk modulus

T :

Absolute temperature

τ 1 :

Relaxation time

c e :

Specific heat per unit mass

ϑ :

Thermal conductivity

\({\mathbf{\mathcal{B}}}\) :

Electric intensity vector

°:

Perturbed magnetic field vector

\(\varvec{H}\) :

Magnetic field vector

\(\varvec{J}\) :

Electric current density vector

\(\in_{0}\) :

Electric permeability

μe :

Magnetic permeability

R H :

Magnetic pressure number

c 1 :

Elastic wave velocity

c 2 :

Rotational wave velocity

ζ :

Initial stress parameter

ω :

Circular frequency

k :

Wave number

ɛ T :

Thermoelastic coupling constant

τ θ :

Phase lag of gradient of temperature

d :

Strain component

References

  1. Dhaliwal RS, Singh A (1980) Dynamic coupled thermoelasticity Hindustan Publ. Corp, New Delhi

    Google Scholar 

  2. Lord HW, Shulman Y (1967) A generalized dynamical theory of thermoelasticity. J Mech Phys Solids 15(5):299–309

    Article  MATH  Google Scholar 

  3. Green AE, Lindsay KA (1972) Thermoelasticity. J Elast 2(1):1–7

    Article  MATH  Google Scholar 

  4. RoyChoudhuri SK (2007) One-dimensional thermoelastic waves in elastic half-space with dual phase-lag effects. J Mech Mater Struct 2(3):489–503

    Article  Google Scholar 

  5. Abouelregal Ahmed E, Abo-Dahab SM (2012) Dual phase lag model on magneto-thermoelasticity infinite non-homogeneous solid having a spherical cavity. J Therm Stresses 35(9):820–841

    Article  Google Scholar 

  6. Sheikholeslami Mohsen (2017) Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J Mol Liq 229:137–147

    Article  Google Scholar 

  7. Sheikholeslami Mohsen (2017) Numerical simulation of magnetic nanofluid natural convection in porous media. Phys Lett A 381(5):494–503

    Article  Google Scholar 

  8. Sheikholeslami M, Rokni HB (2017) Nanofluid two phase model analysis in existence of induced magnetic field. Int J Heat Mass Transf 107:288–299

    Article  Google Scholar 

  9. Sheikholeslami M (2017) Influence of Coulomb forces on Fe 3 O 4–H 2 O nanofluid thermal improvement. Int J Hydrogen Energy 42(2):821–829

    Article  Google Scholar 

  10. Kandelousi Mohsen Sheikholeslami (2014) Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition. Eur Phys J Plus 11(129):1–12

    Google Scholar 

  11. Sheikholeslami M, Hayat T, Alsaedi A (2017) Numerical simulation of nanofluid forced convection heat transfer improvement in existence of magnetic field using lattice Boltzmann method. Int J Heat Mass Transf 108:1870–1883

    Article  Google Scholar 

  12. Sheikholeslami M, Bhatti MM (2017) Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. Int J Heat Mass Transf 111:1039–1049

    Article  Google Scholar 

  13. Sheikholeslami M, Hayat T, Alsaedi A (2017) Numerical study for external magnetic source influence on water based nanofluid convective heat transfer. Int J Heat Mass Transf 106:745–755

    Article  Google Scholar 

  14. Sheikholeslami M, Houman B (2017) Rokni. “Numerical modeling of nanofluid natural convection in a semi annulus in existence of Lorentz force.”. Comput Methods Appl Mech Eng 317:419–430

    Article  Google Scholar 

  15. Abd-Alla AM, Abo-Dahab SM, Kilany AA (2016) SV-waves incidence at interface between solid-liquid media under electromagnetic field and initial stress in the context of three thermoelastic theories. J Therm Stresses 39(8):960–976

    Article  Google Scholar 

  16. Sharma JN, Chauhan RS (1999) On the problems of body forces and heat sources in thermoelasticity without energy dissipation. Indian J Pure Appl Math 30:595–610

    MATH  Google Scholar 

  17. Chakraborty N, Singh MC (2011) Reflection and refraction of a plane thermoelastic wave at a solid–solid interface under perfect boundary condition, in presence of normal initial stress. Appl Math Model 35(11):5286–5301

    Article  MathSciNet  MATH  Google Scholar 

  18. Deswal S, Tomar SK, Kumar R (2000) Effect of fluid viscosity on wave propagation in a cylindrical bore in micropolar elastic medium. Sadhana 25(5):439–452

    Article  Google Scholar 

  19. Singh MC, Chakraborty N (2016) Reflection and refraction of plane waves at the interface of two visco-thermoelastic liquid layers in presence of magnetic field and compressional stress, with the outer core inside the earth as a model. Int J Appl Comput Math 3(3):2107–2124

    Article  MathSciNet  Google Scholar 

  20. De SN, Sen-Gupta PR (1974) Influence of gravity on wave propagation in an elastic layer. J Acoust Soc Am 55(5):919–921

    Article  Google Scholar 

  21. Acharya DP, Roy I, Sengupta S (2009) Effect of magnetic field and initial stress on the propagation of interface waves in transversely isotropic perfectly conducting media. Acta Mech 202(1):35–45

    Article  MATH  Google Scholar 

  22. Biot MA, Drucker DC (1965) Mechanics of incremental deformation. J Appl Mech 32:957

    Article  Google Scholar 

  23. Ewing WM, Jardetzky WS, Press F, Beiser A (1957) Elastic waves in layered media. Phys Today 10:27

    Article  MATH  Google Scholar 

  24. Dziewonski AM, Anderson DL (1981) Preliminary reference Earth model. Phys Earth Planet Inter 25(4):297–356

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, International Islamic University, Islamabad, 44000, Pakistan

    A. A. Khan & A. Afzal

Authors
  1. A. A. Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Afzal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. A. Khan.

Additional information

Technical Editor: Cezar Negrao.

Appendix

Appendix

$$m_{1} = - \frac{A}{4} - \frac{1}{2}\sqrt p - \frac{1}{2}\sqrt {\left( {q - z} \right)}$$
$$m_{2} = - \frac{A}{4} - \frac{1}{2}\sqrt p + \frac{1}{2}\sqrt {\left( {q - z} \right)}$$
$$m_{3} = - \frac{A}{4} + \frac{1}{2}\sqrt p - \frac{1}{2}\sqrt {\left( {q - z} \right)}$$
$$m_{4} = - \frac{A}{4} + \frac{1}{2}\sqrt p + \frac{1}{2}\sqrt {\left( {q - z} \right)}$$
$$m_{5} = \frac{1}{{2c_{2}^{2} }}\left( {g - \sqrt {\left( g \right)^{2} - 4k^{2} c^{2} \alpha c_{2}^{2} + 4k^{2} c_{2}^{4} } } \right)$$
$$m_{6} = \frac{1}{{2c_{2}^{2} }}\left( {g + \sqrt {\left( g \right)^{2} - 4k^{2} c^{2} \alpha c_{2}^{2} + 4k^{2} c_{2}^{4} } } \right)$$
$$m_{7} = \frac{2}{3}k \eta \omega$$
$$p = \frac{{A^{2} }}{4} - \frac{2B}{3} + \frac{{2^{{\frac{1}{3}}} \left( {B^{2} + 12D - 3AC} \right)}}{3h} + \frac{1}{{3*2^{{\frac{1}{3}}} }}h$$
$$q = \frac{{A^{2} }}{2} - \frac{4B}{3} - \frac{{2^{{\frac{1}{3}}} \left( {B^{2} + 12D - 3AC} \right)}}{3h} - \frac{1}{{3*2^{{\frac{1}{3}}} }}h$$
$$h = \left( {O + \sqrt {\left( { - 4\left( {B^{2} + 12D - 3AC} \right)^{3} + \left( O \right)^{2} } \right)} } \right)^{{\frac{1}{3}}}$$
$$O = 2B^{3} + 27A^{2} D - 72BD - 9ABC + 27C^{2}$$
$$l_{1} = K\left( { - k^{2} + m_{2}^{2} } \right) - \frac{2}{3}\eta k^{2} \omega - \frac{4}{3}\eta m_{2}^{2} i\omega - \gamma b_{2} - \tau_{1} i\omega b_{2}$$
$$l_{2} = K\left( { - k^{2} + m_{4}^{2} } \right) - \frac{2}{3}\eta k^{2} \omega - \frac{4}{3}\eta m_{4}^{2} i\omega - \gamma b_{4} - \tau_{1} i\omega b_{4}$$
$$l_{3} = - \frac{2}{3}k \eta \omega$$
$$b_{1} = \frac{\rho }{\gamma \tau }\left( { - c_{1}^{2} k^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3}} \right) + m_{1}^{2} c_{1}^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3} - gm_{1} } \right)} \right)$$
$$b_{2} = \frac{\rho }{\gamma \tau }\left( { - c_{1}^{2} k^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3}} \right) + m_{2}^{2} c_{1}^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3} - gm_{2} } \right)} \right)$$
$$b_{3} = \frac{\rho }{\gamma \tau }\left( { - c_{1}^{2} k^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3}} \right) + m_{3}^{2} c_{1}^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3} - gm_{3} } \right)} \right)$$
$$b_{4} = \frac{\rho }{\gamma \tau }\left( { - c_{1}^{2} k^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3}} \right) + m_{4}^{2} c_{1}^{2} \left( {1 + R_{H} + \zeta - \frac{i4\eta \omega }{3} - gm_{4} } \right)} \right)$$

All variables for second medium are same with dashes.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, A.A., Afzal, A. Influence of initial stress and gravity on refraction and reflection of SV wave at interface between two viscoelastic liquid under three thermoelastic theories. J Braz. Soc. Mech. Sci. Eng. 40, 208 (2018). https://doi.org/10.1007/s40430-018-1103-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1103-y

Keywords

Search

Navigation