Skip to main content
SpringerLink
Log in

Interlayer effects of Van der Waals interactions on transverse vibrational behavior of bilayer graphene sheets

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

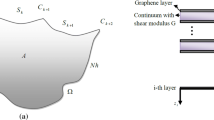
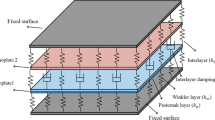
This study focuses only on the interlayer effects of van der Waals (VdWs) interactions (including simultaneous effects of shear and tensile-compressive effects) on the free transverse vibrational behavior of bilayer graphene sheets by implementing the classical continuum mechanics theory. To this end, the classical sandwich plate theory and the Hamilton’s principle are involved to obtain the governing equations and the harmonic differential quadrature method is employed to calculate the natural frequencies and related mode shapes. The results show the shear effect of VdWs interactions has significant influences on primary natural frequencies and mode shapes. Therefore it is a main determinant and can safely assume the pure shear effect while designing sensors, actuators, accelerometers and resonators. Finally, the potential depth parameter is introduced to consider the simultaneous effects of shear and tensile-compressive forces.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Allen MJ, Tung VC, Kaner RB (2009) Honeycomb carbon: a review of graphene. Chem Rev 110:132–145. https://doi.org/10.1021/cr900070d

    Article  Google Scholar 

  2. Siochi EJ (2014) Graphene in the sky and beyond. Nat Nanotechnol 9:745–747. https://doi.org/10.1038/nnano.2014.231

    Article  Google Scholar 

  3. Avouris P (2010) Graphene: electronic and photonic properties and devices. Nano Lett 10:4285–4294

    Article  Google Scholar 

  4. Balandin AA (2011) Thermal properties of graphene and nanostructured carbon materials. Nat Mater 10:569–581

    Article  Google Scholar 

  5. Bunch JS, van der Zande AM, Verbridge SS, Frank IW, Tanenbaum DM, Parpia JM et al (2007) Electromechanical resonators from graphene sheets. Science 315:490–493. https://doi.org/10.1126/science.1136836

    Article  Google Scholar 

  6. Aksencer T, Aydogdu M (2011) Levy type solution method for vibration and buckling of nanoplates using nonlocal elasticity theory. Physica E 43:954–959

    Article  Google Scholar 

  7. Ansari R, Arash B, Rouhi H (2011) Vibration characteristics of embedded multi-layered graphene sheets with different boundary conditions via nonlocal elasticity. Compos Struct 93:2419–2429

    Article  Google Scholar 

  8. Ansari R, Sahmani S (2013) Prediction of biaxial buckling behavior of single-layered graphene sheets based on nonlocal plate models and molecular dynamics simulations. Appl Math Model 37:7338–7351

    Article  MathSciNet  Google Scholar 

  9. Arani AG, Haghparast E, Zarei HB (2016) Nonlocal vibration of axially moving graphene sheet resting on orthotropic visco-Pasternak foundation under longitudinal magnetic field. Physica B 495:35–49

    Article  Google Scholar 

  10. Farajpour A, Shahidi AR, Mohammadi M, Mahzoon M (2012) Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Compos Struct 94:1605–1615

    Article  Google Scholar 

  11. He XQ, Kitipornchai S, Liew KM (2005) Resonance analysis of multi-layered graphene sheets used as nanoscale resonators. Nanotechnology 16:2086

    Article  Google Scholar 

  12. He XQQ, Wang JBB, Liu B, Liew KMKM (2012) Analysis of nonlinear forced vibration of multi-layered graphene sheets. Comput Mater Sci 61:194–199. https://doi.org/10.1016/j.commatsci.2012.03.043

    Article  Google Scholar 

  13. Jomehzadeh E, Saidi AR (2011) A study on large amplitude vibration of multilayered graphene sheets. Comput Mater Sci 50:1043–1051. https://doi.org/10.1016/j.commatsci.2010.10.045

    Article  Google Scholar 

  14. Lin RM (2012) Nanoscale vibration characteristics of multi-layered graphene sheets. Mech Syst Sign Process 29:251–261. https://doi.org/10.1016/j.ymssp.2011.11.005

    Article  Google Scholar 

  15. Lin RM (2012) Nanoscale vibration characterization of multi-layered graphene sheets embedded in an elastic medium. Comput Mater Sci 53:44–52. https://doi.org/10.1016/j.commatsci.2011.08.012

    Article  Google Scholar 

  16. Mohammadi M, Farajpour A, Moradi A, Ghayour M (2014) Shear buckling of orthotropic rectangular graphene sheet embedded in an elastic medium in thermal environment. Compos B Eng 56:629–637

    Article  Google Scholar 

  17. Mohammadi M, Goodarzi M, Ghayour M, Farajpour A (2013) Influence of in-plane pre-load on the vibration frequency of circular graphene sheet via nonlocal continuum theory. Compos B Eng 51:121–129

    Article  Google Scholar 

  18. Murmu T, Adhikari S (2011) Nonlocal vibration of bonded double-nanoplate-systems. Compos B Eng 42:1901–1911. https://doi.org/10.1016/j.compositesb.2011.06.009

    Article  Google Scholar 

  19. Murmu T, Pradhan SC (2009) Small-scale effect on the free in-plane vibration of nanoplates by nonlocal continuum model. Physica E 41:1628–1633. https://doi.org/10.1016/j.physe.2009.05.013

    Article  Google Scholar 

  20. Narendar S, Gopalakrishnan S (2012) Scale effects on buckling analysis of orthotropic nanoplates based on nonlocal two-variable refined plate theory. Acta Mech 223:395–413

    Article  MathSciNet  MATH  Google Scholar 

  21. Nazemnezhad R (2015) Nonlocal Timoshenko beam model for considering shear effect of van der Waals interactions on free vibration of multilayer graphene nanoribbons. Compos Struct 133:522–528

    Article  Google Scholar 

  22. Nazemnezhad R, Hosseini-Hashemi S (2014) Free vibration analysis of multi-layer graphene nanoribbons incorporating interlayer shear effect via molecular dynamics simulations and nonlocal elasticity. Phys Lett A 378:3225–3232. https://doi.org/10.1016/j.physleta.2014.09.037

    Article  MathSciNet  Google Scholar 

  23. Nazemnezhad R, Shokrollahi H, Hosseini-Hashemi S (2014) Sandwich beam model for free vibration analysis of bilayer graphene nanoribbons with interlayer shear effect. J Appl Phys 115:174303. https://doi.org/10.1063/1.4874221

    Article  Google Scholar 

  24. Nazemnezhad R, Zare M (2016) Nonlocal Reddy beam model for free vibration analysis of multilayer nanoribbons incorporating interlayer shear effect. Eur J Mech A Solids 55:234–242. https://doi.org/10.1016/j.euromechsol.2015.09.006

    Article  MathSciNet  Google Scholar 

  25. Pouresmaeeli S, Fazelzadeh SA, Ghavanloo E (2012) Exact solution for nonlocal vibration of double-orthotropic nanoplates embedded in elastic medium. Compos Part B Eng 43:3384–3390. https://doi.org/10.1016/j.compositesb.2012.01.046

    Article  Google Scholar 

  26. Shen Z-B, Tang H-L, Li D-K, Tang G-J (2012) Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput Mater Sci 61:200–205

    Article  Google Scholar 

  27. Ansari R, Arash B, Rouhi H (2011) Nanoscale vibration analysis of embedded multi-layered graphene sheets under various boundary conditions. Comput Mater Sci 50:3091–3100

    Article  Google Scholar 

  28. Robertson DH, Brenner DW, Mintmire JW (1992) Energetics of nanoscale graphitic tubules. Phys Rev B 45:12592

    Article  Google Scholar 

  29. Lu JP (1997) Elastic properties of carbon nanotubes and nanoropes. Phys Rev Lett 79:10

    Article  MathSciNet  Google Scholar 

  30. Jin Y, Yuan FG (2003) Simulation of elastic properties of single-walled carbon nanotubes. Compos Sci Technol 63:1507–1515

    Article  Google Scholar 

  31. Striz AG, Wang X, Bert CW (1995) Harmonic differential quadrature method and applications to analysis of structural components. Acta Mech 111:85–94. https://doi.org/10.1007/BF01187729

    Article  MATH  Google Scholar 

  32. Shu C (2000) Differential quadrature and its application in engineering. Springer, London

    Book  MATH  Google Scholar 

  33. Kordkheili SAH, Moshrefzadeh-Sani H (2013) Mechanical properties of double-layered graphene sheets. Comput Mater Sci 69:335–343. https://doi.org/10.1016/j.commatsci.2012.11.027

    Article  Google Scholar 

  34. Nazemnezhad R, Zare M, Hosseini-Hashemi S, Shokrollahi H (2016) Molecular dynamics simulation for interlayer interactions of graphene nanoribbons with multiple layers. Superlattices Microstruct 98:228–234

    Article  Google Scholar 

  35. Van Lier G, Van Alsenoy C, Van Doren V, Geerlings P (2000) Ab initio study of the elastic properties of single-walled carbon nanotubes and graphene. Chem Phys Lett 326:181–185. https://doi.org/10.1016/S0009-2614(00)00764-8

    Article  Google Scholar 

  36. Politano A, Chiarello G (2015) Probing the Young’s modulus and Poisson’s ratio in graphene/metal interfaces and graphite: a comparative study. Nano Res 8:1847–1856

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Iran University of Science and Technology, Narmak, Tehran, Iran

    Kamran Kamali

  2. Department of Design, Fateh Sanat Kimia Company, Great Industrial Zone, Shiraz, Iran

    Kamran Kamali

  3. School of Engineering, Damghan University, Damghan, 36716-41167, Iran

    Reza Nazemnezhad

  4. Department of Mechanical and Manufacturing Engineering, Schulich School of Engineering, University of Calgary, 40 Research Place NW, Calgary, Alberta, T2L 1Y6, Canada

    Mojtaba Zare

Authors
  1. Kamran Kamali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Reza Nazemnezhad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mojtaba Zare
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reza Nazemnezhad.

Appendix

Appendix

$$ - \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} u_{1} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} v_{1} }}{\partial x\partial y}} \right) - \frac{{E_{f} h_{f} }}{2(1 + \nu )}\left( {\frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{1} }}{\partial x\partial y}} \right) + \frac{{G_{xz}^{c} }}{{h_{c} }}\left[ {u_{1} - u_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial x} + \frac{{\partial w_{2} }}{\partial x}} \right)} \right] + I_{0} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} = 0 $$
(63)
$$ - \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} u_{2} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} v_{2} }}{\partial x\partial y}} \right) - \frac{{E_{f} h_{f} }}{2(1 + \nu )}\left( {\frac{{\partial^{2} u_{2} }}{{\partial y^{2} }} + \frac{{\partial^{2} v_{2} }}{\partial x\partial y}} \right) - \frac{{G_{xz}^{c} }}{{h_{c} }}\left[ {u_{1} - u_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial x} + \frac{{\partial w_{2} }}{\partial x}} \right)} \right] + I_{0} \frac{{\partial^{2} u_{2} }}{{\partial t^{2} }} = 0 $$
(64)
$$ - \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} v_{1} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} u_{1} }}{\partial x\partial y}} \right) - \frac{{E_{f} h_{f} }}{2(1 + \nu )}\left( {\frac{{\partial^{2} v_{1} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{1} }}{\partial x\partial y}} \right) + \frac{{G_{yz}^{c} }}{{h_{c} }}\left[ {v_{1} - v_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial y} + \frac{{\partial w_{2} }}{\partial y}} \right)} \right] + I_{0} \frac{{\partial^{2} v_{1} }}{{\partial t^{2} }} = 0 $$
(65)
$$ - \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial^{2} v_{2} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} u_{2} }}{\partial x\partial y}} \right) - \frac{{E_{f} h_{f} }}{2(1 + \nu )}\left( {\frac{{\partial^{2} v_{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{2} }}{\partial x\partial y}} \right) - \frac{{G_{yz}^{c} }}{{h_{c} }}\left[ {v_{1} - v_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial y} + \frac{{\partial w_{2} }}{\partial y}} \right)} \right] + I_{0} \frac{{\partial^{2} v_{2} }}{{\partial t^{2} }} = 0 $$
(66)
$$ \begin{aligned} D\left( {\frac{{\partial^{4} w_{1} }}{{\partial x^{4} }} + \frac{{\partial^{4} w_{1} }}{{\partial y^{4} }} + 2\nu \frac{{\partial^{4} w_{1} }}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{E_{f} h_{f}^{3} }}{6(1 + \nu )}\frac{{\partial^{4} w_{1} }}{{\partial x^{2} \partial y^{2} }} + \frac{{E_{c} }}{{h_{c} }}(w_{1} - w_{2} ) \\ & \quad - \frac{{h_{c} }}{12}\left( {G_{xz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} - G_{xz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} - G_{yz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right) \\ & \quad - \frac{1}{2}\left( {1 + \frac{{h_{f} }}{{h_{c} }}} \right)\left( \begin{aligned} G_{xz}^{c} \frac{{\partial u_{1} }}{\partial x} - G_{xz}^{c} \frac{{\partial u_{2} }}{\partial x} + G_{yz}^{c} \frac{{\partial v_{1} }}{\partial y} - G_{yz}^{c} \frac{{\partial v_{2} }}{\partial y} \hfill \\ + \frac{{h_{f} + h_{c} }}{2}\left( {G_{xz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + G_{xz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right) \hfill \\ \end{aligned} \right) + I_{0} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }} = 0 \\ \end{aligned} $$
(67)
$$ \begin{aligned} & D\left( {\frac{{\partial^{4} w_{2} }}{{\partial x^{4} }} + \frac{{\partial^{4} w_{2} }}{{\partial y^{4} }} + 2\nu \frac{{\partial^{4} w_{2} }}{{\partial x^{2} \partial y^{2} }}} \right) + \frac{{E_{f} h_{f}^{3} }}{6(1 + \nu )}\frac{{\partial^{4} w_{2} }}{{\partial x^{2} \partial y^{2} }} - \frac{{E_{c} }}{{h_{c} }}(w_{1} - w_{2} ) \\ & \quad + \frac{{h_{c} }}{12}\left( {G_{xz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} - G_{xz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} - G_{yz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right) \\ & \quad - \frac{1}{2}\left( {1 + \frac{{h_{f} }}{{h_{c} }}} \right)\left( {G_{xz}^{c} \frac{{\partial u_{1} }}{\partial x} - G_{xz}^{c} \frac{{\partial u_{2} }}{\partial x} + G_{yz}^{c} \frac{{\partial v_{1} }}{\partial y} - G_{yz}^{c} \frac{{\partial v_{2} }}{\partial y}} \right. \\ & \quad \left. { + \frac{{h_{f} + h_{c} }}{2}\left( {G_{xz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + G_{xz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} + G_{yz}^{c} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right)} \right) + I_{0} \frac{{\partial^{2} w_{2} }}{{\partial t^{2} }} = 0 \\ \end{aligned} $$
(68)
$$ \begin{aligned} y = 0(n = y,\,s = x); \\ \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial v_{1} }}{\partial y} + \nu \frac{{\partial u_{1} }}{\partial x}} \right) = \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial v_{2} }}{\partial y} + \nu \frac{{\partial u_{2} }}{\partial x}} \right) = G_{f} h_{f} \left( {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial v_{1} }}{\partial x}} \right) = G_{f} h_{f} \left( {\frac{{\partial u_{2} }}{\partial y} + \frac{{\partial v_{2} }}{\partial x}} \right) \\ & = - D\left( {\frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }}} \right) = - D\left( {\frac{{\partial^{2} w_{2} }}{{\partial y^{2} }} + \nu \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }}} \right) = \\ & \quad - D\left( {\frac{{\partial^{3} w_{1} }}{{\partial y^{3} }} + \nu \frac{{\partial^{3} w_{1} }}{{\partial y\partial x^{2} }}} \right) - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{1} }}{{\partial x^{2} \partial y}} \\ & \quad + \frac{{h_{f} + h_{c} }}{{2h_{c} }}G_{yz}^{c} \left[ {v_{1} - v_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial y} + \frac{{\partial w_{2} }}{\partial y}} \right)} \right] + \frac{1}{{h_{c} }}\frac{{G_{yz}^{c} h_{c}^{2} }}{12}\left( {\frac{{\partial w_{1} }}{\partial y} - \frac{{\partial w_{2} }}{\partial y}} \right) \\ & \quad - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{1} }}{{\partial x^{2} \partial y}} \\ & = - D\left( {\frac{{\partial^{3} w_{2} }}{{\partial y^{3} }} + \nu \frac{{\partial^{3} w_{2} }}{{\partial y\partial x^{2} }}} \right) - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{2} }}{{\partial x^{2} \partial y}} \\ & \quad + \frac{{h_{f} + h_{c} }}{{2h_{c} }}G_{yz}^{c} \left[ {v_{1} - v_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial y} + \frac{{\partial w_{2} }}{\partial y}} \right)} \right] - \frac{1}{{h_{c} }}\frac{{G_{yz}^{c} h_{c}^{2} }}{12}\left( {\frac{{\partial w_{1} }}{\partial y} - \frac{{\partial w_{2} }}{\partial y}} \right) \\ & \quad - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{2} }}{{\partial x^{2} \partial y}} = 0 \\ \end{aligned} $$
(69)
$$ \begin{aligned} x = 0(n = x,\,s = y); \\ \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial u_{1} }}{\partial x} + \nu \frac{{\partial v_{1} }}{\partial y}} \right) = \frac{{E_{f} h_{f} }}{{1 - \nu^{2} }}\left( {\frac{{\partial u_{2} }}{\partial x} + \nu \frac{{\partial v_{2} }}{\partial y}} \right) = G_{f} h_{f} \left( {\frac{{\partial u_{1} }}{\partial y} + \frac{{\partial v_{1} }}{\partial x}} \right) = G_{f} h_{f} \left( {\frac{{\partial u_{2} }}{\partial y} + \frac{{\partial v_{2} }}{\partial x}} \right) \\ & = - D\left( {\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }}} \right) = - D\left( {\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + \nu \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right) = \\ & \quad - D\left( {\frac{{\partial^{3} w_{1} }}{{\partial x^{3} }} + \nu \frac{{\partial^{3} w_{1} }}{{\partial x\partial y^{2} }}} \right) - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{1} }}{{\partial x\partial y^{2} }} \\ & \quad + \frac{{h_{f} + h_{c} }}{{2h_{c} }}G_{xz}^{c} \left[ {u_{1} - u_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial x} + \frac{{\partial w_{2} }}{\partial x}} \right)} \right] + \frac{1}{{h_{c} }}\frac{{G_{xz}^{c} h_{c}^{2} }}{12}\left( {\frac{{\partial w_{1} }}{\partial x} - \frac{{\partial w_{2} }}{\partial x}} \right) \\ & \quad - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{1} }}{{\partial x\partial y^{2} }} = \\ & \quad - D\left( {\frac{{\partial^{3} w_{2} }}{{\partial x^{3} }} + \nu \frac{{\partial^{3} w_{2} }}{{\partial x\partial y^{2} }}} \right) - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{2} }}{{\partial x\partial y^{2} }} \\ & \quad + \frac{{h_{f} + h_{c} }}{{2h_{c} }}G_{xz}^{c} \left[ {u_{1} - u_{2} + \frac{{h_{f} + h_{c} }}{2}\left( {\frac{{\partial w_{1} }}{\partial x} + \frac{{\partial w_{2} }}{\partial x}} \right)} \right] - \frac{1}{{h_{c} }}\frac{{G_{xz}^{c} h_{c}^{2} }}{12}\left( {\frac{{\partial w_{1} }}{\partial x} - \frac{{\partial w_{2} }}{\partial x}} \right) \\ & \quad - \frac{{E_{f} h_{f}^{3} }}{12(1 + \nu )}\frac{{\partial^{3} w_{2} }}{{\partial x\partial y^{2} }} = 0 \\ \end{aligned} $$
(70)
$$ \begin{aligned} y = b(n = y,\,s = x); \hfill \\ u_{1} = u_{2} = v_{1} = v_{2} = w_{1} = w_{2} = \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} = \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }} = 0 \hfill \\ \end{aligned} $$
(71)
$$ \begin{aligned} x = a(n = x,\,s = y); \hfill \\ u_{1} = u_{2} = v_{1} = v_{2} = w_{1} = w_{2} = \frac{{\partial w_{1} }}{\partial x} = \frac{{\partial w_{2} }}{\partial x} = 0 \hfill \\ \end{aligned} $$
(72)
$$ \begin{aligned} x = y = 0; \hfill \\ \frac{{\partial^{2} w_{1} }}{\partial x\partial y} = \frac{{\partial^{2} w_{2} }}{\partial x\partial y} = 0 \hfill \\ \end{aligned} $$
(73)
$$ \begin{aligned} \left( {\frac{{h_{f}^{3} h}}{{12(1 - \nu^{2} )a^{4} }}} \right)\mathop \sum \limits_{n = 1}^{N} D_{in} \bar{W}_{1} (X_{n} ,Y_{j} ) + \left( {\frac{{h_{f}^{3} h}}{{12(1 - \nu^{2} )b^{4} }}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{D}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) \\ & \quad + \left( {\frac{{h_{f}^{3} h}}{{6(1 - \nu^{2} )a^{2} b^{2} }}} \right)\mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{m = 1}^{M} B_{in} \bar{B}_{jm} \bar{W}_{1} (X_{n} ,Y_{m} ) + \left( {\frac{{E_{c} h}}{{E_{f} h_{c} }}} \right)\left( {\bar{W}_{1} (X_{i} ,Y_{j} ) - \bar{W}_{2} (X_{i} ,Y_{j} )} \right) \\ & \quad - \left( {\frac{{G_{xz}^{c} h_{c} h}}{{12E_{f} a^{2} }}} \right)\left( {\mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{1} (X_{n} ,Y_{j} ) - \mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{2} (X_{n} ,Y_{j} )} \right) \\ & \quad - \left( {\frac{{G_{yz}^{c} h_{c} h}}{{12E_{f} b^{2} }}} \right)\left( {\mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) - \mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{2} (X_{i} ,Y_{m} )} \right) \\ & \quad - \left( {\frac{{G_{xz}^{c} h(h_{f} + h_{c} )}}{{2E_{f} h_{c} a}}} \right)\left( {\mathop \sum \limits_{n = 1}^{N} A_{in} \bar{U}_{1} (X_{n} ,Y_{j} ) - \mathop \sum \limits_{n = 1}^{N} A_{in} \bar{U}_{2} (X_{n} ,Y_{j} )} \right) \\ & \quad - \left( {\frac{{G_{yz}^{c} h(h_{f} + h_{c} )}}{{2E_{f} h_{c} b}}} \right)\left( {\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{V}_{1} (X_{i} ,Y_{m} ) - \mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{V}_{2} (X_{i} ,Y_{m} )} \right) \\ & \quad - \left( {\frac{{G_{xz}^{c} h(h_{f} + h_{c} )^{2} }}{{4E_{f} h_{c} a^{2} }}} \right)\left( {\mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{1} (X_{n} ,Y_{j} ) + \mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{2} (X_{n} ,Y_{j} )} \right) \\ & \quad - \left( {\frac{{G_{yz}^{c} h(h_{f} + h_{c} )^{2} }}{{4E_{f} h_{c} b^{2} }}} \right)\left( {\mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) + \mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{2} (X_{i} ,Y_{m} )} \right) = \left( {\frac{{I_{0} \omega^{2} h}}{{E_{f} }}} \right)\bar{W}_{1} (X_{i} ,Y_{j} ) \\ \end{aligned} $$
(74)
$$ \begin{aligned} \left( {\frac{h}{b}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{V}_{1} (X_{i} ,Y_{m} ) + \left( {\frac{\nu h}{a}} \right)\mathop \sum \limits_{n = 1}^{N} A_{in} \bar{U}_{1} (X_{n} ,Y_{j} ) \\ & = \left( {\frac{h}{b}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{V}_{2} (X_{i} ,Y_{m} ) + \left( {\frac{\nu h}{a}} \right)\mathop \sum \limits_{n = 1}^{N} A_{in} \bar{U}_{2} (X_{n} ,Y_{j} ) \\ & = \left( {\frac{h}{b}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{U}_{1} (X_{i} ,Y_{m} ) + \left( {\frac{h}{a}} \right)\mathop \sum \limits_{n = 1}^{N} A_{in} \bar{V}_{1} (X_{n} ,Y_{j} ) \\ & = \left( {\frac{h}{b}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{U}_{2} (X_{i} ,Y_{m} ) + \left( {\frac{h}{a}} \right)\mathop \sum \limits_{n = 1}^{N} A_{in} \bar{V}_{2} (X_{n} ,Y_{j} ) \\ & = \left( {\frac{{h^{2} }}{{b^{2} }}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) + \left( {\frac{{\nu h^{2} }}{{a^{2} }}} \right)\mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{1} (X_{n} ,Y_{j} ) \\ & = \left( {\frac{{h^{2} }}{{b^{2} }}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{B}_{jm} \bar{W}_{2} (X_{i} ,Y_{m} ) + \left( {\frac{{\nu h^{2} }}{{a^{2} }}} \right)\mathop \sum \limits_{n = 1}^{N} B_{in} \bar{W}_{2} (X_{n} ,Y_{j} ) \\ & = - \left( {\frac{{h_{f}^{3} }}{{12(1 - \nu^{2} )b^{3} }}} \right)\mathop \sum \limits_{m = 1}^{M} \bar{C}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) - \left( {\frac{{h_{f}^{3} (2 - \nu )}}{{12(1 - \nu^{2} )a^{2} b}}} \right)\mathop \sum \limits_{n = 1}^{N} \mathop \sum \limits_{m = 1}^{M} B_{in} \bar{A}_{jm} \bar{W}_{1} (X_{n} ,Y_{m} ) \\ & \quad + \left( {\frac{{(h_{f} + h_{c} )G_{c} }}{{2E_{f} h_{c} }}} \right)\left( {\bar{V}_{1} (X_{i} ,Y_{j} ) - \bar{V}_{2} (X_{i} ,Y_{j} )} \right) \\ & \quad + \frac{{(h_{f} + h_{c} )^{2} G_{c} }}{{4E_{f} h_{c} b}}\left( {\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) + \mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} )} \right) \\ & \quad - \frac{{G_{c} h_{c} }}{{12E_{f} b}}\left( {\mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{W}_{1} (X_{i} ,Y_{m} ) - \mathop \sum \limits_{m = 1}^{M} \bar{A}_{jm} \bar{W}_{2} (X_{i} ,Y_{m} )} \right) = 0. \\ \end{aligned} $$
(75)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kamali, K., Nazemnezhad, R. & Zare, M. Interlayer effects of Van der Waals interactions on transverse vibrational behavior of bilayer graphene sheets. J Braz. Soc. Mech. Sci. Eng. 40, 54 (2018). https://doi.org/10.1007/s40430-018-0965-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-0965-3

Keywords

Search

Navigation