Skip to main content
SpringerLink
Log in

Prediction of the convective heat transfer coefficient of cutting fluid in helical drills

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

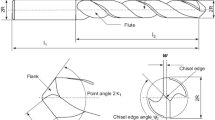
Abstract

Environmental, economical and social factors impose the elimination or reduction of the quantity of the cutting fluids used in the machining. This trend leads to a high temperature in the cutting zone. In drilling, when the cutting fluid is not supplied through the spindle, the tool tip suffers from high temperature, leading to rapid wear. In this case, the cooling of the drill tool body can contribute significantly removing the heat generated at the tool–chip interface. However, to effectively simulate the temperature at the tool tip, the effect of the cutting fluid on tool body must be known. Hence, the aim of this work was to determine the convective heat transfer coefficient of the cutting fluid on the complex body of a helical drill. In this regard, a special experimental setup is developed, allowing the drill to remain static while the coolant nozzle rotates around providing cutting fluid. A method is developed in order to determine the temperature on the drill surface as a function of the heat enters into the drill and the temperature measured at the tool base. Experiments are carried out varying coolant nozzle rotation speed and the cutting fluid flow rate. According to the results, the cutting fluid flow rate shows to have the most significant effect on the convective heat transfer coefficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Abbreviations

\(\nabla\) :

Laplace operator vector

\(A_2\) :

Contact area of the drill with the cutting fluid (m\(^2\))

\(A_\mathrm{b}\) :

Surface back area of the heating system (m\(^2\))

\(A_\mathrm{f}\) :

front surface area of the heating system (m\(^2\))

\(A_{1,3}\) :

Cross-sectional area of the drill (m\(^2\))

\(E_\mathrm{f,t,l}\) :

Insulation thickness (m)

h :

Convective heat transfer coefficient (W/m\(^2\) K)

I :

Current (A)

k :

Thermal conductivity of the tool material (W/mK)

\(k_\mathrm{i}\) :

Thermal conductivity of the insulation (W/mK)

L :

Insulation length (m)

\(l_\mathrm{f}\) :

Cutting fluid flow rate (l/h)

\(Q_\mathrm{d}\) :

Heat entering the drill (W)

\(Q_\mathrm{f}\) :

Heat removed by the cutting fluid (W)

\(Q_\mathrm{r}\) :

Heat supplied by the electric resistance (W)

\(Q_{l1 \ldots l3}\) :

Heat lost at the heating system (W)

\(R_\mathrm{n}\) :

Nozzle rotating speed (rpm)

\(R_{1 \ldots 4}\) :

Regions of the drill (rpm)

\(r_\mathrm{e,i}\) :

Insulation radius (m)

\(S_{1,2,3}\) :

Surfaces of the drill (m\(^2\))

T :

Temperature in the drill (\(^{\circ }\)C)

\(T_{1} \,\ldots\, T_{5}\) :

Temperatures inside the heating system (\(^{\circ }\)C)

\(T_\mathrm{a}\) :

Room temperature (\(^{\circ }\)C)

\(T_\mathrm{d}\) :

Temperature on the drill surface (\(^{\circ }\)C)

\(T_\mathrm{f}\) :

Cutting fluid temperature (\(^{\circ }\)C)

\(T_\mathrm{b1}\) :

Temperature on the surface \(A_3\) (\(^{\circ }\)C)

\(T_\mathrm{b2}\) :

Temperature on the back of the tool (\(^{\circ }\)C)

U :

Voltage (V)

\(\mathrm{VC}_1,2\) :

Control volume

References

  1. Sato M, Aoki T, Tanaka H, Takeda S (2013) Variation of temperature at the bottom surface of a hole during drilling and its effect on tool wear. Int J Mach Tool Manuf 68:40–47

    Article  Google Scholar 

  2. Najiha M, Rahman M (2014) A computational fluid dynamics analysis of single and three nozzles minimum quantity lubricant flow for milling. Int J Automot Mech Eng 10(1):1891–1900

    Article  Google Scholar 

  3. Obikawa T, Asano Y, Kamata Y (2009) Computer fluid dynamics analysis for efficient spraying of oil mist in finish-turning of Inconel 718. Int J Mach Tool Manuf 49(12):971–978

    Article  Google Scholar 

  4. Kurgin S, Dasch JM, Simon DL, Barber GC, Zou Q (2012) Evaluation of the convective heat transfer coefficient for minimum quantity lubrication (MQL). Ind Lubr Tribol 64(6):376–386

    Article  Google Scholar 

  5. Dhar N, Islam M, Islam S, Mithu M (2006) The influence of minimum quantity of lubrication (MQL) on cutting temperature, chip and dimensional accuracy in turning AISI-1040 steel. J Mater Process Technol 171(1):93–99

    Article  Google Scholar 

  6. Tschätsch H (2010) Applied machining technology. Springer, New York

    Google Scholar 

  7. Wakabayashi T (2010) The role of tribology in environmentally friendly MQL machining. Eng J JTEKT 1007E:2–7

  8. Karas A, Bouzit M, Belarbi M (2013) Development of a thermal model in the metal cutting process for prediction of temperature distributions at the tool–chip-workpiece interface. J Theor Appl Mech 51(3):553–567

    Google Scholar 

  9. Grzesik W, Bartoszuk M, Nieslony P (2004) Finite difference analysis of the thermal behaviour of coated tools in orthogonal cutting of steels. Int J Mach Tool Manuf 44(14):1451–1462

    Article  Google Scholar 

  10. Lazoglu I, Altintas Y (2002) Prediction of tool and chip temperature in continuous and interrupted machining. Int J Mach Tool Manuf 42(9):1011–1022

    Article  Google Scholar 

  11. Ber A, Goldblatt M (1989) The influence of temperature gradient on cutting tool’s life. CIRP Ann Manuf Technnol 38(1):69–73

    Article  Google Scholar 

  12. Debnath S, Reddy MM, Yi QS (2014) Environmental friendly cutting fluids and cooling techniques in machining: a review. J Clean Prod 83:33–47

    Article  Google Scholar 

  13. Bacci da Silva M, Wallbank J (1998) Lubrication and application method in machining. Ind Lubr Tribol 50(4):149–152

    Article  Google Scholar 

  14. Denkena B, Helmecke P, Hülsemeyer L (2014) Energy efficient machining with optimized coolant lubrication flow rates. Proc CIRP 24:25–31

    Article  Google Scholar 

  15. Jiang Z, Zhou F, Zhang H, Wang Y, Sutherland JW (2015) Optimization of machining parameters considering minimum cutting fluid consumption. J Clean Prod 108:183–191

    Article  Google Scholar 

  16. Li R, Shih AJ (2007) Tool temperature in titanium drilling. J Manuf Sci Eng 129(4):740–749

    Article  Google Scholar 

  17. Bono M, Ni J (2006) The location of the maximum temperature on the cutting edges of a drill. Int J Mach Tool Manuf 46(7):901–907

    Article  Google Scholar 

  18. Biermann D, Iovkov I (2013) Modeling and simulation of heat input in deep-hole drilling with twist drills and MQL. Proc CIRP 8:88–93

    Article  Google Scholar 

  19. Daniel CM, Rao K, Olson WW, Sutherland JW (1996) Effect of cutting fluid properties and application variables on heat transfer in turning and boring operations. In: Proceedings of the JapanUSA symposium on flexible automation, p 1119–1126

  20. Kops L, Arenson M (1999) Determination of convective cooling conditions in turning. CIRP Ann Manuf Technol 48(1):47–52

    Article  Google Scholar 

  21. Sales W, Guimaraes G, Machado A, Ezugwu E (2002) Cooling ability of cutting fluids and measurement of the chip–tool interface temperatures. Ind Lubr Tribol 54(2):57–68

    Article  Google Scholar 

  22. Luchesi VM, Coelho RT (2012) Experimental investigations of heat transfer coefficients of cutting fluids in metal cutting processes: analysis of workpiece phenomena in a given case study. P I Mech Eng B J Eng 226(7):1174–1184

    Google Scholar 

  23. Li R, Shih AJ (2007) Spiral point drill temperature and stress in high-throughput drilling of titanium. Int J Mach Tool Manuf 47(12):2005–2017

    Article  Google Scholar 

  24. Nutec Ibar Fibras Cermicas Ltda (2016) Main catalogue: blanke insulation of ceramic fiber HP, Revision 5 (In Portuguese), São Paulo

  25. Radhakrishnan T, Kawlra R, Wu S (1982) A mathematical model of the grinding wheel profile required for a specific twist drill flute. Int J Mach Tool Des Res 22(4):239–251

    Article  Google Scholar 

  26. Bergman TL, Incropera FP, DeWitt DP, Lavine AS (2011) Fundamentals of heat and mass transfer. Wiley, Amsterdam

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Santa Catarina State University, Campus Universitario, Joinville, 89219-710, Brazil

    Douglas Wellington Pontes, Joel Martins Crichigno Filho & Paulo Sérgio Berving Zdanski

Authors
  1. Douglas Wellington Pontes
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joel Martins Crichigno Filho
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Paulo Sérgio Berving Zdanski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Joel Martins Crichigno Filho.

Additional information

Technical Editor: Márcio Bacci da Silva.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pontes, D.W., Crichigno Filho, J.M. & Zdanski, P.S.B. Prediction of the convective heat transfer coefficient of cutting fluid in helical drills. J Braz. Soc. Mech. Sci. Eng. 39, 5195–5204 (2017). https://doi.org/10.1007/s40430-017-0904-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40430-017-0904-8

Keywords

Search

Navigation