Skip to main content
SpringerLink
Log in

Numerical study of the influence of the pivot position on the steady-state behavior of tilting-pad thrust bearings

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

The coordinates of the pivot pads variation of a hydrodynamic thrust bearing can result in hydrodynamic pressure field changes that forms on the surface of the pad with consequent changes in the values of the bearing performance parameters, such as power loss, load capacity and operating temperatures. The analysis was performed by computer simulation (FORTRAN), based on the numerical solution of the two-dimensional isoviscous Reynolds equation in polar coordinates by finite difference method. The simulated bearing was based on the dimensions of a KV 9 Kingsbury thrust bearing, existing on the tribology laboratory of the university. With the pivot position variation (radius r and angle θ), starting with a bearing with central pivot pads, as well as a bearing consisting of pads with pivot located in other positions, both in the radial direction and in the circumferential direction, was possible to verify some significant changes in the bearing performance parameters. It was found that the maximum load occurs in the case of pads with pivot located approximately 60% of the average circumferential length, but for a substantially longer than the average radius of radial position. On the other hand, the minimum power loss occurs due to friction in the bearings for pivoting the pads with about 67% of the average circumferential length thereof.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

a :

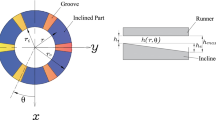
Oil film thickness obtained with the inclination of r axes

A1, A2, A3, A4 and A5:

Coefficients from discretized Reynolds equation

b :

Oil film thickness obtained with the inclination of θ axes

c p :

Specific heat of lubricant

denom:

Term used in the denominator from A1, A2, A3, A4 and A5 coefficients

DIFR:

Difference between the previously and currently iteration of the radial pivot position

DIFTETA:

Difference between the previously and currently iteration of the angular pivot position

fT :

Temperature coefficient

F :

Dimensionless load capacity of a pad

F a :

Friction force

F 0 :

Dimensional load capacity of a pad

h :

Oil film thickness at any point over the pad surface

h 0 :

Dimensional oil film thickness

h p :

Oil film thickness at the pivot position

h rs :

Oil film thickness at the intersection of the trailing edge of the pad with the θ axes

H :

Dimensionless power loss in a pad

H 0 :

Dimensional power loss in a pad

H 1 and H 2 :

Dimensionless discrete components from dimensional power loss equation

i :

Discrete variable in the θ direction

j :

Discrete variable in the r direction

J :

Thermal equivalent of work (4186 J/kcal)

k :

Number of iterations

k 1 and k 2 :

Walther’s equation constants

K :

Ratio of the values of h rs and h p

L :

Pad width

m :

Number of points in the r direction

m p :

Number of intervals in the r direction

n :

Number of points in the θ direction

n p :

Number of intervals in the θ direction

N :

Rotational speed

p :

Dimensionless pressure

pn :

Dimensionless pressure in the current interaction

p 0 :

Dimensional pressure

P m :

Average pad pressure

q E :

Dimensionless component from inlet circumferential flow equation

\(q_{{R_{\text{e}} }}\) :

Dimensionless lateral flow in outer radius

\(q_{{R_{\text{i}} }}\) :

Dimensionless lateral flow in inner radius

q S :

Dimensionless component from outlet circumferential flow equation

q 0E :

Component in brackets from Eq. (26)

Q E :

Inlet oil flow rate

\(Q_{{LR_{\text{e}} }}\) :

Outer radius oil flow rate

\(Q_{{LR_{\text{i}} }}\) :

Inner radius oil flow rate

Q S :

Outlet oil flow rate

Q sup :

Lubricant supply flow rate

r :

Radial coordinate

r 0 :

Dimensional radius

r 0p :

Radial coordinate of pivot position and polar coordinate of the resultant force F 0

R e :

Outer radius of the pad

R i :

Inner radius of the pad

T e :

Lubricant inlet temperature in the pad

T ef :

Effective temperature

T m :

Lubricant average temperature

T mist :

Temperature of the mixture

T 0 :

Dimensional lubricant temperature in the pad

T s :

Lubricant outlet temperature in the pad

T sup :

Lubricant supply temperature

U :

Tangential velocity in the rotating collar

x :

Cartesian coordinate of the pivot position

x i :

Cartesian coordinate of the sector shaped infinitesimal element

x p :

Cartesian coordinate of the resultant force F 0

y :

Cartesian coordinate of the pivot position

y i :

Cartesian coordinate of the sector shaped infinitesimal element

y p :

Cartesian coordinate of the resultant force F 0

Z :

Number of pads

α r :

Angle of inclination around of θ axes

α θ :

Angle of inclination around of r axes

Δθ :

Pad angle divided by number of intervals in the θ direction

Δr :

Pad width divided by number of intervals in the r direction

ΔT :

Lubricant temperature rise in a pad

η :

Lubricant dynamic viscosity

θ :

Angular coordinate

θ 0 :

Pad angle

θ p :

Angular coordinate of pivot position and polar coordinate of the resultant force F 0

λ :

Coefficient from the coefficient of over-relaxation great equation

λ 0 :

Coefficient of over-relaxation great

ρ :

Lubricant density

References

  1. Frene J, Nicolas D, Degueurce B, Berthe D, Godet M (1997) Hydrodynamic lubrication—bearings e thrust bearings. Elsevier, Amsterdam

    MATH  Google Scholar 

  2. Gardner WW (1987) Tilting pad thrust bearings tests—influence of three design variables. In: Dowson D, Taylor CM, Godet M, Berthe D (eds) Fluid film lubrication—Osbourne Reynolds Centenary. Elsevier, Amsterdam, pp 113–120

    Google Scholar 

  3. Gardner WW (1988) Tilting pad thrust bearing tests—influence of pivot location. Trans ASME J Tribol 110:609–613

    Article  Google Scholar 

  4. Raimondi AA, Boyd J (1955) Applying bearing theory to the analysis and design of pad-type bearings. Trans ASME J Tribol 77:287–309

    Google Scholar 

  5. Pinkus O (1958) Solution of the tapered-land sector thrust bearing. Trans ASME J Tribol 80:1510–1516

    Google Scholar 

  6. Tieu AK (1991) Hydrodynamic thrust bearing: theory and experiment. Trans ASME J Tribol 113:633–638

    Article  Google Scholar 

  7. Almqvist T, Glavatskikh SB, Larsson R (2000) THD analysis of tilting pad thrust bearings—comparison between theory and experiments. Trans ASME J Tribol 122:412–417

    Article  Google Scholar 

  8. Pinkus O, Sternlicht B (1961) Theory of hydrodynamic lubrication. McGraw-Hill, New York

    MATH  Google Scholar 

  9. Huebner KH (1974) Application of finite element methods to thermohydrodynamic lubrication. Int J Numer Methods Eng 8:139–165

    Article  MATH  Google Scholar 

  10. Markin D, McCarthy DMC, Glavatskih SB (2003) A FEM approach to simulation of tilting-pad thrust bearing assemblies. Tribol Int 36:807–814

    Article  Google Scholar 

  11. Schwarz VA, Silva PF, Vicente WM, Dias JC, Kuhn MJ (2003) Effects of the pivot position and lubricant flow rate on the behavior of sector shaped tilting pads hydrodynamic thrust bearings. In: International Congress of Mechanical Engineering (COBEM), 2003. 17th International Congress in São Paulo-Brazil, pp 1–9

  12. Galvão MM (2006) Analysis of the operational behavior of sector shaped tilting pad hydrodynamic thrust bearing. Dissertation, Federal University of Itajubá (in Portuguese)

  13. Ferziger JH (1981) Numerical methods for engineering application. Wiley, New York

    MATH  Google Scholar 

  14. Silva PF (1993) Predictive analysis of the operational behavior of hydrodynamic radial bearing. Dissertation, Federal University of Itajubá (in Portuguese)

  15. Michell AGM (1905) The lubrication of plane surfaces. Zeitschrift für Mathematik u. Physik 52:123–137

    MATH  Google Scholar 

  16. Cameron A (1966) The principles of lubrication. Longmans, London

    Google Scholar 

  17. Raimondi AA, Boyd J (1958) A solution for the finite journal bearing and its application to analysis and design, part 1, 2 and 3. Trans ASME 1:159–209

    Google Scholar 

  18. Swift HW (1937) Theory and experiment applied to journal bearing design. Proc IME Gen Discuss Lubr Lubr 1:309–316

    Google Scholar 

  19. Glavatskih SB, DeCamillo S (2004) Influence of oil viscosity grade on thrust pad operation. J Eng Tribol Proc Inst Mech Eng Part J 218:401–412

    Article  Google Scholar 

  20. Stachowiak GW, Batchelor AW (2005) Engineering tribology. Elsevier Butterworth Heinemann, Oxford

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Federal University of Itajubá-UNIFEI, Av.BPS, no 1303, Pinheirinho, Itajubá, Minas Gerais, 37500-903, Brazil

    Marcos Moura Galvão, Genésio José Menon & Vilmar Arthur Schwarz

Authors
  1. Marcos Moura Galvão
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Genésio José Menon
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Vilmar Arthur Schwarz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marcos Moura Galvão.

Additional information

Technical Editor: Fernando Antonio Forcellini.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Galvão, M.M., Menon, G.J. & Schwarz, V.A. Numerical study of the influence of the pivot position on the steady-state behavior of tilting-pad thrust bearings. J Braz. Soc. Mech. Sci. Eng. 39, 3165–3180 (2017). https://doi.org/10.1007/s40430-017-0805-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40430-017-0805-x

Keywords

Search

Navigation