An evolutionary model of bi-flux diffusion processes

Abstract

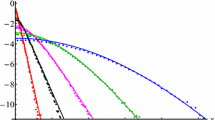
In previous papers, we presented a new theory of bi-flux diffusion processes. The bi-flux consists of the simultaneous flux of two sets of particles scattering with two distinct velocities. The first set obeys the classical Fick’s law, it is the primary flux. The complementary set follows a new law, it is the secondary flux. The primary and secondary fluxes are excited into two distinct energy states. The fundamental energy source for the primary flux is the translational energy or active energy. For the secondary flux, linear and angular momentum, both, contribute to the excitation state. Two cases are analyzed. The first one refers to an isolated system in a particular phase state S₁ where active energy decreases continuously. The system tends to an energy state where active energy is absent. In the second case, the system is in a different phase state S₂ where active energy increases continuously. The system recovers active energy and tends to a pure Fickian diffusion process. In both processes, the fractions representing the density distribution functions for the primary and secondary fluxes vary with time. It is remarkable that the fourth order equation provides a consistent approach to take into account the rotational energy which otherwise would not be possible with the classical theory. A particular law for the variation of the fraction of particles following Fick’s law is derived. A notion of entropy related to the particular energy states is introduced. Selected examples are presented showing the concentration profile evolution for different rates of energy transfer.

Appendix

The present theory may be extended to simulate the dynamics of an arbitrary number of microstates. Clearly a real process could be better simulated by a multi-flux diffusion phenomenon since particles flow with different velocities. It is expected that, even if initially there is only one prevailing flux, after a short time the single-flux breaking effect phenomenon will raise an enormous number of microstates. That is, the model closer to the possible real case must be generalized as to include several partitions consisting of set of particles in different excitation states. Thus assuming m nested excitation states {E ₁, E ₂, … E _m } let β _i be the fraction of mass belonging to the excitation state E _i . Since all the particles in the system must be in some excitation state it is necessary that $\beta_{1} + \beta_{2} + \cdots + \beta_{n} = 1$. The governing equation for this case, assuming that the diffusion occurs in an isotropic medium, reads [3].

$$\frac{\partial q} {\partial t} + \sum^{m}_{n=1} (- 1)^n\beta_{1} \beta_{2} \ldots \beta_{n} D_{n}\frac{\partial^{2n} q}{\partial x^{2n}} = 0$$

(7)

The fluxes are given by:

$${\varvec{\Psi}}_{n} = \left( { - 1^{n} } \right)\beta_{1} \beta_{2} \ldots \beta_{n - 1} D_{n} \frac{{\partial^{2n - 1} q}}{{\partial x^{2n - 1} }}{\text{e}}_{1}\,\,\, {\text{with}}\quad n = 1, \ldots ,m$$

(8)

Again Ψ ₁ is the primary flux while Ψ _n (n > 1) are subsidiary fluxes consisting of nested states such that the state n + 1 exists if and only if the state n also exists. The coefficient D ₁ is the well-known diffusion coefficient and D _n (n > 1) are the reactivity coefficients. The problem now is that we lack the determination of the reactivity coefficients D _n and the partitions coefficients β _n besides treatable mathematical tools to perform a sufficiently detailed analysis of Eq. (7).The theory introduced in the previous sections assumes a drastic simplification reducing the system to two representative states Ψ ₁ and Ψ ₂ where the first correspond to the fundamental primary state and the second represents the average of the possible subsidiary states. Though this approach reducing the phenomenon to a bi-flux process, or equivalently to a dual energy excitation state represents a considerable simplification it is a second order approximation of the real phenomenon. Indeed the classical approach considers just a single class of random motion representing the scattering of particles in some supporting medium. Several works have been devoted to the diffusion process considered as the result of the Brownian motion of a very large number of particles where the relevant energy state may be associated to the kinetic energy generated by the linear momentum of all particles. The angular momentum is ignored. But as we have shown if the angular momentum plays a significant role the process than the system may be turn to be considerable complex. The system of Eqs. (7) and (8) may be considered the analytical equivalent of statistical mechanics.