Underground current impulses as a possible source of unipolar magnetic pulses

Abstract

Recently several cases of observations of unipolar magnetic field pulses associated with earthquakes at different points (California, Italy, Peru) have been recorded. The paper attempts to model unipolar magnetic field pulses based on one mechanism that should be omnipresent for all measurement points, namely, the magnetic field diffusion through a conductive medium. The structure of magnetic fields supported by electric current sources is thoroughly modelled. The source of electric current is considered as an elongated volume of finite cross-section being immersed in a conductive medium. To model the unipolarity feature of the observed pulses prior to and at the earthquake main shock, the electric current of the source is of impulse form. Special attention is paid to the differences in the pulse structure (as amplitude envelope and the pulse width) that are measured by various magnetometers (fluxgate or search-coil). An analysis and comparison with recorded magnetic field pulse characteristics reveal that the observed unipolar pulses may have a common genesis, an electric current source within a conductive medium such as the earth crust.

Appendices

Appendix 1

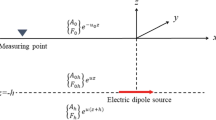
The distance r between the measurement point r(x, y) and the axis of the source electric current [placed at point (x  = 0, y  = 0)] may exceed the cross section parameters x₀ and y₀ (r  ≫  x₀ or y₀). If x₀ (or y₀)  ≫  y₀ (or x₀), a strip current geometry (fault-like plane) is formed. Otherwise, if the cross section parameters are of comparable size, i.e. x₀ ≈ y₀, and the distance r(x,y) exceeds x₀, y₀, the error function in expressions (5a) may be safely approximated by:

$$ {\text{erf}}\left( {u \pm \delta u} \right) \approx {\text{erf}}\left( u \right) { \exp }\left( { - u^{2} } \right)\delta u $$

(9)

where u is the function argument: u is equal to $\frac{{\widetilde{x}}}{{2\sqrt {\widetilde{t}} }}$ or $\frac{{\widetilde{y}}}{{2\sqrt {\widetilde{t}} }}$; $u$ is equal to $\frac{{\widetilde{x}_{0} }}{{\sqrt {\widetilde{t}} }}$ or $\frac{{\widetilde{y}_{0} }}{{\sqrt {\widetilde{t}} }}$, respectively. The final expressions are:

$$ B_{x} = \frac{2}{\pi }\frac{{\mu_{0}^{2} \sigma j_{0} x_{0} R^{2} }}{t}sh\left( {\frac{{\widetilde{y} y_{0} }}{{2\widetilde{t}\sqrt S }}} \right){ \exp }\left( { - \frac{{\widetilde{x}^{2} + \widetilde{y}^{2} }}{{4\widetilde{t}}}} \right) $$

(10a)

$$ B_{y} = \frac{2}{\pi }\frac{{\mu_{0}^{2} \sigma j_{0} y_{0} R^{2} }}{t}sh\left( {\frac{{\widetilde{x}x_{0} }}{{2\widetilde{t}\sqrt S }}} \right){ \exp }\left( { - \frac{{\widetilde{x}^{2} + \widetilde{y}^{2} }}{{4\widetilde{t}}}} \right) $$

(10b)

Let us introduce a diffusion time scale of medium conductivity σ: τ_d ≡ $\mu_{0} \sigma r^{2}$, where r ≡ $\sqrt {(x^{2} + y^{2} }$. Let us denote $j_{0} \left( {2x_{0} } \right)\left( {2y_{0} } \right)$ as I₀ (the current source strength). Further, I₀ is considered constant irrespectively of the magnitudes of the actual cross-section parameters $(x_{0} , y_{0} )$. Then the magnetic field component B_x varies as:

$$ B_{x} = \frac{1}{2\pi }\left( {\frac{{\mu_{0} I_{0} \tau }}{{ty_{0} }}} \right)sh\left( {\frac{{\widetilde{y} y_{0} }}{{2\widetilde{t}r}}} \right){ \exp }\left( { - \frac{{\widetilde{r}^{2} }}{{4\widetilde{t}}}} \right) $$

(11)

The magnetic field expression (when x₀/y₀ ≈1) may be applied to a square or cylindrical (tube) current geometry of radius x_o ≈ y_o. In that case, the azimuthal magnetic field component B_φ, supported by a current of cylindrical cross section of radius R will be expressed by (11).

Let us now consider a strip current of width 2yo and infinite length along the x axis (x₀ → ∞). The electric current density $\vec{j}$ ₀ is parallel to the z-axis. Then:

$$ B_{x} \left( y \right) = \frac{2}{\sqrt \pi }\left( {\frac{{\mu_{0} j_{0} y}}{{\sqrt {\widetilde{t}} }}} \right)sh\left( {\frac{{\widetilde{y} y_{0} }}{{2\widetilde{t}y}}} \right)\exp \left( { - \frac{{\widetilde{y}^{2} }}{{4\widetilde{t}}}} \right) $$

(12)

where y is the distance to the middle plane (defined as y = 0) of the strip current. This expression yields the magnetic field produced by electric current density $j_{0}$ along the z axis permeating an infinite strip current of thickness 2y₀.

The strip current model may have various applications in geo-electromagnetism. One of them is electric currents that are released in soil through the earthing systems (this occurs mainly in a shallow layer of some depth of higher conductivity). Other strip (or layer) structures of high conductivity (σ ≈ 10⁻¹ ÷ 4 S/m) are the fault, water basin systems (river, lake, sea, ocean), where electric currents (induced mainly by global geomagnetic activity) may be concentrated.

Expressions (3) describe the magnetic field variations in space and time produced by transient electric currents of finite extension (along x and y). Naturally, these general expressions should be consistent with the expression of the magnetic field produced by a line current impulse. These expressions should also represent a generalization of the well-known formula of the magnetic field produced by a line current in static approximation (t → ∞).

First, let us check the validity of (11) at the limit ($y_{0} \to 0$ and $x_{0} \to 0$). Applying the L’Hôspital rule to expression (10a), from straightforward algebra one gets:

$$ B_{line,tr} = \frac{1}{4\pi }\frac{{\mu_{0} I_{0} }}{r}\frac{1}{{\widetilde{t}^{2} }}{ \exp }\left( { - \frac{{\widetilde{r}^{2} }}{{4\widetilde{t}}}} \right) $$

(13)

where B_x is now replaced by the symbol $B_{line,tr}$ and the coordinate y - by r. Further, when there is a constant current source, e.g. switched on at time t = 0, the current source ~ δ(t) in (1) should be replaced by the Heaviside’s function θ(t). Then, the magnetic field at moment t will be simply derived by integration over $\widetilde{t}$:

$$ B_{line} = \frac{1}{2\pi }\frac{{\mu_{0} I_{0} }}{r}\exp \left( { - \frac{{r^{2} \mu_{0} \sigma }}{4t}} \right) $$

(14)

For t → ∞, expression (14) expectedly reduces to:

$$ B_{line,st} \to \frac{{\mu_{0} I_{0} }}{2\pi r} $$

(15)

which is identical to the magnetic field that is circumferential to an infinite wire carrying a current of strength I_o.Attention should be paid to the ratio B_line,tr/B_line,st and its time profile. At its maximum (when t = t_peak = τ_d/8), this ratio becomes equal to ~ 4.5. This suggests that at the given measurement point the transient magnetic signal emerges with greater amplitude (4.5 times) compared to that produced by same current strength under static conditions.

Appendix 2

In fact, unipolar pulses have been recorded by several kinds of magnetometers, among them fluxgate and search-coils magnetometers. Fluxgate magnetometers are designed to measure DC fields, while the searchcoil - AC fields. Concretely, the search-coil sensor is built on the induction principle. The induced voltage, say $\epsilon$, is proportional to the time derivative of the magnetic flux as follows from the Faraday’s law, i.e.

$$ \epsilon = -\, {\text{n}}S\frac{{{\text{d}}B}}{{{\text{d}}t}} $$

(16)

where S is the cross-section and n is the number of turns in the sensor coil. The coil sensor is characterized by self-inductance L. It also features resistance R and capacitance C. Generally speaking, the transfer function between the output (the measurable voltage, V_out) and the flux density (the magnetic field, B) of the induction sensor depends on both the resonance frequency ω_r (equal to 1/sqrt(LC) and the RC constant. However, their effects should be negligible under low-frequency conditions: ω ≪ ω_r and ω ≪ 1/RC (fulfilled for frequencies below 1 Hz, the fluxgate sampling frequency). This condition is practically satisfied when the frequency is less than 10–100 Hz. Note that the unipolar pulses observed by fluxgate magnetometers (of sampling frequency of 1 Hz) are well below this upper limit.

Examining unipolar magnetic pulses recorded by fluxgate magnetometers under these low-frequency conditions, the validity of Eq. (16) is confirmed.