Diameter of Compact Riemann Surfaces

Abstract

Diameter is one of the most basic properties of a geometric object, while Riemann surfaces are one of the most basic geometric objects. Surprisingly, the diameter of compact Riemann surfaces is known exactly only for the sphere and the torus. For higher genuses, only very general but loose upper and lower bounds are available. The problem of calculating the diameter exactly has been intractable since there is no simple expression for the distance between a pair of points on a high-genus surface. Here we prove that the diameters of a class of simple Riemann surfaces known as generalized Bolza surfaces of any genus greater than 1 are equal to the radii of their fundamental polygons. This is the first exact result for the diameter of a compact hyperbolic manifold.

1 Introduction

A Riemann surface is any connected, one-dimensional complex manifold. According to the classification theorem of closed surfaces [1], any compact Riemann surface is homeomorphic to either the sphere or the connected sum of g tori, where g is the genus of the surface. Once equipped with a metric, a Riemann surface becomes a Riemannian manifold. The sphere $(g = 0)$ admits the spherical metric, the torus $(g = 1)$ admits the Euclidean metric, while the surfaces of genus $g > 1$ admit the hyperbolic metric.

The diameter $\mathscr {D}$ of a metric space is the maximum distance between a pair of points in it. Diameter is one of the most basic characteristics of any geometric object. Surprisingly, the diameter of compact Riemann surfaces is known exactly only for the sphere and the torus. The best results on the diameter of surfaces of genus $g > 1$ are only loose lower and upper bounds in terms of the total surface area, the systole, and the genus [2,3,4,5]. The systole is the length of a shortest non-contractible loop on the surface.

Our main result is a proof of the following theorem:

Theorem 1

The diameter of a class of Riemann surfaces $S_g$, known as generalized Bolza surfaces, of genus $g > 1$ is $\mathscr {D}_g = \text {arccosh}\left( \cot ^2(\pi /(4g))\right)$.

The definition of the surfaces $S_g$ is in the next section. In particular, $S_2$ is known as the Bolza surface [6], one of the first compact hyperbolic manifolds ever considered. A free particle moving along a geodesic on the Bolza surface was the first dynamical system proven rigorously to be chaotic [7]. The Bolza surface is also known to maximize the systole across all genus-2 surfaces [8]. For ${g>2}$, the $S_g$ are the generalized Bolza surfaces [9]. They appear frequently in studies of hyperbolic surfaces due to their high degree of symmetry [9,10,11,12].

Knowing the diameter of a surface, we can efficiently compute the distance between any pair of points on it, a result to be published elsewhere. Theorem 1 states that the Bolza surface has diameter $\mathscr {D} = \textrm{arccosh}(3+2\sqrt{2}) \approx 2.45$. To the best of our knowledge, this is the first ever exact result for the diameter of a compact hyperbolic manifold. The closest results to ours appear to be the ones in [13]. They apply to manifolds of dimension at least five.

We proceed by collecting all the necessary background information and definitions in Sect. 2. Section 3 contains the outline of the proof of Theorem 1 split into a sequence of theorems that we state in that section as well. We prove all those theorems in the concluding Sect. 4.

2 Background Information and Definitions

We use the Poincaré disk model of the hyperbolic plane $\mathbb {H}^2$. The isometries (distance-preserving maps) of $\mathbb {H}^2$ are given by the matrices

$$\begin{aligned} \left[ \begin{matrix} a &{} \overline{c} \\ c &{} \overline{a} \end{matrix} \right] , \quad a,c \in \mathbb {C}, ~ |a |^2 - |c |^2 = 1, \end{aligned}$$

(1)

which form a subgroup of $PSL(2, \mathbb {C})$, the invertible ${2 \times 2}$ complex matrices. The action of each matrix on a complex number z in the Poincaré disk ${\mathbb {D} = \{ z \in \mathbb {C}: |z |< 1\}}$ is a fractional linear transformation:

$$\begin{aligned} \left[ \begin{matrix} a &{} \overline{c} \\ c &{} \overline{a} \end{matrix} \right] (z) = \frac{az + \overline{c}}{cz + \overline{a}}. \end{aligned}$$

(2)

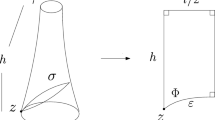
A Fuchsian group $\mathscr {F}$ is a discrete subgroup of ${PSL(2,\mathbb {C})}$ that has an invariant disk in ${\mathbb {C}^\infty }$. Each $\mathscr {F}$ defines a hyperbolic Riemann surface S which is the quotient surface ${ S = \mathbb {H}^2/\mathscr {F} }$. A fundamental domain is an open, connected set in ${\mathbb {H}^2}$ that contains at most one representative of each point on S, and whose closure contains at least one representative of each point on S [14]. A fundamental domain and its images under the actions of $\mathscr {F}$ tessellate $\mathbb {H}^2$.

Since points on a quotient surface S are cosets in $\mathbb {H}^2/\mathscr {F}$, the distance between two points (cosets) $[z] = \mathscr {F} z, [w] = \mathscr {F} w$ on S is given by

$$\begin{aligned} \delta ^\star ([z], [w]) = \inf \{ \delta (z^\prime , w^\prime ), z^\prime \in [z], w^\prime \in [w] \} , \end{aligned}$$

(3)

where $\delta (z, w)$ denotes the distance in $\mathbb {H}^2$. The diameter $\mathscr {D}$ of S is the largest distance between two points on S.

The best results on the diameters of Riemann surfaces of genus $g > 1$ are as follows. It was shown in [2] that for any such surface, the following inequalities hold, where $\ell$ is the systole, A is the total area of the surface, and $\mathscr {D}$ is the diameter:

$$\begin{aligned} 2 \ell \sinh (\mathscr {D})&\ge A \text {, and } \end{aligned}$$

(4)

$$\begin{aligned} 2 \sinh \!\left( \frac{\ell }{4}\right) \mathscr {D}&\le A . \end{aligned}$$

(5)

In [3] it was shown that

$$\begin{aligned} 4 \cosh \!\left( \frac{\ell }{2}\right) \le 3 \cosh (\mathscr {D}) - 1 . \end{aligned}$$

(6)

Another lower bound exists in terms of the area alone [4]:

$$\begin{aligned} \cosh \mathscr {D} \ge \frac{A}{2 \pi } + 1 , \end{aligned}$$

(7)

and finally, there is the following lower bound in terms of the genus [5]:

$$\begin{aligned} \cosh \mathscr {D} \ge \frac{1}{\sqrt{3}} \cot \left( \frac{\pi }{6(2g-1)} \right) . \end{aligned}$$

(8)

All of the bounds above hold in general for any Riemann surface, as do other related spectral results [15,16,17]. However, none of them is tight for the ${S_g}$.

Fig. 1

Left: The Bolza surface $(S_2)$ and its “gluing” scheme. Sides that are identified in the quotient space are labeled with the same color, and the arrows represent the actions of the generators ${ \{t_k\} }$ and their inverses on the fundamental polygon. Right: $S_3$ and its gluing scheme

The generalized Bolza surface ${S_g}$ of genus g is defined [9, 18] to be the surface obtained by identifying (“gluing”) the opposite sides of the regular 4g-gon with interior angles $\pi /(2g)$, Fig. 1, whose side length s and radius R satisfy [18]

$$\begin{aligned} \cosh ^2 \left( \frac{s}{2} \right) = \cosh R = \cot ^2 \left( \frac{\pi }{4g} \right) , \end{aligned}$$

(9)

and whose vertices $\{ v_k \}$ are evenly spaced at distance R from the origin:

$$\begin{aligned} v_k = \tanh \!\left( \frac{R}{2}\right) ~ e^{\left( k - 1/2 \right) \pi i/(2g)} , \quad k = 0,1, \dots , 4g - 1 . \end{aligned}$$

(10)

This surface $S_g$ is the quotient surface ${\mathbb {H}^2 / \mathscr {F}_g}$, where ${\mathscr {F}_g}$ is the Fuchsian group generated by the following 2g generators and their inverses:

$$\begin{aligned} t_k = \left[ \begin{matrix} 1 &{} \tanh \left( \frac{s}{2} \right) e^{k \pi i/(2g)} \\ \tanh \left( \frac{s}{2} \right) e^{- k \pi i/(2g)} &{} 1\end{matrix} \right] , \quad k = 0,1, \dots , 2g - 1. \end{aligned}$$

(11)

These generators glue the opposite sides of the polygon by mapping it to its edge-adjacent polygons in the tessellation as shown in Fig. 1. By Poincaré’s theorem [14], the interior of the polygon is a fundamental domain of ${S_g}$, while the polygon itself is called the fundamental polygon.

The surface $S_2$ of genus 2 is the well-known Bolza surface [6]. The surfaces ${S_g}$ are also known as the Wiman surfaces of type II [11, 12]. They have 8g automorphisms, except the ${g=2}$ Bolza surface, which has 48 automorphisms. The ${S_g}$ also have automorphisms of order 4g, which is the second largest possible order, as was proven in [10].

Our main result is the exact diameter of the surface ${S_g}$ of genus ${g > 1}$, Theorem 1, which in view of Eq. (9) can be restated as:

Theorem 1

${\mathscr {D}_g = R}$.

The problem of finding the diameter is not trivial thanks to the definition of the distance in Eq. (3), which is an infimum over the infinitely many elements in ${\mathscr {F}_g}$. Even though this infimum is actually a minimum since only a finite subset of group elements needs to be considered, there is no explicit expression for such a subset, which is the main difficulty in the problem. In fact, as mentioned in the introduction, our main motivation for this paper is that the knowledge of the diameter of a surface allows us to provide an explicit expression for this subset, leading to an efficient formula to compute distances between pairs of points on the surface, a result to appear in a follow-on paper.

Our proof of the main result, which we outline in the following section, is a combination of geometric and algebraic techniques. Specifically, we use some geometric symmetries of $S_g$ to simplify the problem, and algebra to compute the optimal distances.

3 Proof Strategy

We first observe that every vertex of the fundamental polygon represents the same point in the quotient space; we will call this point the quotient vertex, $[v] \in S_g$. Similarly, we define [0] as the point in the quotient space to which the origin maps. For an arbitrary point z in the Poincaré disk, let $d_0(z)$ and $d_v(z)$ denote the quotient distances from [z] to [0] and [v], respectively.

The proof of Theorem 1 will be broken into several smaller, sequential theorems. First, we will show that ${\delta ^\star ([0],[v]) = R}$, thus proving the following theorem:

Theorem 2

The diameter $\mathscr {D}_g$ of $S_g$ is at least R, $\mathscr {D}_g \ge R$.

The remaining theorems are aimed at proving $\mathscr {D}_g \le R$, or equivalently, ${\delta ^\star ([z],[w]) \le R}$ for every pair of points [z], [w] in the quotient space. The symmetry of $S_g$ allows us to make several simplifying assumptions about [z] and [w] without loss of generality.

The symmetries of the quotient surface $S_g$ are isometric bijections that map ${S_g}$ to itself. In the Poincaré disk ${\mathbb {D}}$, these symmetries can be thought of as the subgroup of isometries $\phi$ of ${\mathbb {D}}$ for which the projection ${\phi ^\star }$ of ${\phi }$ onto the quotient surface, given by

$$\begin{aligned} \phi ^\star ([p]) = [\phi (p)] , \end{aligned}$$

(12)

is well-defined and isometric. These properties are satisfied by all ${\phi }$ for which the Fuchsian group ${\mathscr {F}_g}$, a subgroup of ${PSL(2,\mathbb {C})}$, is invariant under conjugation by ${\phi }$: ${\phi \mathscr {F}_g \phi ^{-1} = \mathscr {F}_g}$. Indeed, for such ${\phi }$ and any ${f,f_1,f_2 \in \mathscr {F}_g}$ and ${p,p_1,p_2 \in \mathbb {D}}$, there exist ${f^\prime ,f_1^\prime ,f_2^\prime \in \mathscr {F}_g}$ such that

$$\begin{aligned}&\phi ^\star ([fp]) = [\phi f(p)] = [f^\prime \phi (p)] = [\phi (p)] = \phi ^\star ([p]), \text { and} \end{aligned}$$

(13)

$$\begin{aligned}&\delta ^*(\phi ^*([p_1]),\phi ^*([p_2])) = \delta ^*([\phi (p_1)], [\phi (p_2)]) \nonumber \\&\quad = \min \{ \delta (f_1 \phi (p_1),f_2 \phi (p_2)), f_1,f_2 \in \mathscr {F}_g \} \nonumber \\&\quad = \min \{ \delta (\phi f_1^\prime (p_1),\phi f_2^\prime (p_2)), f_1^\prime ,f_2^\prime \in \mathscr {F}_g \} \nonumber \\&\quad = \min \{ \delta (f_1^\prime (p_1)), \delta (f_2^\prime (p_2)), f_1^\prime ,f_2^\prime \in \mathscr {F}_g \} \nonumber \\&\quad = \delta ^\star ([p_1],[p_2]), \end{aligned}$$

(14)

so ${\phi }$ is well-defined and an isometry.

The simplest such isometries are the elements of $\mathscr {F}_g$. Indeed, for ${\phi \in \mathscr {F}_g}$ we have ${\phi \mathscr {F}_g \phi ^{-1} = \mathscr {F}_g}$. In this case, ${\phi ^\star }$ is simply the identity function on ${S_g}$. Therefore, $S_g$ is symmetric under actions by elements of ${\mathscr {F}_g}$.

Another subgroup of isometries of $\mathbb {D}$ that are symmetries of $S_g$ are rotations of $\mathbb {D}$ by ${\pi / (4g)}$. Although this fact is evident from the definition of $S_g$ in Sect. 2, we give its formal proof in Sect. 4.

Fig. 2

The dual tessellation (blue) overlayed against the original tessellation (black) in the case $g = 2$

The final and most complicated subgroup of symmetries of $S_g$ that we will need is its dual symmetries. We define them with the aid of new fundamental polygons that we call the dual polygons, and the corresponding dual tessellation of $\mathbb {H}^2$. Dual polygons are formed by joining by geodesics the centers of the 4g polygons around the vertices in the original tessellation, Fig. 2. We will prove the following proposition:

Proposition 1

Let ${\phi }$ be any isometry of $\mathbb {D}$ that maps the fundamental polygon to any of its dual polygons. Then the projection $\phi ^\star : S_g \rightarrow S_g$ given by

$$\begin{aligned} \phi ^\star ([z]) = [\phi (z)] \end{aligned}$$

(15)

is well-defined and is an isometric automorphism of $S_g$. In particular, dual polygons are fundamental polygons.

The rotational and dual symmetries of $S_g$ allow us to reduce drastically the set of all the possibilities of where the pairs of points z and w can lie to the following subset:

Proposition 2

To prove Theorem 1, it suffices to consider only the pairs of points z and w satisfying the following conditions:

• 1. z lies in triangle ${T = \Delta 0 v_1 v_2}$, Fig. 3,

• 2. $d_0(z) \ge d_v(w)$,

• 3. $d_v(w) \le s/2$.

Assuming, thanks to Prop. 2, that the first point z lies in the triangle T with vertices $O,v_1,v_2$, let ${w_1,w_2 \in [w]}$ be the two dual-tessellation representatives of [w] lying in the two dual polygons centered at $v_1,v_2$, respectively, Fig. 3. To prove our desired result ${\delta ^\star ([z],[w]) \le R}$, it suffices to show that

$$\begin{aligned} \min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R , \end{aligned}$$

(16)

simply because

$$\begin{aligned} \delta ^\star ([z],[w])&= \min \{ \delta (z^\prime , w^\prime ), z^\prime \in [z], w^\prime \in [w] \} \nonumber \\&\le \min \left[ \delta (z,w_1), \delta (z,w_2) \right] . \end{aligned}$$

(17)

Fig. 3

Left: The representatives $w_1$ and $w_2$ of [w] in the dual tessellation in the ${g=2}$ case. They are images of w in the dual polygons centered at ${v_1}$ and ${v_2}$. Right: The domain $\Omega _w$ is the set of points z satisfying the conditions in Prop. 2 for a given point w

Before we prove Eq. (16) using algebra, we take one final step to reduce the number of possibilities for the locations of z, w to consider. Given w such that $d_v(w) \le s/2$, we define the domain $\Omega _w$ as the set of all $z \in T$ for which z and w meet the conditions listed in Prop. 2, Fig. 3. We will prove the following:

Theorem 3

Given w for which $d_v(w) \le s/2$, the function

$$\begin{aligned} f(z) = \min \left[ \delta (z,w_1), \delta (z,w_2) \right] \end{aligned}$$

attains its global maximum over the domain $\Omega _w$ on its boundary ${\partial \Omega _w}$.

This theorem allows us to reduce the possibilities for the location of z even further, to include only the points on the boundary of $\Omega _w$.

The final step in the proof of Theorem 1 is to show that Eq. (16) holds for all of the z, w pairs satisfying all the conditions above:

Theorem 4

Given w for which $d_v(w) \le s/2$, for all $z \in \partial \Omega _w$ we have

$$\begin{aligned} \min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R . \end{aligned}$$

Thus we will have shown that $\mathscr {D}_g \le R$, and the combination of this result with that of Theorem 2 proves Theorem 1.

One important question is how generalizable our proof strategy outlined in this section is to other surfaces, such as those appearing in the Poincaré theorem [19] or the canonical surfaces [20]. For these surfaces, the gluing identifies not the opposite sides of a polygon, but its alternating sides: 1– 3, 2–4, 5–7, 6–8, and so on. One could hope that if the polygon is still a regular 4g-gon, then this gluing would lead to a surface with the same diameter R. However, this is not true—the diameter of these surfaces appears to be greater than R in simulations. This observation is a reflection of the fact that the symmetries of a surface play a crucial role in defining its geometric properties including the diameter, so one should select very carefully a right set of symmetries of a surface in calculating its diameter. Our proof is an example of this strategy applied to a particular class of highly symmetric surfaces. Its generalization to other surfaces with other groups of symmetry presents an interesting open problem.

The next section contains the complete proofs of all the theorems and propositions above.

4 Proofs

Theorem 2

The diameter $\mathscr {D}_g$ of $S_g$ is at least R, $\mathscr {D}_g \ge R$.

Proof

Take ${[z]=[0]}$ and $[w]=[v]$. We will show that $\delta ^\star ([0],[v]) = R$, from which the theorem follows immediately. For this, we use that the fundamental polygon P is also the Dirichlet polygon of [0],

$$\begin{aligned} D_0 = \{ p \mid \delta (0,p) < \delta (f(0),p) \text { for all } f \in \mathscr {F}_g, ~ f \ne I \} . \end{aligned}$$

(18)

where I is the identity. To see this, first note that points p on the geodesic segment ${\overline{v_iv_{i+1}}}$ satisfy ${\delta (0,p) = \delta (t_i(0),p)}$ owing to the symmetry of the fundamental polygon. Next, denote by ${H_i}$ the half-plane bounded by this line and containing 0. Then

$$\begin{aligned} D_0&= \{ p \mid \delta (0,p)< \delta (f(0),p) \text { for all } f \in \mathscr {F}_g, ~ f \ne I \} \nonumber \\&\subseteq \{ \delta (0,p)< \delta (t_i(0),p), ~ 0 \le i< 4g \} = \bigcap _{0 \le i < 4g} H_i , \end{aligned}$$

(19)

and the last expression is just P, thus ${D_0 \subseteq P}$. Since Dirichlet polygons are fundamental polygons, which all have the same hyperbolic area [14, Thm. 9.1.3], we have ${\text {area} (D_0) = \text {area} (P)}$ and conclude ${D_0 = P}$.

Now, since the elements of [v] contained in P, which are just the $v_i$, are the closest v-images to 0 and lie a distance R from 0, we have $\delta ^\star ([0],[v]) = R$. Therefore ${\mathscr {D}_g \ge R}$. $\square$

Proposition 1

Let ${\phi }$ be any isometry of $\mathbb {D}$ that maps the fundamental polygon to any of its dual polygons. Then the projection ${\phi ^\star : S_g \rightarrow S_g}$ given by

$$\begin{aligned} \phi ^\star ([z]) = [\phi (z)] \end{aligned}$$

(20)

is well-defined and is an isometric automorphism of $S_g$. In particular, dual polygons are fundamental domains.

Proof

First we will show the rotational symmetry of the quotient surface. It suffices to show that ${\theta \mathscr {F}_g \theta ^{-1} = \mathscr {F}_g}$ by the argument given in Sect. 3, where ${\theta }$ is the counterclockwise rotation of ${\mathbb {D}}$ by ${\pi /2g}$. We will use the property of the generators of ${\mathscr {F}_g}$ that ${\theta t_i \theta ^{-1} = t_{i+1}}$ for all i, and the fact which follows from elementary group theory that ${\theta \mathscr {F}_g \theta ^{-1} = \mathscr {F}_g}$ if and only if ${\theta \mathscr {F}_g \theta ^{-1} \subseteq \mathscr {F}_g}$. We further note that it suffices to show ${\theta t_i \theta ^{-1} \subseteq \mathscr {F}_g}$ for all i, since this implies for all $f = t_{i_1} t_{i_2} \cdot \cdot \cdot t_{i_k} \in \mathscr {F}_g$ that

$$\begin{aligned} \theta f \theta ^{-1} = \theta t_{i_1} t_{i_2} \cdot \cdot \cdot t_{i_k} \theta ^{-1} =(\theta _{t_{i_1}}\theta ^{-1}) (\theta _{t_{i_2}}\theta ^{-1})\cdots (\theta _{t_{i_k}}\theta ^{-1}) \in \mathscr {F}_g . \end{aligned}$$

(21)

For an arbitrary generator ${t_i \in \mathscr {F}_g}$ we have

$$\begin{aligned} \theta t_i \theta ^{-1} = t_{i+1} \in \mathscr {F}_g , \end{aligned}$$

(22)

and therefore ${\theta \mathscr {F}_g \theta ^{-1} = \mathscr {F}_g}$. It follows that the isometry ${\theta ^\star }$, given by ${\theta ^\star ([p]) = [\theta (p)]}$ for points [p] on the quotient surface, is a well-defined isometry and therefore a symmetry of the quotient surface.

Next, we will show the same for ${\phi ^\star }$. Suppose that ${\phi }$ maps the fundamental polygon to the dual polygon D centered at the vertex v. Then for any generator ${t_i}$, the map ${t_i^\prime = \phi t_i \phi ^{-1}}$ maps D to one of its neighboring dual polygons centered at vertex ${v^\prime }$, such that ${t^\prime (v) = v^\prime }$ and ${t^\prime }$ fixes the geodesic line between v and ${v^\prime }$.

Now, choose ${h \in \mathscr {F}_g}$ that maps v to ${v^\prime }$. We will be done if we can show ${t^\prime = h}$, since this implies ${t^\prime \in \mathscr {F}_g}$ as desired. Since h is orientation-preserving, we can write it as a product of ${t^\prime }$ and an arbitrary rotation by ${\alpha }$ around ${v^\prime }$. Then ${h^{-1}}$ is the product of ${(t^\prime )^{-1}}$ and a rotation by ${- \alpha }$ around v. Pick one of the representatives of the fundamental polygon that has ${\overline{v v^\prime }}$ as an edge, such that the directed line segment ${\overline{v v^\prime }}$ is oriented counterclockwise along the polygon boundary. Then by the rotational symmetry of ${\mathscr {F}_g}$, every similar element of ${\mathscr {F}_g}$ that maps a vertex to its neighbor in the counterclockwise direction has the same form, a translation followed by a rotation by ${\alpha }$. Similarly, such maps in the clockwise direction are translations followed by rotations by ${- \alpha }$.

However, we could have chosen the other polygon that has edge ${\overline{v v^\prime }}$ in the clockwise orientation, and drawn the same conclusions above with the orientations reversed. So we are forced to conclude ${\alpha = - \alpha }$, thus either ${\alpha = 0}$ or ${\alpha = \pi }$. But h cannot have fixed points, and if ${\alpha = \pi }$ then h fixes the midpoint between v and ${v^\prime }$, hence ${\alpha = 0}$, so ${t^\prime = h}$. Therefore ${\phi \mathscr {F} \phi ^{-1} = \mathscr {F}}$, so ${\phi ^\star }$ is a symmetry of the quotient surface. $\square$

Proposition 2

To prove Theorem 1, it suffices to consider only the pairs of points z and w satisfying the following conditions:

• 1. z lies in triangle ${T = \Delta 0 v_1 v_2}$, Fig. 3,

• 2. $d_0(z) \ge d_v(w)$,

• 3. $d_v(w) \le s/2$.

Proof

For pairs z, w that do not meet at least one of the conditions above, our strategy will be to find another pair ${z^\prime ,w^\prime }$ that do meet the conditions, such that ${\delta (z,w) = \delta (z^\prime ,w^\prime )}$. Then the diameter of ${S_g}$, which is the maximum of ${\delta }$ over all z, w, is equal to the maximum of ${\delta }$ over just the z, w which satisfy the conditions above, so it will suffice to consider only those pairs.

Fig. 4

Division of the fundamental polygon into 8g isosceles triangles for ${g=2}$

Starting with an arbitrary pair z, w, let $\phi$ be any of the isometries from the fundamental polygon to a dual polygon, and $\phi ^\star$ the corresponding isometry of the quotient surface. Note that $\phi ^\star$ takes ${[0] \rightarrow [v]}$ and ${[v] \rightarrow [0]}$. Therefore ${d_0(\phi (p)) = d_v(p)}$ and ${d_v(\phi (p)) = d_0(p)}$ for points ${p \in \mathbb {D}}$. Now, for the given z, w consider the four quantities ${d_0(z), d_v(z), d_0(w), d_v(w)}$. We can divide the fundamental polygon into 8g congruent isosceles triangles (Fig. 4) each with one vertex at 0, one vertex at some ${v_i}$, and one vertex at the midpoint of an edge of the polygon, and side lengths R, s/2, s/2. Since z lies in one of these isosceles triangles, we have ${d_0(z) + d_v(z) \le s/2 + s/2 = s}$, and similarly for w. It follows that

$$\begin{aligned} M = \min \{ d_0(z), d_v(z), d_0(w), d_v(w) \} \le \frac{s}{2} . \end{aligned}$$

(23)

We now consider four cases, and in each case construct ${z^\prime ,w^\prime }$ for which conditions (2) and (3) are satisfied and ${\delta (z^\prime ,w^\prime ) = \delta (z,w)}$.

• 1. ${M = d_0(z)}$. Let ${z^\prime = \phi (w)}$ and ${w^\prime = \phi (z)}$. Then

  $$\begin{aligned} d_0 (z^\prime ) = d_v(w)&\ge d_0(z) = d_v(w^\prime ) \qquad \text {and} \end{aligned}$$

  (24)
  $$\begin{aligned} d_v(w^\prime ) = d_0(z)&\le \frac{s}{2} . \end{aligned}$$

  (25)

• 2. ${M = d_v(z)}$. Let ${z^\prime = w}$ and ${w^\prime = z}$. Then

  $$\begin{aligned} d_0 (z^\prime ) = d_0(w)&\ge d_v(z) = d_v(w^\prime ) \qquad \text {and} \end{aligned}$$

  (26)
  $$\begin{aligned} d_v(w^\prime ) = d_v(z)&\le \frac{s}{2} . \end{aligned}$$

  (27)

• 3. ${M = d_0(w)}$. Let ${z^\prime = \phi (z)}$ and ${w^\prime = \phi (w)}$. Then

  $$\begin{aligned} d_0 (z^\prime ) = d_v(z)&\ge d_0(w) = d_v(w^\prime ) \qquad \text {and} \end{aligned}$$

  (28)
  $$\begin{aligned} d_v(w^\prime ) = d_0(w)&\le \frac{s}{2} . \end{aligned}$$

  (29)

• 4. ${M = d_v(w)}$. Let ${z^\prime = z}$ and ${w^\prime = w}$. Then

  $$\begin{aligned} d_0 (z^\prime ) = d_0(z)&\ge d_v(w) = d_v(w^\prime ) \qquad \text {and} \end{aligned}$$

  (30)
  $$\begin{aligned} d_v(w^\prime ) = d_v(w)&\le \frac{s}{2} . \end{aligned}$$

  (31)

We have already demonstrated the rotational symmetry of ${S_g}$ in the proof of Prop. 1. Starting with $z^\prime ,w^\prime$ and rotating a sufficient number of times by $\pi /(2g)$, we can place ${z^\prime }$ in T. Furthermore, since rotations map vertices to vertices and fix 0, they preserve the quantities ${d_0(z^\prime ), d_v(z^\prime ), d_0(w^\prime ), d_v(w^\prime )}$, so the rotated ${z^\prime ,w^\prime }$ now satisfy all three conditions.$\square$

Theorem 3

Given w for which $d_v(w) \le s/2$, the function

$$\begin{aligned} f(z) = \min \left[ \delta (z,w_1), \delta (z,w_2) \right] \end{aligned}$$

attains its global maximum over the domain $\Omega _w$ on its boundary ${\partial \Omega _w}$.

Proof

Since f(z) is continuous and bounded on the compact region ${\Omega _w \cup \partial \Omega _w}$, f(z) attains a global maximum on this region.

Let M denote the midline of $w_1$ and $w_2$ (the locus of points equidistant from $w_1$ and $w_2$, also the perpendicular bisector of the geodesic segment $\overline{w_1w_2}$). Then M divides $\Omega _w$ into some set of open regions, $\{S_i\}$. We will first show that for any i and ${z_0 \in S_i}$, $z_0$ cannot be a global maximum of f(z).

Inside ${S_i}$ we have ${\delta (z, w_1) \ne \delta (z, w_2)}$, and therefore either ${\delta (z, w_1) < \delta (z, w_2)}$ or ${\delta (z, w_2) < \delta (z, w_1)}$. Assume without loss of generality that ${\delta (z, w_1) < \delta (z, w_2)}$. Then ${f(z_0) = \delta (z_0, w_1)}$ and ${f(z) = \delta (z, w_1)}$ in some open set around $z_0$. Therefore, we can always increase the value of f by moving $z_0$ in some suitable direction (away from $w_1$).

It remains to consider ${z_0 \in M \cap \Omega _w}$. The set ${M \cap \Omega _w}$ is a union of segments ${\{M_i\}}$ which lie in $\Omega _w$ and have endpoints on $\partial \Omega _w$. Take ${z_0 \in M_i}$. In this case we also have ${f(z_0) = \delta (z_0, w_1)}$. It suffices to show that $\delta (z, w_1)$ is maximized at one of the endpoints of $M_i$. However, this is a well-known result on the distance from points to line segments (see [21, Thm. 2.2]). Since these endpoints are on $\partial \Omega _w$, we have shown that the global maximum of f(z) is attained on $\partial \Omega _w$. $\square$

Theorem 4

Given w for which $d_v(w) \le s/2$, for all $z \in \partial \Omega _w$ we have

$$\begin{aligned} \min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R . \end{aligned}$$

Proof

We abbreviate ${a = d_0(z)}$, ${b = d_v(w)}$, ${R^{\prime } = \tanh (R/2)}$, and ${s^{\prime } = \tanh (s/4)}$.

Case I: We look at the radial segments of ${\partial \Omega _w}$ first, see Fig. 3, right. For z on ${\overline{0v_0}}$, consider the triangle with vertices z, ${v_0}$, and ${w_1}$ and side lengths b, ${\delta (z,w_1)}$, and ${R - a}$, respectively. By the triangle inequality,

$$\begin{aligned} b + (R - a) \ge \delta (z,w_1) \quad \Rightarrow \quad \delta (z,w_1) \le R - (a - b) \le R, \end{aligned}$$

(32)

and a similar argument for z on ${\overline{0v_2}}$ gives ${\delta (z,w_2) \le R}$, so that in either case ${\min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R}$.

Fig. 5

Illustration of z, ${w_1}$, and ${w_2}$, and angles ${\phi }$, ${\theta _1}$, ${\theta _2}$

Case II: Next we consider the circular arc of radius b centered at the origin (Fig. 3, right). For z on this arc we have ${a = b}$. Let ${\phi }$ denote the angle between ${\overline{0z}}$ and ${\overline{0v_1}}$, so that ${\phi \in [0, \pi /(2\,g)]}$. Let ${\theta _1}$ denote the angle between ${\overline{v_1w_1}}$ and ${\overline{v_1v_2}}$, and ${\theta _2}$ denote the angle between ${\overline{v_2w_2}}$ and the extension of ${\overline{v_1v_2}}$, Fig. 5.

We have the constraint ${\theta _1 = \theta _2}$, i.e. $w_1$ and $w_2$ make the same angle with the axis ${\overline{v_1v_0}}$, which is a consequence of Prop. 1. Now, we assume that ${\delta (z,w_1) > R}$ and ${\delta (z,w_2) > R}$ and seek a contradiction. Using the hyperbolic sine and cosine theorems to calculate the distances, we get after some algebra

$$\begin{aligned}&\delta (z,w_1)> R \Leftrightarrow \nonumber \\&\quad \left( 1 + R^{\prime ^2} \right) - 2 R^{\prime } \coth a \left[ \cos \left( \theta _1 + \frac{\pi }{4g} \right) + \cos \phi \right] \nonumber \\&\qquad + \cos \left( \theta _1 + \phi + \frac{\pi }{4g} \right) + R^{\prime ^2} \cos \left( \theta _1 - \phi + \frac{\pi }{4g} \right) > 0, \end{aligned}$$

(33)

and a similar equation arises from ${\delta (z,w_2) > R}$. Solving Eq. (33) yields

$$\begin{aligned} \frac{\cos \left( \frac{\theta _1 + \phi }{2} + \frac{\pi }{8g} \right) }{\sin \left( \frac{\theta _1 - \phi }{2} + \frac{\pi }{8g} \right) } \in \left( - \infty , R^{\prime } \tanh \left( \frac{a}{2} \right) \right) \cup \left( \frac{R^{\prime }}{\tanh \left( \frac{a}{2} \right) }, \infty \right) . \end{aligned}$$

(34)

Notice that ${R^{\prime } \tanh (a/2)}$ is an increasing function of a, while ${R^{\prime }/\tanh (a/2)}$ is a decreasing function of a, so it suffices to consider the case where a is maximal, ${a = s/2}$. Plugging this in gives

$$\begin{aligned} \frac{\cos \left( \frac{\theta _1 + \phi }{2} + \frac{\pi }{8g} \right) }{\sin \left( \frac{\theta _1 - \phi }{2} + \frac{\pi }{8g} \right) } \in \left( - \infty , R^{\prime } s^\prime \right) \cup \left( \frac{R^{\prime }}{s^\prime }, \infty \right) . \end{aligned}$$

(35)

Solving for ${\alpha = \theta _1 - \phi + \pi /(4g)}$ gives

$$\begin{aligned} \tan \left( \frac{\alpha }{2} \right) \in \left( \frac{\cos \phi - \frac{R^\prime }{s^\prime }}{\sin \phi }, \frac{\cos \phi - R^\prime s^\prime }{\sin \phi } \right) . \end{aligned}$$

(36)

A similar analysis of the second inequality, ${\delta (z,w_2) > R}$ using ${\theta _1 = \theta _2}$ gives

$$\begin{aligned}&\tan \left( \frac{\alpha }{2} \right) \in \left( - \infty , \frac{\sin \left( \frac{\pi }{2g} - \phi \right) }{\cos \left( \frac{\pi }{2g} - \phi \right) - \frac{R^{\prime }}{s^{\prime }}} \right) \nonumber \\&\quad \cup \left( \frac{\sin \left( \frac{\pi }{2g} - \phi \right) }{\cos \left( \frac{\pi }{2g} - \phi \right) - R^{\prime } s^{\prime }}, \infty \right) . \end{aligned}$$

(37)

However, since the inequalities

$$\begin{aligned} \frac{\cos \phi - \frac{R^\prime }{s^\prime }}{\sin \phi } \le \frac{\sin \left( \frac{\pi }{2g} - \phi \right) }{\cos \left( \frac{\pi }{2g} - \phi \right) - \frac{R^{\prime }}{s^{\prime }}} \end{aligned}$$

(38)

and

$$\begin{aligned} \frac{\cos \phi - R^\prime s^\prime }{\sin \phi } \ge \frac{\sin \left( \frac{\pi }{2g} - \phi \right) }{\cos \left( \frac{\pi }{2g} - \phi \right) - R^{\prime } s^{\prime }} \end{aligned}$$

(39)

have no solutions in ${\phi \in [ 0, \pi /(2g)]}$, the sets in Eqs. (36, 37) are disjoint, and we conclude that the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta (z,w_1)> R \\ \delta (z,w_2) > R \end{array}\right. } \end{aligned}$$

(40)

has no solutions, so ${\min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R}$.

Case III: Finally, we consider z on the edge ${\overline{v_1v_2}}$. Let ${x = \delta (z,v_1)}$ and ${\alpha = \angle v_2v_1w_1}$. Applying the first hyperbolic law of cosines to triangle ${\Delta z v_1 w_1}$ gives

$$\begin{aligned} \cosh \left( \delta (z, w_1) \right) = \cosh b \cosh x - \sinh b \sinh x \cos \alpha . \end{aligned}$$

(41)

Assuming for the sake of contradiction that ${\delta (z,w_1) > R}$ and ${\delta (z,w_2) > R}$, then from the first inequality we find

$$\begin{aligned} \cosh b \cosh x - \sinh b \sinh x \cos \alpha > \cosh R , \end{aligned}$$

(42)

which implies

$$\begin{aligned} \cos \alpha < \frac{\cosh b \cosh x - \cosh R}{\sinh b \sinh x} . \end{aligned}$$

(43)

Similarly, the second inequality ${\delta (z,w_2) > R}$ yields

$$\begin{aligned} \cos \alpha > \frac{\cosh R - \cosh b \cosh (s - x)}{\sinh b \sinh (s - x)} . \end{aligned}$$

(44)

However, for inequalities (43) and (44) to have solutions in ${\alpha }$, we must have

$$\begin{aligned} \frac{\cosh b \cosh x - \cosh R}{\sinh b \sinh x} > \frac{\cosh R - \cosh b \cosh (s - x)}{\sinh b \sinh (s - x)} . \end{aligned}$$

(45)

Simplifying yields

$$\begin{aligned} \cosh \left( \frac{s}{2} \right) \cosh \left( x - \frac{s}{2} \right) < \cosh b . \end{aligned}$$

(46)

Notice that the right hand side is an increasing function of b, thus it suffices to disprove the inequality in the case where b is maximal, $b = s/2$. Plugging this in and simplifying the resulting inequality gives

$$\begin{aligned} \cosh \left( x - \frac{s}{2} \right) < 1 , \end{aligned}$$

(47)

which has no solutions in x. Therefore our assumption was false, so ${\min \left[ \delta (z,w_1), \delta (z,w_2) \right] \le R}$. $\square$

Theorem 1

${\mathscr {D}_g = R}$.

Proof

We first show that for all [z], [w],

$$\begin{aligned} \delta ^\star ([z],[w]) \le R . \end{aligned}$$

(48)

By Prop. 2, it suffices to consider the case ${z \in \Delta 0v_1v_2}$, ${d_0(z) \ge d_v(w)}$, ${d_v(w) \le s/2}$. Then by Theorem 3, for all such w the function ${f(z) = \delta ^\star ([z],[w])}$ defined on the domain ${\Omega _w}$ attains a global maximum M on the boundary ${\partial \Omega _w}$, and by Theorem 4, $M \le R$. This proves Eq. (48), and therefore $\mathscr {D}_g \le R$. But Theorem 2 says that $\mathscr {D}_g \ge R$. We conclude that $\mathscr {D}_g = R$. $\square$