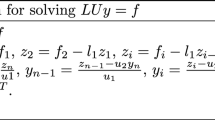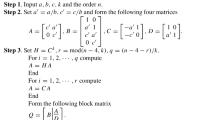Skip to main content
SpringerLink
Log in

A novel numerical algorithm for solving linear systems with periodic pentadiagonal Toeplitz coefficient matrices

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

In the present paper, we mainly consider the direct solution of periodic pentadiagonal Toeplitz linear systems. By exploiting the low-rank and Toeplitz structure of the coefficient matrix, we derive a new matrix decomposition of periodic pentadiagonal Toeplitz matrices. Based on this matrix decomposition form and combined with the Sherman-Morrison-Woodbury formula, we propose an efficient algorithm for numerically solving periodic pentadiagonal Toeplitz linear systems. Furthermore, we present a fast and reliable algorithm for evaluating the determinants of periodic pentadiagonal Toeplitz matrices by a certain type of matrix reordering and partitioning, and linear transformation. Numerical examples are given to demonstrate the performance and effectiveness of our algorithms. All of the experiments are performed on a computer with the aid of programs written in Matlab.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  • Amar AJ, Blackwell BF, Edwards JR (2008) One-dimensional ablation using a full newton’s method and finite control volume procedure. J Thermophys Heat Transfer 22(1):71–82

    Article  Google Scholar 

  • Batista M, Ibrahim Karawia ARA (2009) The use of the Sherman-Morrison-Woodbury formula to solve cyclic block tri-diagonal and cyclic block penta-diagonal linear systems of equations. Appl Math Comput 210(2):558–563

    MathSciNet  Google Scholar 

  • Buzbee BL, Golub GH, Nielson CW (1970) On direct methods for solving poissons equations. SIAM J Numer Anal 7(4):627–656

    Article  MathSciNet  Google Scholar 

  • Chen M (1987) On the solution of circulant linear systems. SIAM J Numer Anal 24(3):668–683

    Article  MathSciNet  Google Scholar 

  • Davis TA (2006) Direct Methods for Sparse Linear Systems. SIAM

  • Demmel JW (1997) Applied Numerical Linear Algebra. SIAM

  • Du L, Sogabe T, Zhang SL (2018) A fast algorithm for solving tridiagonal quasi-Toeplitz linear systems. Appl Math Lett 75:74–81

    Article  MathSciNet  Google Scholar 

  • El-Mikkawy MEA (2005) A new computational algorithm for solving periodic tri-diagonal linear systems. Appl Math Comput 161(2):691–696

    MathSciNet  Google Scholar 

  • Gou T, Sandu A (2011) Continuous versus discrete advection adjoints in chemical data assimilation with cmaq. Atmos Environ 45(28):4868–4881

    Article  Google Scholar 

  • Householder A (1964) The Theory of Matrices in Numerical Analysis. Dover, Blaisdell, Waltham

    Google Scholar 

  • Jia J, Jiang Y (2013) A structure preserving matrix factorization for solving general periodic pentadiagonal Toeplitz linear systems. Comput Math Appl 66(6):965–974

    Article  MathSciNet  Google Scholar 

  • Jia J, Li S (2017) An efficient numerical algorithm for the determinant of a cyclic pentadiagonal Toeplitz matrix. Comput Math Appl 74(12):2992–2999

    Article  MathSciNet  Google Scholar 

  • Jia J, Wang F (2023) On the efficient and accurate determinant evaluation of periodic tridiagonal Toeplitz matrices. J Math Chem 61(7):1504–1521

    Article  MathSciNet  Google Scholar 

  • Jiang Z, Zhou Y, Jiang X, Zheng Y (2023) Analytical potential formulae and fast algorithm for a horn torus resistor network. Phys Rev E 107:044123

    Article  MathSciNet  Google Scholar 

  • Jiang X, Zhang G, Zheng Y, Jiang Z (2024) Explicit potential function and fast algorithm for computing potentials in \(\alpha \times \beta \) conic surface resistor network. Expert Syst Appl 238:122157

    Article  Google Scholar 

  • Karawia AA (2006) A computational algorithm for solving periodic penta-diagonal linear systems. Appl Math Comput 174(1):613–618

    MathSciNet  Google Scholar 

  • Khan A, Khan I, Aziz T (2006) Sextic spline solution of a singularly perturbed boundary-value problems. Appl Math Comput 181(1):432–439

    MathSciNet  Google Scholar 

  • Kong Q, Jia J (2015) A structure-preserving algorithm for linear systems with circulant pentadiagonal coefficient matrices. J Math Chem 53(7):1617–1633

    Article  MathSciNet  Google Scholar 

  • Liu Y, Jiang Z, Jiang X (2020) Two types of interesting fibonacci-min matrices. Adv Appl Discrete Math 24:13–25

    Google Scholar 

  • Martin A, Trepanier JY, Reggio M, Xueyan G (2007) Transient ablation regime in circuit breakers. Plasma Sci Technol 9(6):653

    Article  Google Scholar 

  • Meng Q, Jiang X, Jiang Z (2021) Interesting determinants and inverses of skew Loeplitz and Foeplitz matrices. J Appl Anal Comput 11(6):2947–2958

    MathSciNet  Google Scholar 

  • Meng Q, Zheng Y, Jiang Z (2022) Determinants and inverses of weighted Loeplitz and weighted Foeplitz matrices and their applications in data encryption. J Appl Math Comput 68(6):3999–4015

    Article  MathSciNet  Google Scholar 

  • Meng Q, Zheng Y, Jiang Z (2022) Exact determinants and inverses of (2,3,3)-Loeplitz and (2,3,3)-Foeplitz matrices. Comput Math Appl 41(1):35

    Article  MathSciNet  Google Scholar 

  • Mikkawy ME, Rahmo ED (2009) A new recursive algorithm for inverting general periodic pentadiagonal and anti-pentadiagonal matrices. Appl Math Comput 207(1):164–170

    MathSciNet  Google Scholar 

  • Navon IM (1987) Pent: A periodic pentadiagonal systems solver. Commun Appl Numer Methods 3(1):63–69

    Article  Google Scholar 

  • Nemani S, Garey LE (2002) An efficient method for second order boundary value problems with two point boundary conditions. Int J Comput Math 79(9):1001–1008

    Article  MathSciNet  Google Scholar 

  • Paprzycki M, Gladwell I (1993) A parallel chopping algorithm for ode boundary value problems. Parallel Comput 19(6):651–666

    Article  Google Scholar 

  • Patil PG, Swamy Y (2008) An efficient model for vibration control by piezoelectric smart structure using finite element method. Int J Comput Sci Netw Secur 8(11):258–264

    Google Scholar 

  • Rosen KH (2007) Discrete Mathematics and Its Applications. The McGraw Hill Companies, New York

    Google Scholar 

  • Sachs EW, Strauss AK (2008) Efficient solution of a partial integro-differential equation in finance. Appl Numer Math 58(11):1687–1703

    Article  MathSciNet  Google Scholar 

  • Sogabe T (2008) New algorithms for solving periodic tridiagonal and periodic pentadiagonal linear systems. Appl Math Comput 202(2):850–856

    MathSciNet  Google Scholar 

  • Wang S, Jiang Z, Zheng Y (2020) Determinants, inverses and eigenvalues of two symmetric positive definite matrices with pell and pell-lucas numbers. Adv Diff Eq Control Processes 22(83–95):28

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous referees for their valuable comments and suggestions that substantially enhanced the quality of the manuscript.

Funding

Not applicable.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xidian University, Xi’an, Shaanxi, 710071, China

    Ji-Teng Jia & Yi-Fan Wang

Authors
  1. Ji-Teng Jia
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Fan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Ji-Teng Jia: Conceived, designed and performed the analysis, and wrote the manuscript.

Yi-Fan Wang: Performed the numerical experiments and prepared the manuscript.

Corresponding author

Correspondence to Ji-Teng Jia.

Ethics declarations

Conflict of interest

The authors declare that they have no Conflict of interest.

Ethical Approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jia, JT., Wang, YF. A novel numerical algorithm for solving linear systems with periodic pentadiagonal Toeplitz coefficient matrices. Comp. Appl. Math. 43, 232 (2024). https://doi.org/10.1007/s40314-024-02754-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-024-02754-y

Keywords

Mathematics Subject Classification

Search

Navigation