1 Introduction

Approximation and interpolation methods are powerful tools that are currently used in several real applications. Some examples are the design of curves and surfaces, geolocation, image processing, applications in medicine, and many others. Specifically, interpolants based on splines or approximants constructed using B-splines have been used for image compression (see, e.g. Unser 1999; Forster 2011), computer-aided geometric design (see, e.g. Boehm 1986; Sarfraz 1998), generation of curves (see e.g. Zheng et al. 2005) or real applications such as ship hull design (see e.g. Rogers and Satterfield 1980; Nowacki 2010; Katsoulis et al. 2019) or medical image processing (see, e.g. Lehmann et al. 2001).

The term quasi-interpolation is used to denote the construction of accurate approximations of a particular set of data obtained from a given function. As mentioned in Lyche et al. (2018), a quasi-interpolant to f provides a “reasonable” approximation to f. For example, interpolation and least squares are considered quasi-interpolation techniques. It is always desirable that the computational cost to obtain these approximations is low. Usually, quasi-interpolation techniques are obtained through the linear combination of blending functions with compact support. These blending functions are usually selected so that they are a convex partition of unity. It is also considered advantageous that the coefficients of the linear combination only involve a local stencil of the original data, in order to maintain the locality of the approximation obtained. The objective is to attain local control of the approximation and also to assure numerical stability. Quasi-interpolants constructed using polynomial spline spaces are widely known and used and are considered a powerful tool for the approximation of data that can be extended easily to several dimensions using tensor product (de Boor 1990; de Boor and Fix 1973; Speleers 2017; Lyche and Schumaker 1975; Sablonnière 2005). The main characteristic of the methods based on B-splines is the smoothness of the resultant function when the data do not present any strong gradient or discontinuity. However, they produce non-desirable effects around the singularities. Recently, some papers have dealt with this problem (see Amat et al. 2023; Aràndiga et al. 2023).

In particular, we consider a uniform sampling of the function \(f \in C^{p+1}({\mathbb {R}})\) and denote the nodes of the mesh by \(x_n = nh, n \in {\mathbb {Z}}\). The values of the function over the mesh are \(\{f_n=f (nh)\}\). With this information, we can compute approximations of f with \(O(h^{p+1})\) order of accuracy using local combinations of B-spline bases \(B_p\) of degree p (Lyche et al. 2018; Speleers 2017), with equidistant nodes \(S_p = \left\{ -\frac{p+1}{2},\ldots ,\frac{p+1}{2}\right\} \) and support \(I_p =\left[ -\frac{p+1}{2},\frac{p+1}{2}\right] \), by means of the operator

$$\begin{aligned} Q_p(f)(x)=\sum _{n\in {\mathbb {Z}}}L_{p}\left( f_{n,p}\right) B_{p}\left( \frac{x}{h}-n\right) , \end{aligned}$$
(1)

where the linear operator \(L_p:{\mathbb {R}}^{2\left\lfloor \frac{p}{2} \right\rfloor +1}\rightarrow {\mathbb {R}}\) is defined following Speleers (2017) as

$$\begin{aligned} L_p(f_{n,p})=\sum _{j=-\left\lfloor \frac{p}{2} \right\rfloor }^{\left\lfloor \frac{p}{2} \right\rfloor } c^p_{j} f_{n+j}, \end{aligned}$$
(2)

where \(c^p_{j}\), \(j=-\left\lfloor \frac{p}{2} \right\rfloor ,\ldots ,\left\lfloor \frac{p}{2} \right\rfloor \) can be written as

$$\begin{aligned} c^p_{j}=\sum _{l=0}^{\Bigg \lceil \frac{p+1}{2} \Bigg \rceil -1}\frac{t(2l+p+1,p+1)}{{{2l+p+1}\atopwithdelims (){p+1}}}\sum _{i=0}^{2l}\frac{(-1)^i}{i!(2l-i)!}\delta _{l-i+\Bigg \lceil \frac{p+1}{2}\Bigg \rceil , j+1+\left\lfloor \frac{p}{2}\right\rfloor }, \end{aligned}$$
(3)

with \(\delta _{i,j}\) being the Kronecker delta function:

$$\begin{aligned} \delta _{i,j}=\left\{ \begin{array}{ll} 1, &{}\hbox {if} \,\, i=j, \\ 0, &{}\hbox {if} \,\, i\ne j. \\ \end{array} \right. \end{aligned}$$

The t(i, j) are the central factorial numbers of the first kind (Speleers 2017; Butzer et al. 1989). A recursive computation of these numbers can be done using the following expressions:

$$\begin{aligned} t(i,j)=\left\{ \begin{array}{ll} 0, &{} \hbox {if}\,\, j>i, \\ 1, &{} \hbox {if}\,\, j=i, \\ t(i-2,j-2)-\left( \frac{i-2}{2}\right) ^2t(i-2,j), &{} \hbox {if} \,\, 2\le j <i, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} t(i,0)=0,\quad t(i,1)=\prod _{l=1}^{i-1}\left( \frac{i}{2}-l\right) ,\,\, i\ge 2, \end{aligned}$$

where \(t(0,0)=t(1,1)=1, t(0,1)=t(1,0)=0\).

In this work, we will centre our attention in cases \(p=2,3\), although the same technique can be used for greater p. Thus, we particularise the quasi-interpolation operator \(Q_p\) with the form of (1) for \(p=2,3\):

$$\begin{aligned} Q_p(f)(x)=\sum _{n\in {\mathbb {Z}}}L_p\left( f_{n,3}\right) B_p\left( \frac{x}{h}-n\right) , \quad n\in {\mathbb {Z}}, \end{aligned}$$
(4)

where

$$\begin{aligned}{} & {} L_p\left( f_{n-1},f_n,f_{n+1}\right) =\sum _{j=-1}^1c_j^pf_{n+j},\quad \nonumber \\{} & {} \qquad \text {with} \,\, c^2_{-1}=c^2_{1}=-\frac{1}{8},\,\,c^2_{0}=\frac{5}{4};\,\, c^3_{-1}=c^3_{1}=-\frac{1}{6},\,\,c^3_{0}=\frac{4}{3}. \end{aligned}$$
(5)

It is known that this quasi-interpolation operator reproduces the space of polynomials of degree less or equal than p on finite intervals I, Lyche et al. (2018), such that

$$\begin{aligned} ||f - Q_p(f)||_{\infty ,I}=O(h^{p+1}), \end{aligned}$$
(6)

as \(h \rightarrow 0\). It is also known that, close to jump discontinuities, the operator losses the accuracy due to the presence of oscillations, and close to kinks (discontinuities in the first derivative), due to the smearing of the singularity.

The aim of this work is to design correction terms for the linear operator \(Q_p\), in order to reconstruct with full accuracy piecewise smooth functions that present singularities at one or more points. With this objective in mind, we will take inspiration from the immersed interface method (IIM) (see, e.g. Leveque and Li 1994; Li and Ito 2006), which was originally proposed for the solution of elliptic partial differential equations with discontinuities. Correction terms for quadratic and cubic splines will be presented in Sects. 2 and 3, where we also analyse some properties of the construction. Section 5 is dedicated to present some numerical experiments that support the theoretical results obtained.

2 Correction of the quadratic B-spline quasi-interpolant

Fig. 1
figure 1

An example of a quadratic B-spline base and the division of the domain in two subdomains, which depend on the location of the singularity \(x^*\)

Full size image

We start by assuming that the position \(x^*\in [x_{n-\frac{1}{2}}, x_{n+\frac{1}{2}}]\) of an isolated singularity is known or can be approximated with enough accuracy. It is known that, for data given in the point values, i.e. samplings of a function f over an interval, the location of a jump discontinuity in the function is lost during the discretization process, but kinks (discontinuities in the first-order derivative) can still be located. For data given in the cell-average setting, i.e. the data are obtained from the integration of a function in certain intervals, jumps in the function and in the first-order derivative can be located. In this article, we will centre our attention on the point value setting, as the extension to the cell-average setting is straightforward considering the primitive function (Aràndiga and Donat 2000).

The obtention of correction terms can be done expanding in a smart way some of the values of \(f_n\) contained in the operator \(L_p\) using Taylor expansions. Of course, after finishing this process, we need to assure that the B-splines that compose the base, do not cross the singularity at \(x^*\). This means that we need to divide the domain in subdomains limited by the location of the singularity or singularities. An example of a quadratic B-spline base and the division of the domain in two subdomains can be seen in Fig. 1. We have represented the subdomain to the left of \(x^*\) in red, and the subdomain to the right in blue. In this figure we have also presented the operator \(L_p(f_{n, 3})\) for \(p=2\). We can see how modifying the values of this operator, which cross the singularity, is not enough to attain full accuracy, as the B-spline (that is multiplied by this operator) might still cross the singularity.

Let us now explain how to proceed to obtain the correction terms that we propose. Let l be a natural number, \(f^-\in {\mathcal {C}}^l([a, x^*]), f^+\in {\mathcal {C}}^l([x^*,b])\), where we have used the superindex − to express the function values at the left of the singularity, and the \(+\) superindex to express the function values to the right of the singularity, with

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} f^-(x),&{} x\le x^*,\\ f^+(x),&{} x>x^*, \end{array}\right. } \end{aligned}$$
(7)

and writing the jumps in the derivatives of f as

$$\begin{aligned} \left[ f^{(l)}\right] = f_{\underbrace{x\cdots x}_l}^{+}(x^{*}) - f_{\underbrace{x\cdots x}_l}^{-}(x^{*}), \end{aligned}$$
(8)

where we have denoted the lth derivative of \(f^\pm \) at \(x^*\) by \(f^{\pm }_{\underbrace{x\cdots x}_l}(x^{*})\). Let us discuss later about how to approximate these jumps, and which accuracy is needed.

Looking at Fig. 2 and at the expression of the operator \(L_p\) in (5), it should be clear that the approximation error of the spline in the interval \([x_{n-\frac{1}{2}}, x_{n+\frac{1}{2}}]\) that contains the singularity, is due to the fact that the operator \(L_2(f_{n,3})\) and \(L_2(f_{n+1,3})\) are crossing the discontinuity. Moreover, it is also due to the fact that the B-spline bases are also crossing the discontinuity. Thus, now it should be clear that, not only it is necessary to correct the operator, but also to divide the domain so that information from only one side of the discontinuity is used in the computation. In order to compute the amount of error that each B-spline function contributes to the total error of the approximation in the interval \([x_{n-\frac{1}{2}}, x_{n+\frac{1}{2}}]\), we can just use Taylor expansions on the expression of the \(L_p\) operator. For example, we can see in Fig. 2 that \(L_2(f_{n,3})\) crosses the singularity, so we can use the Taylor expansions of the value \(f_{j}\) around \(x^*\), and then use the jump relations \([f], [f'], [f'']\) in (8) to express the values to the left of the singularity in terms of the values to its right (or viceversa).

If we assume that we know the jumps in (8), or accurate enough approximations, using Taylor expansions, we can write

$$\begin{aligned} \begin{aligned} f^-(x_n)&=f^-_n=f^-(x^*)-f^-_x(x^*) \alpha +\frac{1}{2}f^-_{xx}(x^*) \alpha ^2-\frac{1}{3!}f^-_{xxx}(x^*) \alpha ^3+O(h^4),\\ f^+(x_n)&=f^+_n=f^+(x^*)-f^+_x(x^*) \alpha +\frac{1}{2}f^+_{xx}(x^*) \alpha ^2-\frac{1}{3!}f^+_{xxx}(x^*) \alpha ^3+O(h^4),\\ f^-(x_{n+1})&=f^-_{n+1}=f^-(x^*)+f^-_x(x^*) \beta +\frac{1}{2}f^-_{xx}(x^*) \beta ^2+\frac{1}{3!}f^-_{xxx}(x^*) \beta ^3+O(h^4),\\ f^+(x_{n+1})&=f^+_{n+1}=f^+(x^*)+f^+_x(x^*) \beta +\frac{1}{2}f^+_{xx}(x^*) \beta ^2+\frac{1}{3!}f^+_{xxx}(x^*) \beta ^3+O(h^4), \end{aligned} \end{aligned}$$
(9)

where \(\alpha =x^*-x_n\) and \(\beta =x_{n+1}-x^*\). Subtracting, we obtain

$$\begin{aligned} \begin{aligned} f_n^+&=f_n^-+[f]-[f']\alpha +\frac{1}{2}[f''] \alpha ^2-\frac{1}{3!}[f'''] \alpha ^3+O(h^4),\\ f_{n+1}^+&=f_{n+1}^-+[f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3+O(h^4). \end{aligned} \end{aligned}$$
(10)

Using the same process, similar expressions can be obtained for the values \(f_{n-2}, f_{n-1}\), and \(f_{n+2}\), which are involved in the computation of the approximation in the interval \([x_{n-\frac{1}{2}}, x_{n+\frac{1}{2}}]\), as presented in Fig. 1.

For the quadratic spline, in order to analyse the local truncation error introduced by each B-spline, it is much simpler to consider one of the elements \(L_p\left( f_{n,3}\right) \cdot B_p\left( \frac{\cdot }{h}-n\right) \) of the quasi-interpolant in (4) and to determine in which part of the support of the B-spline the discontinuity falls. Considering the B-spline \(B_2\left( \frac{\cdot }{h}-n\right) \) represented in Fig. 1 (the central one), we are ready to state the following Lemma, which will provide the accuracy attained by the quadratic quasi-interpolant when the data are affected by a discontinuity.

Lemma 1

Let consider the following partition:

$$\begin{aligned} {[}x_{n-\frac{3}{2}},x_{n+\frac{3}{2}}]{} & {} =[x_{n-\frac{3}{2}},x_{n-1})\cup [x_{n-1},x_{n})\cup [x_{n},x_{n+1})\cup [x_{n+1},x_{n+\frac{3}{2}}]\\{} & {} =:I_n^{-1}\cup I_n^0\cup I_n^1 \cup I_n^2, \end{aligned}$$

and a singularity \(x^*\in I_n^j, \,\, \, j=-1,0,1,2\) then

$$\begin{aligned} \begin{aligned} L_2(f_{n,3})-L_2(f^\pm _{n,3})=C_{j}^\pm (f_{n,3})+O(h^3). \end{aligned} \end{aligned}$$
(11)

being for \(j=-1\)

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{-1}^-(f_{n,3})=[f] + [f'] (\beta + h) + [f''] \left( \frac{1}{2} \beta ^2 + \beta h + \frac{3}{8} h^2\right) , &{} \text { if } x<x^*,\\ C_{-1}^+(f_{n,3})=0, &{} \text { if } x>x^*,\\ \end{array}\right. } \end{aligned}$$
(12)

for \(j=0\)

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{0}^-(f_{n,3})=\frac{9}{8}[f]+\frac{1}{8}[f'](9\beta -h)+\frac{1}{8}[f''](5 \beta ^2-\frac{1}{2}(\beta +h)^2, &{} \text { if } x<x^*,\\ C_{0}^+(f_{n,3})=\frac{1}{8} [f] - \frac{1}{8} [f'] \alpha + \frac{1}{16} [f''] \alpha ^2, &{} \text { if } x>x^*,\\ \end{array}\right. } \end{aligned}$$
(13)

for \(j=1\)

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{1}^-(f_{n,3})=-\frac{1}{8} [f] - \frac{1}{8} [f'] \beta - \frac{1}{16} [f''] \beta ^2, &{} \text { if } x<x^*,\\ C_{1}^+(f_{n,3})=-\frac{9}{8}[f]+\frac{1}{8}[f'](9\alpha -h)-\frac{1}{8}[f''](5 \alpha ^2-\frac{1}{2}(\alpha +h)^2, &{} \text { if } x>x^*,\\ \end{array}\right. } \end{aligned}$$
(14)

and for \(j=2\)

$$\begin{aligned} {\left\{ \begin{array}{ll} C_{2}^-(f_{n,3})=0, &{} \text { if } x<x^*,\\ C_{2}^+(f_{n,3})=-[f] + [f'] (\alpha + h) - [f''] \left( \frac{1}{2} \alpha ^2 + \alpha h + \frac{3}{8} h^2\right) , &{} \text { if } x>x^*,\\ \end{array}\right. } \end{aligned}$$
(15)

with \(\beta =x_{n+1}-x^*\) and \(\alpha =x^*-x_{n+1}\).

Proof

We have to consider the five cases presented in the Lemma. Let us start by the first one:

  • If \(x^*\in I^{-1}_n\), then the approximation is \(O(h^3)\) for \(x>x^*\), as all the values in the stencil of the operator \(L_2(f_{n,3})=-\frac{1}{8} f^+_{n-1} + \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\) belong to the \(+\) side of the domain, so \(C_{-1}^+(f_{n,3})=0\). For \(x<x^*\), we have that

    $$\begin{aligned} \begin{aligned} f_{n-1}^+&=f_{n-1}^-+[f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+O(h^3),\\ f_{n}^+&=f_{n}^-+[f]+[f'](\beta +h)+\frac{1}{2}[f''] (\beta +h)^2+O(h^3),\\ f_{n+1}^+&=f_{n+1}^-+[f]+[f'](\beta +2h)+\frac{1}{2}[f''] (\beta +2h)^2+O(h^3), \end{aligned} \end{aligned}$$
    (16)

    thus

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})=&\,-\frac{1}{8} f^+_{n-1} + \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}+\Bigg ([f] + [f'] (\beta + h) \\&+ [f''] \left( \frac{1}{2} \beta ^2 + \beta h + \frac{3}{8} h^2\right) \Bigg )+O(h^3)\\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}+C_{-1}^-(f_{n,3})+O(h^3). \end{aligned} \end{aligned}$$
    (17)

  • If \(x^*\in I^0_n\), then

    $$\begin{aligned} L_2(f_{n,3})=-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}. \end{aligned}$$

    Therefore, we have two cases. If \(x<x^*\), proceeding as before and replacing the \(+\) values in terms of the − ones, we obtain

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})=&\,-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}\\&+\left( \frac{9}{8}[f]+\frac{1}{8}[f'](9\beta -h)+\frac{1}{8}[f'']\left( 5 \beta ^2-\frac{1}{2}(\beta +h)^2\right) +O(h^3)\right) \\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}+C_0^-(f_{n,3})+O(h^3), \end{aligned} \end{aligned}$$
    (18)

    with \(\beta =x_{n}-x^*\).

    If \(x>x^*\), then we have to replace the − values in terms of the \(+\) ones. We obtain

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})=&\,-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}+\left( \frac{1}{8} [f] - \frac{1}{8} [f'] \alpha + \frac{1}{16} [f''] \alpha ^2\right) +O(h^3)\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}+C_0^+(f_{n,3})+O(h^3), \end{aligned}\nonumber \\ \end{aligned}$$
    (19)

    with \(\alpha =x^*-x_{n-1}\).

  • This case is symmetric to the previous one. If \(x^*\in I^1_n\), then

    $$\begin{aligned} L_2(f_{n,3})=-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^-_{n} - \frac{1}{8} f^+_{n+1}. \end{aligned}$$

    Therefore, we have two cases again. If \(x<x^*\),

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})&-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^-_{n} - \frac{1}{8} f^+_{n+1}\\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}-\left( \frac{1}{8} [f] + \frac{1}{8} [f'] \beta + \frac{1}{16} [f''] \beta ^2\right) +O(h^3)\\ =&\, -\frac{1}{8} f^-_{n-1}+ \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}+C_1^-(f_{n,3})+O(h^3), \end{aligned}\nonumber \\ \end{aligned}$$
    (20)

    with \(\beta =x_{n+1}-x^*\).

    If \(x>x^*\), then we have to replace the − values in terms of the \(+\) ones as before. We obtain

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})=&\,-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^-_{n} - \frac{1}{8} f^+_{n+1}\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\\&+\left( -\frac{9}{8}[f]+\frac{1}{8}[f'](9\alpha -h)-\frac{1}{8}[f''](5 \alpha ^2-\frac{1}{2}(\alpha +h)^2\right) +O(h^3)\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}+C_1^-(f_{n,3})+O(h^3), \end{aligned} \end{aligned}$$
    (21)

    with \(\alpha =x^*-x_{n-1}\).

  • The next case is symmetric to the first one. If \(x^*\in I^2_n\), then the approximation is \(O(h^3)\) for \(x<x^*\). Remind that, in this case, all the values in the stencil of the operator \(L_2(f_{n,3})=-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}\) belong to the − side of the domain, so \(C^-(f_{n,3})=0\). For \(x>x^*\), we have that

    $$\begin{aligned} \begin{aligned} L_2(f_{n,3})=&\,-\frac{1}{8} f^-_{n-1} + \frac{5}{4} f^-_{n} - \frac{1}{8} f^-_{n+1}\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}\\&+\Bigg (-[f] + [f'] (\alpha + h) - [f''] \left( \frac{1}{2} \alpha ^2 + \alpha h + \frac{3}{8} h^2\right) \Bigg )+O(h^3)\\ =&\, -\frac{1}{8} f^+_{n-1}+ \frac{5}{4} f^+_{n} - \frac{1}{8} f^+_{n+1}+C_2^+(f_{n,3})+O(h^3), \end{aligned} \end{aligned}$$
    (22)

    with \(\alpha =x^*-x_{n+1}\).

\(\square \)

After that, we define the values

$$\begin{aligned} C^\pm (f_{n+j,3})=C_j^\pm (f_{n,3}),\quad j=-1,0,1,2. \end{aligned}$$

With this lemma, and these definitions, we design the following non-linear operator:

$$\begin{aligned} {\widetilde{L}}_2(f_{n+j,3})(x)=L_2(f_{n+j,3})+C^2_{n+j}(x) \end{aligned}$$
(23)

being

$$\begin{aligned} C^2_{n+j}(x)={\left\{ \begin{array}{ll} -C^{-}(f_{n+j,3}), &{} x^*\in [x_n,x_{n+1}], \quad x<x^*, \\ -C^{+}(f_{n+j,3}), &{} x^*\in [x_n,x_{n+1}], \quad x>x^*, \\ 0, &{} \text {in other case}, \end{array}\right. } \end{aligned}$$
(24)

with \(j=-1,0,1,2,\) and its associate operator:

$$\begin{aligned} {\mathcal {Q}}_2(f)(x)=\sum _{n\in {\mathbb {Z}}}{\widetilde{L}}_2(f_{n,3})(x)B_2\left( \frac{x}{h}-n\right) . \end{aligned}$$
(25)

The approximation obtained using this new operator is of order of accuracy \(O(h^3)\). We give a proof in the following theorem.

Theorem 1

Let us consider \(j_0\in {\mathbb {Z}}\) and a finite interval I with \([x_{j_0-\frac{3}{2}}, x_{j_0+\frac{3}{2}}]\subset I\). If there exists a singularity placed at \(x^*\) in the interval \([x_{j_0-\frac{3}{2}}, x_{j_0+\frac{3}{2}}]\), then

$$\begin{aligned} ||{\mathcal {Q}}_2(f)-f||_{\infty ,I}=O(h^3). \end{aligned}$$

Proof

The proof is straightforward if we have a look to the expressions of the local truncation error in (17), (18), (19), (20), (21), and (22). \(\square \)

Corollary 1

If the jump relations in (8) are to be approximated, the accuracy needed is \(O(h^3)\) for [f], \(O(h^2)\) for \([f']\), and so on.

Proof

Having a look to the expressions of the error in (12), (13), (14) and (15), the proof is straightforward taking into account the contribution to the error of the approximation of [f], \([f']\), and so on. \(\square \)

Corollary 2

If the location of the discontinuity is to be approximated, the accuracy needed is \(O(h^3)\).

Proof

Having a look to the expressions of the error in (12), (13), (14) and (15), the proof is straightforward taking into account the contribution to the error of the approximation of \(\beta \). \(\square \)

Corollary 3

The error of the corrected spline is smooth and retains the smoothness of the B-splines bases.

Proof

From the expressions of the error in (12), (13), (14) and (15), it is clear that the error of the spline before or after the correction retains the smoothness of the B-splines bases. \(\square \)

3 Correction of the cubic B-spline quasi-interpolant

Fig. 2
figure 2

An example of a cubic B-spline base and the division of the domain in two subdomains. In this figure, \(x^*\) represents the location of the singularity

Full size image

The local truncation error for cubic splines can be obtained in a way similar to the one followed for quadratic splines. In Fig. 2, we have represented a base of cubic B-splines and the division of the domain in two subdomains as we did in Fig. 1.

As in the previous section, we can state the following Lemma, which provides the accuracy attained by the cubic quasi-interpolant. For the proof, we can proceed in the same way as before (moving the discontinuity to different positions and considering only one B-spline), or consider the four B-splines of the base and a discontinuity placed at a fix position. In this case, we have chosen the second option, as we found it clearer.

Lemma 2

Let us consider a singularity placed at \(x^*\) in the interval \([x_{n}, x_{n+1}]\), then

$$\begin{aligned} L_3(f_{n+j,3})-L^\pm _3(f_{n+j,3})=D^\pm (f_{n+j,3})+O(h^4), \quad j=-1,0,1,2 \end{aligned}$$

being for \(j=-1\)

$$\begin{aligned} \begin{aligned} D^+(f_{n-1,3}) =&\,-[f] + [f'] (\alpha + h) - \frac{1}{6} [f''] (3 \alpha ^2 + 6 \alpha h + 2 h^2)\\&+\frac{1}{6} [f''']\alpha (\alpha ^2 + 3 \alpha h + 2 h^2), \, \text { if } x<x^*,\\ D^-(f_{n-1,3}) =&0, \quad \text { if } x>x^*, \end{aligned} \end{aligned}$$
(26)

for \(j=0\)

$$\begin{aligned} \begin{aligned} D^-(f_{n,3})=&\,-\frac{1}{6}\left( [f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3\right) , \quad \text { if } x<x^*\\ D^+(f_{n,3})=&\,-\frac{7}{6} [f] + \frac{1}{6} [f'] ( 7\alpha - h) - \frac{1}{6} [f''] \left( 4 \alpha ^2 - \frac{1}{2} (\alpha + h)^2\right) \\&+ \frac{1}{6} [f'''] \left( \frac{4}{3} \alpha ^3 - \frac{1}{6} (\alpha + h)^3\right) , \quad \text { if } x>x^*, \end{aligned} \end{aligned}$$
(27)

for \(j=1\)

$$\begin{aligned} \begin{aligned} D^-(f_{n+1,3})=&\,\frac{7}{6} [f] + \frac{1}{6} [f'] (7 \beta - h)+ \frac{1}{6} [f''] (4 \beta ^2 - \frac{1}{2} (\beta + h)^2)\\&+ \frac{1}{6} [f'''] \left( \frac{4}{3} \beta ^3 - \frac{1}{6} (\beta + h)^3\right) , \quad \text { if } x<x^*\\ D^+(f_{n+1,3})=&\,\frac{4}{3}\left( -[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3\right) , \quad \text { if } x>x^*, \end{aligned} \end{aligned}$$
(28)

and for \(j=2\)

$$\begin{aligned} \begin{aligned} D^+(f_{n+2,3})=&\, 0, \quad \text { if } x>x^*\\ D^-(f_{n+2,3})=&\,[f] + [f'] (\beta + h) + \frac{1}{6} [f''] (3 \beta ^2 + 6 \beta h + 2 h^2)\\&+\frac{1}{6} [f''']\beta (\beta ^2 + 3 \beta h + 2 h^2), \quad \text { if } x<x^*, \end{aligned} \end{aligned}$$
(29)

with \(\alpha =x^*-x_n\) and \(\beta =x_{n+1}-x^*\).

Proof

Let us consider the four B-spline bases that appear in Fig. 2 and that contribute to the approximation in the interval \([x_n, x_{n+1}]\).

  • Let us consider \(j=-1\). From Fig. 2, we can clearly observe that \(L_3(f_{n-1,3})\) is correctly approximating in the interval \([x_n, x^*)\). Thus, \(C^-(f_{n-1,3}) = 0\). On the other hand, in the interval \((x^*, x_{n+1}]\), the approximation provided is not correct, as the operator \(L_3\left( f_{n-1,3}\right) \) uses information from the left of the discontinuity. Thus, the local truncation error can be calculated using Taylor expansions around \(x^*\). Proceeding in the same way as we did to obtain (10), we can write

    $$\begin{aligned} \begin{aligned} f_{n-2}^-&=f_{n-2}^+-[f]+[f'](2h+\alpha )-\frac{1}{2}[f''] (2h+\alpha )^2+\frac{1}{3!}[f'''] (2h+\alpha )^3+O(h^4),\\ f_{n-1}^-&=f_{n-1}^+-[f]+[f'](h+\alpha )-\frac{1}{2}[f''] (h+\alpha )^2+\frac{1}{3!}[f'''] (h+\alpha )^3+O(h^4),\\ f_{n}^-&=f_{n}^+-[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3+O(h^4),\\ \end{aligned} \end{aligned}$$
    (30)

    so the local truncation error introduced using \(L_3\left( f_{n-1,3}\right) \) in the interval \((x^*, x_{n+1}]\) can be obtained just replacing the expressions in (30):

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n-1,3}\right) =&\,\frac{4}{3}f_{n-1}^--\frac{1}{6}(f_{n-2}^-+f_{n}^-)\\ =&\,\frac{4}{3}\left( f_{n-1}^+-[f]+[f'](h+\alpha )-\frac{1}{2}[f''] (h+\alpha )^2+\frac{1}{3!}[f'''] (h+\alpha )^3+O(h^4)\right) \\&-\frac{1}{6}(f_{n-2}^+-[f]+[f'](2h+\alpha )-\frac{1}{2}[f''] (2h+\alpha )^2\\&+\frac{1}{3!}[f'''] (2h+\alpha )^3+O(h^4))\\&-\frac{1}{6}(f_{n}^+-[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3+O(h^4))\\ =&\,\frac{4}{3}f_{n-1}^+-\frac{1}{6}(f_{n-2}^++f_{n}^+)\\&+\Big (-[f] + [f'] (\alpha + h) - \frac{1}{6} [f''] (3 \alpha ^2 + 6 \alpha h + 2 h^2)\\&+\frac{1}{6} [f''']\alpha (\alpha ^2 + 3 \alpha h + 2 h^2)\Big ) +O(h^4)\\ =&\,\frac{4}{3}f_{n-1}^+-\frac{1}{6}(f_{n-2}^++f_{n}^+)+D^+(f_{n-1,3})+O(h^4). \end{aligned} \end{aligned}$$
    (31)

  • When \(j=2\), the local truncation error can be obtained in a symmetric way. In particular, in the interval \((x^*, x_{n+1}]\), \(L_3(f_{n+2,3})\) would be approximating correctly, while in the interval \([x_n, x^*)\), the local truncation error is

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n+2,3}\right) =&\,\frac{4}{3}f_{n+2}^+-\frac{1}{6}(f_{n+1}^++f_{n+3}^+)\\ =&\,\frac{4}{3}f_{n+2}^--\frac{1}{6}(f_{n+1}^-+f_{n+3}^-)\\&+\Big ([f] + [f'] (\beta + h) + \frac{1}{6} [f''] (3 \beta ^2 + 6 \beta h + 2 h^2)\\&+\frac{1}{6} [f''']\beta (\beta ^2 + 3 \beta h + 2 h^2)\Big ) +O(h^4)\\ =&\,\frac{4}{3}f_{n+2}^--\frac{1}{6}(f_{n+1}^-+f_{n+3}^-)+D^-(f_{n+2,3})+O(h^4). \end{aligned} \end{aligned}$$
    (32)

  • When \(j=0\), the local truncation error has to be considered in both intervals \([x_n, x^*)\) and \((x^*, x_{n+1}]\). Proceeding as before, for the approximation in the interval \([x_n, x^*)\), we can write that

    $$\begin{aligned} \begin{aligned} f_{n+1}^+&=f_{n+1}^-+[f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3+O(h^4), \end{aligned} \end{aligned}$$
    (33)

    Then, \(L_3\left( f_{n,3}\right) \) is

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n,3}\right)&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^+)\\&=\frac{4}{3}f_{n}^--\frac{1}{6} f_{n-1}^-\\&\quad -\frac{1}{6}\left( f_{n+1}^-+[f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3+O(h^4)\right) \\&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^-)\\&\quad +\left( -\frac{1}{6}\left( [f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3+O(h^4)\right) \right) \\&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^-)+D^-(f_{n,3})+O(h^4). \end{aligned} \end{aligned}$$
    (34)

    In the interval \((x^*, x_{n+1}]\), we have that

    $$\begin{aligned} \begin{aligned} f_{n-1}^-&=f_{n-1}^+-[f]+[f'](h+\alpha )-\frac{1}{2}[f''] (h+\alpha )^2+\frac{1}{3!}[f'''] (h+\alpha )^3+O(h^4),\\ f_{n}^-&=f_{n}^+-[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3+O(h^4),\\ \end{aligned} \end{aligned}$$
    (35)

    so \(L_3\left( f_{n,3}\right) \) is

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n,3}\right)&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^+)\\&=\frac{4}{3}\left( f_{n}^+-[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3\right) \\&\quad -\frac{1}{6}\left( f_{n-1}^+-[f]+[f'](h+\alpha )-\frac{1}{2}[f''] (h+\alpha )^2+\frac{1}{3!}[f'''] (h+\alpha )^3\right) \\&\quad -\frac{1}{6}f_{n+1}^+ +O(h^4)\\&=\frac{4}{3}f_{n}^+-\frac{1}{6}(f_{n-1}^++f_{n+1}^+)\\&\quad +\Big (-\frac{7}{6} [f] + \frac{1}{6} [f'] ( 7\alpha - h) - \frac{1}{6} [f''] (4 \alpha ^2 - \frac{1}{2} (\alpha + h)^2) \\&\quad + \frac{1}{6} [f'''] \left( \frac{4}{3} \alpha ^3 - \frac{1}{6} (\alpha + h)^3\right) \Big )+O(h^4)\\&=\frac{4}{3}f_{n}^+-\frac{1}{6}(f_{n-1}^++f_{n+1}^+)+D^+(f_{n,3})+O(h^4). \end{aligned} \end{aligned}$$
    (36)

  • The last case is symmetric to the first one. Again, the local truncation error has to be considered in both intervals \([x_n, x^*)\) and \((x^*, x_{n+1}]\). Thus, in the interval \([x_n, x^*)\), we can write that

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n+1,3}\right)&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n+1}^++f_{n+2}^+)\\&=\frac{4}{3}f_{n}^--\frac{1}{6}\Bigg (\left( f_{n+1}^-+[f]+[f']\beta +\frac{1}{2}[f''] \beta ^2+\frac{1}{3!}[f'''] \beta ^3+O(h^4)\right) \\&\quad +\left( f_{n+1}^-+[f]+[f'](\beta +h)+\frac{1}{2}[f''] (\beta +h)^2+\frac{1}{3!}[f'''] (\beta +h)^3+O(h^4)\right) \Bigg )\\&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^-)\\&\quad +\left( \frac{7}{6} [f] + \frac{1}{6} [f'] (7 \beta - h) + \frac{1}{6} [f''] (4 \beta ^2 - \frac{1}{2} (\beta + h)^2) \right. \\&\quad \left. + \frac{1}{6} [f'''] \left( \frac{4}{3} \beta ^3 - \frac{1}{6} (\beta + h)^3\right) \right) +O(h^4)\\&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n-1}^-+f_{n+1}^-)+D^-(f_{n+1,3})+O(h^4). \end{aligned} \end{aligned}$$
    (37)

    And in the interval \((x^*, x_{n+1}]\), we have that

    $$\begin{aligned} \begin{aligned} L_3\left( f_{n+1,3}\right)&=\frac{4}{3}f_{n}^--\frac{1}{6}(f_{n+1}^++f_{n+2}^+)\\&=\frac{4}{3}\left( -[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3+O(h^4)\right) -\frac{1}{6}(f_{n+1}^++f_{n+2}^+)\\&=\frac{4}{3}f_{n}^+-\frac{1}{6}(f_{n-1}^++f_{n+1}^+)\\&\quad +\frac{4}{3}\left( -[f]+[f']\alpha -\frac{1}{2}[f''] \alpha ^2+\frac{1}{3!}[f'''] \alpha ^3+O(h^4)\right) \\&=\frac{4}{3}f_{n}^+-\frac{1}{6}(f_{n-1}^++f_{n+1}^+)+D^+(f_{n+1,3})+O(h^4). \end{aligned} \end{aligned}$$
    (38)

\(\square \)

After this lemma, we define the following non-linear operator:

$$\begin{aligned} {\widetilde{L}}_3(f_{n+j,3})(x)=L_3(f_{n+j,3})+C^3_{n+j}(x) \end{aligned}$$
(39)

being

$$\begin{aligned} C^3_{n+j}(x)={\left\{ \begin{array}{ll} -D^{-}(f_{n+j,3}), &{} x^*\in [x_n,x_{n+1}], \quad x<x^*, \\ -D^{+}(f_{n+j,3}), &{} x^*\in [x_n,x_{n+1}], \quad x>x^*, \\ 0, &{} \text {in other case}, \end{array}\right. } \end{aligned}$$
(40)

with \(j=-1,0,1,2,\) and its associate operator:

$$\begin{aligned} {\mathcal {Q}}_3(f)(x)=\sum _{n\in {\mathbb {Z}}}{\widetilde{L}}_3(f_{n,3})(x)B_3\left( \frac{x}{h}-n\right) . \end{aligned}$$
(41)

Now, we can easily give a proof for the following theorem:

Theorem 2

Let us consider \(n_0\in {\mathbb {Z}}\) and a finite interval I with \([x_{n_0}, x_{n_0+1}]\subset I\). If there exists a singularity placed at \(x^*\) in the interval \([x_{n_0}, x_{n_0+1}]\), then

$$\begin{aligned} ||{\mathcal {Q}}_3(f)-f||_{\infty ,I}=O(h^4). \end{aligned}$$

Proof

As in the previous section, the proof is straightforward if we have a look to the expressions of the local truncation error in (31), (32), (34), (36), (37), and (38). \(\square \)

Remark 1

Similar considerations can be taken here regarding the accuracy needed for the jump relations in (8) (as in Corollary 1). But the conclusions are similar: the accuracy needed is \(O(h^4)\) for [f], \(O(h^3)\) for \([f']\), and so on.

Remark 2

Using the same reasoning as in Corollary 2, the accuracy needed for the approximation of the location of the discontinuity (if we do not know it) must be \(O(h^4)\) for cubic splines.

Remark 3

As considered in Corollary 3, the error of the corrected cubic spline is smooth and retains the smoothness of the B-splines bases. Just having a look to the expressions of the error in (26), (27), (28) and (29), it is clear that the error of the spline before or after the correction retains the smoothness of the B-splines bases.

Remark 4

As mentioned at the beginning of Sect. 2, the extension of the techniques presented in this article to data given in the cell-averages setting is straightforward considering the primitive function (Aràndiga and Donat 2000), which is a function given in the point values.

4 The new method in higher dimensions

In this section, we want to discuss how to extend the results presented in previous sections to higher dimensions using tensor product. We have selected the tensor product approach because it intuitively extends the results of B-splines from one dimension and it is widely used. This method takes advantage of the separable way in which we can write spline bases in multiple dimensions. However, this approach may pose challenges if discontinuities are not handled with care. There are non-separable methods in the literature for approximating multivariate functions with discontinuities in different contexts, see for example, the discussion about this topic introduced in Mateï and Meignen (2015), Arandiga et al. (2008), and Arandiga et al. (2010). In what follows, the reader can find more details about the mentioned extension using tensor product.

Let be \(1\le k\in {\mathbb {N}}\), an open set \(\Omega \subseteq {\mathbb {R}}^k\) and a function \(f:{\mathbb {R}}^k\rightarrow {\mathbb {R}}\) with \(f\in {\mathcal {C}}^l({\mathbb {R}}^k)\). We suppose \(h>0\), \({\textbf{n}}=(n_1,\ldots ,n_k)\in {\mathbb {Z}}^k\) and consider

$$\begin{aligned} \begin{aligned}&f_{{\textbf{n}}}=f(n_1h,\ldots ,n_k h),\\&f_{{\textbf{n}},3}=\{f_{(n_1+j_1,\ldots ,n_k+j_k)}=f(n_1h+j_1h,\ldots ,n_kh+j_kh): \,\, |j_s| \le 1,\,\, s=1,\ldots ,k \}. \end{aligned} \end{aligned}$$
(42)

With this notation, we define the tensor product of the operator \(L_p\) with \(p=2,3\), Eq. (5), as

$$\begin{aligned} \begin{aligned} L_{\textbf{p}}(f_{{\textbf{n}},3})=&\,L_{(p_1,\ldots ,p_k)}(f_{{\textbf{n}},3})=\sum _{j_1=-1}^1\ldots \sum _{j_k=-1}^1 c^{p_1}_{j_1}\ldots c^{p_k}_{j_k}f_{(n_1+j_1,\ldots ,n_k+j_k)}, \end{aligned} \end{aligned}$$

with \({\textbf{p}}=(p_1,\ldots ,p_k)\in \{2,3\}^k\) since \(L_p\) is linear. For example if \(k=2\) and \({\textbf{p}}=(p,p)\), then

$$\begin{aligned} \begin{aligned} L_{(p,p)}(f_{{\textbf{n}},3})=&\,L_{(p,p)}(f_{(n_1,n_2),3})=\sum _{j_1=-1}^1\sum _{j_2=-1}^1 c^{p}_{j_1}c^{p}_{j_2}f_{(n_1+j_1,n_2+j_2)}\\ =&\,\sum _{j_1=-1}^1 c^{p}_{j_1}\left( c^p_{-1}f_{(n_1-1,n_2+j_2)}+c^p_0f_{(n_1,n_2+j_2)}+c^p_1f_{(n_1+1,n_2+j_2)}\right) \\ =&\,c^p_{-1}\left( c^p_{-1}f_{(n_1-1,n_2-1)}+c^p_0f_{(n_1,n_2-1)}+c^p_1f_{(n_1+1,n_2-1)}\right) +\\&+c^p_{0}\left( c^p_{-1}f_{(n_1-1,n_2)}+c^p_0f_{(n_1,n_2)}+c^p_1f_{(n_1+1,n_2)}\right) +\\&+c^p_{1}\left( c^p_{-1}f_{(n_1-1,n_2+1)}+c^p_0f_{(n_1,n_2+1)}+c^p_1f_{(n_1+1,n_2+1)}\right) . \end{aligned} \end{aligned}$$

Thus, if \(p=2\), we get

$$\begin{aligned} \begin{aligned} L_{(2,2)}(f_{{\textbf{n}},3})=&\,-\frac{1}{8}\left( -\frac{1}{8}f_{(n_1-1,n_2-1)}+\frac{5}{4}f_{(n_1,n_2-1)}-\frac{1}{8}f_{(n_1+1,n_2-1)}\right) +\\&+\frac{5}{4}\left( -\frac{1}{8}f_{(n_1-1,n_2)}+\frac{5}{4}f_{(n_1,n_2)}-\frac{1}{8}f_{(n_1+1,n_2)}\right) +\\&-\frac{1}{8}\left( -\frac{1}{8}f_{(n_1-1,n_2+1)}+\frac{5}{4}f_{(n_1,n_2+1)}-\frac{1}{8}f_{(n_1+1,n_2+1)}\right) \\ =&\,\frac{1}{64}f_{(n_1-1,n_2-1)}-\frac{5}{32}f_{(n_1,n_2-1)}+\frac{1}{64}f_{(n_1+1,n_2-1)}+ -\frac{5}{32}f_{(n_1-1,n_2)}\\&\quad \ +\frac{25}{16}f_{(n_1,n_2)}\\&-\frac{5}{32}f_{(n_1+1,n_2)}+\frac{1}{64}f_{(n_1-1,n_2+1)}-\frac{5}{32}f_{(n_1,n_2+1)}+\frac{1}{64}f_{(n_1+1,n_2+1)}. \end{aligned} \end{aligned}$$
(43)

and if \(p=3\), we obtain

$$\begin{aligned} \begin{aligned} L_{(3,3)}(f_{{\textbf{n}},3})=&\,\frac{1}{36}f_{(n_1-1,n_2-1)}-\frac{2}{9}f_{(n_1,n_2-1)}+\frac{1}{36}f_{(n_1+1,n_2-1)}+ -\frac{2}{9}f_{(n_1-1,n_2)}+\frac{16}{9}f_{(n_1,n_2)}\\&-\frac{2}{9}f_{(n_1+1,n_2)}+\frac{1}{36}f_{(n_1-1,n_2+1)}-\frac{2}{9}f_{(n_1,n_2+1)}+\frac{1}{36}f_{(n_1+1,n_2+1)}. \end{aligned} \end{aligned}$$
(44)

Let us start by expressing (4) in several dimensions:

$$\begin{aligned} Q_{\textbf{p}}(f)({\textbf{x}})=\sum _{{\textbf{n}}\in {\mathbb {Z}}^k}L_{\textbf{p}}\left( f_{{\textbf{n}},3}\right) B_{\textbf{p}}\left( \frac{{\textbf{x}}}{h}-{\textbf{n}}\right) , \end{aligned}$$
(45)

with

$$\begin{aligned} B_{\textbf{p}}\left( \frac{{\textbf{x}}}{h}-{\textbf{n}}\right) =\prod _{j=1}^k B_{p_j}\left( \frac{x_j}{h}-n_j\right) . \end{aligned}$$

In particular, if \(k=2\) and \({\textbf{p}}=(p,p)\), we get

$$\begin{aligned} Q_{(p,p)}(f)(x_1,x_2)=\sum _{n_2,n_1\in {\mathbb {Z}}}L_{(p,p)}\left( f_{(n_1,n_2),3}\right) B_{p}\left( \frac{x_1}{h}-n_1\right) B_{p}\left( \frac{x_2}{h}-n_2\right) . \end{aligned}$$
(46)

It is clear that this construction allows to use the correction terms presented in Sects. 2 and 3 by rows and by columns. In this case, as the correction is applied dimension by dimension, the unidimensional algorithm presented in Aràndiga et al. (2005) can still be used. We define the following operation between two non-linear \({\widetilde{L}}_p\) operators:

Definition 1

Let \({\widetilde{L}}_{p_1},{\widetilde{L}}_{p_2}\) be two operators defined in Eqs. (23) and (39), with \(p_1,p_2=2,3\), let \({\textbf{n}}\in {\mathbb {Z}}^2\) and \(f_{{\textbf{n}},3}=(f_{(n_1+j_1,n_2+j_2)})_{j_1,j_2=-1}^1\), then we define the product:

$$\begin{aligned} \begin{aligned}&{\widetilde{L}}_{p_2}\otimes {\widetilde{L}}_{p_1}(f_{{\textbf{n}},3})(x_1,x_2)=\sum _{j_2=-1}^1\left( c^{p_2}_{j_2}{\widetilde{L}}_{p_1}(f_{n_1,3,n_2+j_2})(x_1)+C^{p_2}_{(n_1,n_2+j_2)}(x_2)\right) \\ \end{aligned} \end{aligned}$$
(47)

where \(f_{n_1,3,n_2+j_2}=(f_{(n_1-1,n_2+j_2)},f_{(n_1,n_2+j_2)},f_{(n_1+1,n_2+j_2)})\) and \(C_{(k_1,k_2)}(x_i)\) are the corrections terms obtained in Lemmas 1 and 2, applied over the variable \(x_i\), \(i=1,2\).

For example, if \(p_1=p_2=2\), then

$$\begin{aligned} \begin{aligned}&{\widetilde{L}}_{2}\otimes {\widetilde{L}}_{2}(f_{{\textbf{n}},3})(x_1,x_2)=\sum _{j_2=-1}^1\left( c^{2}_{j_2}{\widetilde{L}}_{p_1}(f_{n_1,3,n_2+j_2})(x_1)+C^{2}_{(n_1,n_2+j_2)}(x_2)\right) \\&\quad =\frac{5}{4}{\widetilde{L}}_{p_1}(f_{n_1,3,n_2})(x_1)-\frac{1}{8}({\widetilde{L}}_{p_1}(f_{n_1,3,n_2-1})(x_1)+{\widetilde{L}}_{p_1}(f_{n_1,3,n_2+1})(x_1))\\&\qquad +C^{2}_{(n_1,n_2)}(x_2)+C^{2}_{(n_1,n_2-1)}(x_2)+C^{2}_{(n_1,n_2+1)}(x_2)\\&\quad =\frac{5}{4}\left( \frac{5}{4}f_{(n_1,n_2)}-\frac{1}{8}(f_{(n_1-1,n_2)}+f_{(n_1+1,n_2)})+C^2_{(n_1,n_2)}(x_1)\right) \\&\qquad -\frac{1}{8}\left( \frac{5}{4}f_{(n_1,n_2-1)}-\frac{1}{8}(f_{(n_1-1,n_2-1)}+f_{(n_1+1,n_2-1)})+C^2_{(n_1,n_2-1)}(x_1)\right) \\&\qquad -\frac{1}{8}\left( \frac{5}{4}f_{(n_1,n_2+1)}-\frac{1}{8}(f_{n_1-1,n_2+1)}+f_{(n_1+1,n_2+1)})+C^2_{(n_1,n_2+1)}(x_1)\right) \\&\qquad +C^{2}_{(n_1,n_2)}(x_2)+C^{2}_{(n_1,n_2-1)}(x_2)+C^{2}_{(n_1,n_2+1)}(x_2).\\ \end{aligned} \end{aligned}$$
(48)

Definition 1 can be extended using recursively the next relation:

$$\begin{aligned} {\widetilde{L}}_{p_3}\otimes {\widetilde{L}}_{p_2}\otimes {\widetilde{L}}_{p_1}(f_{{\textbf{n}},3}):={\widetilde{L}}_{p_3}\otimes \left( {\widetilde{L}}_{p_2}\otimes {\widetilde{L}}_{p_1}\right) (f_{{\textbf{n}},3}). \end{aligned}$$

At this point, we can design a version of \({\widetilde{L}}_p\) in several dimensions. We take into account that the operator is non-linear, it depends on the points where the discontinuity is. Let \({\textbf{x}}=(x_1,\ldots ,x_k)\in {\mathbb {R}}^k\) be a point, then

$$\begin{aligned} \begin{aligned}&{\widetilde{L}}_{\textbf{p}}(f_{{\textbf{n}},3})({\textbf{x}})={\widetilde{L}}_{(p_1,\ldots ,p_k)}(f_{{\textbf{n}},3})({\textbf{x}})={\widetilde{L}}_{p_k}\otimes \cdots \otimes {\widetilde{L}}_{p_1}(f_{{\textbf{n}},3})({\textbf{x}}).\\ \end{aligned} \end{aligned}$$
(49)

Finally, the new non-linear spline in several dimensions based on B-splines is the following:

$$\begin{aligned} {\mathcal {Q}}_{\textbf{p}}(f)({\textbf{x}})=\sum _{{\textbf{n}}\in {\mathbb {Z}}^k}{\widetilde{L}}_{\textbf{p}}\left( f_{{\textbf{n}},3}\right) ({\textbf{x}})B_{\textbf{p}}\left( \frac{{\textbf{x}}}{h}-{\textbf{n}}\right) . \end{aligned}$$
(50)

In particular, if \(k=2\) and \({\textbf{p}}=(p,p)\), we get

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{(p,p)}(f)(x_1,x_2)&=\sum _{n_2,n_1\in {\mathbb {Z}}}{\widetilde{L}}_{(p,p)}(x_1,x_2)\left( f_{(n_1,n_2),3}\right) B_{p}\left( \frac{x_1}{h}-n_1\right) B_{p}\left( \frac{x_2}{h}-n_2\right) \\&=\sum _{n_2,n_1\in {\mathbb {Z}}}{\widetilde{L}}_{p}\otimes {\widetilde{L}}_{p}(f_{{\textbf{n}},3})(x_1,x_2)B_{p}\left( \frac{x_1}{h}-n_1\right) B_{p}\left( \frac{x_2}{h}-n_2\right) . \end{aligned} \end{aligned}$$
(51)

The processing can be done either by rows and then by columns or the other way around with similar results. From the expression in (48), we can see that we have chosen the first option. We can easily extend this result to any number of dimensions.

Now, we can discuss about the location of the singularity curve in several dimensions. For bivariate piecewise smooth functions, the interface where the singularity occurs is a curve in the plane. For trivariate functions, it is a surface in the space, etc. An accurate representation of the interface is still needed to obtain a reconstruction of the data with high order of accuracy. This representation can be done using a level set function. In this article we suppose that we have a level set function through which we can locate the position of the singularity curve.

4.1 Discussion about how to locate the singularity using a level set surface in 2D

The location of the singularity in one-dimensional problems is a subject that has been already discussed in the literature, see for example (Aràndiga et al. 2005) and the references therein. About how to keep track of the location of the discontinuity in several dimensions, several approaches can also be found in the literature in other contexts, see for example (Mateï and Meignen 2015; Arandiga et al. 2008, 2010; Floater et al. 2014; Romani et al. 2019; Allasia et al. 2009; Bozzini and Rossini 2000, 2013; Gout et al. 2008; Bracco et al. 2019) and the references therein. In the context of our multivariate data approximation, we have followed two approaches. If we have a look to the local truncation errors in Lemma 1 for quadratic splines or for those in Lemma 2 for cubic splines, we can see that the distance \(\beta \), i.e. the location of the discontinuity, needs to be approximated (in the case it is unknown) with \(O(h^3)\) accuracy for quadratic splines or \(O(h^4)\) for cubic splines, if we do not want to affect the accuracy of the spline approximation close to the discontinuity. If a level set function \(\varphi (\textbf{x})\) is used to locate the singularity, a simple one-dimensional approach can be followed to obtain the distance to the discontinuity from singular points (we consider singular points, those central points of the operator \(L_p\) in (4) for which the support of \(L_p\) crosses the discontinuity). This approach has been described in the context of the numerical approximation of the solution of PDEs with interfaces (see, e.g. Leveque and Li 1994; Li and Ito 2006). It is based on Taylor expansions and it is enough to obtain approximations of \(\alpha \) with \(O(h^3)\) accuracy in Lemma (1). Particularising the explanation in Leveque and Li (1994) and Li and Ito (2006) to one dimension, we can suppose that x is a grid point near the interface, then the position of the interface is \(x^*=x+\beta \). Since x is close to the interface, \(\beta \) is small and we can use Taylor’s expansion on the level set function \(\varphi (x)\) that is regular. Thus, writing \(\varphi (x^*)=\varphi (x+\beta )=0\), we get a second-order equation for the distance \(\beta \),

$$\begin{aligned} \varphi (x)+\varphi _x(x)\beta +\frac{1}{2}\varphi _{xx}(x)\beta ^2=0. \end{aligned}$$
(52)

As the level set function is smooth, the order of accuracy for \(\beta \) is \(O(h^3)\) if the approximation of the derivatives is obtained using the standard five points stencil. This approach is valid for quadratic splines (as an approach of \(O(h^3)\) accuracy for \(\beta \) is enough). For cubic splines, other approach is needed: either to add another term in the expansion to (52) and use some Newton’s iterations to solve the equation, or try other possibilities. For example, assuming that we are still using a level set function for locating the position of the discontinuity curve, we can always obtain the absolute value of the level set to obtain a kink placed over the discontinuity curve. Then, we can use the algorithm in Aràndiga et al. (2005) to obtain accurate approximations of the location of the discontinuity in the x direction or the y direction. Both approaches present problems close to the boundary of the domain, so we need to assume that there is a belt of some points all along the boundary of the domain where we cannot obtain an accurate approximation.

4.2 Process to approximate data in several dimensions

In this subsection, we explain the steps that we need to follow in order to approximate data in several dimensions:

  1. 1.

    We start from multivariate data at a low resolution, and a level set function which zero level set locates the position of the discontinuity.

  2. 2.

    We select one dimension of the data.

  3. 3.

    We process the data in the dimension selected using the unidimensional quadratic or cubic spline plus correction terms described in the previous sections.

  4. 4.

    We interpolate the level set function in the dimension selected (remind that it is a smooth function), for example, using the same quadratic or cubic spline interpolation (without correction terms), respectively. In order to improve computational cost, we can store and interpolate the level set within a wide enough tube around the discontinuity curve.

  5. 5.

    If there are no more dimensions to compute, we finish the process. Otherwise, we select another dimension of the data and go to step 3.

5 Numerical experiments

In this section, we present plots of the reconstructions obtained through classical and corrected quadratic and cubic splines. We will also present grid refinement experiments that aim to support the theoretical results obtained about the accuracy of the new algorithm. To do so, we start from data obtained from the sampling of a piecewise smooth function. The location of the discontinuity is considered known in the case of jump discontinuities in the function, but we will be able to approximate its location when the jumps are in the first-order derivative. In this case, we trust the approximation of the location of the singularity to the algorithm presented in Aràndiga et al. (2005).

For the grid refinement analysis, we obtain the infinity norm \(E^l=||f^l-\tilde{f^l}||_{L^\infty }\) over the domain, where l represents the step of the refinement process, which consists in reducing the grid size h to h/2 when going from l to \(l+1\). Once the error has been computed, the numerical accuracy can be obtained through the classical formula:

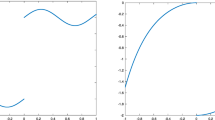
$$\begin{aligned} O^l= \log _2\left( \frac{E^l}{E^{l+1}}\right) . \end{aligned}$$

For the univariate numerical experiments, we consider the piecewise continuous function presented in (53):

$$\begin{aligned} f(x)=\left\{ \begin{array}{ll} -20 x^4+x^3+5 x^2+x, &{} \text { if } 0\le x<0.5,\\ 4 x^4+x^3+x^2-x+2, &{} \text { if } 0.5\le x\le 1, \end{array} \right. \end{aligned}$$
(53)

and the one in (54):

$$\begin{aligned} f(x)=|\cos (\pi x)|. \end{aligned}$$
(54)
Fig. 3
figure 3

Function in (53) and (54) used in the numerical experiments

Full size image

Both cases are presented in Fig. 3. In the first case, the function presents a jump discontinuity at \(x=0.5\), so we assume that the location of the discontinuity is known, but the jump in the function and the derivatives are obtained with enough accuracy using one-sided interpolation (Amat et al. 2018). For the second case, the function presents jumps in the derivatives at \(x=0.5\), but it is continuous, so the location of the singularity can be approximated using, for example, the algorithm in Aràndiga et al. (2005). As in the previous case, the jumps in the function and the derivatives can be also approximated using one-sided interpolation.

5.1 A first experiment with a function that presents a jump discontinuity

Let us start by the function presented in Fig. 3 to the left. It corresponds to the function in (53). In Fig. 4, we present the result obtained when approximating a sampling of 32 initial points of this function, using the classical quadratic (first and second rows) and cubic (third and fourth rows) splines with (left) and without corrections (right). Rows one and three show the approximation and rows two and four show the absolute value of the error. For these experiments, we have approximated 10 uniform points between the initial data nodes for the cubic spline and 11 uniform points for the quadratic.

Fig. 4
figure 4

In the first row of the figure, we can observe the approximation of the function in (53) using 32 initial points through the corrected quadratic spline (left) and the classical quadratic spline (right). The second row shows the absolute error for each one of the splines. The third and fourth rows show the same results obtained by the corrected cubic spline (left) and the classical one (right)

Full size image

We can see that the corrections allow to improve the accuracy of the reconstruction close to the singularity. Let us now analyse if the full order of accuracy (meaning \(O(h^3)\) accuracy for the quadratic spline and \(O(h^4)\) for the cubic one) is recovered. To do so, we present the results of a grid refinement experiment in Table 1. We can see that the numerical accuracy supports the theoretical results obtained in Theorems 1 and 2. We have also represented these results in a semilogarithmic scale in Fig. 5 to show the decreasing of the error, so that we can compare it with the theoretical results. To the left of this figure, we can observe the result of the quadratic spline, and to the right, the result of the cubic spline. In both plots, we present with red stars the errors in the infinity norm obtained by the classical spline, and with blue stars, the error of the corrected one. We have represented with dashed lines the theoretical decreasing of the error, which corresponds to O(1) accuracy for classical splines, \(O(h^3)\) for corrected quadratic splines and \(O(h^4)\) for corrected cubic splines.

Table 1 Grid refinement analysis for the accuracy of the corrected and classical splines using the infinity norm at the high-resolution nodes
Full size table
Fig. 5
figure 5

Representation of the results of the grid refinement analysis for the numerical accuracy obtained for quadratic (left) and cubic (right) splines and presented in Table 1. The original data come from the function in (53). The error has been represented in a semilogarithmic scale so that we can appreciate the decreasing of the error. In both plots, we can observe, represented in red stars, the errors in the infinity norm obtained by the classical spline, and with blue stars, the error of the corrected one. We have represented with dashed lines the theoretical decreasing of the error

Full size image

5.2 A second experiment with a piecewise smooth function that presents a jump at least in the first derivative

In this second experiment, we will use data that comes from the sampling of the function in (54). This function presents a jump in the first (and higher) order derivatives. In this case, we trust in the algorithm proposed in Aràndiga et al. (2005) for the location of the singularity. As in the previous experiment, the jumps in the function and the derivatives are approximated using one-sided interpolation (Amat et al. 2018). Figure 6 shows the results obtained when approximating a sampling of 32 initial points of the function in (54), using the classical quadratic (first and second rows) and cubic (third and fourth rows) splines with (left) and without corrections (right). Rows one and three show the approximation and rows 2 and 4 show the absolute value of the error. As we did in the previous experiment, we have approximated 10 uniform points between the initial data nodes for the cubic spline and 11 uniform points for the quadratic.

Table 2 and Fig. 7 present the results of a grid refinement analysis in the infinity norm. The conclusions that can be reached are similar to the ones obtained in previous experiment: Even in the presence of singularities, the corrected splines recover the accuracy of the spline at smooth zones in the infinity norm.

Fig. 6
figure 6

In the first row of the figure, we can observe the approximation of the function in (53) using 32 initial points through the corrected quadratic spline (left) and the classical quadratic spline (right). The second row shows the absolute error for each one of the splines. The third and fourth rows show the same results obtained by the corrected cubic spline (left) and the classical one (right)

Full size image
Table 2 Grid refinement analysis for the accuracy of the corrected and classical splines using the infinity norm at the high-resolution nodes
Full size table
Fig. 7
figure 7

Representation of the results of the grid refinement analysis for the numerical accuracy obtained for quadratic (left) and cubic (right) splines and presented in Table 2. The original data comes from the function in (54). The error has been represented in a semilogarithmic scale so that we can appreciate the decreasing of the error. In both plots we can observe, represented in red stars, the errors in the infinity norm obtained by the classical spline, and with blue stars, the error of the corrected one. We have represented with dashed lines the theoretical decreasing of the error

Full size image

5.3 A third experiment for the approximation of a bivariate function using a cubic spline

We dedicate this subsection to present an experiment for the approximation of a bivariate function using the corrected cubic spline (results for quadratic splines allow to obtain similar conclusions). We set the level set function

$$\begin{aligned} \varphi (x,y)=x^2+y^2-r^2, \end{aligned}$$
(55)

with \(r=0.5\) and \(0\le x\le 1\), \(0\le y\le 1\). The function presents a jump, so we use the level set function to track the position of the singularity using the first algorithm explained in Sect. 4.1. To obtain the results in several dimensions, we apply the extension of the algorithm introduced in Sect. 4. To check the numerical accuracy, we perform a grid refinement analysis in the infinity norm for the next bivariate function,

$$\begin{aligned} f(x,y)=\left\{ \begin{array}{ll} x^4+y^4, &{} \text { if } \varphi (x,y)\le 0,\\ x^3+y^3+5, &{} \text { if } \varphi (x,y)>0. \end{array} \right. \end{aligned}$$
(56)

The results are presented in Table 3. We can see how the new technique keeps the numerical order of accuracy of the cubic spline at smooth zones in the infinity norm. The classical spline introduces oscillations and smearing close to the discontinuity curve, so it can not conserve the accuracy. In Fig. 8, we can see the reconstruction (in the first row of the figure) and the error (in the second row) obtained by the cubic spline in 2D plus correction terms (first column) and without correction terms (second column). The colour bars in the two figures of the error allow to appreciate the size of the error, which is mainly placed around the discontinuity curve.

Table 3 Grid refinement analysis for the accuracy of the corrected and classical cubic splines using the infinity norm at the high resolution nodes
Full size table
Fig. 8
figure 8

In the first row of the figure, we can observe the approximation of the function in (56) using \(128\times 128\) initial nodes through the corrected cubic spline (left) and the classical cubic spline (right). We approximate at 10 equidistant positions between every two nodes in each dimension, which results in a final resolution of \(1398\times 1398\). The second row shows the absolute error for each one of the splines. The colour bar in this las two figures allows to appreciate the size of the error, mainly placed over the discontinuity curve

Full size image

6 Conclusions

In this article, we have presented a new algorithm that allows for the approximation of piecewise smooth functions with full accuracy using cubic and quadratic splines. By full accuracy, we mean the accuracy of the spline at smooth zones. The algorithm is based on the computation of simple correction terms that can be added to the approximation obtained by the classical cubic or quadratic splines. We have given proofs for the accuracy of the approximation obtained through the new algorithm. Through a tensor product strategy, we have extended the one-dimensional results to any number of dimensions. The numerical experiments presented show that the reconstructions are piecewise smooth and that they conserve the accuracy of the splines at smooth zones even close to the singularities. The analysis of the numerical accuracy in the infinity norm supports the theoretical results obtained in one and two dimensions.