1 Introduction

Optimization problems arising from allocation of resources or apportionment of goods often contain conditions on the feasibility of a solution which are best represented by a graph. In particular, incompatibilities between pairs of objects can be modeled in a natural way by means of a conflict graph. There is a wide range of literature where conflict graphs are added to combinatorial optimization problems leading to new problems with feasible solutions consisting of objects whose graph representations are independent sets in the conflict graph, e.g., knapsack problems (Pferschy and Schauer 2009, 2017), bin packing (Muritiba et al. 2010), scheduling (e.g., Bodlaender and Jansen (1993); Even et al. (2009)), transportation (Santos et al. 2019), and problems on graphs (e.g., Darmann et al. (2011)).

In general, optimizing over independent sets will make most optimization problems computationally hard. Therefore, a widely pursued research direction consists in the identification of special graph classes where the implied optimization problem exhibits a more benevolent behavior.

We consider a very natural allocation problem where a set of n indivisible goods or items has to be distributed among k agents. Each agent has his or her own profit function over the set of items. The profits of items are additive. To obtain a fair allocation of items, the minimal total profit obtained by any of the agents should be maximized. Such a maxi–min criterion is probably the most natural fairness measure and can be found frequently in Computational Social Choice. This problem is well known as the Santa Claus problem (see Bansal and Sviridenko 2006) where presents (items) should be distributed to kids (agents) so that even the least happy kid is as happy as possible. It is easy to see by a reduction from Partition that this problem is weakly NP-hard already for \(k=2\), even if all k profit functions are identical. Thus, the best we can hope for, from a computational complexity point of view, are pseudo-polynomial algorithms for restricted classes of input instances.

We consider restrictions on input instances giving rise to special classes expressed in terms of properties of the corresponding conflict graph permitting an incompatibility relation between pairs of items. Two vertices are joined by an edge if the two corresponding items do not fit together well, e.g., being substitutes for each other. In the resulting optimization problem, we are looking for the most fair solution where the allocation to every agent constitutes an independent set in the conflict graph.

In the present paper, we continue the line of research started in our previous work (Chiarelli et al. 2023) where the fair allocation problem with conflicts was first introduced and motivated, and the relation to existing literature was laid out in detail. In that paper, several graph classes were classified as belonging to one of the two sides of the complexity divide, i.e., the problem, when restricted to graphs from the class, is either strongly NP-hard or permits a pseudo-polynomial algorithm. In the current paper, we add three highly relevant types of graphs to the positive side and, thus, proceed to narrow the gap between hard and tractable cases. As in the previous paper (Chiarelli et al. 2023), we consider the number of agents k as a constant.

Obviously, the fair division problem with conflicts coincides with the strongly NP-hard Weighted Independent Set problem (WIS) for the case of a single agent (\(k=1\)). Thus, it only makes sense to consider graph classes where WIS can be solved in polynomial time. This immediately points to perfect graphs (Grötschel et al. 1988). However, our allocation problem was shown to be strongly NP-hard for several subclasses of perfect graphs as conflict graphs (Chiarelli et al. 2023), among them the prominent class of bipartite graphs. On the positive side, we could show that biconvex bipartite graphs still permit pseudo-polynomial solution algorithms. In this paper, we manage to push the bar further up by presenting a fairly involved pseudo-polynomial time algorithm for convex bipartite graphs (see Sect. 1.2 for definitions).

Outside the area of perfect graphs, we construct pseudo-polynomial algorithms for conflict graphs of bounded clique-width or bounded tree-independence number. Both of these results extend the only previously known cases of tractable non-perfect graphs, namely graphs of bounded treewidth.

1.1 Problem statement and results

For a formal definition of our problem, let V be a set of items with \(|V|=n\), let k be a positive integer, and let \(p_1,\ldots ,p_k: V \rightarrow {\mathbb {Z}}_+\) be k profit functions. An ordered k-partition of V is a sequence \((X_1,\ldots ,X_k)\) of k pairwise disjoint subsets of V such that \(\bigcup _{i = 1}^k X_i = V\). Given profit functions \(p_1,\dots , p_k\), the satisfaction level of an ordered k-partition \((X_1,\ldots ,X_k)\) of V is defined as the minimum over the k individual profits \(p_j(X_j) {:}{=} \sum _{v\in X_j}p_j(v)\), \(j\in \{1,\ldots , k\}\). The standard fair division problem is defined as follows.

figure a

A conflict graph \(G = (V,E)\) on the set V of items represents incompatibilities between pairs of items. If two items i and j are joined by an edge \(\{i,j\} \in E\), then i and j should not be included in the same subset of the partition. Conflict-free allocation of items immediately leads to (partial) colorings of the conflict graph (cf. Berge (1989) and de Werra (1989)).

Definition 1

A partial k-coloring of a graph G is a sequence \((X_1,\ldots ,X_k)\) of k pairwise disjoint independent sets in G.

Obviously, any partial k-coloring of a graph G corresponds to a k-division of the items respecting the incompatibilities, since every set in the partition is an independent set in G. Note that an optimal partial k-coloring \((X_1,\ldots ,X_k)\) does not necessarily select all vertices from V, i.e., some items may remain unassigned (which can be ruled out for the problem without conflict relations). Taking the k profit functions into account we can define for each partial k-coloring \(c = (X_1,\ldots , X_k)\) of a graph G a k-tuple \((p_1(X_1),\ldots , p_k(X_k))\) as the profit profile of c. Then, the satisfaction level of c is given by \(\min _{j=1}^k \{p_j(X_j)\}\), i.e., the minimum profit of a profile. In this paper, the following resulting optimization problem is considered:

figure b

We will also refer to the decision version of the problem: given a target value \(q \in {\mathbb {Z}}_+\), does there exist a partial k-coloring of G with satisfaction level at least q?

Even without conflicts the plain problem Fair k -Division of Indivisible Items is weakly NP-hard for any constant \(k\ge 2\) and strongly NP-hard for k being part of the input. This holds even for k identical profit functions (see the discussion in Chiarelli et al. 2023). Thus, pseudo-polynomial algorithms for Fair k-Division Under Conflicts can only be developed for constant k.

In our preceding paper (Chiarelli et al. 2023), we derived the following results.Footnote 1 The decision version of Fair k-Division Under Conflicts is strongly NP-complete for any fixed \(k\ge 2\) if the conflict graph is a bipartite graph or a line graph of a bipartite graph. Both results imply that the problem is hard on perfect graphs, where Weighted Independent Set is still polynomial.

On the other hand, we established pseudo-polynomial solution algorithms for the following graph classes: biconvex bipartite graphs, cocomparability graphs, chordal graphs, and graphs of bounded treewidth.

It was also shown that all these algorithms, which rely on dynamic programs of pseudo-polynomial size, permit the construction of fully polynomial time approximation schemes (FPTAS).

In this paper, we give, for any fixed positive integer k, a pseudo-polynomial algorithm for Fair k-Division Under Conflicts in the class of convex bipartite graphs in Sect. 2, thereby answering a question from Chiarelli et al. (2023). Note that this approach is completely different from the previous algorithm for the biconvex bipartite case. Secondly, we construct a pseudo-polynomial algorithm for Fair k-Division Under Conflicts on conflict graphs of bounded clique-width in Sect. 3. Since graph classes of bounded treewidth have bounded clique-width but not vice versa, this is a strict generalization of the analogous result on bounded treewidth from Chiarelli et al. (2023). Third, we provide another generalization of the result for bounded treewidth, which at the same time also generalizes the solution for chordal graphs, by adapting the bounded treewidth algorithm to graphs with bounded tree-independence number in Sect. 4.

The presented algorithms explore the structural properties of the respective graph classes to generate suitable sets of profit profiles as states in a dynamic programming approach. By the same reasoning as in Section 4 of Chiarelli et al. (2023), we can also conclude that each of the dynamic programming algorithms laid out for convex bipartite graphs, graphs of bounded clique-width, and graphs of bounded tree-independence number also leads to a fully polynomial time approximation scheme (FPTAS).

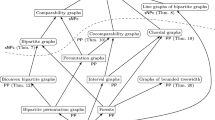
Pointing out further open questions, we would like to mention \(\chi \)-bounded graph classes (see, e.g., Scott and Seymour 2020), which are graph classes \({\mathcal {G}}\) closed under induced subgraphs for which there exists a function f bounding from above the chromatic number of each graph \(G\in {\mathcal {G}}\) in terms of its clique number. These can be seen as a simultaneous extension of the class of perfect graphs, as well as of graph classes of bounded clique-width (see Dvořák and Král’ 2012) and graphs of bounded tree-independence number (see Dallard et al. 2022a). Narrowing the gap of computational complexity between \(\chi \)-bounded graph classes and graphs of bounded clique-width, resp. bounded tree-independence number, would be an interesting challenge. An overview of the state of knowledge for various graph classes is given in Fig. 1.

Fig. 1
figure 1

Relationships between various graph classes and the complexity of Fair k-Division Under Conflicts (decision version). An arrow from a class \({\mathcal {G}}_1\) to a class \({\mathcal {G}}_2\) means that every graph in \({\mathcal {G}}_1\) is also in \({\mathcal {G}}_2\). Label ‘PP’ means that for each fixed k the problem is solvable in pseudo-polynomial time in the given class, and label ‘sNPc’ means that for each fixed \(k\ge 2\) the problem is strongly NP-complete. Graph classes with results in the current paper are given in gray. All results from Chiarelli et al. (2023) are shown with round corners and no color. Results depicted in rectangles follow from the inclusion of graph classes. Note that for the case of \(\chi \)-bounded graph classes, we only claim strong NP-completeness for classes containing either the class of all bipartite graphs or the class of all line graphs of bipartite graphs

Full size image

1.2 Definitions and notation

For a positive integer k, we denote by [k] the set \(\{1,\ldots , k\}\). All graphs considered in this paper are finite, simple, and undirected. A vertex in a graph G is said to be isolated if it has no neighbors. An independent set in a graph G is a set of pairwise non-adjacent vertices. For a graph \(G = (V,E)\) and a set \(X\subseteq V\), we denote by G[X] the subgraph of G induced by X, that is, the graph with vertex set X in which two vertices are adjacent if and only if they are adjacent in G.

A bipartite graph \(G=(A\cup B, E)\) is convex if the vertices in A can be linearly ordered as \((a_1,\ldots , a_s)\) so that for every vertex \(b\in B\), the neighbors of b form a consecutive interval of vertices in A (see, e.g., Lipski and Preparata 1981). Such an ordering of A can be found in linear time using PQ-trees (Booth and Lueker 1976).

A bipartite graph is biconvex if both vertex sets A and B can be linearly ordered such that for every vertex \(a \in A\) (resp. \(b \in B\)) the neighbors of a (resp. neighbors of b) form a consecutive interval in B (resp. in A). Informally, a biconvex graph is convex on both sides.

2 Convex bipartite graphs

We will first derive our main result for the case when the conflict graph G is connected. Later, we will refer to Chiarelli et al. (2023, Lemma 13) to show that profit profiles determined during the execution of this algorithm for every connected component (as well as for isolated vertices) can be merged together for a solution on general graphs.

It will be useful to state the following observation for the solution of Fair k-Division of Indivisible Items, which can be seen as an instance of Fair k-Division Under Conflicts with an edgeless conflict graph G.

Given an instance \(I = (G,p_1,\ldots , p_k)\) of Fair k-Division Under Conflicts, a profit profile for I is a k-tuple \((q_1,\ldots , q_k)\in {\mathbb {Z}}_+^k\) such that there exists a partial k-coloring \((X_1,\ldots , X_k)\) of G for which \(q_j = p_j(X_j)\) for all \(j\in [k]\).

Lemma 1

For every \(k\ge 1\), the set of profit profiles for a given instance \((G,p_1,\ldots , p_k)\) of Fair k-Division Under Conflicts with edgeless conflict graph G can be computed in time \({\mathcal {O}}(n(Q+1)^k)\), where \(n = |V(G)|\) and \(Q = \max _{1\le j\le k}p_j(V(G))\).

Proof

Let \(V=\{v_1, \ldots , v_n\}\) and \(\Pi \) be the set of all profit profiles for the given instance. Observe that \(\Pi \) is initialized by the singleton consisting only of the all-zero profit profile. Then, we iterate over the vertices of G as follows. For every i from 1 to n, we consider every profit profile in \(\Pi \) and generate k new profit profiles from it by adding a profit of \(p_j(v_i)\) to the current entry at position j for every \(j\in [k]\). These \(k |\Pi |\) new profit profiles are added to the current set \(\Pi \) (trivially ignoring duplications). Altogether, there can be at most \({\mathcal {O}}((Q+1)^k)\) different profit profiles with \(Q = \max _{1\le j\le k}p_j(V)\). Thus, in each of the n iterations, at most \({\mathcal {O}}((Q+1)^k)\) profit profiles have to be considered to generate k (i.e., constantly many) candidates for the new profit profiles. \(\square \)

The main theorem of this section gives a pseudo-polynomial algorithm for connected convex graphs. Our algorithm is based on an approach similar to that of Díaz et al. (2021), relying on certain structural properties of convex bipartite graphs.

Theorem 2

For every \(k\ge 1\), Fair k-Division Under Conflicts is solvable in time \({\mathcal {O}}(n^{3k+1}(Q+1)^{2k})\) for connected n-vertex convex bipartite conflict graphs G, where \(Q=\max _{1\le j\le k}p_j(V(G))\).

Before proving Theorem 2, we introduce some notation. Let \(G = (A\cup B,E)\) be a connected convex bipartite graph, with vertices in A linearly ordered as \((a_1,\ldots , a_s)\) so that for every vertex \(b\in B\), the neighbors of b form a consecutive interval of vertices in A. Recall that such an ordering of A can be found in linear time using PQ-trees (Booth and Lueker 1976). Furthermore, we assume that G has at least two vertices. In particular, since G is connected, this implies that G does not have any isolated vertices, and sets A and B are both non-empty.

For each \(b\in B\), let \(b^-\) and \(b^+\) be the two elements of [s] such that \(N_G(b) = \{a_j\mid b^-\le j\le b^+\}\). Note that since G has no isolated vertices, \(b^-\) and \(b^+\) are well defined, but may coincide. We may also assume that vertices of B are sorted linearly as \((b_1,\ldots , b_t)\) so that for all \(1\le i<j\le t\), we have \(b_i^+\le b_j^+\), and if \(b_i^+= b_j^+\), then \(b_i^-\le b_j^-\). In other words, we consider vertices of B to be ordered non-decreasingly with respect to the larger endpoints of the intervals representing their neighborhoods, and in case of a tie, they are ordered non-decreasingly with respect to their smaller endpoints. See Fig. 2 for an example.

Fig. 2
figure 2

An example of a convex bipartite graph and the corresponding indices and sets as used in the proof

Full size image

First, we compute the set \(U\subseteq A\) of the larger endpoints of the neighborhoods of vertices in B, that is, \(U = \{a_{b^+}\mid b\in B\}\), and sort the elements of U increasingly by their index: \(U = \{a_{u_1}, \ldots , a_{u_r}\}\) such that \(u_1<\ldots < u_r\). (Note that \(u_r = s\) since G is connected.) For all \(j\in [r]\), we set:

$$\begin{aligned} A_j&= \{a_i\in A\mid 1\le i\le u_j\},\\ B_j&= \{b\in B\mid b^+\le u_j\},\,\text {and}\\ G_j&= G[A_j\cup B_j]. \end{aligned}$$

The graphs \(G_1,\ldots , G_r\) form an increasing sequence (with respect to the induced subgraph relation) of induced subgraphs of G such that \(G_r = G\). For each \(j\in [r]\), analogously to \(u_j\), we also define \(v_j\in [t]\) to be the index such that \(B_j = \{b_1, \ldots , b_{v_j}\}\). Note that \(v_1<\ldots <v_r\). We now point out some immediate but important facts regarding the above notions:

  1. (i)

    \(A_1\subsetneq \ldots \subsetneq A_r\), \(B_1\subsetneq \ldots \subsetneq B_r\).

  2. (ii)

    \(A_j{\setminus } A_{j-1} = \{a_{u_{j-1}+1},\ldots , a_{u_j}\}\) and \(B_j{\setminus } B_{j-1} = \{b_{v_{j-1}+1},\ldots , b_{v_j}\}\).

  3. (iii)

    For all \(i,i'\in \{u_{j-1}+1,\ldots , u_j\}\) with \(i<i'\), we have \(N_{G_j}(a_{i})\subseteq N_{G_j}(a_{i'})\subseteq B_j{\setminus } B_{j-1}\).

  4. (iv)

    For all \(i,i'\in \{v_{j-1}+1,\ldots , v_j\}\) with \(i<i'\), we have \(N_{G_j}(b_{i'})\subseteq N_{G_j}(b_i)\).

After these notational preparations, we proceed with the proof of Theorem 2.

Proof of Theorem 2

The proof of the theorem is constructive and relies on dynamic programming. Let us start with a high-level intuitive explanation: We develop a dynamic programming algorithm that considers a number of restricted subproblems on graphs \(G_j\) for increasing j. For each graph \(G_j\), \(j\in \{1,\dots ,r\}\) (as defined above) we guess (by enumerating all possibilities) the largest indexed vertex in \(V(G_j)\cap A = A_j\) for every color. This means that we go through all k-tuples \((i_1,\ldots , i_k)\in \{0,1,\ldots ,u_j\}^k\) and compute the set \(\Pi _j(i_1,\ldots , i_k)\), defined as the set of all profit profiles (see next paragraph for the definition) of \(G_j\) such that each agent \(\ell \in [k]\) is assigned vertex \(a_{i_\ell }\) and possibly other vertices from \(\{a_1, \ldots , a_{i_\ell -1}\} \cup B_j\). As the set of all profit profiles of partial k-colorings of G equals the union, over all \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_r\}^k\), of the sets \(\Pi _r(i_1,\ldots , i_k)\), this will give us a solution for our problem.

Definition of profit profiles \(\Pi _j (i_1,\dots ,i_k)\). For each \(j\in \{1,\dots ,r\}\) and each k-tuple \((i_1,\ldots , i_k)\in \{0,1,\dots ,u_j\}^k\), the set \(\Pi _j(i_1,\ldots , i_k)\) of profit profiles is defined to be the set of all k-tuples \((q_1,\ldots , q_k)\in {\mathbb {Z}}_+^k\) such that there exists a partial k-coloring \((X_1,\ldots , X_k)\) of \(G_j\) with the following property: for all \(\ell \in [k]\), we have \(q_\ell = p_\ell (X_\ell )\) and

$$\begin{aligned} i_\ell = \left\{ \begin{array}{ll} \max \{u \mid a_u\in X_\ell \}, &{} \hbox {if }X_\ell \cap A\ne \emptyset ; \\ 0, &{} \hbox {if }X_\ell \cap A = \emptyset . \end{array} \right. \end{aligned}$$
(1)

Note that for each \(\ell \in [k]\), the possible values of the \(\ell \)-th coordinate of any member of \(\Pi _j(i_1,\ldots , i_k)\) belong to the set \(\{0,1,\ldots , Q\}\) where \(Q = \max _{1\le j\le k}p_j(V(G))\). Thus, each set \(\Pi _j(i_1,\ldots , i_k)\) has at most \((Q+1)^k\) elements. Note also that for each fixed \(j\in [r]\), the total number of sets \(\Pi _j(i_1,\ldots , i_k)\) is of the order \({\mathcal {O}}(n^{k})\). The whole remainder of the proof deals with the explanation of how to compute the sets \(\Pi _j(i_1,\ldots , i_k)\) for each \(j\in [r]\) and each k-tuple \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_j\}^k\).

Computation of profit profiles for \(j=1\). In the initial case \(G_1\) is the subgraph of G induced by \(A_1\cup B_1\), where \(A_1 = \{a_1,\ldots , a_{u_1}\}\) and \(B_1 = \{b_1,\ldots , b_{v_1}\}\). Recall from properties (iii) and (iv) that \(N_{G_1}(a_{i})\subseteq N_{G_1}(a_{i'})\) for all \(i,i'\in [u_1]\) with \(i<i'\), and similarly \(N_{G_1}(b_{i'})\subseteq N_{G_1}(b_i)\) for all \(i,i'\in [v_1]\) with \(i<i'\). Consider a k-tuple \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_1\}^k\). We may assume that \(i_{\ell } = i_{\ell '}\) if and only if \(\ell = \ell '\) or \(i_{\ell } = i_{\ell '} = 0\), since vertex \(a_{i_\ell }\) can be assigned at most one color; in other words, for all k-tuples \((i_1,\ldots , i_k)\) not satisfying the above condition, we clearly have \(\Pi _1(i_1,\ldots , i_k) = \emptyset \). Note also that for each \(\ell \in [k]\) such that \(i_\ell > 0\), vertex \(a_{i_\ell }\) must be assigned to \(X_\ell \), the \(\ell \)-th color class, no vertex in \(A_1\) with index larger than \(i_\ell \) is assigned to \(X_\ell \), and, moreover, no vertex in \(B_1\) adjacent to \(a_{i_\ell }\) can be assigned to \(X_\ell \). To consider possible additional assignments of vertices to \(X_\ell \), we define \(I_\ell \) as the set containing vertices in \(B_1\) non-adjacent to \(a_{i_\ell }\) and vertices in \(A_1\) with index strictly smaller than \(i_\ell \).

Observation. \(I_\ell \) is an independent set in \(G_1\).

Proof

Suppose by contradiction that \(a_ib_{i'}\in E(G_1)\), with \(i<i_\ell \) and \(a_{i_\ell }b_{i'}\notin E(G_1)\). By construction of \(G_1\) we clearly have \(a_{u_1}b_{i'}\in E(G_1)\). But since \(i<{i_\ell }\le {u_1}\), this violates the assumption that the neighbors of \(b_{i'}\) form a consecutive interval of vertices in A. \(\square \)

Set \(Y_1 = \{a_{i_\ell }\mid 1\le \ell \le k \wedge i_\ell > 0\} \subseteq A_1\). Now notice that the remaining elements of \(X_\ell \) can be any of the vertices in \(I_\ell {\setminus } Y_1\). The reasoning is similar for all \(\ell \in [k]\) where \(i_\ell = 0\) since in this case no vertex in \(A_1\) is allowed to be assigned to \(X_\ell \), but any vertex in \(B_1\) can be. We, thus, define, for all \(\ell \in [k]\), a modified profit function \(p'_\ell \) on the vertices of \(G_1 {\setminus } Y_1\) which, informally speaking, assigns the original profits only to vertices in \(I_\ell \). Formally, we set for all \(v\in V(G_1 {\setminus } Y_1)\):

$$\begin{aligned} p'_\ell (v) = \left\{ \begin{array}{ll} 0, &{} \hbox {if }i_\ell =0 \hbox { and } v\in A_1;\\ 0, &{} \hbox {if }i_\ell >0 \hbox { and }v\in \{a_{i_\ell +1},\ldots , a_{u_1}\}\cup N_{G_1}(a_{i_\ell }); \\ p_\ell (v), &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

Note that for each \(\ell \), no two vertices of \(G_1{\setminus } Y_1\) with strictly positive value of the modified profit function \(p_\ell '\) are adjacent. Thus, to compute the set \(\Pi _1'\) of all possible profit profiles with respect to the modified profits \((p_1',\ldots , p_k')\) on the set \(V(G_1){\setminus } Y_1\), we can completely ignore the edges, and hence this set can be computed using Lemma 1. Adding the profit implied by index \(i_\ell \), we obtain

$$\begin{aligned} \Pi _1(i_1,\ldots , i_k) = \{(q_1,\ldots , q_k) \mid (q_1',\ldots , q_k') \in \Pi _1'\}, \end{aligned}$$

where

$$\begin{aligned} q_\ell = \left\{ \begin{array}{ll} q_\ell '+p_\ell (a_{i_\ell }), &{} \hbox {if }i_\ell >0; \\ q_\ell ', &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

This computation is carried out for each of the \({{\mathcal {O}}}(n^k)\) k-tuples \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_1\}^k\).

Computation of profit profiles for \(j>1\). After settling the case \(j=1\), we now consider \(j > 1\) and assume that all the relevant sets \(\Pi _{j-1}(i_1',\ldots , i_k')\) were already computed.

The main loop for a fixed value of j considers an arbitrary but fixed k-tuple \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_j\}^k\). Again, we may assume that \(i_{\ell } = i_{\ell '}\) if and only if \(\ell = \ell '\) or \(i_{\ell } = i_{\ell '} = 0\), since otherwise we again have \(\Pi _j(i_1,\ldots , i_k) = \emptyset \).

The main idea is a systematic structuring of the contributions from \(B_j{\setminus } B_{j-1}\). Therefore, we first guess the smallest indexed vertices in \(B_j{\setminus } B_{j-1}\) that will belong to each color class \(X_\ell \) (of course, this guess has to be performed for every k-tuple \((i_1,\ldots , i_k)\)). More formally, we consider all possible k-tuples \((m_1,\ldots , m_k)\in \{v_{j-1}+1,\ldots , v_j,\infty \}^k\), where \(\infty \) is a dummy symbol such that \(t<\infty \). To prevent assigning the same vertex to two agents, we restrict ourselves to the k-tuples \((m_1,\ldots , m_k)\) for which \(m_{\ell } = m_{\ell '}\) if and only if \(\ell = \ell '\) or \(m_{\ell } = m_{\ell '} = \infty \). We say that such a k-tuple \((m_1,\ldots , m_k)\) is compatible with the current k-tuple \((i_1,\ldots , i_k)\) from the A-side if for all \(\ell \in [k]\) such that \(i_\ell >0\) and \(m_\ell <\infty \), vertices \(a_{i_\ell }\) and \(b_{m_\ell }\) are non-adjacent in \(G_j\) (or, equivalently, in G). We denote by \({\mathcal {M}}_j = {\mathcal {M}}_j(i_1,\ldots , i_k)\) the set of all such k-tuples \((m_1,\ldots , m_k)\) compatible with the current guess \((i_1,\ldots , i_k)\). For simplicity of notation, in the rest of the proof, we do not explicitly write the dependency on the current guess \((i_1,\ldots , i_k)\).

Next, we define the following set:

$$\begin{aligned} Y_j&= \{a_{i_\ell }\mid 1\le \ell \le k \wedge i_\ell > 0\}{\setminus } A_{j-1}, \end{aligned}$$

and, for each k-tuple \((m_1,\ldots , m_k)\in {\mathcal {M}}_j\), a set \(Z_j\) (analogous to \(Y_j\) on the B-side) and with it the resulting graph \(G_j'\) representing vertices added in the current iteration j and still open for assignment:

$$\begin{aligned} Z_j&= \{b_{m_\ell }\mid 1\le \ell \le k \wedge m_\ell <\infty \}\,, \\ G_j'&= G[(A_{j}{\setminus } (A_{j-1}\cup Y_j))\cup (B_j{\setminus } (B_{j-1}\cup Z_j)]\,. \end{aligned}$$

We define, for all \(\ell \in [k]\), a modified profit function \(p'_\ell \) on the vertices of \(G_j'\) which assigns the original profits to those vertices that still might be assigned to color \(\ell \) without violating the definitions of \(i_\ell \) and \(m_\ell \). We set for all \(v\in V(G_j')\):

$$\begin{aligned} p'_{\ell }(v)= {\left\{ \begin{array}{ll} 0, &{} \text {if }v\in \left\{ a_{\max \{i_{\ell },u_{j-1}\}+1},\ldots ,a_{u_{j}}\right\} ;\\ 0, &{} \text {if }i_\ell >0 \text { and } v\in N_{G_j}(a_{i_\ell });\\ 0, &{} \text {if }v\in \left\{ b_{v_{j-1}+1},\ldots ,b_{\min \{m_{\ell },v_{j}+1\}-1}\right\} ;\\ 0, &{} \text {if }m_\ell <\infty \text { and } v\in N_{G_j}(b_{m_\ell });\\ p_{\ell }(v), &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Also here, similarly to the case \(j = 1\), we will need an independence property of the graph \(G_j'\) that can be derived from the convexity of G.

Observation. For each \(\ell \), no two vertices of \(G_j'\) with strictly positive value of the modified profit function \(p_\ell '\) are adjacent.

Proof

Suppose by contradiction that \(a_ib_{i'}\in E(G_j')\) where \(p_\ell (a_i)>0\) and \(p_\ell (b_{i'})>0\). Then, \(i<i_\ell \) and \(i'>m_\ell \). Since the k-tuple \((m_1,\ldots , m_k)\) is compatible with \((i_1,\ldots , i_k)\), vertices \(a_{i_\ell }\) and \(b_{m_\ell }\) are non-adjacent in \(G_j\). Furthermore, by construction of \(G_j\) vertices \(a_{u_j}\) and \(b_{i'}\) are adjacent in \(G_j\) (and in G). Now, as vertex \(b_{i'}\) is adjacent in G to both \(a_i\) and \(a_{u_j}\), the inequalities \(i<{i_\ell }\le {u_j}\) and the convexity property imply that \(b_{i'}\) is adjacent in G (and thus in \(G_j\)) to \(a_{i_\ell }\). Finally, applying property (iv) to \(m_\ell <i'\), we obtain that \(N_{G_j}(b_{i'})\subseteq N_{G_j}(b_{m_\ell })\), which contradicts the fact that \(a_{i_\ell }\) is adjacent in \(G_j\) to \(b_{i'}\) but not to \(b_{m_\ell }\). \(\square \)

Now, we determine the set \(\Pi _j'(m_1,\ldots , m_k)\) of all possible profit profiles on the set \(V(G_j')\) with respect to the modified profits \((p_1',\ldots , p_k')\). In the computation of \(\Pi _j'(m_1,\ldots , m_k)\), we can again completely ignore the edges, and hence, also this set can be computed as described in Lemma 1.

Combining profit profiles after each increment of j. To complete the construction of \(\Pi _{j}(i_{1},\dots ,i_{k})\), it remains to combine these profit profiles for \(G_j'\) with the profits implied by the choice of the two k-tuples on the A- and B-side (in sets \(A_j{\setminus } A_{j-1}\) and \(B_j{\setminus } B_{j-1}\), respectively) and with those computed recursively on the graph \(G_{j-1}\). Note that there are no edges in \(G_j\) joining a vertex in \(A_j{\setminus } A_{j-1}\) with a vertex in \(B_{j-1}\). Moreover, for every k-tuple \((m_1,\ldots , m_k)\in {\mathcal {M}}_j\), we already know both the largest vertex in \(A_j\) (if any) and the smallest vertex in \(B_j{\setminus } B_{j-1}\) (if any) that belongs to each \(X_\ell \).

Let \({\mathcal {I}}_j = {\mathcal {I}}_j(i_1,\ldots , i_k)\) be the set of all k-tuples \((i_1',\ldots , i_k')\in \{0,1,\ldots , u_{j-1}\}^k\) for which \(i_\ell ' = i_\ell \) for all \(\ell \in [k]\) such that \(i_\ell \le u_{j-1}\). The intuition behind the definition of the set \({\mathcal {I}}_j\) is as follows. The corresponding k-tuples encode the choices for \(i_\ell \) that were available already in the previous iteration for \(j-1\) and, therefore, for each \((i_1',\ldots , i_k')\in {\mathcal {I}}_j\), the set \(\Pi _{j-1}(i_1',\ldots , i_k')\) has already been computed. More precisely, consider a partial coloring \((X_1,\ldots , X_k)\) of \(G_j\) such that \(i_\ell = \max \{u\mid a_u\in X_\ell \}\) if \(X_\ell \cap A \ne \emptyset \) and \(i_\ell = 0\) if \(X_\ell \cap A = \emptyset \). We consider three cases depending on the value of \(i_\ell \):

  • If \(i_\ell = 0\), then no vertex from \(A_j\) is assigned to agent \(\ell \) and thus the same condition will hold for the restriction of \(X_\ell \) to \(G_{j-1}\); thus we impose the condition \(i_\ell ' = 0 = i_\ell \) in this case.

  • If \(0 < i_\ell \le u_{j-1}\), then we again want to require that \(i_\ell ' = i_\ell \) since in this case vertex \(a_{i_\ell }\) will be the largest indexed vertex assigned to agent \(\ell \) not only in \(A_j\) but also in \(A_{j-1}\).

  • Finally, if \(i_\ell > u_{j-1}\), then the largest indexed vertex assigned to agent \(\ell \) belongs to \(A_j{\setminus } A_{j-1}\), which imposes no constraints on the largest indexed vertex assigned to agent \(\ell \) from the set \(A_{j-1}\).

The profit contribution added in the current iteration j directly by the choice of \((i_{1},\dots ,i_{k})\) will be denoted by the k-tuple \(q^A\). Similarly, for every choice of \(\mu =(m_1,\ldots , m_k)\in {\mathcal {M}}_j\) the resulting profit profile is denoted by the k-tuple \(q^B(\mu )\). Formally, we have the following:

$$\begin{aligned} q^A&=(q_1^A,\dots ,q_k^A),\text { where } q_\ell ^A = \left\{ \begin{array}{ll} p_\ell (a_{i_\ell }), &{} \hbox {if }i_\ell \ge u_{j-1}+1; \\ 0, &{} \hbox {otherwise;} \end{array} \right. \\ q^B(\mu )&=(q_1^B,\dots ,q_k^B),\text { where } q_\ell ^B = \left\{ \begin{array}{ll} p_\ell (b_{m_\ell }), &{} \hbox {if }m_\ell < \infty ; \\ 0, &{} \hbox {otherwise.} \end{array} \right. \end{aligned}$$

Now, we are ready to paste together all parts contributing to the set of profit profiles \(\Pi _{j}(i_{1},\dots ,i_{k})\) in iteration j for the current guess \((i_{1},\dots ,i_{k})\). Namely, we take the union over all guesses from the preceding iteration \(j-1\) which are compatible with \((i_{1},\dots ,i_{k})\), i.e. the union over all k-tuples \(\tau =(i_1',\ldots , i_k')\in {\mathcal {I}}_j\). Recall that any such \(\tau \) coincides with the current guess for all indices \(i_\ell \le u_{j-1}\). From the previous iteration, we have at hand a set of potential profit profiles \(\Pi _{j-1}(\tau )\) for each such \(\tau \). Moreover, we also take the union over all possible choices \(\mu \in {\mathcal {M}}_j\), which are compatible with the current guess \((i_{1},\dots ,i_{k})\) by definition of \({\mathcal {M}}_j\). The possible contributions from the newly considered vertices \(V(G_j{\setminus } G_{j-1})\) in compliance with \((i_{1},\dots ,i_{k})\) and \(\mu \) are added through \(\Pi '_{j}(\mu )\). Altogether this yields:

$$\begin{aligned} \Pi _{j}(i_{1},\dots ,i_{k})=\bigcup _{\begin{array}{c} {\scriptstyle \tau \in {\mathcal {I}}_{j},}\\ {\scriptstyle \mu \in {\mathcal {M}}_{j}} \end{array}}\bigcup _{\begin{array}{c} {\scriptstyle q\in \Pi _{j-1}(\tau ),}\\ {\scriptstyle q'\in \Pi '_{j}(\mu )} \end{array}}\left\{ q+q'+q^{A}+q^{B}(\mu )\right\} . \end{aligned}$$
(2)

Recall that, as the set of all profit profiles of partial k-colorings of G equals the union, over all \((i_1,\ldots , i_k)\in \{0,1,\ldots , u_r\}^k\), of the sets \(\Pi _r(i_1,\ldots , i_k)\), assuming the correctness of Eq. (2), this gives the solution of Fair k-Division Under Conflicts and concludes the proof.

Correctness of Eq. (2). First, consider a profit profile in \(\Pi _j(i_1,\ldots , i_k)\). To see that the profile can be written as the sum \(q+q'+q^A+q^B(\mu )\) for some \(q\in \Pi _{j-1}(\tau )\) with \(\tau \in {\mathcal {I}}_j\) and \(q'\in \Pi '_j(\mu )\) with \(\mu \in {\mathcal {M}}_j\), fix any partial k-coloring \((X_1,\ldots , X_k)\) of \(G_j\) “compatible with” \((i_1,\ldots , i_k)\) and having the given profit profile. For each color \(\ell \in [k]\), we determine the vertex in \(X_\ell \cap (B_j{\setminus } B_{j-1})\) (if any) with the smallest index. Such vertices define a k-tuple \(\mu \in {\mathcal {M}}_j\) and define a set \(Z_j\) that corresponds to a profit profile \(q^B(\mu )\). Similarly, the set of all vertices in \(X_\ell \cap (A_j{\setminus } A_{j-1})\) with the largest index (if any), over all \(\ell \in [k]\), define a set \(Y_j\) that corresponds to a profit profile \(q^A\). Vertices in \(X_\ell \cap ((A_j\cup B_j){\setminus } (Y_j\cup Z_j))\) correspond to an independent set in \(G_j' = G[(A_{j}{\setminus } (A_{j-1}\cup Y_j))\cup (B_j{\setminus } (B_{j-1}\cup Z_j)]\), and all these independent sets form a partial k-coloring of \(G_j'\) with profit profile \(q'\in \Pi '_j(\mu )\). Finally, vertices in \(X_\ell \cap V(G_{j-1})\) form an independent set in \(G_{j-1}\), and all these independent sets form a partial k-coloring of \(G_{j-1}\) with profit profile \(q\in \Pi _{j-1}(\tau )\). By construction, the profit profile of \((X_1,\ldots , X_k)\) is precisely the sum \(q+q'+q^A+q^B(\mu )\).

Conversely, consider some \(q\in \Pi _{j-1}(\tau )\) with \(\tau \in {\mathcal {I}}_j\) and \(q'\in \Pi '_j(\mu )\) with \(\mu = (m_1,\ldots , m_k)\in {\mathcal {M}}_j\). Fix any partial k-coloring \((X_1,\ldots , X_k)\) of \(G_{j-1}\) “compatible with” \(\tau =(i_1',\ldots , i_k')\) having profit profile q and set, as before, \(Y_j = \{a_{i_\ell }\mid 1\le \ell \le k \wedge i_\ell > 0\}{\setminus } A_{j-1}\), \(Z_j = \{b_{m_\ell }\mid 1\le \ell \le k \wedge m_\ell <\infty \}\), and \(G_j' = G[(A_{j}{\setminus } (A_{j-1}\cup Y_j))\cup (B_j{\setminus } (B_{j-1}\cup Z_j)]\). Fix any partial k-coloring \((X_1',\ldots , X_k')\) of \(G_{j}'\) having a \(p'\)-profit profile equal to the profile \(q'\in \Pi '_j(\mu )\) we considered at the beginning. Furthermore, for all \(\ell \in [k]\) and all \(v\in X'_\ell \), we may assume that \(p'(v)>0\) (otherwise we can simply remove v from \(X'_\ell \)). For each \(\ell \in [k]\), let us denote by \(Y^\ell \) the set \(\{a_{i_\ell }\}\) if \(i_\ell \in \{u_{j-1}+1\ldots , u_j\}\), and \(Y^\ell = \emptyset \), otherwise. For the considered \(\mu \), we denote by \(Z^\ell \) the set \(\{b_{m_\ell }\}\) if \(m_\ell <\infty \), and \(Z^\ell = \emptyset \), otherwise. It now suffices to show that for each \(\ell \in [k]\), the set \(X_\ell \cup X_\ell '\cup Y^\ell \cup Z^\ell \) is independent in G. By construction, each of the sets \(X_\ell \), \(X_\ell '\), \(Y^\ell \), and \(Z^\ell \) is independent. We justify that there are no edges between any two of these sets as follows.

  • There are no edges in G between \(B_{j-1}\) and \(A_j{\setminus } A_{j-1}\), hence there are no edges between \(X_\ell \cap B\) and \(Y^\ell \cup (X_\ell '\cap A_j)\).

  • There are no edges between \(X_{\ell }\cap A\) and \(Z^{\ell }\).

    Suppose for a contradiction that \(m_\ell <\infty \) and \(b_{m_\ell }\) is adjacent to a vertex \(a\in X_{\ell }\cap A\). Then \(a = a_g\) for some \(g\in [u_{j-1}]\) and, in particular, \(i_{\ell }\ge i_{\ell }'\ge g\) and this \(i_\ell >0\). Note also that \(b_{m_\ell }\) is non-adjacent to \(a_{i_\ell }\), since \(\mu = (m_1,\ldots , m_k)\) is compatible with \((i_1,\ldots , i_k)\). Thus, \(b_{m_\ell }\) is adjacent to \(a_g\), non-adjacent to \(a_{i_\ell }\), and adjacent to \(a_{u_j}\). Since \(g\le i_\ell \le j\), we obtain a contradiction with the convexity of G.

  • There are no edges between \(X_{\ell }\cap A\) and \(X_\ell '\cap B\).

    Suppose for a contradiction that there exists a pair of adjacent vertices \(a\in X_{\ell }\cap A\) and \(b\in X_\ell '\cap B\). Then \(a = a_g\) for some \(g\le [u_{j-1}]\) and \(b = b_h\) for some \(h\in \{v_{j-1}+1,\ldots , v_j\}\). Again, we have \(i_{\ell }\ge i_{\ell }'\ge g\) and thus \(i_\ell >0\). Since \(b_h\in X_\ell '\), we have \(p'(b_h)>0\) and thus \(b_h\) is not adjacent to \(a_{i_\ell }\). Thus, \(b_{h}\) is adjacent to \(a_g\), non-adjacent to \(a_{i_\ell }\), and adjacent to \(a_{u_j}\). Since \(g\le i_\ell \le j\), we obtain a contradiction with the convexity of G.

  • There are no edges between \(X_{\ell }'\cap A\) and \(Z^{\ell }\).

    This is true since if \(m_\ell <\infty \), then all vertices \(v\in X_{\ell }'\cap A\) satisfy \(p'(v)>0\) and are thus non-adjacent to \(b_{m_\ell }\) by the definition of the modified profit function.

  • Similarly, there are no edges between \(X_{\ell }'\cap B\) and \(Y^{\ell }\).

  • Finally, there are no edges between \(Y^\ell \) and \(Z^\ell \), since \(\mu = (m_1,\ldots , m_k)\) is compatible with \((i_1,\ldots , i_k)\).

We conclude that Eq. (2) is correct.

Time complexity analysis. Concerning the running time, we restrict ourselves to a rough estimate. The ordering of sets A and B, along with the computation of set U and indices \(u_1,\ldots , u_r\) and \(v_1,\ldots , v_r\) can be done in time \({\mathcal {O}}(|V(G)|+|E(G)|+|V(G)|\log |V(G)|)\), i.e., \({\mathcal {O}}(n^2)\). Then, in each of the \({\mathcal {O}}(n)\) iterations over j we iterate over each of the \({\mathcal {O}}(n^k)\) k-tuples \((i_{1},\dots ,i_{k})\in \{0,1,\ldots , u_j\}^k\), and determine the set \({\mathcal {M}}_{j}\) of \({\mathcal {O}}(n^k)\) compatible k-tuples in \({\mathcal {O}}(n^k)\) time. (We first compute, in time \({\mathcal {O}}(kn)\), the index sets of non-neighbors in \(B_j{\setminus } B_{j-1}\) of each vertex \(a_{i_\ell }\) (whenever \(i_\ell >0\)) and then take the Cartesian product of these sets, each augmented by \(\infty \).) For every \(\mu \in {\mathcal {M}}_{j}\), there are \({\mathcal {O}}((Q+1)^k)\) profit profiles in \(\Pi '_{j}(\mu )\) which can be computed in \({{\mathcal {O}}}(n(Q+1)^k)\) time according to Lemma 1.

The final combination of entries in (2) goes over all \(\tau \in {\mathcal {I}}_{j}\), where \(|{\mathcal {I}}_{j}|\) is in \({\mathcal {O}}(n^k)\), and for every \(\tau \) there are \({\mathcal {O}}((Q+1)^k)\) profit profiles in \(\Pi _{j-1}(\tau )\). Each of them is combined with each of \({\mathcal {O}}((Q+1)^k)\) profit profiles in \(\Pi '_{j}(\mu )\) for all \({\mathcal {O}}(n^k)\) choices of \(\mu \). Thus, there are \({\mathcal {O}}(n^{2k}(Q+1)^{2k})\) candidates to be considered in (2) for inclusion in \(\Pi _{j}(i_{1},\dots ,i_{k})\).

This yields an overall running time of \({\mathcal {O}}(n^{3k+1}(Q+1)^{2k})\). \(\square \)

If G is not connected, then we compute for every component the set of all profit profiles for Fair k-Division Under Conflicts as described above and then aggregate these outputs.

Summarizing, we obtain the following generalization of Theorem 2.

Corollary 3

For every \(k\ge 1\), Fair k-Division Under Conflicts is solvable in time \({\mathcal {O}}(n^{3k+1}(Q+1)^{2k})\) for n-vertex convex bipartite conflict graphs G, where \(Q = \max _{1\le j\le k}p_j(V(G))\).

Proof

Let G consist of c connected components \(G_i\), \(i=1,\ldots ,c\), with \(|V(G_i)|=n_i\) and \(\sum _{i=1}^c n_i=n\). The running time is composed of two parts. At first, the profit profile is computed for each of the c components. The asymptotic running time can be bounded by

$$\begin{aligned} \sum _{i=1}^c n_i^{3k+1}(Q+1)^{2k} \le \left( \sum _{i=1}^c n_i\right) ^{3k+1}\!\!(Q+1)^{2k} =n^{3k+1}(Q+1)^{2k}. \end{aligned}$$

Second, the c profit profiles each of size \({\mathcal {O}}((Q+1)^{k})\) have to be merged. We start with the profit profiles determined for the first component and merge the profit profiles from the second component by considering every pair of profiles from first and second component and performing a vector addition to obtain a new profit profile. Continuing this process, in every iteration, the profit profiles of the next component are merged with the previously existing profiles. Throughout this process, the total number of profit profiles remains pseudo-polynomially bounded. Finally, the best objective function value is determined by evaluating all profit profiles. A more formal description of this approach was given in Lemma 13 of Chiarelli et al. (2023). Altogether, this second part requires \({\mathcal {O}}((c-1)(Q+1)^{2k})\) time, which is dominated by the effort of the first part. \(\square \)

3 Graphs of bounded clique-width

In this section, we present a pseudo-polynomial time dynamic programming algorithm for Fair k-Division Under Conflicts for conflict graphs of bounded clique-width. This is an improvement over the previous result for graphs of bounded treewidth, which was so far the only positive result for non-perfect graphs.

Clique-width, introduced 1993 in Courcelle et al. (1993), is a parameter defined by a construction process where only a limited number of vertex labels are available. Vertices with the same label at some point must be treated uniformly in subsequent steps (see below). The clique-width \(\text {cw}(G)\) of a graph G is the minimum number of labels that suffice to construct G in this way. NP-completeness and inapproximability of the clique-width of a graph were shown in Fellows et al. (2009). For graphs of bounded clique-width many hard optimization problems admit polynomial-time algorithms, see, e.g., Courcelle et al. 2000; Espelage et al. 2001; Gerber and Kobler 2003; Rao 2007.

Relations between treewidth and clique-width were elaborated in Courcelle and Olariu (2000). In particular, bounded treewidth \(\text {tw}(G)\) of a graph G implies bounded clique-width since \(\text {cw}(G) \le 3\cdot 2^{\text {tw}(G)}-1\) as shown by Corneil and Rotics (2005). However, the opposite implication is not true as can be seen from the family of complete graphs which have clique-width 2 but treewidth \(|V|-1\).

Another parameter of a graph G related to treewidth is rank-width \(\text {rw}(G)\) introduced in Oum and Seymour (2006). Rank-width is also derived from a hierarchical decomposition of the graph. Informally speaking, treewidth measures the width of a separation into two sides, whereas rank-width measures the rank of the adjacency matrix of the edges between the two sides of the separation. Without going into more details, let us just mention that it was shown in Oum and Seymour (2006) that \(\text {rw}(G) \le \text {cw}(G) \le 2^{\text {rw}(G)+1}-1\). Therefore, bounded clique-width is equivalent to bounded rank-width.

In the following, we will describe the labeling process of the graph decomposition associated to clique-width in more detail.

A labeled graph is a graph in which every vertex is assigned some label from \({\mathbb {N}}\). If all vertex labels belong to the set [k], then we say that the graph is k-labeled. The clique-width of a graph G is defined as the smallest positive integer k such that a k-labeled graph isomorphic to G can be constructed with the following operations:

  • i(v): creating a new one-vertex graph with vertex v labeled i,

  • \(G\oplus H\): disjoint union of two already constructed labeled graphs G and H,

  • \(\eta _{i,j}\), for \(i\ne j\): adding to G all edges between vertices labeled i and vertices labeled j,

  • \(\rho _{i\rightarrow j}\), for \(i\ne j\): relabeling every vertex labeled i with label j.

A construction of a graph G with the above four operations can be represented by an algebraic expression, which is called a k-expression if it uses at most k labels. Given a k-expression \(\sigma \), we denote by \(|\sigma |\) its encoding length. A graph class \({\mathcal {G}}\) is said to be of bounded clique-width if there exists a nonnegative integer k such that each graph in \({\mathcal {G}}\) has clique-width at most k.

Polynomial-time algorithms for graphs with bounded clique-width are typically developed using dynamic programming based on a k-expression building the input graph. If a k-expression is not available, then one can use any of the available algorithms in the literature for computing an expression with at most f(k) labels for some exponential function f (see Fomin and Korhonen 2022; Jeong et al. 2021; Oum 2009; Oum and Seymour 2006). The currently fastest such algorithm is due to Fomin and Korhonen (2022); for an integer k and an n-vertex graph G, it runs in time \(2^{2^{O(k)}}n^2\) and either computes a \((2^{2k+1}-1)\)-expression of G or correctly determines that the clique-width of G is more than k.

We can now proceed to prove the following theorem.

Theorem 4

For every two positive integers k and \(\ell \), Fair k-Division Under Conflicts is solvable in time \({{\mathcal {O}}}\left( 4^{k\ell }|\sigma |(Q+1)^{2k}\right) \), if the conflict graph G has clique-width at most \(\ell \) and is given by an \(\ell \)-expression \(\sigma \), where \(Q = \max _{1\le j\le k}p_j(V(G))\).

Proof

We extend the standard dynamic programming algorithm for graphs of bounded clique-width for the case \(k = 1\), that is, the maximum weight independent set problem (see, e.g., Gurski 2008). Given a partial k-coloring \(c = (X_1,\ldots , X_k)\) of an \(\ell \)-labeled graph H, the label profile of c (with respect to H) is the k-tuple \((L_1,\ldots , L_k)\) where \(L_j\) is the set of labels in \([\ell ]\) appearing on some vertex of \(X_j\), for all \(j \in [k]\). For each labeled subgraph H of G that appears in the process of constructing G using \(\sigma \) and each k label sets \(L_1,\ldots , L_k\subseteq [\ell ]\), we compute the set \(P(H,L_1,\ldots , L_k)\) of all profit profiles \((q_1,\ldots , q_k)\) of partial k-colorings c of H such that the label profile of c equals \((L_1,\ldots , L_k)\). We then have four cases depending on the type of H. In each case, we derive a formula of how to compute the set \(P(H,L_1,\ldots , L_k)\) from the previously computed sets of this type.

  1. 1.

    H is a one-vertex graph consisting of a vertex v labeled i.

    There are only \(k+1\) partial k-colorings of H: the trivial partial k-coloring \(\emptyset ^k\) consisting of k empty sets, and, for each \(j\in [k]\), the partial k-coloring \(c_j = (X_1,\ldots , X_k)\) where \(X_j = \{v\}\) and \(X_{j'} = \emptyset \) for all \(j'\in [k]{\setminus }\{j\}\).

    The label profile of \(\emptyset ^k\) is \(\emptyset ^k\). For each \(j\in [k]\), the label profile of \(c_j\) is the k-tuple \((L_1,\ldots , L_k)\) where \(L_j=\{i\}\) and \(L_{j'}=\emptyset \) for all \(j'\ne j\). Thus, denoting by \({{\textbf {e}}}_j(p_j(v))\) the k-tuple in \({\mathbb {Z}}_+^k\) with j-th coordinate equal to \(p_j(v)\) and all the other coordinates equal to 0, we have the following formula:

    $$\begin{aligned} P(H,L_1,\ldots , L_k)=\left\{ \begin{array}{ll} \{{{\textbf {e}}}_j(p_j(v))\},&{} \text {if }L_j=\{i\} \text { and } L_{j'}=\emptyset \text { for all }{j'}\ne j,\\ \{(0,\dots , 0)\}, &{} \text {if }L_j=\emptyset \text { for all }{j}\in [k],\\ \emptyset ,&{} \textrm{otherwise}. \end{array} \right. \end{aligned}$$

    While in the remaining three cases, the assumptions on H are different, we always describe how to compute the set \(P(H,L_1,\ldots , L_k)\) for an arbitrary but fixed collection of k label sets \(L_1,\ldots , L_k\subseteq [\ell ]\).

  2. 2.

    H is the disjoint union of two labeled graphs \(H_1\) and \(H_2\).

    Let \(c=(X_1,\ldots , X_k)\) be a partial k-coloring of H with label profile \((L_1,\ldots , L_k)\). Then for \(i\in \{1,2\}\), we have that \(c_i=(X_1\cap V(H_i),\ldots , X_k\cap V(H_i))\) is a partial k-coloring of \(H_i\). Let us denote by \((L_1',\dots , L_k')\) and \((L_1'',\dots , L_k'')\) the label profiles of \(c_1\) and \(c_2\), respectively. Then, \(L_j = L_j'\cup L_j''\) for all \(j\in [k]\). Furthermore, the converse direction holds as well: for any two partial k-colorings \(c_1=(X_1',\ldots , X_k')\) and \(c_2=(X_1'',\ldots , X_k'')\) of \(H_1\) and \(H_2\), respectively, the k-tuple \(c=(X_1'\cup X_1'', \dots , X_k'\cup X_k'') \) is a partial k-coloring of H with label profile \((L_1'\cup L_1'',\dots , L_k'\cup L_k'')\), where \((L_1',\dots , L_k')\) and \((L_1'',\dots , L_k'')\) are the label profiles of \(c_1\) and \(c_2\), respectively. This bijective correspondence yields the following formula:

    $$\begin{aligned} P(H,L_1,\ldots , L_k)=\bigcup _{}\{\mathbf {q_1}+\mathbf {q_2}\mid \mathbf {q_1}\in P(H_1,L_1',\dots , L_k'), \mathbf {q_2}\in P(H_2,L_1'', \dots , L_k'')\}, \end{aligned}$$

    where the union is taken over all collections \((L_1',\dots , L_k')\) and \((L_1'',\dots , L_k'')\) of label sets such that \(L_j'\cup L_j''=L_j\) for all \(j\in [k]\).

  3. 3.

    H is obtained from a labeled graph \(H'\) by adding all edges between vertices labeled i and vertices labeled j where \(i \ne j\).

    Assume first that there exists some \(s\in [k]\) such that \(\{i,j\}\subseteq L_s\) and let \(c=(X_1,\dots , X_k)\) be a partial k-coloring of H with label profile \((L_1,\dots , L_k)\). Since \(\{i,j\}\subseteq L_s\), there are vertices \(v_1\) and \(v_2\) of H labeled i and j, respectively, such that \(\{v_1,v_2\}\subseteq X_s\). By the assumption on H all vertices labeled i are adjacent in H to all vertices labeled j, so it is not possible that \(\{v_1,v_2\}\subseteq X_s\), since \(X_s\) is an independent set in H; a contradiction. It follows that there is no partial k-coloring of H with label profile \((L_1,\dots , L_k)\), so in this case \(P(H,L_1,\ldots , L_k)=\emptyset .\)

    Assume now that for every \(s\in [k]\) we have that \(|L_s\cap \{i,j\}|\le 1\). In this case, every partial k-coloring of H with label profile \((L_1,\dots , L_k)\) is also a partial k-coloring of \(H'\) with the same label profile (with respect to \(H'\)), and vice versa. It follows that \(P(H,L_1,\ldots , L_k)=P(H', L_1,\dots , L_k)\). Altogether, we have the following equality:

    $$\begin{aligned} P(H,L_1,\ldots , L_k)=\left\{ \begin{array}{ll} P(H', L_1,\dots , L_k),&{} \hbox {if }|\{i,j\}\cap L_s|\le 1 \text { for all } s\in [k],\\ \emptyset ,&{} \textrm{otherwise}. \end{array} \right. \end{aligned}$$
  4. 4.

    H is obtained from a labeled graph \(H'\) by relabeling all vertices labeled i to vertices labeled j.

    Let \(c=(X_1,\dots , X_k)\) be a partial k-coloring of H with label profile \((L_1,\dots , L_k)\). Observe that it follows from the assumption on H that no vertex in H has label i.

    If there exists some \(s\in [k]\) such that \(i\in L_s\), then there is a vertex \(v\in X_s\) labeled i; a contradiction. It follows that there is no partial k-coloring of H with label profile \((L_1,\dots , L_k)\), and we have that \(P(H, L_1,\dots , L_k)=\emptyset \) in this case.

    Assume now that for all \(s\in [k]\) we have that \(i\notin L_s\). Let \(I=\{s\in [k]\mid j\in L_s\}\) and consider an arbitrary \(s\in I\). The vertices in \(X_s\) form an independent set in H and, thus, also in \(H'\). Since \(j\in I\), the set \(L_s\) contains j and, therefore, there exists a vertex \(v\in X_s\) such that the label of v in H is j. Thus, the set \(X_{sj}\) of all vertices in \(X_s\) labeled j in H is non-empty. Furthermore, since the label in \(H'\) of any vertex in \(X_{sj}\) is either i or j, the label set of \(X_s\) in \(H'\) depends on whether there exists a vertex in \(X_{sj}\) labeled i in \(H'\) and whether there exists a vertex in \(X_{sj}\) labeled j in \(H'\). More precisely, the dependency is as follows.

    • If there exists a vertex in \(X_{sj}\) labeled i in \(H'\) as well as one labeled j in \(H'\), then the label set of \(X_s\) in \(H'\) is \(L_s\cup \{i\}\) (recall that \(j\in L_s\)).

    • If all vertices in \(X_{sj}\) are labeled i in \(H'\), then the label set of \(X_s\) in \(H'\) is \((L_s{\setminus } \{j\})\cup \{i\}\).

    • If all vertices in \(X_{sj}\) are labeled j in \(H'\), then the label set of \(X_s\) in \(H'\) is \(L_s\).

    We conclude that the vertices of \(X_s\) form in \(H'\) an independent set with label set being equal either to \(L_s\), to \((L_s{\setminus } \{j\})\cup \{i\}\), or to \(L_s\cup \{i\}\). Therefore, c is a partial coloring of \(H'\) with label profile \((L_1',\dots , L_k')\) such that for all \(s\in I\) we have \(L_s'\in \{L_s, (L_s{\setminus } \{j\})\cup \{i\}, L_s\cup \{i\}\}\), and for all \(s\in [k]{\setminus } I\) we have \(L_s'=L_s\). Conversely, for any k label sets \(L_1',\dots , L_k'\subseteq [\ell ]\) such that \(L_s'\in \{L_s, (L_s{\setminus } \{j\})\cup \{i\}, L_s\cup \{i\}\}\) for all \(s\in I\) and \(L_s'=L_s\) for all \(s\in [k]{\setminus } I\), any partial coloring of \(H'\) with label profile \((L_1',\dots , L_k')\) is a partial coloring of H with label profile \((L_1,\ldots , L_k)\).

    Altogether, we thus obtain the following equality:

    $$\begin{aligned} P(H,L_1,\ldots , L_k)= \left\{ \begin{array}{ll} \emptyset , &{} \hbox {if } i\in L_s \hbox { for some } s\in [k] \\ \bigcup P(H', L_1',\dots , L_k'), &{} \hbox {otherwise}, \end{array} \right. \end{aligned}$$

    where the union in the second case is taken over all k-tuples of label sets \(L_1',\dots , L_k'\subseteq [\ell ]\) such that for all \(s\in I\) we have \(L_s'\in \{L_s, (L_s{\setminus } \{j\})\cup \{i\}, L_s\cup \{i\}\}\), and for all \(s\in [k]{\setminus } I\) we have \(L_s'=L_s\).

Time complexity analysis. From the \(\ell \)-expression \(\sigma \), we compute in time \(|\sigma |\) a rooted tree T describing the construction of G. Each node of T corresponds to a labeled subgraph H of G. For each such subgraph H, we consider all the \(2^{\ell k}\) different collections of k label sets \((L_1,\dots , L_k)\), obtained by choosing a subset of \([\ell ]\) for each coordinate. We explain the time complexity separately for Case 2. For Case 2, we can initialize all the sets \(P(H,L_1, \dots , L_k)\) to be empty and iterate over all \(4^{k\ell }\) pairs of collections \((L_1',\dots , L_k')\) and \((L_1'',\dots , L_k'')\) of label sets of \(H_1\) and \(H_2\). For each such iteration we add to \(P(H,L_1, \dots , L_k)\), where \(L_j = L_j'\cup L_j''\) for all \(j\in [k]\), the elements of the set \(\{\mathbf {q_1}+\mathbf {q_2}\mid \mathbf {q_1}\in P(H_1,L_1',\dots , L_k'), \mathbf {q_2}\in P(H_2,L_1'', \dots , L_k'')\}\) in time \((Q+1)^{2k}\). Hence, the overall time complexity for a graph H in Case 2 is \({{\mathcal {O}}}(4^{k\ell }(Q+1)^{2k})\). For the remaining three cases, we estimate the running time separately for each set \(P(H,L_1,\ldots , L_k)\). The expressions in the formulas for computing \(P(H,L_1,\ldots , L_k)\) can be evaluated in time \({\mathcal {O}}(k\ell )\) in Case 1, in time \({{\mathcal {O}}}(k\ell +(Q+1)^{k})\) in Case 3, and in time \({{\mathcal {O}}}(k\ell \cdot 3^k\cdot (Q+1)^{k})\) in Case 4. Since Case 4 dominates the other two cases, the overall time complexity for a graph H resulting from Cases 1, 3, and 4 is given by \({{\mathcal {O}}}(2^{k\ell } \cdot k\ell \cdot 3^k(Q+1)^{k})\). Since \(k\ell \le 2^{k\ell }\) and \(3^k\le (Q+1)^{k}\) for all \(Q\ge 2\), the overall time complexity of Cases 1, 3, and 4 is dominated by the effort for Case 2, which yields the claimed running time bound. (The special case \(Q=1\) would imply that for each agent, only one item has a non-zero profit. This could be solved trivially in time \({\mathcal {O}}(k)\).) \(\square \)

We conclude this section with some remarks about another, more general solution approach to Fair k-Division Under Conflicts for graphs of bounded clique-width. The unweighted version of Fair k-Division Under Conflicts (in its decision version) takes a graph G and an integer q as input and asks about the existence of a partial k-coloring in G in which all the color classes have cardinality at least q. The existence of a pseudo-polynomial time algorithm for this problem on graphs with bounded clique-width follows from a metatheorem of Courcelle and Durand (Courcelle and Durand 2016, Theorem 27), and it is plausible that with a suitable adaptation of their approach, a solution for the general Fair k-Division Under Conflicts problem might also be developed. However, as the algorithms constructed in Courcelle and Durand (2016) are very general, their running times are not specified precisely. In contrast, our algorithm given in the proof of Theorem 4 is directly tailored for Fair k-Division Under Conflicts and it is not difficult to analyze its running time.

4 Graphs of bounded tree-independence number

A tree decomposition of a graph G is a pair \((T, \{B_t\}_{t\in V(T)})\) consisting of a tree T and an assignment of a set \(B_t\subseteq V(G)\) called a bag to each node of T such that (i) every vertex of G is contained in a bag, (ii) for every edge \(\{u,v\}\in E(G)\) there exists a bag containing both u and v, and (iii) for every vertex \(u\in V(G)\) the subgraph of T induced by the set \(\{t\in V(T):\,u\in B_t\}\) is connected. In our previous work (Chiarelli et al. 2023), pseudo-polynomial algorithms for Fair k-Division Under Conflicts were developed for the case when the conflict graph is either chordal or has bounded treewidth. Both algorithms are based on a dynamic programming approach along a tree decomposition of the conflict graph. In the case of chordal graphs, each bag is a clique, while in the case of bounded treewidth, bags of the tree decomposition have bounded cardinality. In both cases, the approach works because any optimal solution, that is, a partial k-coloring \((X_1,\ldots , X_k)\) of G, intersects each bag only in a bounded number of vertices.

This key property allows in fact for a generalization of both algorithms in a unified way, by requiring the conflict graph G to be equipped with a tree decomposition with bounded independence number, that is, the maximum size of an independent set of G contained in a bag. The minimum independence number of a tree decomposition of a graph G is called the tree-independence number of G and denoted by \(\textsf{tree} \text {-} \alpha (G)\). This parameter was introduced independently by Yolov (2018) and by Dallard et al. (2022a). Graph classes with bounded treewidth have bounded tree-independence number, but bounded tree-independence number also holds for several classes of dense graphs such as chordal graphs, circular-arc graphs, or more generally H-graphs, that is, intersection graphs of connected subgraphs of a subdivision of a fixed multigraph H (see Bíró et al. 1992; Chaplick et al. 2021a, b; Fomin et al. 2020) or intersection graphs of connected subgraphs of a graph with bounded treewidth (Bodlaender et al. 1998), classes of graphs in which all minimal separators are of bounded size (Skodinis 1999), and classes of graphs excluding a single fixed graph H as an induced minor, where H is either \(K_5^-\), \(W_4\), or a complete bipartite graph \(K_{2,n}\) for some n (Dallard et al. 2022b). Furthermore, several recent works (see de Berg et al. 2020; Fomin and Golovach 2021; Jacob et al. 2022) use tree decompositions with special properties of bags that imply bounded tree-independence number.

Yolov (2018); Dallard et al. (2022a), and Milanič and Rza̧żewski (2022) identified several algorithmic problems that can be solved in polynomial time if the input graph is equipped with a tree decomposition with bounded independence number. These include the Maximum Weight Independent Packing problem, which is a common generalization of the Independent Set and Induced Matching problems, and the problem of finding a large induced sparse subgraph satisfying an arbitrary but fixed property expressible in counting monadic second-order logic. As shown by Dallard et al. (2022c), for every constant \(k \ge 4\) it is NP-complete to decide if a given graph has tree-independence number at most k. However, for algorithmic applications of bounded tree-independence number, this is not necessarily an obstacle, since Dallard et al. also gave an algorithm that, given an n-vertex graph G and an integer k, in time \(2^{{\mathcal {O}}(k^2)}n^{{\mathcal {O}}(k)}\) either outputs a tree decomposition of G with independence number at most 8k, or determines that the tree-independence number of G is larger than k.

The approach developed in our previous work (Chiarelli et al. 2023) leading to dynamic programming algorithms for Fair k-Division Under Conflicts in chordal graphs and graphs with bounded treewidth can also be used to prove the following more general result.

Theorem 5

For every two positive integers k and \(\ell \), Fair k-Division Under Conflicts is solvable in time \({\mathcal {O}}(bn^{k\ell +1}(Q+1)^{2k})\) if the input n-vertex conflict graph G is equipped with a tree decomposition with b bags and independence number at most \(\ell \), where \(Q = \max _{1\le j\le k}p_j(V(G))\).

Proof

The approach is a straightforward adaptation of the approach used in Sections 3.3 and 3.4 of Chiarelli et al. (2023), hence we only explain the main ideas. Given a tree decomposition of G with b bags and independence number at most \(\ell \), we first invoke (Dallard et al. 2022a, Lemma 5.1) to compute in time \({\mathcal {O}}(n^2b)\) a nice rooted tree decomposition \({\mathcal {T}} = (T, \{B_t\}_{t\in V(T)})\) of G with \({\mathcal {O}}(nb)\) bags and independence number at most \(\ell \) (we refer to Cygan et al. (2015) for the definition of a nice tree decomposition). For a node t of T, let \(V_t\) denote the union of all bags \(B_{t'}\) such that \(t'\in V(T)\) is a (not necessarily proper) descendant of t in T. In our dynamic programming approach, we then traverse the tree T bottom-up and compute, for every node \(t\in V(T)\) and every partial k-coloring c of the subgraph of G induced by \(B_t\), the family P(t, c) of all profit profiles of partial k-colorings of the graph \(G[V_t]\) that agree with c on \(B_t\). The maximum satisfaction level over all profit profiles in the set P(c, t) where t is the root of T will give the optimal value of Fair k-Division Under Conflicts for (\(G,p_1,\ldots , p_k)\).

Time complexity analysis. Since each bag induces a subgraph with independence number at most \(\ell \), each partial k-coloring \(c = (X_1,\ldots , X_k)\) of the subgraph of G induced by \(B_t\) satisfies \(|X_j|\le \ell \) for all \(j\in [\ell ]\). It follows that the number of such partial k-colorings is bounded by \({\mathcal {O}}(n^{k\ell })\). For a given node t of T and a partial k-coloring c of \(G[B_t]\), the family P(t, c) of profit profiles of partial k-colorings of the graph \(G[V_t]\) that agree with c on \(B_t\) can be computed from the analogous families already computed at the children of t (if any). This is done using exactly the same recurrence relations as the ones used for graphs of bounded treewidth, see Section 3.4 of Chiarelli et al. (2023). Indeed, the proof of correctness of those relations does not depend on the structure of the subgraphs induced by the bags, the only difference resulting from replacing bounded treewidth with bounded tree-independence number is in the running time. For a given node t of T and a partial k-coloring c of \(G[B_t]\), the set P(t, c) can be computed in time \({\mathcal {O}}((Q+1)^{2k})\). Since T has \({\mathcal {O}}(b n)\) nodes and for each node t there are \({\mathcal {O}}(n^{k\ell })\) partial k-colorings c of the graph \(G[B_t]\), the total number of families P(t, c) to compute is of the order \({\mathcal {O}}(b n^{k\ell +1})\). The claimed time complexity of the algorithm follows. \(\square \)

The case of chordal graphs corresponds to \(\ell = 1\) and \(b ={\mathcal {O}}(n)\) (see, e.g., Spinrad 2003) and indeed, for these values of \(\ell \) and p, Theorem 5 implies (Chiarelli et al. 2023, Theorem 19). For graphs of bounded treewidth, Theorem 5 also implies a pseudo-polynomial algorithm, although its running time does not match the corresponding tailor-made result of Chiarelli et al. (2023, Theorem 20).

5 Conclusions

In this paper, we continued the study of the computational complexity of Fair k-Division Under Conflicts introduced in our previous paper (Chiarelli et al. 2023). We managed to contribute three new dynamic programming algorithms running in pseudo-polynomial time and allowing the construction of an FPTAS. First, we answered a question posed in Chiarelli et al. (2023) by giving an algorithm for convex bipartite conflict graphs. This extends the earlier result for biconvex bipartite graphs, although it employs a totally different algorithmic strategy. Second, we gave algorithms for conflict graphs of bounded clique-width or bounded tree-independence number. These results replace the previously derived algorithm for graphs of bounded treewidth as the currently most general positive results for non-perfect conflict graphs. Note that all of these dynamic programming algorithms also permit the construction of fully polynomial time approximation schemes (FPTAS).

It would be interesting to identify further graph width parameters leading to pseudo-polynomial algorithms for Fair k-Division Under Conflicts and similar problems. One such parameter, kindly brought to our attention by an anonymous reviewer, is thinness (see Mannino et al. (2007)), for which the framework of (Bonomo and de Estrada 2019) can be adapted to problems such as Fair k-Division Under Conflicts, leading to an alternative pseudo-polynomial-time algorithm for the class of convex bipartite graphs, and even for the more general class of interval bigraphs (Rafiey 2022), which have thinness at most 2 (see Bonomo-Braberman and Brito 2023). This answers another question posed in Chiarelli et al. (2023).

A natural width parameter, more general than thinness and possibly also leading to pseudo-polynomial algorithms for Fair k-Division Under Conflicts, is mim-width (see Jaffke et al. 2020), as suggested to us by Andrea Munaro (personal communication, 2020). An algorithmic metatheorem for this parameter was recently developed by Bergougnoux et al. (2023); however, the theorem does not capture max–min problems such as Fair k-Division Under Conflicts and it is an interesting question whether an appropriate adaptation is possible.

Finally, since Fair k-Division Under Conflicts is \(\text {NP}\)-hard on general bipartite conflict graphs (see Chiarelli et al. 2023), using the following chain of inclusions: convex bipartite \(\subseteq \) interval bigraph \(\subseteq \) chordal bipartite \(\subseteq \) bipartite, we see that the complexity of Fair k-Division Under Conflicts in the class of chordal bipartite graphs remains an interesting open problem for future research.