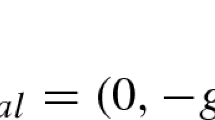1 Introduction

Many efforts have been devoted to including dispersive effects in models in fluid mechanics, and in particular, they have been widely studied in the context of shallow flows in the literature. There are essentially two approaches to consider dispersive effects in this framework: Boussinesq type systems and non-hydrostatic systems.

Boussinesq type systems are mainly based on classic shallow water system, whose unknowns are the total height of the fluid and the horizontal velocity. The system is then extended by introducing high order derivatives of the variables. The two pioneering works on Boussinesq models were proposed by Boussinesq (1872) and Peregrine (1967). Some other models were proposed afterwards: Madsen et al. (1991); Madsen and Sørensen (1992), Nwogu (1993), Serre (1953), Green and Naghdi (1976), Schäffer and Madsen (1995), Lannes and Bonneton (2009), among many others. For a review on Boussinesq type dispersive models, see Lannes (2013), Kirby (2016).

Contrary to Boussinesq systems, non-hydrostatic models only consider first order derivatives of the variables but with a larger number of unknowns. Usually, in addition to the water depth and horizontal velocity, we find the vertical velocity, non-hydrostatic pressure, and other unknowns related to the vertical profile of the different variables. One of the essential points of these models is the presence of constraint equations related to the incompressibility condition, see for example Yamazaki et al. (2008) and Bristeau et al. (2015).

Although both approaches seem quite different, in many cases they are equivalent, as it was shown in Escalante and Morales de Luna (2020). They introduced a general formulation that relates some well-known classic Boussinesq systems and non-hydrostatic models. Concretely, it was shown that many of these classic Boussinesq systems might be written as non-hydrostatic models. We want to point out that the non-hydrostatic formulation has several advantages from the numerical point of view. In particular, avoiding high order derivatives makes the numerical approximation easier. Moreover, the treatment of boundary conditions is also more straightforward.

A strategy to improve the dispersion relation of such systems is to increase the accuracy of the vertical profile for both velocity and pressure components. For this purpose, several attempts have also been introduced in the literature. The so-called multilayer approach considers non-material vertical interfaces, dividing the fluid into virtual vertical layers. Different profiles for the velocity and pressure within each layer may be assumed. Notice that the term multilayer has been used sometimes for stratified flow models, where one considers a constant density within each layer. This has no relation with the approach we are considering in this paper. To avoid any possible confusion, in Fernández-Nieto et al. (2018) it was proposed to name the former (non-stratified flows) as layer-averaged models. We shall do the same in what follows.

In Sainte-Marie (2011), a non-hydrostatic layer-averaged model is proposed, which corresponds to the extension of the hydrostatic model in Audusse et al. (2011). The momentum equations are approximated by considering a constant vertical profile for horizontal and vertical velocity components. Then, velocity may be discontinuous at the interfaces, although the pressure profile is supposed to be continuous. However, a linear profile of the vertical velocity within each layer is considered to approximate the incompressibility condition, which is a compatible condition of strong solutions in each layer for this equation.

A similar model was proposed in Bai and Cheung (2013), which assumes a constant profile for the horizontal velocity and linear profiles for the vertical velocity and pressure. The common ground for both references is that the horizontal velocity has a constant vertical profile within each layer and may be discontinuous at the interfaces. A different assumption is found in Lynett and Liu (2004a), where a layer-averaged model is derived by using a continuous global profile of the horizontal velocity, which is quadratic within each layer.

In Fernández-Nieto et al. (2018), a hierarchy of models is presented, with an associated energy balance, where again a constant profile is assumed for the horizontal velocity inside each layer. At the same time, several degrees of freedom are introduced for the vertical velocity and pressure, accounting for the vertical approximation of such variables. In that work, the linear dispersion relation was studied for the different models proposed. It was shown that the dispersion relation converges to the exact dispersion relation for Euler equations when the number of layers goes to infinity. A numerical strategy to solve these models is proposed in Escalante-Sanchez et al. (2021). Let us recall the notation of the models introduced in that paper as it will be helpful in what follows. These models are named as LDNH\(_k\) where LDNH stands for Layerwise Discretisation Non-Hydrostatic, and k is the order of approximation. More precisely, LDNH\(_0\) may be seen as a generalisation of models Yamazaki et al. (2008) and Bristeau et al. (2015), while LDNH\(_2\) is as a generalisation of the Serre–Green–Naghdi model. LDNH\(_1\) is an in-between intermediate model. Similarly, in Cantero-Chinchilla et al. (2018) authors derived a weighted-averaged non-hydrostatic pressure model, under the assumption of linear horizontal velocity, whereas the vertical velocity and the non-hydrostatic pressure was assumed to have a quadratic profile.

This paper focuses on the derivation of 2D layer-averaged models where the vertical profile of the horizontal velocity is supposed to be layerwise linear and discontinuous at the interfaces. The extension to 2D is straightforward. Concretely, a family (with respect to the degree of approximation of the vertical velocity and pressure) of novel models is introduced, named as LIN-NH\(_k\) models for \(k=0,1,2\), where the index k corresponds to the degree of approximation of the vertical velocity in the vertical momentum equation. Therefore, three models are proposed, based on three different profiles for the pressure, which are related to the approximation of the vertical momentum equation and the incompressibility condition. In addition, the pressure profile is considered as a polynomial of degree \(k+1\). All the proposed non-hydrostatic models also satisfy a dissipative energy balance. As we show in this paper, since more unknowns are introduced, linear dispersion relation, group velocity, and linear shoaling are greatly improved for such models. In particular, the LIN-NH\(_1\) and LIN-NH\(_2\) models exhibit excellent results for these dispersive properties. Moreover, another contribution is a general procedure to compute the group velocity and shoaling gradient from the dispersion relation for the wave celerity.

Although a general formulation based on a vertical Galerkin approach, i.e. polynomials with an arbitrary degree describing the vertical profile of the variables, is possible from the theoretical point of view (see Garres-Díaz et al. 2023 for the hydrostatic case), we remains here in the case of first order polynomials for the horizontal velocity. Going to the general case in this non-hydrostatic framework would lead to excessively complicated models, where we would also have an arbitrary (high) number of unknowns associated to the pressure needed, and therefore also of constraints related to the incompressibility condition. Moreover, to our point of view, this model, that is expected to be second order accurate in the vertical direction, is a good compromise between simplicity and accuracy, being already an important improvement with respect to previous multilayer non-hydrostatic systems where the horizontal velocity is supposed to be always constant (and therefore first-order accurate in the vertical direction).

In addition, the models proposed in this work can be seen as second order Galerkin vertical discretisations of Euler system. The main difference with respect to a fully Galerkin discretisation is the fact that we obtain a model depending only on the horizontal space variable. As a consequence, more efficient numerical methods may be designed. Actually, a specific and efficient numerical method was proposed for the layer-averaged LDNH models in Escalante-Sanchez et al. (2021). Here, we only focus on the deduction of the LIN-NH models and its properties. Taking into account the key role of designing efficient methods for the proposed models, it is out of the scope of this paper and must be addressed in the future.

The paper is organised as follows. In Sect. 2, we state the notation and the layer-averaged procedure for the layerwise linear horizontal velocity case. Section 2.1 focuses on the discrete spaces and hypotheses over the vertical profile of each variable (horizontal and vertical velocities and pressure), as well as the normal jump condition at the interfaces associated with the weak formulation of the Euler system. In Sect. 2.2 we describe the vertical averaging of the mass and horizontal momentum equations without detailing the pressure terms. Section 3 is devoted to derive the cascade of LIN-NH\(_k\) non-hydrostatic models, for \(k=0,1,2\). The dispersive properties for these models are analysed in Sect. 4, and some conclusions are presented in Sect. 5. Finally, Appendix A contains a summary of all the models LIN-NH introduced in this work and the models LDNH proposed in Fernández-Nieto et al. (2018), including the layerwise vertical profile of the unknowns, and the coefficients of the dispersion relation associated to each model.

2 Initial system and layer-averaged approach

This section introduces the general settings associated with the layer-averaged approach for the Euler equations. In this work we shall assume a piecewise linear approximation of the horizontal velocity.

This layer-averaged approach can be seen as a technique to approximate the solution of the Euler equations in the framework of the Discontinuous Galerkin methods. The final model that we obtain is a system of partial differential equations. The solution of this system may be seen as a particular weak solution of Euler equations, in the sense that it corresponds to an approximated piecewise smooth weak solution that may be discontinuous at the internal interfaces. We remark that these interfaces are not physical or material interfaces. They represent a virtual decomposition or partition of the domain vertically. The procedure is as follows: first, we consider a vertical discretisation. Second, a layer-averaging approach is considered assuming an appropriate structure of the weak solutions. In particular, here, we shall assume that the velocity vector has horizontal components that are linear in the vertical z-direction within each layer. Third, some closure relations (or constraints) are needed, and they will be presented later in Sect. 3.1.

For the sake of simplicity, we shall consider here a 2-dimensional space, where the space variables are denoted by \((x,z)\in {\mathbb {R}}^2\). Nevertheless, it could be extended easily to the 3D case. In what follows, \(\smash {\nabla = (\partial _{x}, \partial _{z})}\) represents the usual differential operator. Let us consider now an incompressible fluid with constant density \(\rho \in {\mathbb {R}}\). Let us denote \(g\in {\mathbb {R}}\) the gravity acceleration, \(p \in {\mathbb {R}}\) the pressure, \({\varvec{U}}= (u,w)^{'} \in {\mathbb {R}}^2\) the velocity vector, and a moving domain

$$\begin{aligned} \Omega (t) = \Big \{(x,z): \; z_b(x)< z <z_b(x)+H(t,x)\Big \}, \end{aligned}$$

where the topography \(z_b\) is assumed to be independent from time and H the water height (see Fig. 1). The Euler system is written, for \((x,z)\in \Omega (t)\), as

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}\rho + \nabla \cdot \left( \rho \, {{{\varvec{U}}}}\right) = 0,\\ \partial _{t}\left( \rho \, {{{\varvec{U}}}}\right) + \nabla \cdot \left( \rho \, {{{\varvec{U}}}}\otimes {{{\varvec{U}}}} + p{\varvec{I}}\right) = \rho \, {\varvec{g}}, \end{array}\right. } \end{aligned}$$
(1)

where \({\varvec{g}}= (0, -g)^{'} \in {\mathbb {R}}^2\) and \(\smash {\varvec{I}}\) is the identity matrix. Notice that we write the time derivative of the density in previous system, despite of assuming the case of an incompressible fluid. It is done for the sake of clarity and generality when writing the normal jump conditions associated to the layer-averaging approach. The system is completed with initial and boundary conditions, and the following kinematic conditions:

$$\begin{aligned}{} & {} \partial _tH+ {\varvec{U}}|_{z=z_b+H} \cdot \nabla \left( z_b+H-z\right) =0, \end{aligned}$$
(2)
$$\begin{aligned}{} & {} {\varvec{U}}|_{z=z_b} \cdot \nabla \left( z_b-z\right) =0. \end{aligned}$$
(3)
Fig. 1
figure 1

Sketch of the vertical partition of the fluid domain

Full size image

Now, to apply the layer-averaged approach, the domain is subdivided along the vertical direction into \(L\in {\mathbb {N}}\) layers with thickness \(\smash h_{\alpha }(t,x)\), which are denoted by \(\Omega _\alpha (t)\). The layers are separated by \(L+1\) interfaces \({\mathcal {L}}_{{\alpha +1/2}}(t)\), defined by \(z = \smash z_{\alpha +1/2}(t,x)\) for \(\smash \alpha =0,1,\ldots ,L\). The interfaces are assumed sufficiently smooth, at least \(C^1\) (see Fig. 1). More explicitly,

$$\begin{aligned} \Omega _{\alpha }(t) = \Big \{(x,z): \; z_{\alpha -1/2}(t,x)< z <z_{\alpha +1/2}(t,x)\Big \}. \end{aligned}$$

Notice then that

$$\begin{aligned} z_{\alpha +1/2}= z_{b} + \sum _{\beta =1}^\alpha h_{\beta },\qquad \text{ for } \alpha =1,\dots ,L, \end{aligned}$$

where \(z_b = z_{1/2}\) and \(h_{\alpha }=z_{\alpha +1/2}- z_{\alpha -1/2}\). Moreover, the total height of the fluid is equal to

$$\begin{aligned} H = \sum _{\alpha =1}^L h_\alpha , \quad \text { with } h_\alpha =\ell _\alpha H, \text { where } {(\ell _\alpha )}_{\{\alpha \in 1,\ldots ,L\}} \text { are such that } \ell _\alpha \in [0,1],\;\sum _{\alpha =1}^L\ell _\alpha =1.\nonumber \\ \end{aligned}$$
(4)

Let us also denote by \(z_\alpha \) the midpoint of the layer \(\Omega _\alpha \), i.e.,

$$\begin{aligned} z_\alpha =\frac{z_{{\alpha -1/2}}+z_{{\alpha +1/2}}}{2} = z_{\alpha -1/2} + \displaystyle \frac{h_\alpha }{2}, \qquad \text { for }\alpha =1,\dots ,L. \end{aligned}$$

Furthermore, let us introduce the following notations: for any function f(t, x, z), we define:

  • Its approximations at the interfaces \({\mathcal {L}}_{{\alpha +1/2}}\) for \(\smash \alpha =0,\ldots ,L\)

    $$\begin{aligned} f_{\alpha +1/2}^{-} = \lim _{\begin{array}{c} z\rightarrow z_{\alpha +1/2}\\ z<z_{\alpha +1/2} \end{array}} f_{|_{\Omega _{\alpha }}}, \qquad f_{\alpha +1/2}^{+} = \lim _{\begin{array}{c} z\rightarrow z_{\alpha +1/2}\\ z>z_{\alpha +1/2} \end{array}} f_{|_{\Omega _{\alpha +1}}}. \end{aligned}$$

    In the case of continuous functions, we shall simply write \(f_{{\alpha +1/2}} = f_{{\alpha -1/2}}^+= f_{{\alpha +1/2}}^-\);

  • The average value over the layer \(\Omega _\alpha \)

    $$\begin{aligned} \overline{f}_\alpha (t,x) =\displaystyle \frac{1}{h_\alpha }\displaystyle \int _{z_{\alpha -1/2}}^{z_{{\alpha -1/2}}} f(t,x,z)\, \textrm{d}z; \end{aligned}$$
    (5a)

  • The linear average of f over the layer \(\Omega _\alpha \)

    $$\begin{aligned} \widehat{f}_\alpha = \displaystyle \frac{f_{\alpha -1/2}^+ +f_{\alpha +1/2}^-}{2}; \end{aligned}$$
    (5b)

  • The variation through the layer \(\Omega _\alpha \)

    $$\begin{aligned} (\delta f)_\alpha = f_{\alpha +1/2}^- - f_{\alpha -1/2}^+; \end{aligned}$$
    (5c)

  • The average value through the interface \({\mathcal {L}}_{\alpha +1/2}\)

    $$\begin{aligned} \widetilde{f}_{\alpha +1/2}= \displaystyle \frac{f_{\alpha +1/2}^+ +f_{\alpha +1/2}^-}{2}; \end{aligned}$$
    (5d)

  • The jump across the interface \({\mathcal {L}}_{{\alpha +1/2}}\)

    $$\begin{aligned}{}[f]_{{\alpha +1/2}} = f_{\alpha +1/2}^+ - f_{\alpha +1/2}^-. \end{aligned}$$
    (5e)

Note that, in general, \(\overline{f}_\alpha \ne \widehat{f}_\alpha \), but the equality holds if f is constant or linear in z over the layer \(\Omega _\alpha \).

2.1 Layerwise approximation of the variables and normal jump conditions

This subsection deals with the main hypotheses upon velocity and pressure fields in the layer-averaged framework. In particular, we detail here the vertical profile for the variables considered in this work and its notation. We also write the normal jump condition associated with the weak formulation.

2.1.1 Choice of discrete spaces for velocity and pressure fields

The layer-averaged models presented in Fernández-Nieto et al. (2013, 2016) assume that the horizontal velocity is constant in the z-direction within each layer. In practice, this will formally limit us to first order approximations of the solution for the Euler equations. In this work we shall consider a piecewise linear profile in z for the horizontal velocity. Concerning the other variables, a piecewise parabolic profile in z is supposed for the vertical velocity, and a piecewise third order polynomial in z is used for the non-hydrostatic pressure. Nevertheless, some other alternative simplified equations will be presented afterwards, resulting in simplified models.

More explicitly, let us specify the discretisation assumptions for the velocity unknowns

$$\begin{aligned} {\varvec{U}}_{\alpha }:= {\varvec{U}}_{|_{\Omega _{\alpha }}}:= (u_{\alpha }, w_{\alpha })^{'}, \end{aligned}$$

where \(u_{\alpha }\) and \(w_{\alpha }\) are the horizontal and vertical components of the velocity field in layer \(\Omega _\alpha \). Then, the following profiles and notation are chosen for this model:

Horizontal velocity: a linear profile on the vertical direction is assumed within each layer

$$\begin{aligned} u_\alpha (t,x,z)=\overline{u}_\alpha (t,x)+\lambda _\alpha (t,x)\bigl (z-z_\alpha (t,x)\bigr ), \text { for } z \in [z_{\alpha -1/2}(t,x),z_{\alpha +1/2}(t,x)], \end{aligned}$$
(6)

where \(\overline{u}_\alpha \) and \(\lambda _\alpha \) are the averaged horizontal velocity and the slope respectively in the z direction. In what follows and for the sake of simplicity, we shall not write the dependence of the variables on (t, x) explicitly unless necessary. It follows then that the limit at the interfaces \(u_{{\alpha +1/2}}^-\) and \(\ u_{{\alpha -1/2}}^+\) are obtained by evaluating (6) at \(z_{\alpha +1/2}\) and \(z_{\alpha -1/2}\), respectively, i.e.,

$$\begin{aligned} u_{\alpha +1/2}^-=\overline{u}_\alpha +\frac{h_\alpha \lambda _\alpha }{2}, \qquad u_{\alpha -1/2}^+=\overline{u}_\alpha -\frac{h_\alpha \lambda _\alpha }{2}. \end{aligned}$$
(7)

Vertical velocity: focusing on the incompressibility condition and given the piecewise linear profile (6) for the horizontal velocity, a compatibility criterion leads us to consider a piecewise parabolic polynomial in z, that is

$$\begin{aligned} w_\alpha (z) = w_\alpha (z_\alpha ) + \varphi _\alpha \left( z-z_\alpha \right) + \displaystyle \frac{\psi _\alpha }{2}\left( z-z_\alpha \right) ^2, \quad \text {for } z \in [z_{\alpha -1/2},z_{\alpha +1/2}]. \end{aligned}$$
(8)

Hence, there are three parameters to set. On the one hand, the integration of (8) over the layer yields

$$\begin{aligned} w_\alpha (z_\alpha )=\overline{w}_\alpha -\frac{h_\alpha ^2\psi _\alpha }{24}. \end{aligned}$$
(9)

Note that \(w_\alpha (z_\alpha ) \ne \overline{w}_\alpha \) in this case because of the contribution of the second-order term.

On the other hand, a second-order Taylor expansion, which is exact for a quadratic function, yields

$$\begin{aligned} w_{\alpha }(z) = w_\alpha (z_\alpha ) + \left( \partial _z w_\alpha \right) _{|_{z=z_\alpha }} \left( z-z_\alpha \right) + \left( \partial _{zz}^2 w_{\alpha }\right) _{|_{z=z_\alpha }} \frac{(z-z_\alpha )^2}{2}, \quad \text { for } \smash \alpha =1,\ldots ,L. \end{aligned}$$

As we want \(w_\alpha \) to approximate \(w_{|\Omega _\alpha }\), let us mimic the incompressibility constraint \(\partial _zw=-\partial _xu\) using (6). Hence we impose

$$\begin{aligned} \left( \partial _z w_{\alpha }\right) _{|_{z=z_\alpha }} = - \partial _x \overline{u}_{\alpha } + \lambda _{\alpha } \partial _x z_\alpha , \quad \text {and}\quad \left( \partial _{zz}^2 w_{\alpha }\right) _{|_{z=z_\alpha }} = - \partial _{x} \lambda _\alpha . \end{aligned}$$
(10)

Therefore, combining (8), (9) and (10), we get

$$\begin{aligned} w_{\alpha }(z) = \overline{w}_\alpha +\varphi _\alpha (z-z_\alpha )+ \frac{\psi _\alpha }{2}\left( (z-z_\alpha )^2-\frac{h_\alpha ^2}{12}\right) , \end{aligned}$$
(11)

for \(\smash \alpha =1,\ldots ,L\), with

figure a

Evaluating (11) at \(z_{\alpha \pm 1/2}\), we obtain

$$\begin{aligned} w_{\alpha +1/2}^-=\overline{w}_\alpha +\frac{h_\alpha \varphi _\alpha }{2} +\frac{h_\alpha ^2\psi _\alpha }{12}, \qquad w_{\alpha -1/2}^+=\overline{w}_\alpha -\frac{h_\alpha \varphi _\alpha }{2} +\frac{h_\alpha ^2\psi _\alpha }{12}. \end{aligned}$$
(13)

Pressure: the total pressure is decomposed into a hydrostatic part \(g \left( z_b+H - z\right) \), and a non-hydrostatic counterpart q:

$$\begin{aligned} p=\rho \left( g \left( z_b+H - z\right) + q\right) , \end{aligned}$$

where we assume that the pressure is known at the surface, which is usually set to zero.

As mentioned above, we choose a layerwise linear horizontal velocity and a layerwise parabolic vertical velocity (potentially discontinuous across the interfaces). Consequently, the pressure must be a layerwise cubic function due to the vertical momentum equation. We assume in the present work that the pressure is continuous across interfaces.

Hence, we are looking for a 3rd-order polynomial \(q_\alpha \) which satisfies the following requirements:

$$\begin{aligned} q_\alpha (z_{\alpha \pm 1/2})=q_{\alpha \pm 1/2}, \quad \text { and } \quad \partial _z q_\alpha (z_\alpha )=\frac{\pi _\alpha }{h_\alpha }. \end{aligned}$$

Together with the definitions (5), this leads to

$$\begin{aligned} q_\alpha (z)=\displaystyle \frac{3\overline{q}_\alpha - \widehat{q}_\alpha }{2} + \pi _\alpha \frac{z-z_\alpha }{h_\alpha } + 6\left( \widehat{q}_\alpha -\overline{q}_\alpha \right) \frac{(z-z_\alpha )^2}{h_\alpha ^2} + 4\bigl ((\delta q)_\alpha - \pi _\alpha \bigr )\frac{(z-z_\alpha )^3}{h_\alpha ^3},\nonumber \\ \end{aligned}$$
(14)

for \(z \in [z_{\alpha -1/2},z_{\alpha +1/2}]\).

2.1.2 Jump conditions and evolution equation for the layer midpoints

Following Fernández-Nieto et al. (2013), the model is deduced by looking for a particular piecewise smooth weak solution \(\left( \rho ,{\varvec{U}},p\right) \) of system (1). More explicitly, we search for a solution that satisfies the weak formulation of the system for a particular set of tests functions. We refer to Fernández-Nieto et al. (2013) for further details. In particular, they correspond to a classic, smooth solution inside each layer \(\Omega _\alpha \), while it should satisfy the normal flux jump conditions across the interfaces \({\mathcal {L}}_{{\alpha +1/2}}\), \(\alpha =0,\ldots , L\).

The jump condition for the mass conservation law reads

$$\begin{aligned} {\left[ (\rho ;\rho {{\varvec{U}}})\right] }_{{\alpha +1/2}}\, \cdot \, \left( \partial _{t}z_{\alpha +1/2}, \partial _x z_{\alpha +1/2}, -1\right) = 0, \end{aligned}$$
(15a)

and for the momentum conservation law

$$\begin{aligned} {\left[ ( \rho {{\varvec{U}}};\rho {{\varvec{U}}}\otimes {{\varvec{U}}}-p {\varvec{I}})\right] }_{{\alpha +1/2}}\, \cdot \, \left( \partial _{t}z_{\alpha +1/2}, \partial _x z_{\alpha +1/2}, -1\right) = 0. \end{aligned}$$
(15b)

We are considering here a constant density for the fluid. Hence, following Fernández-Nieto et al. (2013), (15a) implies

$$\begin{aligned} \Gamma _{{\alpha +1/2}}:= \Gamma _{{\alpha +1/2}}^- =\Gamma _{{\alpha +1/2}}^{+}, \end{aligned}$$
(16a)

where \(\Gamma _{{\alpha +1/2}}\) is the mass transfer term through the interface \({\mathcal {L}}_{{\alpha +1/2}}\) given by

$$\begin{aligned} \Gamma _{{\alpha +1/2}}^{\pm } \,=\, -\partial _{t}z_{\alpha +1/2}\,-\, u_{\alpha +1/2}^\pm \partial _x z_{\alpha +1/2}\,+\, w_{{\alpha +1/2}}^\pm . \end{aligned}$$
(16b)

In particular, using previous equation for \(\Gamma _{\alpha \pm 1/2}\) and making the average, we infer that

$$\begin{aligned} \partial _t z_\alpha + \overline{u}_\alpha \partial _x z_\alpha = {\widehat{w}}_\alpha - \frac{h_\alpha }{4} \lambda _\alpha \partial _x h_\alpha -\frac{\Gamma _{\alpha -1/2}+\Gamma _{\alpha +1/2}}{2}, \end{aligned}$$
(17)

which gives the evolution of the midpoint at each layer \(\Omega _{\alpha }\).

2.2 Layer-averaged approximation: mass and horizontal momentum equations

In this section we obtain the mass and horizontal momentum equations of the target model by a layer-averaged process. In what follows, we use a general depth-integration process for mass and horizontal momentum equations.

Mass conservation The incompressibility condition is integrated over each layer, which leads to

$$\begin{aligned} 0= & {} \displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} \nabla \cdot {{\varvec{U}}}_\alpha \, {\textrm{d}} z = \partial _x\left( \displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}}u_\alpha \left( t,x,z\right) {\textrm{d}}z \right) \\{} & {} \quad -\; u_{{\alpha +1/2}}^{-}\partial _x z_{\alpha +1/2}+\; u_{{\alpha -1/2}}^{+}\partial _x z_{\alpha -1/2}\;+\; {w}_{{\alpha +1/2}}^- - {w}_{{\alpha -1/2}}^+. \end{aligned}$$

Taking into account the definition of the mass transfer terms (16), we obtain the mass conservation laws

$$\begin{aligned} \partial _{t}h_{\alpha } + \partial _x\left( h_{\alpha } \overline{u}_{\alpha }\right) = \Gamma _{{\alpha -1/2}} - \Gamma _{{\alpha +1/2}}, \qquad \qquad \alpha =1,\ldots ,L, \end{aligned}$$
(18)

where we recall that \(\Gamma _{\alpha \pm 1/2}\) account for mass transfer across interfaces \({\mathcal {L}}_{\alpha \pm 1/2}\). Actually, they can be expressed in terms of the velocities by combining previous equations, getting, for \(\alpha =1,\dots , L-1\),

$$\begin{aligned} \Gamma _{\alpha +1/2}=\sum _{\beta =\alpha +1}^{L} \partial _x\left( h_\beta \left( \overline{u}_\beta -{\overline{\overline{u}}}\right) \right) , \qquad \text{ with }\qquad {\overline{\overline{u}}}:=\sum _{\alpha =1}^L\ell _\alpha \overline{u}_\alpha , \end{aligned}$$
(19)

for \(\ell _\alpha \) defined in (4). Moreover, summing Eq. (18) over \(\alpha \) we get

$$\begin{aligned} \partial _tH+\partial _x\left( H{{\overline{\overline{u}}}}\right) =0. \end{aligned}$$
(20)

Therefore, it is equivalent to considering Eq. (18) and the set of equations defined by (19) and (20).

Note that \(\Gamma _{1/2}\) and \(\Gamma _{L+1/2}\) correspond to the mass exchange at the free surface and the bottom, respectively, and they are set to zero unless specified. In any case, both of them should be provided as data.

Averaged horizontal momentum conservation. The approximation of the horizontal momentum equation is deduced in two steps. First, a layer-integration of the horizontal momentum equation provides the horizontal momentum conservation law equation related to the averaged velocity, \({\overline{u}}_{\alpha }\).

$$\begin{aligned}{} & {} \partial _{t} \left( h_\alpha {\overline{u}}_{\alpha }\right) + \partial _x \bigg ( h_\alpha \overline{u}_\alpha ^2 + \frac{h_\alpha ^3 \lambda _{\alpha }^2}{12} \bigg ) + \displaystyle \frac{1}{\rho } \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} \partial _x p_\alpha \, {\textrm{d}}z = -{\widetilde{u}}_{\alpha +1/2} \Gamma _{\alpha +1/2} + {\widetilde{u}}_{\alpha -1/2} \Gamma _{\alpha -1/2},\nonumber \\ \end{aligned}$$
(21)

see (5) for notations. Note that here we have used the jump condition (15b), otherwise a term \(u_{\alpha \pm 1/2}^\mp \) would appear instead of \({\widetilde{u}}_{\alpha \pm 1/2}\). This is done in what follows when the limit values of the horizontal and vertical velocities at the interfaces appear.

Secondly, we evaluate the mean deviation of the horizontal velocity and use (6) to derive the conservation law associated with \(\lambda _\alpha \). To do so, the horizontal momentum equation is multiplied by \(\left( z-z_\alpha \right) \) and then integrated inside the layer, yielding to

$$\begin{aligned} \partial _t \left( \frac{h_\alpha ^2\lambda _\alpha }{12}\right) + \partial _x \left( \frac{h_\alpha ^2\lambda _\alpha }{12}\overline{u}_{\alpha } \right) +\frac{h_\alpha ^2 \lambda _\alpha }{12} \partial _x \overline{u}_{\alpha } + \displaystyle \frac{1}{\rho h_\alpha }\displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} (z-z_\alpha ) \partial _x p_\alpha \, {\textrm{d}}z \nonumber \\ = \Gamma _{\alpha +1/2}\bigg ( \frac{h_\alpha \lambda _{\alpha }}{12} + \frac{\overline{u}_{\alpha }-{\widetilde{u}}_{\alpha +1/2}}{2} \bigg ) -\Gamma _{\alpha -1/2}\bigg ( \frac{h_\alpha \lambda _{\alpha }}{12} - \frac{\overline{u}_{\alpha }-{\widetilde{u}}_{\alpha -1/2}}{2} \bigg ), \end{aligned}$$
(22)

for \(\alpha = 1,\ldots ,L\).

Note that the integrals involving the pressure in (21) and (22) have not been specified. These terms will be computed later on depending on the assumption on the pressure profile. The simplest choice corresponds to the assumption of hydrostatic pressure, and this model is presented in the following subsection. Non-hydrostatic pressure models are deduced in Sect. 3.

2.3 LIN-H model: linear horizontal velocity and hydrostatic pressure

Let us mention the case of hydrostatic pressure, where the resulting model is a particular case of the multilayer-moment model presented in Garres-Díaz et al. (2023). In that case, the final system is defined by (18), (21), (22), where, as it is usual in the framework of hydrostatic shallow flows, the pressure is defined by

$$\begin{aligned} p(z)= \rho g \left( z_b+H - z\right) . \end{aligned}$$

Now, the integrals associated to the pressure in (21) and (22) are

$$\begin{aligned} \displaystyle \frac{1}{\rho }\displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} \partial _x p \, {\text {d}}z= g h_\alpha \partial _x \left( z_b+H\right) ,\qquad \text{ and }\qquad \displaystyle \frac{1}{\rho }\displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} (z-z_\alpha ) \partial _x p \, {\text {d}}z=0. \end{aligned}$$

Therefore, the final system for hydrostatic pressure is defined by the following set of equations:

$$\begin{aligned} \left\{ \begin{array}{l} \partial _{t}h_{\alpha } + \partial _x (h_\alpha \overline{u}_{\alpha } ) = \Gamma _{{\alpha -1/2}} - \Gamma _{{\alpha +1/2}},\\ \partial _{t} (h_\alpha {\overline{u}}_{\alpha }) + \partial _x \bigg ( h_\alpha \overline{u}_\alpha ^2 + \displaystyle \frac{h_\alpha ^3 \lambda _{\alpha }^2}{12} \bigg ) + g h_\alpha \partial _x (z_b+H) = - {\widetilde{u}}_{\alpha +1/2} \Gamma _{\alpha +1/2} + {\widetilde{u}}_{\alpha -1/2} \Gamma _{\alpha -1/2},\\ \partial _t \left( \displaystyle \frac{ h_\alpha ^2\lambda _\alpha }{12}\right) + \partial _x \left( \displaystyle \frac{h_\alpha ^2 \lambda _\alpha \overline{u}_{\alpha }}{12} \right) +\displaystyle \frac{h_\alpha ^2 \lambda _\alpha }{12} \partial _x \overline{u}_{\alpha } \\ \qquad \quad = \Gamma _{\alpha +1/2}\bigg ( \displaystyle \frac{h_\alpha \lambda _{\alpha }}{12} + \displaystyle \frac{\overline{u}_{\alpha }-{\widetilde{u}}_{\alpha +1/2}}{2} \bigg ) -\Gamma _{\alpha -1/2}\bigg ( \displaystyle \frac{h_\alpha \lambda _{\alpha }}{12} - \displaystyle \frac{\overline{u}_{\alpha }-{\widetilde{u}}_{\alpha -1/2}}{2} \bigg ), \end{array}\right. \end{aligned}$$
(23)

for \(\alpha =1,\dots ,L\), where

$$\begin{aligned} \widetilde{u}_{\alpha +1/2} = \displaystyle \frac{\overline{u}_\alpha +\overline{u}_{\alpha +1}}{2} + \displaystyle \frac{h_\alpha \lambda _{\alpha } - h_{\alpha +1}\lambda _{\alpha +1}}{4}. \end{aligned}$$

This model verifies exactly a dissipative energy balance, stated by the following theorem.

Theorem 1

System (23) satisfies the dissipative energy balance

$$\begin{aligned} \partial _{t}\left( \displaystyle \sum _{\alpha =1}^L E_{\alpha }\right) \;+\; \partial _x\left( \displaystyle \sum _{\alpha =1}^L \overline{u}_{\alpha } \left( E_{\alpha } + gh_{\alpha }\displaystyle \frac{H}{2} +\displaystyle \frac{h_\alpha ^3 \lambda _{\alpha }^2}{12}\right) \right) \le 0, \end{aligned}$$

where

$$\begin{aligned} \smash E_{\alpha }:=\; h_\alpha \left( \displaystyle \frac{\overline{u}_{\alpha }^2+\overline{w}_{\alpha }^2}{2}+\displaystyle \frac{h_\alpha ^2 \lambda _{\alpha }^2}{24} + g\left( z_{b} + \frac{H}{2} \right) \right) . \end{aligned}$$

The proof can be seen as a particular case of the result stated in Theorem 2.

Remark 1

The hyperbolicity of layer-averaged models is still an open question. For the case of layerwise constant horizontal velocity, the hyperbolicity of the two-layer model (\(L=2\)) was proven in Aguillon et al. (2018). For \(L>2\) it is an open problem, up to our knowledge. Actually, following (Garres-Díaz et al. 2023, Remark 6), a loss of hyperbolicity could arise. Moreover, in Garres-Díaz and Bonaventura (2021) it is concluded that the hyperbolicity of these layer-averaged systems might be lost in the case of strong vertical profiles, that is, when large differences between the layer velocities (\(u_\alpha \)) and the averaged one (\({\overline{\overline{u}}}\)) appear. Notice that in this case the mass transfer terms (\(\Gamma _{\alpha +1/2}\)) may become large. Nevertheless, in these previous works (Garres-Díaz and Bonaventura 2021; Garres-Díaz et al. 2023), no loss of hyperbolicity was found in the numerical simulations performed.

Focusing now on the polynomial expansion of the velocity within each layer, the one-layer case corresponds to the so-called moment approach, giving as results the Shallow Water Moment models (see Kowalski and Torrilhon 2018). It was proven that only the case of linear velocity (system (23) with \(L=1\)) leads to a hyperbolic model, whereas the resulting system in the general case (polynomials \(u\in {\mathbb {P}}_{k>1}[z]\)) is not hyperbolic already for the one-layer case (see Koellermeier and Rominger 2020). Therefore, the same would hold for the multilayer case (\(L>1\) and \(u_\alpha \in {\mathbb {P}}_{k>1}[z]\)). This is also one of the reasons for not going to this general case in this work.

3 Non-hydrostatic layer-averaged systems with linear horizontal velocity: LIN-NH\(_k\) models

We consider now a non-hydrostatic pressure. Therefore, we must define the vertical profile for the vertical velocity and, consequently, for the non-hydrostatic pressure. Note that the incompressibility condition implies that inside each layer, the vertical velocity is a polynomial on z of degree \(d+1\), where d is the degree of the horizontal velocity (in this paper, we consider \(d=1\)). Thus, a family of models is presented, based on the degree of the polynomial employed to approximate the vertical momentum equation. We consider a polynomial of degree \(k \le d+1\), on z for the vertical velocity. We also consider that the pressure profile is a polynomial on z of degree \(k+1\), which becomes an essential hypothesis to obtain a system with an associated dissipative energy balance. In Fernández-Nieto et al. (2018), authors introduced a hierarchy of non-hydrostatic layer-averaged models for Euler equations for \(d=0\) and \(k\le 1\).

In the following subsections, firstly, the incompressibility condition within each layer is deduced. Secondly, three models are proposed, corresponding to different approximations of the vertical velocity and non-hydrostatic pressure counterparts. All of them satisfy a dissipative energy balance. We will detail the more complex model, where the vertical velocity is a layerwise quadratic polynomial according to the incompressibility condition, and therefore the non-hydrostatic pressure is a layerwise cubic function. Later, we see that if the vertical structure of the vertical velocity is simplified just for the vertical momentum equation, then the model degenerates to simpler models, but keeping still an analogous energy balance. This family of non-hydrostatic models will be denoted by Multilayer Horizontal Linear discretisation Non-Hydrostatic k model (from now on LIN-NH\(_k\)), where k is the degree of the polynomial approximating the vertical velocity in the vertical momentum conservation equation, that is, \(k=0,1,2\).

3.1 Averaged incompressibility condition

In the non-hydrostatic framework, we need some extra information or constraints to solve the resulting system, which now includes the degrees of freedom related to the non-hydrostatic pressure. Note that for each layer, there are three unknowns that define the non-hydrostatic pressure profile, namely \(q_{\alpha +1/2}\), \(\overline{q}_{\alpha }\) and \(\pi _\alpha \). Therefore, one would need three constraints at each layer.

On the one hand, two restrictions are associated to the relationship between the first and second order vertical derivative of the vertical and horizontal velocities. Concretely, in Sect. 2.1 the profile for the vertical velocity was obtained, where from the incompressibility inside each layer we got (12).

On the other hand, the jump condition (15a) reads

$$\begin{aligned} w_{\alpha +1/2}^+-w_{\alpha +1/2}^- = \left( u_{\alpha +1/2}^+-u_{\alpha +1/2}^-\right) \, \partial _x z_{\alpha +1/2}, \qquad \alpha =1,\dots , L-1. \end{aligned}$$
(24)

By substituting (7) and (13) in (24), we obtain

$$\begin{aligned}{} & {} \overline{w}_{\alpha +1}-\frac{h_{\alpha +1}\varphi _{\alpha +1}}{2} +\frac{h_{\alpha +1}^2\psi _{\alpha +1}}{12}- \overline{w}_\alpha -\frac{h_\alpha \varphi _\alpha }{2} -\frac{h_\alpha ^2\psi _\alpha }{12}\\{} & {} \quad =\bigg ( \overline{u}_{\alpha +1}-\frac{h_{\alpha +1} \lambda _{\alpha +1}}{2}- \overline{u}_\alpha -\frac{h_\alpha \lambda _\alpha }{2} \bigg ) \partial _x z_{\alpha +1/2}, \qquad \qquad \alpha =1,\dots ,L-1. \end{aligned}$$

To get the Lth constraint, let us integrate \(\nabla \cdot {\textbf{U}}_1=0\) between \(z_1\) and \(z_{1/2}\) (see Fernández-Nieto et al. 2018; Yamazaki et al. 2008). We obtain thanks to (9) applied to \(\alpha =1\)

$$\begin{aligned} \partial _x \overline{u}_{1} - \lambda _{1} \partial _x z_1 - \frac{h_1}{6} \partial _x \lambda _{1}+ \frac{ \overline{w}_1- w_{1/2}^+}{h_1/2}=0 \end{aligned}$$

Finally, the incompressibility conditions read

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \varphi _\alpha = -\partial _x \overline{u}_\alpha + \lambda _\alpha \partial _x z_\alpha , &{} \alpha =1,\dots , L. \\ \displaystyle \psi _\alpha = - \partial _x \lambda _\alpha , &{} \alpha =1,\dots , L, \\ \displaystyle \overline{w}_{\alpha +1}-\frac{h_{\alpha +1}\varphi _{\alpha +1}}{2} +\frac{h_{\alpha +1}^2\psi _{\alpha +1}}{12}- \overline{w}_\alpha -\frac{h_\alpha \varphi _\alpha }{2} -\frac{h_\alpha ^2\psi _\alpha }{12} \\ \displaystyle \qquad \qquad =\bigg ( \overline{u}_{\alpha +1}-\frac{h_{\alpha +1} \lambda _{\alpha +1}}{2}- \overline{u}_\alpha -\frac{h_\alpha \lambda _\alpha }{2} \bigg ) \partial _x z_{\alpha +1/2}, &{} \alpha =1,\dots ,L-1. \\ \displaystyle \partial _x \overline{u}_{1} - \lambda _{1} \partial _x z_1 - \frac{h_1}{6} \partial _x \lambda _{1}+ \frac{ \overline{w}_1- w_{1/2}^+}{h_1/2}=0. \end{array}\right. } \end{aligned}$$
(25)

where, in order to verify the kinematic condition (3), we set

$$\begin{aligned} w_{1/2}^+=w_b=\left( \overline{u}_1-\lambda _1 \frac{h_1}{2}\right) \partial _x z_b. \end{aligned}$$

3.2 LIN-NH\(_2\) model: non-hydrostatic model with \(w_\alpha \in {\mathbb {P}}_2[z]\)

In what follows we shall detail the first non-hydrostatic model that we propose here. It will be denoted by LIN-NH\(_2\) model. Its final formulation is (31) below with the subsequent notations. Later on, in Sect. 3.3 we shall introduce as well two extra simplified models, named LIN-NH\(_1\) and LIN-NH\(_0\) models.

Let us recall that, up to this point, we have evolution Eqs. (21) and (22) together with the restrictions (25) and the jump conditions (19) and (20).

In order to close the system, some extra equations are needed, which are obtained by successive integration on the vertical momentum conservation equation, as shown in what follows.

Let us first focus on the horizontal momentum Eqs. (21) and (22). In these equations, we compute, in the non-hydrostatic framework, the explicit pressure terms

$$\begin{aligned} \frac{1}{\rho }\displaystyle \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} \partial _x p_\alpha \, {\textrm{d}}z = g h_\alpha \partial _x (z_b+H) + \partial _x\left( h_\alpha \overline{q}_\alpha \right) - q_{{\alpha +1/2}}\partial _x z_{{\alpha +1/2}}+q_{{\alpha -1/2}}\partial _x z_{{\alpha -1/2}}, \end{aligned}$$

and

$$\begin{aligned}{} & {} \frac{1}{\rho h_\alpha } \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} (z-z_\alpha ) \partial _x p_\alpha \, {\textrm{d}}z =\frac{1}{10}\partial _x \left( h_\alpha \left[ \frac{(\delta q)_\alpha }{2} +\frac{\pi _\alpha }{3}\right] \right) +\overline{q}_\alpha \partial _x z_\alpha \\{} & {} \quad +\frac{\partial _x h_\alpha }{10}\left( h_\alpha \left[ \frac{(\delta q)_\alpha }{2} +\frac{\pi _\alpha }{3}\right] \right) - \frac{q_{\alpha +1/2} \partial _x z_{\alpha +1/2} +q_{\alpha -1/2} \partial _x z_{\alpha -1/2}}{2}. \end{aligned}$$

0

Let us focus now on the equations for the variables involved in the vertical velocity. To do so, we consider a basis in \({\mathbb {P}}_2[z]\) of test functions

$$\begin{aligned} \chi _\alpha (z) \in \left\{ 1,z-z_\alpha , \frac{(z-z_\alpha )^2}{2} - \displaystyle \frac{h^2_\alpha }{24}\right\} , \end{aligned}$$

and compute the averaged equations

$$\begin{aligned}{} & {} \partial _t\left( \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}}w_\alpha \chi _\alpha \,{\textrm{d}}z\right) + \partial _x\left( \int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}}u_\alpha w_\alpha \chi _\alpha \,{\textrm{d}}z\right) \nonumber \\{} & {} \qquad +\int _{z_{\alpha -1/2}}^{z_{\alpha +1/2}} \left( \chi _\alpha \partial _z q_\alpha - w_\alpha \partial _t\chi _\alpha -u_\alpha w_\alpha \partial _x\chi _\alpha -w^2_\alpha \partial _z\chi _\alpha \right) {\textrm{d}}z \nonumber \\{} & {} \quad = -\chi _{\alpha |_{z_{\alpha +1/2}}}{\widetilde{w}}_{\alpha +1/2}\Gamma _{{\alpha +1/2}} +\chi _{\alpha |_{z_{\alpha -1/2}}}{\widetilde{w}}_{\alpha -1/2}\Gamma _{{\alpha -1/2}}. \end{aligned}$$
(26)

For the sake of simplicity, we omit here the details of the computations. Let us introduce the following notations:

$$\begin{aligned} \Lambda _\alpha =\frac{h_\alpha \lambda _\alpha }{2\sqrt{3}}, \quad \Phi _\alpha =\frac{h_\alpha \varphi _\alpha }{2\sqrt{3}}, \quad \Psi _\alpha =\frac{h_\alpha ^2\psi _\alpha }{12\sqrt{5}}, \end{aligned}$$
(27)

obtaining hence the LIN-NH\(_2\) model, which reads

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}H + \partial _x\left( H\bar{{{\bar{u}}}}\right) = 0, \\ \partial _{t} (h_\alpha {\overline{u}}_{\alpha }) + \partial _x \bigg (h_\alpha \overline{u}_\alpha ^2 + h_\alpha \Lambda _\alpha ^2 + h_\alpha \overline{q}_\alpha \bigg ) + g h_\alpha \partial _x (z_b+H) \\ \qquad \qquad \, \, = q_{\alpha +1/2}\partial _x z_{\alpha +1/2}-q_{\alpha -1/2}\partial _xz_{\alpha -1/2}-{{\widetilde{u}}}_{\alpha +1/2}\Gamma _{\alpha +1/2}+{{\widetilde{u}}}_{\alpha -1/2}\Gamma _{\alpha -1/2}, \\ \partial _t \left( h_\alpha \Lambda _\alpha \right) + \partial _x \left( h_\alpha \Lambda _\alpha \overline{u}_\alpha + h_\alpha \displaystyle \frac{\sqrt{3}}{5} \left( \displaystyle \frac{q_{\alpha +1/2}-q_{\alpha -1/2}}{2}+\displaystyle \frac{\pi _\alpha }{3}\right) \right) +h_\alpha \Lambda _\alpha \partial _x \overline{u}_{\alpha } \\ \qquad \qquad \, \, +\displaystyle \frac{\sqrt{3}}{5} \left( \displaystyle \frac{q_{\alpha +1/2}-q_{\alpha -1/2}}{2}+\displaystyle \frac{\pi _\alpha }{3}\right) \partial _x h_\alpha - \sqrt{3} \left( q_{\alpha +1/2}\partial _x z_{\alpha +1/2}+ q_{\alpha -1/2}\partial _x z_{\alpha -1/2}\right) \\ \qquad \qquad \, \, + 2\sqrt{3}\ \overline{q}_\alpha \partial _x z_\alpha = \Gamma _{\alpha +1/2}\left( \Lambda _\alpha - \sqrt{3} ({\widetilde{u}}_{\alpha +1/2}-\overline{u}_{\alpha }) \right) \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, - \Gamma _{\alpha -1/2}\left( \Lambda _\alpha - \sqrt{3}(\overline{u}_{\alpha }-{\widetilde{u}}_{\alpha -1/2})\right) , \\ \partial _t \left( h_\alpha \overline{w}_\alpha \right) + \partial _x \left( h_\alpha \overline{u}_\alpha \overline{w}_\alpha + h_\alpha \Lambda _\alpha \Phi _\alpha \right) = -q_{\alpha +1/2}+q_{\alpha -1/2}-\widetilde{w}_{\alpha +1/2}\Gamma _{\alpha +1/2}\\ \qquad \qquad +\widetilde{w}_{\alpha -1/2}\Gamma _{\alpha -1/2}, \\ \partial _t\left( h_\alpha \Phi _\alpha \right) +\partial _x\left( h_\alpha \Phi _\alpha \overline{u}_\alpha + \displaystyle \frac{2\sqrt{5}}{5}h_\alpha \Lambda _\alpha \Psi _\alpha \right) + h_\alpha \Lambda _\alpha \partial _x \overline{w}_\alpha - 2\sqrt{3}\Psi _\alpha ^2 + \displaystyle \frac{2\sqrt{5}}{5}\Lambda _\alpha \Psi _\alpha \partial _x h_\alpha \\ \qquad \qquad \, \, + 2\sqrt{3}\left( \displaystyle \frac{q_{\alpha +1/2}+q_{\alpha -1/2}}{2} - \overline{q}_\alpha \right) = \Gamma _{{\alpha +1/2}}\left( \Phi _\alpha - \sqrt{3}(\widetilde{w}_{{\alpha +1/2}}-\overline{w}_\alpha )\right) \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad - \Gamma _{{\alpha -1/2}}\left( \Phi _\alpha - \sqrt{3}(\overline{w}_\alpha - \widetilde{w}_{{\alpha -1/2}})\right) , \\ \partial _t \left( h_\alpha \Psi _\alpha \right) + \partial _x \left( h_\alpha \Psi _\alpha \overline{u}_\alpha + \displaystyle \frac{2\sqrt{5}}{5} h_\alpha \Phi _\alpha \Lambda _\alpha \right) - \displaystyle \frac{6\sqrt{5}}{5} \Phi _\alpha \Lambda _\alpha \partial _x h_\alpha + 6\sqrt{3}\Phi _\alpha \Psi _\alpha \\ \qquad \qquad \, \, + \displaystyle \frac{2\sqrt{5}}{5}\bigl (q_{\alpha +1/2}-q_{\alpha -1/2}-\pi _\alpha \bigr ) = \Gamma _{\alpha +1/2}\left( 2\Psi _\alpha + \sqrt{15}\Phi _\alpha +\sqrt{5}(\overline{w}_{\alpha }-{\widetilde{w}}_{\alpha +1/2}) \right) \\ \qquad \qquad \qquad \qquad \quad \qquad \qquad \qquad - \Gamma _{\alpha -1/2}\left( 2\Psi _\alpha - \sqrt{15}\Phi _\alpha +\sqrt{5}(\overline{w}_{\alpha }-{\widetilde{w}}_{\alpha -1/2}) \right) , \end{array}\right. } \end{aligned}$$
(28)

for \(\alpha = 1,\dots ,L\), combined with the following constraints,

$$\begin{aligned} \left\{ \begin{array}{ll} h_\alpha \partial _x\overline{u}_\alpha +2\sqrt{3}\Phi _\alpha -2\sqrt{3}\Lambda _\alpha \partial _x z_\alpha =0, &{} \alpha =1,\dots , L,\\ \displaystyle \frac{2\sqrt{5}}{5}\Psi _\alpha +\displaystyle \frac{\sqrt{3}}{15}\left( h_\alpha \partial _x\Lambda _\alpha -\Lambda _\alpha \partial _xh_\alpha \right) =0, &{} \alpha =1,\dots , L, \\ \overline{w}_{\alpha +1}-\sqrt{3}\Phi _{\alpha +1}+\sqrt{5}\Psi _{\alpha +1} -\overline{w}_{\alpha }-\sqrt{3}\Phi _{\alpha }-\sqrt{5}\Psi _{\alpha }\\ \qquad \qquad \qquad =(\overline{u}_{\alpha +1}-\sqrt{3}\Lambda _{\alpha +1} - \overline{u}_{\alpha }-\sqrt{3}\Lambda _{\alpha })\partial _xz_{\alpha +1/2}&{} \alpha =1,\dots ,L-1, \\ \displaystyle \partial _x \overline{u}_{1} - \frac{2 \sqrt{3}}{h_1} \Lambda _{1} \partial _x z_1 - \frac{1}{\sqrt{3}} (\partial _x \Lambda _{1}-\Lambda _1 \partial _x h_1)+ \frac{ \overline{w}_1- w_{1/2}^+}{h_1/2}=0, \\ \end{array} \right. \end{aligned}$$
(29)

where

$$\begin{aligned} w_{1/2}^+=(\overline{u}_1-\sqrt{3}\, \Lambda _1) \partial _x z_b. \end{aligned}$$

In system (28) the velocities at the interfaces are given by

$$\begin{aligned} {\left\{ \begin{array}{ll} w_{\alpha \pm 1/2}^\mp =\overline{w}_\alpha \pm \sqrt{3}\Phi _\alpha +\sqrt{5}\Psi _\alpha , \\ u_{\alpha \pm 1/2}^\mp =\overline{u}_\alpha \pm \sqrt{3}\Lambda _\alpha , \\ \end{array}\right. } \end{aligned}$$
(30)

and, therefore,

$$\begin{aligned} \widetilde{u}_{\alpha +1/2} = \displaystyle \frac{\overline{u}_\alpha +\overline{u}_{\alpha +1}}{2} + \sqrt{3}\,\displaystyle \frac{\Lambda _{\alpha } - \Lambda _{\alpha +1}}{2} \end{aligned}$$

and

$$\begin{aligned} \widetilde{w}_{\alpha +1/2} = \displaystyle \frac{\overline{w}_\alpha +\overline{w}_{\alpha +1}}{2} + \sqrt{3}\,\displaystyle \frac{\Phi _{\alpha } - \Phi _{\alpha +1}}{2} + \sqrt{5}\,\displaystyle \frac{\Psi _{\alpha } + \Psi _{\alpha +1}}{2}. \end{aligned}$$

The system is thus composed of \(8\,L+1\) equations for \(8\, L+1\) unknowns,

$$\begin{aligned} \bigg (H, \{ \,\overline{u}_\alpha , \Lambda _\alpha , \overline{w}_\alpha ,\Phi _\alpha , \Psi _\alpha , \overline{q}_\alpha , q_{\alpha -1/2}, \pi _\alpha \}_{\alpha =1}^L \bigg ). \end{aligned}$$

Note that thanks to the vertical partition (4), using Eq. (18) for \(h_\alpha \) an explicit expression for \(\Gamma _{\alpha +1/2}\) is achieved, and then neither \(h_\alpha \) nor \(\Gamma _{\alpha +1/2}\) are unknowns anymore, unlike the total height H.

Finally, let us rewrite system (28) and constraints (29) in a compact way which will have the same structure for all models LIN-NH\(_k\):

figure b

where we introduced some notations, namely the vectors of unknowns

$$\begin{aligned} {\textbf{X}}_\alpha = \begin{pmatrix} \overline{u}_\alpha \\ \Lambda _\alpha \\ \overline{w}_\alpha \\ \Phi _\alpha \\ \Psi _\alpha \end{pmatrix}, \qquad {\textbf{Q}}_\alpha = \begin{pmatrix} \overline{q}_\alpha \\ q_{\alpha -1/2} \\ \pi _\alpha \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} {\textbf{F}}_\alpha= & {} \begin{pmatrix} \partial _x(h_\alpha \Lambda _\alpha ^2) \\ h_\alpha \Lambda _\alpha \partial _x\overline{u}_\alpha \\ \partial _x(h_\alpha \Lambda _\alpha \Phi _\alpha ) \\ \frac{2\sqrt{5}}{5}\partial _x(h_\alpha \Lambda _\alpha \Psi _\alpha ) -2\sqrt{3}\Psi _\alpha ^2 +h_\alpha \Lambda _\alpha \partial _x\overline{w}_\alpha +\frac{2\sqrt{5}}{5}\Lambda _\alpha \Psi _\alpha \partial _xh_\alpha \\ \frac{2\sqrt{5}}{5}\partial _x(h_\alpha \Lambda _\alpha \Phi _\alpha ) -\frac{6\sqrt{5}}{5}\Lambda _\alpha \Phi _\alpha \partial _xh_\alpha +6\sqrt{3}\Phi _\alpha \Psi _\alpha \\ \end{pmatrix}, \quad {\textbf{S}}_\alpha =\begin{pmatrix} -gh_\alpha \\ 0 \\ 0 \\ 0\\ 0\\ \end{pmatrix}, \\ {\textbf{G}}_\alpha ^{\pm }= & {} \begin{pmatrix} - \widetilde{u}_{\alpha \pm 1/2} \\ \Lambda _\alpha \pm \sqrt{3} (\overline{u}_{\alpha } -{\widetilde{u}}_{\alpha \pm 1/2}) \\ -\widetilde{w}_{\alpha \pm 1/2}\\ \Phi _\alpha \pm \sqrt{3}(\overline{w}_\alpha -\widetilde{w}_{\alpha \pm 1/2}) \\ 2\Psi _\alpha \pm \sqrt{15}\Phi _\alpha + \sqrt{5}(\overline{w}_{\alpha }-{\widetilde{w}}_{\alpha \pm 1/2}) \end{pmatrix} \end{aligned}$$

and the following differential operators, for \(\alpha \in \{1,\ldots ,L\}\)

$$\begin{aligned} \nabla _\textrm{NH}{\textbf{Q}}_\alpha =\begin{pmatrix} \partial _x(h_\alpha \overline{q}_\alpha )-\left( \delta \left( q\partial _xz \right) \right) _\alpha \\ \displaystyle \frac{\sqrt{3}}{5}\left[ \partial _x\left( h_\alpha \left( \displaystyle \frac{(\delta q)_\alpha }{2}+\displaystyle \frac{\pi _\alpha }{3}\right) \right) +10\overline{q}_\alpha \partial _xz_\alpha +\left( \displaystyle \frac{(\delta q)_\alpha }{2}+\displaystyle \frac{\pi _\alpha }{3}\right) \partial _xh_\alpha -10\widehat{(q\partial _xz)}_\alpha \right] \\ (\delta q)_\alpha \\ 2\sqrt{3}\left( {\widehat{q}}_\alpha -\overline{q}_\alpha \right) \\ \displaystyle \frac{2\sqrt{5}}{5}\left( {(\delta q)}_\alpha -\pi _\alpha \right) \end{pmatrix}. \end{aligned}$$

Then for \(\alpha \in \{2,\ldots ,L\}\) we define

$$\begin{aligned} \nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha =\begin{pmatrix} h_\alpha \partial _x\overline{u}_\alpha +2\sqrt{3}\Phi _\alpha -2\sqrt{3}\Lambda _\alpha \partial _x z_\alpha \\ \hline \overline{w}_\alpha -\overline{w}_{\alpha -1} -(\overline{u}_\alpha -\overline{u}_{\alpha -1})\partial _x z_{\alpha -1/2}-\sqrt{3}(\Phi _\alpha +\Phi _{\alpha -1})\\ +\displaystyle \frac{2\sqrt{5}}{5}(\Psi _\alpha -\Psi _{\alpha -1}) +\sqrt{3}(\Lambda _\alpha +\Lambda _{\alpha -1})\partial _xz_{\alpha -1/2}\\ +\displaystyle \frac{\sqrt{3}}{10}(\Lambda _\alpha \partial _xh_\alpha -h_\alpha \partial _x\Lambda _\alpha -\Lambda _{\alpha -1}\partial _xh_{\alpha -1}+h_{\alpha -1}\partial _x\Lambda _{\alpha -1}) \\ \hline \displaystyle \frac{1}{5}\left[ 2\sqrt{5}\Psi _\alpha +\displaystyle \frac{\sqrt{3}}{3}\left( h_\alpha \partial _x\Lambda _\alpha -\Lambda _\alpha \partial _xh_\alpha \right) \right] \end{pmatrix} \end{aligned}$$

and finally

$$\begin{aligned} \mathop {\nabla _\textrm{NH}}\cdot {\textbf{X}}_1 =\begin{pmatrix} h_1\partial _x\overline{u}_1+2\sqrt{3}\Phi _1 -2\sqrt{3}\Lambda _1\partial _x z_1 \\ \hline \overline{w}_1-\overline{u}_1\partial _xz_b+\sqrt{3}(\Lambda _1\partial _xz_b-\Phi _1) +\displaystyle \frac{\sqrt{3}}{10}(\Lambda _1\partial _xh_1-h_1\partial _x\Lambda _1) +\displaystyle \frac{2\sqrt{5}}{5}\Psi _1 \\ \hline \displaystyle \frac{2\sqrt{5}}{5}\Psi _1 +\displaystyle \frac{\sqrt{3}}{15}\left( h_1\partial _x\Lambda _1-\Lambda _1\partial _xh_1\right) \end{pmatrix}. \end{aligned}$$

These definitions of the NH-gradient and the NH-divergence operators satisfy the following duality relation,

$$\begin{aligned} \sum _{\alpha =1}^L{\textbf{X}}_\alpha \cdot (\nabla _\textrm{NH}{\textbf{Q}}_\alpha ) = -\sum _{\alpha =1}^L{\textbf{Q}}_\alpha \cdot (\nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha ) +\partial _x\left( \sum _{\alpha =1}^Lh_\alpha \left[ \overline{q}_\alpha \overline{u}_\alpha +\frac{\sqrt{3}}{5}\Lambda _\alpha \left( \frac{(\delta q)_\alpha }{2}+\frac{\pi _\alpha }{3}\right) \right] \right) .\nonumber \\ \end{aligned}$$
(32)

Remark 2

Notice that setting \(\Lambda _\alpha =0\), \(\Psi _\alpha =0\) and \(\pi _\alpha =0\), system (31) reduces to the \(LDNH_2(L)\) model described in Escalante-Sanchez et al. (2021) where the assumptions were: a layerwise-constant horizontal velocity, a layerwise-linear vertical velocity and a quadratic pressure.

An interesting property of such a system is that it satisfies a dissipative energy balance, as stated by the following theorem.

Theorem 2

The proposed LIN-NH\(_2\) model, defined by (31) satisfies the dissipative energy balance

$$\begin{aligned}{} & {} \partial _{t}\left( \displaystyle \sum _{\alpha =1}^L h_\alpha E_{\alpha }\right) + \partial _x\bigg (\displaystyle \sum _{\alpha =1}^L h_\alpha \bigg [ \overline{u}_{\alpha } \left( E_{\alpha } + g\displaystyle \frac{H}{2} + \Lambda _\alpha ^2 + \overline{q}_\alpha \right) + \Phi _\alpha \Lambda _\alpha \overline{w}_{\alpha } \\{} & {} \quad + \frac{2\sqrt{5}}{5}\Phi _\alpha \Psi _\alpha \Lambda _\alpha + \frac{\sqrt{3}}{5}\Lambda _\alpha \left( \frac{(\delta q)_\alpha }{2}+\displaystyle \frac{\pi _\alpha }{3}\right) \bigg ]\bigg ) \le 0, \end{aligned}$$

where

$$\begin{aligned} \smash E_{\alpha }:=\displaystyle \frac{|{\textbf{X}}_\alpha |^2}{2}+g\left( z_{b}+\frac{H}{2} \right) . \end{aligned}$$

Proof

The proof relies on algebraic relations. Let us multiply (31b) by \({\textbf{X}}_\alpha \). Notice that

$$\begin{aligned} {\textbf{X}}_\alpha \cdot \left[ \partial _t(h_\alpha {\textbf{X}}_\alpha )+\partial _x(h_\alpha {\textbf{X}}_\alpha \overline{u}_\alpha )\right] \overset{(32)}{=}&\partial _t\left( h_\alpha \frac{|{\textbf{X}}_\alpha |^2}{2}\right) +\partial _x\left( h_\alpha \frac{|{\textbf{X}}_\alpha |^2}{2}\overline{u}_\alpha \right) \\&\quad +\frac{|{\textbf{X}}_\alpha |^2}{2}\left( \Gamma _{{\alpha -1/2}}-\Gamma _{{\alpha +1/2}}\right) , \\ {\textbf{F}}_\alpha \cdot {\textbf{X}}_\alpha \overset{(31c)}{=}&\partial _x\left( h_\alpha \Lambda _\alpha \left[ \Lambda _\alpha \overline{u}_\alpha +\Phi _\alpha \overline{w}_\alpha +\frac{2\sqrt{5}}{5}\Phi _\alpha \Psi _\alpha \right] \right) , \end{aligned}$$

and

$$\begin{aligned} {\textbf{S}}_\alpha \cdot {\textbf{X}}_\alpha \partial _x\left( z_b+H\right)&= \partial _x\left( {\textbf{S}}_\alpha \cdot {\textbf{X}}\left( z_b+H\right) \right) + g\left( z_b+H\right) \partial _x\left( h_\alpha \overline{u}_{\alpha }\right) \\&= \partial _x\left( {\textbf{S}}_\alpha \cdot {\textbf{X}}\left( z_b+H\right) \right) + g\left( z_b+H\right) \left( \Gamma _{{\alpha -1/2}}-\Gamma _{{\alpha +1/2}}\right) \\&\quad - g\left( z_b+H\right) \partial _t h_\alpha , \end{aligned}$$

where

$$\begin{aligned} g\left( z_b+H\right) \partial _t h_\alpha= & {} g\left( z_b+\displaystyle \frac{H}{2}\right) \partial _t h_\alpha +g\displaystyle \frac{H}{2}\partial _t h_\alpha = \partial _t\left( h_\alpha \,g\left( z_b+\displaystyle \frac{H}{2}\right) \right) \\{} & {} \quad - \displaystyle \frac{g}{2}\left( h_\alpha \partial _t H-H\partial _t h_\alpha \right) . \end{aligned}$$

Given the expressions of interface velocities (30), we get

$$\begin{aligned}{} & {} \left( \Gamma _{\alpha +1/2}{\textbf{G}}_\alpha ^+-\Gamma _{\alpha -1/2}{\textbf{G}}_\alpha ^-\right) \cdot {\textbf{X}}_\alpha +\frac{|{\textbf{X}}_\alpha |^2}{2}(\Gamma _{\alpha +1/2}-\Gamma _{\alpha -1/2})\\{} & {} \quad =\Gamma _{\alpha +1/2}\left[ u_{\alpha +1/2}^-\left( \frac{u_{\alpha +1/2}^-}{2}-\widetilde{u}_{\alpha +1/2}\right) +w_{\alpha +1/2}^-\left( \frac{w_{\alpha +1/2}^-}{2}-\widetilde{w}_{\alpha +1/2}\right) \right] \\{} & {} \qquad -\Gamma _{\alpha -1/2}\left[ u_{\alpha -1/2}^+\left( \frac{u_{\alpha -1/2}^+}{2}-\widetilde{u}_{\alpha -1/2}\right) +w_{\alpha -1/2}^+\left( \frac{w_{\alpha -1/2}^+}{2}-\widetilde{w}_{\alpha -1/2}\right) \right] . \end{aligned}$$

Summing the last equality over all layers, we get

$$\begin{aligned}{} & {} \sum _{\alpha =1}^L\Gamma _{\alpha -1/2}\left[ \left( \widetilde{u}_{\alpha -1/2}-\frac{u_{\alpha -1/2}^-+u_{\alpha -1/2}^+}{2}\right) [u]_{\alpha -1/2}\right. \\{} & {} \quad \left. +\left( \widetilde{w}_{\alpha -1/2}-\frac{w_{\alpha -1/2}^-+w_{\alpha -1/2}^+}{2}\right) [w]_{\alpha -1/2}\right] =0 \end{aligned}$$

due to the definitionFootnote 1 of \(\widetilde{u}_{\alpha \pm 1/2}\), \(\widetilde{w}_{\alpha \pm 1/2}\) and

$$\begin{aligned} \sum _{\alpha =1}^L g\left( z_b+H\right) \left( \Gamma _{{\alpha -1/2}}-\Gamma _{{\alpha +1/2}}\right) = 0,\qquad \sum _{\alpha =1}^L\displaystyle \frac{g}{2}\left( h_\alpha \partial _t H-H\partial _t h_\alpha \right) = 0, \end{aligned}$$

which completes the proof. \(\square \)

Notice that thanks to the compact form (31) and the duality relation (32), the proof of Theorem 2 has been notably shortened. Let us also remark that in the case of smooth enough solutions, then the equality would hold in Theorem 2 instead of an inequality. This is also true for all the energy results in this work.

3.2.1 1-Layer model

In the 1-layer case, the model may be written in Boussinesq form by expressing all variables in terms of the averaged horizontal velocity and the fluid height as the only unknowns of the system. As we have said previously, this will result in a system of equations that contains third order derivatives in space and time. See for example, Fernández-Nieto et al. (2018), where it is shown that the LDNH\(_2\) model with 1 layer coincides with the Serre–Green–Naghdi model. More explicitly, the model proposed in this work for 1-layer case may be written as follows,

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _tH+\partial _x(H\overline{u})=0, \\ \partial _t(H\overline{u})+\partial _x(H\overline{u}^2)+\partial _x(H\Lambda ^2)+gH\partial _x(z_b+H) =-\partial _x(H\overline{q})-q_{1/2}\partial _x z_b, \\ \partial _t (H\Lambda )+ \partial _x (H\Lambda \overline{u}) +H\Lambda \partial _x \overline{u}= \displaystyle \frac{\sqrt{3}}{5}\partial _x\left( H \left( \displaystyle \frac{q_{1/2}}{2}-\displaystyle \frac{\pi }{3}\right) \right) - 2\sqrt{3}\ \overline{q}\partial _x \left( z_b+\displaystyle \frac{H}{2}\right) \\ \qquad +\displaystyle \frac{\sqrt{3}}{5} \left( \displaystyle \frac{q_{1/2}}{2}-\displaystyle \frac{\pi }{3}\right) \partial _x H + \sqrt{3}q_{1/2}\partial _xz_b,\\ \overline{w}=w_b-\displaystyle \frac{H}{2}\partial _x\overline{u}+\sqrt{3}\Lambda \partial _x\left( z_b+\displaystyle \frac{H}{3}\right) +\displaystyle \frac{H}{2\sqrt{3}}\partial _x\Lambda , \\ \Phi =-\displaystyle \frac{H\partial _x\overline{u}}{2\sqrt{3}}+\Lambda \partial _x\left( z_b+\displaystyle \frac{H}{2}\right) , \\ \Psi =\displaystyle \frac{1}{2\sqrt{15}}\left( \Lambda \partial _xH-H\partial _x\Lambda \right) , \\ q_{1/2}=H(\partial _t\overline{w}+\overline{u}\partial _x\overline{w})+\partial _x(H\Lambda \Phi ), \\ \overline{q}=\displaystyle \frac{q_{1/2}}{2}+\displaystyle \frac{1}{2\sqrt{3}}\left[ H(\partial _t\Phi +\overline{u}\partial _x\Phi ) + \displaystyle \frac{2\sqrt{5}}{5}\partial _x(H\Lambda \Psi ) +H\Lambda \partial _x \overline{w} - 2\sqrt{3}\Psi ^2 +\displaystyle \frac{2\sqrt{5}}{5}\Lambda \Psi \partial _x H\right] ,\\ \pi =-q_{1/2}+\displaystyle \frac{\sqrt{5}}{2}\left[ H(\partial _t \Psi + \overline{u}\partial _x \Psi ) + 6\sqrt{3}\Phi \Psi \right] + \partial _x(H\Phi \Lambda ) - 3\Phi \Lambda \partial _x H. \end{array}\right. } \end{aligned}$$

Note that by a subsequent substitution of the different unknowns of the system into the second and third equations, we easily obtain a system formed by three equations with the unknowns H, \(\overline{u}\) and \(\Lambda \), which includes terms of third order derivatives in space and time.

3.3 Simplified non-hydrostatic models

We propose now to obtain two simplified models in order to reduce the complexity of the previous one. The main objective is to reduce the number of unknowns related to the pressure and consequently the number of constraints. From a numerical point of view, this would be important to reduce the computational cost. For example, if a projection method is considered, it will be needed to solve a linear system for the pressure where the number of equations is proportional to the number of pressure variables and layers. Then, for the simplified models, we consider a more straightforward structure for the vertical velocity and, therefore, the non-hydrostatic pressure. We remark that it is essential that, to obtain models with an associated exact energy balance, we must always consider the incompressibility equation without any simplification on the vertical velocity profile.

We mention that among the two simplified models presented below, named LIN-NH\(_1\) and LIN-NH\(_0\), the one corresponding to a layerwise constant vertical velocity (LIN-NH\(_0\)) does not produce good results concerning the dispersive properties. However, we find interesting to show these results for the sake of completeness in the study, since it is natural to wonder whether it is a reasonable simplification or not. A possible reason for the poor results for that model could be that there should be a relation between the degrees of the polynomials approximating horizontal and vertical velocities. This fact would suggest that the degree of the polynomial approximation for the vertical velocity should be at least the one for the horizontal velocity, and it cannot be not be smaller.

The derivation of these simplified models can be obtained by following a similar approach as the one carried out in Sect. 3.2 for LIN-NH\(_2\) model. This results in a similar compact form (31). Hence analogous energy balances as in Theorem 2 are obtained. For the sake of brevity, we do not give here these proofs, which can be easily carried out following the analogous steps described in the proof of Theorem 2.

3.3.1 LIN-NH\(_1\) model: non-hydrostatic model with \(w_\alpha \in {\mathbb {P}}_1[z]\)

We consider first that the vertical velocity is a layerwise linear polynomial in z, \(w_\alpha \in {\mathbb {P}}_1[z]\) to approximate the vertical momentum equation, that is,

$$\begin{aligned} w_\alpha (z) = \overline{w}_\alpha + \varphi _\alpha \left( z-z_\alpha \right) \quad \text {for } z \in [z_{\alpha -1/2},z_{\alpha +1/2}]. \end{aligned}$$
(33)

Concerning the pressure, we consider a piecewise parabolic function, \(q_\alpha \in {\mathbb {P}}_2[z]\), given by

$$\begin{aligned} q_\alpha (z)=\displaystyle \frac{3\overline{q}_\alpha - \widehat{q}_\alpha }{2}+ (\delta q)_\alpha \,\frac{(z-z_\alpha )}{h_\alpha } + 6\left( \widehat{q}_\alpha -\overline{q}_\alpha \right) \displaystyle \frac{\left( z-z_\alpha \right) ^2}{h_\alpha ^2}, \quad \text {for }z \in [z_{\alpha -1/2},z_{\alpha +1/2}].\nonumber \\ \end{aligned}$$
(34)

Note that this pressure profile coincides with (14) by setting \(\pi _\alpha =(\delta q)_\alpha \). Then, the unknowns related to the non-hydrostatic pressure are \(\overline{q}_\alpha \), and \(q_{\alpha -1/2}\) for \(\alpha =1,\ldots ,L\). Recall that \(q_{L+1/2}\) is a given data, usually assumed to vanish at the surface.

The system thus comprises \(6\,L+1\) equations for \(6\, L+1\) unknowns,

$$\begin{aligned} \bigg (H, \{ \,\overline{u}_\alpha , \Lambda _\alpha , \overline{w}_\alpha ,\Phi _\alpha , \overline{q}_\alpha , q_{\alpha -1/2} \}_{\alpha =1}^L \bigg ). \end{aligned}$$

Analogously to what is done for the LIN-NH\(_2\) model, the LIN-NH\(_1\) model can be written in a compact form (31), where in this case

$$\begin{aligned} {\textbf{X}}_\alpha = \begin{pmatrix} \overline{u}_\alpha \\ \Lambda _\alpha \\ \overline{w}_\alpha \\ \Phi _\alpha \end{pmatrix}, \qquad {\textbf{Q}}_\alpha = \begin{pmatrix} \overline{q}_\alpha \\ q_{\alpha -1/2} \end{pmatrix}, \end{aligned}$$
(35)

with

$$\begin{aligned} {\textbf{F}}_\alpha =\begin{pmatrix} \partial _x(h_\alpha \Lambda _\alpha ^2) \\ h_\alpha \Lambda _\alpha \partial _x\overline{u}_\alpha \\ \partial _x(h_\alpha \Lambda _\alpha \Phi _\alpha ) \\ h_\alpha \Lambda _\alpha \partial _x\overline{w}_\alpha \end{pmatrix}, \quad {\textbf{G}}_\alpha ^{\pm } =\begin{pmatrix} - \widetilde{u}_{\alpha \pm 1/2} \\ \Lambda _\alpha \pm \sqrt{3} (\overline{u}_{\alpha } -{\widetilde{u}}_{\alpha \pm 1/2}) \\ -\widetilde{w}_{\alpha \pm 1/2}\\ \Phi _\alpha \pm \sqrt{3}(\overline{w}_\alpha -\widetilde{w}_{\alpha \pm 1/2}), \end{pmatrix},\quad {\textbf{S}}_\alpha =\begin{pmatrix} -gh_\alpha \\ 0 \\ 0 \\ 0 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{u}_{\alpha +1/2} = \displaystyle \frac{\overline{u}_\alpha +\overline{u}_{\alpha +1}}{2} + \sqrt{3}\,\displaystyle \frac{\Lambda _{\alpha } - \Lambda _{\alpha +1}}{2},\quad \text{ and }\quad \widetilde{w}_{\alpha +1/2} = \displaystyle \frac{\overline{w}_\alpha +\overline{w}_{\alpha +1}}{2} + \sqrt{3}\,\displaystyle \frac{\Phi _{\alpha } - \Phi _{\alpha +1}}{2}. \end{aligned}$$

The following NH-gradient operator read in this case, for \(\alpha \in \{1,\ldots ,L\}\),

$$\begin{aligned} \nabla _\textrm{NH}{\textbf{Q}}_\alpha =\begin{pmatrix} \partial _x(h_\alpha \overline{q}_\alpha )-\left( \delta \left( q\partial _xz \right) \right) _\alpha \\ \displaystyle \frac{\sqrt{3}}{6}\left[ \partial _x\left( h_\alpha (\delta q)_\alpha \right) +12\overline{q}_\alpha \partial _xz_\alpha +(\delta q)_\alpha \partial _xh_\alpha -12\widehat{(q\partial _xz)}_\alpha \right] \\ (\delta q)_\alpha \\ 2\sqrt{3}\left( {\widehat{q}}_\alpha -\overline{q}_\alpha \right) \end{pmatrix} \end{aligned}$$

and the NH-divergence operator, for \(\alpha \in \{2,\ldots ,L\}\)

$$\begin{aligned} \nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha =\begin{pmatrix} h_\alpha \partial _x\overline{u}_\alpha +2\sqrt{3}\Phi _\alpha -2\sqrt{3}\Lambda _\alpha \partial _x z_\alpha \\ \hline \overline{w}_\alpha -\overline{w}_{\alpha -1} -(\overline{u}_\alpha -\overline{u}_{\alpha -1})\partial _x z_{\alpha -1/2}-\sqrt{3}(\Phi _\alpha +\Phi _{\alpha -1}) \\ +\sqrt{3}(\Lambda _\alpha +\Lambda _{\alpha -1})\partial _xz_{\alpha -1/2}+\displaystyle \frac{\sqrt{3}}{6}(\Lambda _\alpha \partial _xh_\alpha -h_\alpha \partial _x\Lambda _\alpha -\Lambda _{\alpha -1}\partial _xh_{\alpha -1}+h_{\alpha -1}\partial _x\Lambda _{\alpha -1}) \end{pmatrix} \end{aligned}$$

and for \(\alpha =1\),

$$\begin{aligned} \mathop {\nabla _\textrm{NH}}\cdot {\textbf{X}}_1 =\begin{pmatrix} h_1\partial _x\overline{u}_1+2\sqrt{3}\Phi _1 -2\sqrt{3}\Lambda _1\partial _x z_1 \\ \hline \overline{w}_1-\overline{u}_1\partial _xz_b+\sqrt{3}(\Lambda _1\partial _xz_b-\Phi _1) +\displaystyle \frac{\sqrt{3}}{6}(\Lambda _1\partial _xh_1-h_1\partial _x\Lambda _1) \end{pmatrix}. \end{aligned}$$

These differential operators verify in this case the following duality relation,

$$\begin{aligned} \sum _{\alpha =1}^L{\textbf{X}}_\alpha \cdot (\nabla _\textrm{NH}{\textbf{Q}}_\alpha ) = -\sum _{\alpha =1}^L{\textbf{Q}}_\alpha \cdot (\nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha ) +\partial _x\left( \sum _{\alpha =1}^Lh_\alpha \left[ \overline{q}_\alpha \overline{u}_\alpha +\frac{\sqrt{3}}{6}\Lambda _\alpha (\delta q)_\alpha \right] \right) . \end{aligned}$$

This simplified system satisfies a dissipative energy balance, that coincides with the result stated at Theorem 2 by setting \(\Psi _\alpha =0\) and \(\pi _\alpha =(\delta q)_\alpha \). We obtain in this case the following result.

Theorem 3

The proposed LIN-NH\(_1\) model satisfies the dissipative energy balance

$$\begin{aligned}{} & {} \partial _{t}\left( \displaystyle \sum _{\alpha =1}^L h_\alpha E_{\alpha }\right) + \partial _x\bigg (\displaystyle \sum _{\alpha =1}^L h_\alpha \bigg [ \overline{u}_{\alpha } \left( E_{\alpha } + g\displaystyle \frac{H}{2} + \Lambda _\alpha ^2 + \overline{q}_\alpha \right) + \Phi _\alpha \Lambda _\alpha \overline{w}_{\alpha } + \frac{\sqrt{3}}{6}\Lambda _\alpha (\delta q)_\alpha \bigg ]\bigg )\\{} & {} \quad \le 0, \end{aligned}$$

where

$$\begin{aligned} \smash E_{\alpha }:=\displaystyle \frac{|{\textbf{X}}_\alpha |^2}{2}+g\left( z_{b}+\frac{H}{2} \right) . \end{aligned}$$

with \({\textbf{X}}_\alpha \) is defined by (35).

The proof is analogous to LIN-NH\(_2\) model.

3.3.2 LIN-NH\(_0\) model: non-hydrostatic model with \(w_\alpha \in {\mathbb {P}}_0[z]\)

Finally, we consider even a simpler case where a layerwise constant vertical velocity, \(w_\alpha \in {\mathbb {P}}_0[z]\), is assumed in the vertical momentum equation. Therefore, we have the structure

$$\begin{aligned} w_\alpha (z) = \overline{w}_\alpha \quad \text {for } z \in [z_{\alpha -1/2},z_{\alpha +1/2}], \end{aligned}$$
(36)

for the vertical velocity, and the pressure, which is linear \(q_\alpha \in {\mathbb {P}}_1[z]\), is given by

$$\begin{aligned} q_\alpha (z)=\widehat{q}_\alpha +(\delta q)_\alpha \,\frac{(z-z_\alpha )}{h_\alpha }, \quad \text {for }z \in [z_{\alpha -1/2},z_{\alpha +1/2}]. \end{aligned}$$
(37)

Now, we have only one pressure unknown by layer, \(q_{\alpha -1/2}\). Making such assumptions is equivalent to considering

$$\begin{aligned} \quad \overline{q}_\alpha = \widehat{q}_\alpha =\frac{q_{\alpha +1/2}+q_{\alpha -1/2}}{2} \quad \text {for }\alpha =1,\dots ,L. \end{aligned}$$
(38)

LIN-NH\(_0\) model can be written in a compact form (31), where in this case

$$\begin{aligned} {\textbf{X}}_\alpha = \begin{pmatrix} \overline{u}_\alpha \\ \Lambda _\alpha \\ \overline{w}_\alpha \end{pmatrix}, \qquad {\textbf{Q}}_\alpha = q_{\alpha -1/2}, \end{aligned}$$
(39)

with

$$\begin{aligned} {\textbf{F}}_\alpha =\begin{pmatrix} \partial _x(h_\alpha \Lambda _\alpha ^2) \\ h_\alpha \Lambda _\alpha \partial _x\overline{u}_\alpha \\ \partial _x(h_\alpha \Lambda _\alpha \Phi _\alpha ) \end{pmatrix}, \quad {\textbf{G}}_\alpha ^{\pm } =\begin{pmatrix} - \widetilde{u}_{\alpha \pm 1/2} \\ \Lambda _\alpha \pm \sqrt{3} (\overline{u}_{\alpha } -{\widetilde{u}}_{\alpha \pm 1/2}) \\ -\widetilde{w}_{\alpha \pm 1/2} \end{pmatrix},\quad {\textbf{S}}_\alpha =\begin{pmatrix} -gh_\alpha \\ 0 \\ 0 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \widetilde{u}_{\alpha +1/2} = \displaystyle \frac{\overline{u}_\alpha +\overline{u}_{\alpha +1}}{2} + \sqrt{3}\,\displaystyle \frac{\Lambda _{\alpha } - \Lambda _{\alpha +1}}{2},\qquad \text{ and }\qquad \widetilde{w}_{\alpha +1/2} = \displaystyle \frac{\overline{w}_\alpha +\overline{w}_{\alpha +1}}{2}, \end{aligned}$$

with the following NH-gradient operator for \(\alpha \in \{1,\ldots ,L\}\)

$$\begin{aligned} \nabla _\textrm{NH}{\textbf{Q}}_\alpha =\begin{pmatrix} \partial _x(h_\alpha \widehat{q}_\alpha )-\left( \delta \left( q\partial _xz \right) \right) _\alpha \\ \displaystyle \frac{\sqrt{3}}{6}\left[ \partial _x\left( h_\alpha (\delta q)_\alpha \right) -2(\delta q)_\alpha \partial _x h_\alpha \right] \\ (\delta q)_\alpha \end{pmatrix} \end{aligned}$$

and the NH-divergence operator, for \(\alpha \in \{2,\ldots ,L\}\)

$$\begin{aligned}{} & {} \nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha = \overline{w}_\alpha -\overline{w}_{\alpha -1} -(\overline{u}_\alpha -\overline{u}_{\alpha -1})\partial _x z_{\alpha -1/2}+\frac{1}{2}\left( h_\alpha \partial _x \overline{u}_\alpha +h_{\alpha -1} \partial _x \overline{u}_{\alpha -1}\right) \\{} & {} \quad -\frac{\sqrt{3}}{6}\left( 2\left( \Lambda _\alpha \partial _xh_\alpha -\Lambda _{\alpha -1}\partial _xh_{\alpha -1}\right) +h_\alpha \partial _x\Lambda _\alpha -h_{\alpha -1}\partial _x\Lambda _{\alpha -1}\right) \end{aligned}$$

and for \(\alpha =1\),

$$\begin{aligned} \mathop {\nabla _\textrm{NH}}\cdot {\textbf{X}}_1 = \overline{w}_1-\overline{u}_1\partial _xz_b+\frac{h_1}{2} \partial _x \overline{u}_1 -\frac{\sqrt{3}}{6}\left( h_1\partial _x\Lambda _1+2\Lambda _1\partial _xh_1\right) . \end{aligned}$$

These differential operators verify in this case the following duality relation,

$$\begin{aligned} \sum _{\alpha =1}^L{\textbf{X}}_\alpha \cdot (\nabla _\textrm{NH}{\textbf{Q}}_\alpha ) = -\sum _{\alpha =1}^L{\textbf{Q}}_\alpha \cdot (\nabla _\textrm{NH}\cdot {\textbf{X}}_\alpha ) +\partial _x\left( \sum _{\alpha =1}^Lh_\alpha \left[ \widehat{q}_\alpha \overline{u}_\alpha +\frac{\sqrt{3}}{6}\Lambda _\alpha (\delta q)_\alpha \right] \right) . \end{aligned}$$

This simplified system satisfies a dissipative energy balance, that coincides with the result stated at Theorem 2 by setting \(\Psi _\alpha =\Phi _\alpha =0\), \(\pi _\alpha =(\delta q)_\alpha \), \(\overline{q}_\alpha = \widehat{q}_\alpha \). Furthermore, in Tables 3 and 4 in Appendix A, the NH-divergence and NH-gradient operators for LIN-NH and LDNH models are summarized. In these tables, we also observe how these operators, in the case of simplified models, are obtained through appropriate simplifications in the operators associated to LIN-NH\(_2\) model.

4 Dispersion relations

In this section, we study the linear dispersion relations of the LIN-NH\(_k\) systems, following the approach used in Escalante et al. (2019), Lynett and Liu (2004b). In particular, we focus on the linear dispersion relations for the wave celerity, the group velocity and the linear shoaling. In other words, a formal study is performed for the PDE systems introduced previously, focusing on the propagation of dispersive waves.

To do so, a flat bottom is assumed as usual (\(z_b\) constant), and the governing equations are linearised around a steady-state solution. Then, a standard Stokes-type Fourier analysis is used to obtain the wave and group velocities. Finally, a shoaling analysis of the linearised equations is carried out.

4.1 Linear dispersion relation for the LIN-NH\(_2\) model

Let us begin with the LIN-NH\(_2\) model that is described by (28). Let us linearise the system around the steady state

$$\begin{aligned} z_b=-H_0=cst,\, u_0=\lambda _0=w_0=\varphi _0=\psi _0=0, \end{aligned}$$

and let us consider \(\eta =z_b+H\) the free-surface. We consider then the following asymptotic expansion

$$\begin{aligned} H = H_0 + \epsilon \eta ^{(1)} +O(\epsilon ^2), \end{aligned}$$
(40)

and for any variable \(\phi _\alpha \in \{\overline{u}_\alpha ,\lambda _\alpha ,\overline{w}_\alpha ,\varphi _\alpha ,\psi _\alpha \},\)

$$\begin{aligned} \phi _\alpha = \epsilon \phi _\alpha ^{(1)} + O(\epsilon ^2). \end{aligned}$$
(41)

For the sake of simplicity, we shall neglect in this section the superindex (1) and bars (\(\,\overline{\cdot }\,\)) so that the notation is less cumbersome. Using this linearisation in (28), we shall neglect \(O(\epsilon ^2)\) terms and keep the system at first order:

figure c

Remark that combining (42c), (42d), and (42i), we obtain

$$\begin{aligned} -(\delta q)_\alpha = \frac{\ell _\alpha ^2 H_0^2}{2}\partial _{tx} u_\alpha - \ell _\alpha H_0 \sum _{\beta =1}^{\alpha } \ell _\beta H_0 \partial _{tx} u_\beta - \frac{\ell _\alpha ^2H_0^2}{20} \partial _{xx} (\delta q)_\alpha - \frac{\ell _\alpha ^2H_0^2}{30} \partial _{xx} \pi _\alpha . \end{aligned}$$
(43)

Moreover, given that \(q_{L+1/2}=0\) and \((\delta q)_\alpha = q_{\alpha +1/2}- q_{\alpha -1/2}\) we have

$$\begin{aligned} q_{\alpha -1/2}= - \sum _{\beta =\alpha }^L (\delta q)_\beta . \end{aligned}$$

Let us consider now a plane-wave solution of the linearised system in the form

$$\begin{aligned} (\widehat{\eta },\widehat{u}_\alpha ,\widehat{\lambda }_\alpha ,\widehat{w}_\alpha ,\widehat{\varphi }_\alpha , \widehat{\delta q}_\alpha , \widehat{\pi }_\alpha )^T e^{i(kx-\omega t)}, \end{aligned}$$

where here the hat notation (\(\,\widehat{\cdot }\,\)) is new and is not related to (5b). Inserting the plane wave into (43) we get

$$\begin{aligned} -\left( 1+d_\alpha \right) \widehat{\delta q}_\alpha = \frac{\ell _\alpha ^2 H_0^2}{2}k\omega \widehat{u}_\alpha - \ell _\alpha H_0^2 k\omega \sum _{\beta =1}^\alpha \ell _\beta \widehat{u}_\beta ,\quad d_\alpha = \frac{\ell _\alpha ^{2} H_0^{2} k^{2}}{12\left( 1+\frac{\ell _\alpha ^{2} H_0^{2} k^{2}}{60}\right) }. \end{aligned}$$

Doing so in (42e) gives

$$\begin{aligned} \widehat{q}_\alpha = - \omega i \frac{\ell _\alpha ^2 H_0^2}{12} \widehat{\varphi }_\alpha + \widehat{q}_{\alpha +1/2}- \frac{\widehat{\delta q}_{\alpha +1}}{2} = - \omega i \frac{\ell _\alpha ^2 H_0^2}{12} \widehat{\varphi }_\alpha - \sum _{\beta =\alpha +1}^L \widehat{\delta q}_\beta - \frac{\widehat{\delta q}_\alpha }{2}. \end{aligned}$$

The same may be done in the other equations and we obtain, using the relation \(\widehat{\varphi }_\alpha = -i k \widehat{u}_\alpha \),

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega \widehat{\eta } = kH_0 \displaystyle \sum _{\alpha =1}^L \ell _\alpha \widehat{u}_\alpha , \\ \omega \widehat{u}_\alpha = k \widehat{q}_\alpha +gk \widehat{\eta }, \\ \left( 1+d_\alpha \right) \widehat{\delta q}_\alpha = -\frac{\ell _\alpha ^2 H_0^2}{2}k\omega \widehat{u}_\alpha + \ell _\alpha H_0^2 k\omega \sum _{\beta =1}^\alpha \ell _\beta \widehat{u}_\beta \\ \widehat{q}_\alpha = - \omega k \frac{\ell _\alpha ^2 H_0^2}{12} \widehat{u}_\alpha - \sum _{\beta =\alpha +1}^L \widehat{\delta q}_\beta - \frac{\widehat{\delta q}_\alpha }{2}. \end{array}\right. } \end{aligned}$$
(44)

Let us write the previous system under a linear system. First, consider the following vectors in \({\mathbb {R}}^L\)

$$\begin{aligned}{} & {} U=(\widehat{u}_1,\ldots ,\widehat{u}_L), \quad Q = (\widehat{q}_1,\ldots ,\widehat{ q}_L)^T, \quad \delta Q = (\widehat{\delta q}_1,\ldots ,\widehat{\delta q}_L)^T, \quad l = (\ell _1,\ldots ,\ell _L)^T, \\{} & {} \quad e = (1,\ldots ,1)^T, \end{aligned}$$

and the matrices of size \(L\times L\)

$$\begin{aligned} {\mathcal {L}}=\text {diag}(\ell _1,\ldots ,\ell _L), \quad {\mathcal {I}} = \text {diag} (1,\ldots ,1),\quad {\mathcal {I}}_d = \text {diag} (d_1,\ldots ,d_L),\\ {\mathcal {T}}=\left( \begin{array}{ccccc} \ell _1 &{}0 &{}0 &{}\ldots &{}0 \\ \ell _1 &{}\ell _2 &{} 0 &{}\ldots &{}0 \\ \ell _1 &{}\ell _2 &{} \ell _3 &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ \ell _1 &{}\ell _2 &{} \ell _3 &{} \ldots &{} \ell _L \\ \end{array} \right) , \quad {\mathcal {S}}=\left( \begin{array}{ccccc} 1 &{}1 &{}1 &{}\ldots &{}1 \\ 0 &{}1 &{} 1 &{}\ldots &{}1 \\ 0 &{}0 &{} 1 &{} \ldots &{} 1 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{}0 &{} 0 &{} \ldots &{} 1 \\ \end{array} \right) . \end{aligned}$$

Then (44) may be written as

$$\begin{aligned}{} & {} \omega ^2 U = k\omega Q + gk^2H_0 \langle l,U\rangle e,\\{} & {} Q=\left( \frac{1}{2} {\mathcal {I}}-{\mathcal {S}}\right) \delta Q - \omega k \displaystyle \frac{H_0^2}{12}{\mathcal {L}}^2 U,\\{} & {} \left( {\mathcal {I}}+{\mathcal {I}}_d\right) \delta Q = -k\omega \displaystyle \frac{H_0^2}{2} {\mathcal {L}}^2 U + k\omega {\mathcal {L}}{\mathcal {T}} U, \end{aligned}$$

where \(\langle \cdot , \cdot \rangle \) represents the scalar product in \({\mathbb {R}}^L\) and, performing a progressive substitution from bottom to top, we obtain

$$\begin{aligned} \omega ^2 {\mathcal {A}}_{2,L} U = g k^2 H_0 \langle l,U\rangle e, \end{aligned}$$

with

$$\begin{aligned} {\mathcal {A}}_{2,L}= k^2 H_0^2 \left( \displaystyle \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}\right) \left( {\mathcal {I}}+{\mathcal {I}}_d\right) ^{-1} \left( \frac{1}{2}{\mathcal {L}}^2-{\mathcal {L}}{\mathcal {T}}\right) +\left( {\mathcal {I}}+{\mathcal {I}}_d\right) . \end{aligned}$$

This means that, provided \({\mathcal {A}}_{2,L}\) is invertible,

$$\begin{aligned} \omega ^2 \langle e,U\rangle = g k^2 H_0 \langle l,U\rangle \langle {\mathcal {A}}_{2,L}^{-1} e, e\rangle . \end{aligned}$$

In the particular case \(\ell _\alpha =\displaystyle \frac{1}{L}\), \({\mathcal {A}}_{2,L}\) reduces to

$$\begin{aligned} {\mathcal {A}}_{2,L}= & {} \left( 1+d\right) {\mathcal {I}} + \frac{k^2 H_0^2}{L^2} \left( 1+d \right) ^{-1} \left( \displaystyle \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}\right) \left( \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}^T\right) ,\nonumber \\ d= & {} \displaystyle \frac{k^2H_0^2}{12\left( L^2+\displaystyle \frac{k^2H_0^2}{60}\right) }, \end{aligned}$$
(45)

and assuming \(\langle e,U\rangle \ne 0\) we get

$$\begin{aligned} \omega ^2 = g\frac{k^2H_0}{L} \langle {\mathcal {A}}_{2,L}^{-1} e, e\rangle , \end{aligned}$$

Therefore, the following dispersion relation for the wave celerity \(c:=\displaystyle \frac{\omega }{k}\) is obtained for LIN-NH\(_2\) model

$$\begin{aligned} \frac{c_{2,L}^2(k,H_0)}{gH_0} = \frac{\omega ^2}{gk^2H_0} = \frac{1}{L} \langle {\mathcal {A}}_{2,L}^{-1} e, e\rangle . \end{aligned}$$

4.2 Linear dispersion relation for the LIN-NH\(_1\) model

In the particular case of LIN-NH\(_1\), the equations that govern the system are those corresponding to (28) under the assumption of \((\delta q)_\alpha = \pi _\alpha ,\) as well as the restrictions (25).

Doing a linearisation as in (40) and (41) for \(\phi _\alpha \in \{\overline{u}_\alpha ,\lambda _\alpha ,\overline{w}_\alpha ,\varphi _\alpha \},\) keeping the first order terms and after inserting the plane wave solution

$$\begin{aligned} (\widehat{\eta },\widehat{u}_\alpha ,\widehat{\lambda }_\alpha ,\widehat{w}_\alpha ,\widehat{\varphi }_\alpha , \widehat{\delta q}_\alpha )^T e^{i(kx-\omega t)}, \end{aligned}$$

we obtain system (44) where, in this case, \(d_\alpha = \displaystyle \frac{\ell _\alpha ^{2} H_0^{2} k^{2}}{12}.\) That leads us, for the particular case \(\ell _\alpha = \displaystyle \frac{1}{L},\) to the following dispersion relation for the wave celerity \(c:=\displaystyle \frac{\omega }{k}:\)

$$\begin{aligned} \frac{c_{1,L}^2(k,H_0)}{gH_0} = \frac{\omega ^2}{gk^2H_0} = \frac{1}{L} \langle {\mathcal {A}}_{1,L}^{-1} e, e\rangle , \end{aligned}$$
(46)

where \({\mathcal {A}}_{1,L}\) is similar to (45), but with a change on the value of d,  more precisely:

$$\begin{aligned} {\mathcal {A}}_{1,L}= \left( 1+d\right) {\mathcal {I}} + \frac{k^2 H_0^2}{L^2} \left( 1+d \right) ^{-1} \left( \displaystyle \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}\right) \left( \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}^T\right) ,\quad d = \displaystyle \frac{k^2H_0^2}{12L^2}. \end{aligned}$$
(47)

4.3 Linear dispersion relation for the LIN-NH\(_0\) model

Remark that LIN-NH\(_0\) is quite similar to LIN-NH\(_1\) model, where some equations are removed and

$$\begin{aligned} q_\alpha =\displaystyle \frac{q_{\alpha +1/2}+ q_{\alpha -1/2}}{2}. \end{aligned}$$

This means that the linearisation (40) and (41) for \(\phi _\alpha \in \{\overline{u}_\alpha ,\lambda _\alpha ,\overline{w}_\alpha \}\), keeping the first order terms, will result in a reduced version of (42). Then, following a similar procedure as in the previous subsections, we get that a plane wave solution

$$\begin{aligned} (\widehat{\eta },\widehat{u}_\alpha ,\widehat{\lambda }_\alpha ,\widehat{w}_\alpha , \widehat{\delta q}_\alpha )^T e^{i(kx-\omega t)}, \end{aligned}$$

of this reduced linearised system should satisfy

$$\begin{aligned} {\left\{ \begin{array}{ll} \omega \widehat{\eta } = kH_0 \displaystyle \sum _{\alpha =1}^L \ell _\alpha \widehat{u}_\alpha , \\ \omega \widehat{u}_\alpha = k \widehat{q}_\alpha +gk \widehat{\eta }, \\ \left( 1+\displaystyle \frac{\ell _\alpha ^2 H_0^2 k^2}{12}\right) \widehat{\delta q}_\alpha = -\frac{\ell _\alpha ^2 H_0^2}{2}k\omega \widehat{u}_\alpha + \ell _\alpha H_0^2 k\omega \sum _{\beta =1}^\alpha \ell _\beta \widehat{u}_\beta \\ \widehat{q}_\alpha = - \sum _{\beta =\alpha }^L \widehat{\delta q}_\beta - \frac{\widehat{\delta q}_\alpha }{2}, \end{array}\right. } \end{aligned}$$

that is the same as (44) except for the term \( - \omega k \frac{\ell _\alpha ^2 H_0^2}{12} \widehat{u}_\alpha \), which is now missing in the last equation. As a consequence, for the particular case of \(\ell _\alpha = 1/L,\) we will obtain a matrix \({\mathcal {A}}_{0,L}\) similar to \({\mathcal {A}}_{1,L}\) in (47), but with the only difference that the last term \(\left( 1+d\right) {\mathcal {I}}\) is replaced by \({\mathcal {I}}.\) That is, the following dispersion relation for the wave celerity \(c:=\displaystyle \frac{\omega }{k}\) for LIN-NH\(_0\) model is satisfied:

$$\begin{aligned} \frac{c_{0,L}^2(kH_0)}{gH_0} = \frac{\omega ^2}{gk^2H_0} = \frac{1}{L} \langle {\mathcal {A}}_{0,L}^{-1} e, e\rangle , \end{aligned}$$

where

$$\begin{aligned} {\mathcal {A}}_{0,L}= {\mathcal {I}} + \frac{k^2 H_0^2}{L^2} \left( 1+\displaystyle \frac{k^2H_0^2}{12L^2} \right) ^{-1} \left( \displaystyle \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}\right) \left( \frac{1}{2}{\mathcal {I}}-{\mathcal {S}}^T\right) . \end{aligned}$$

4.4 Computation of the linear group velocity and the linear shoaling of dispersive systems

Let us introduce a general procedure that allows to compute the linear group velocity and shoaling for dispersive systems presented in this work.

Moreover, we provide a very general methodology that can be applied to compute the group velocity and the linear shoaling of any dispersive PDE system once the wave celerity \(c^2(k,H_0)\) of the system is known.

4.4.1 Group velocity

The group velocity \(c_g(k,H_0)\) is essentially computed by taking the derivative of the wave celerity c,  and is defined as

$$\begin{aligned} c_g = c + k \partial _k c. \end{aligned}$$

Let us express the ratio of the wave celerity of a given dispersive system and the shallow water celerity as a function of \(kH_0:\)

$$\begin{aligned} \displaystyle \frac{c^2(k,H_0)}{gH_0} = f(kH_0). \end{aligned}$$
(48)

For instance, for the LIN-NH\(_1\) model, f is given in (46) as:

$$\begin{aligned} f(kH_0) = \frac{1}{L} \langle {\mathcal {A}}_{1,L}^{-1} e, e\rangle . \end{aligned}$$

Therefore, the group velocity can be written as follows

$$\begin{aligned} c_g = \sqrt{gH_0} \Upsilon (kH_0),\quad \Upsilon (kH_0) = \displaystyle \frac{2f(kH_0)+kH_0 f'(kH_0)}{2 \sqrt{f(kH_0)}}, \end{aligned}$$
(49)

where \(f'\) means the derivative of the function f w.r.t. its argument.

4.4.2 Linear shoaling

The linear shoaling gradient \(\gamma \) is a non-dimensional quantity to measure the change in wave height in the presence of a bottom slope. It was firstly introduced in Madsen et al. (1991) and can be expressed as

$$\begin{aligned} \displaystyle \frac{\partial _x \eta }{\eta } = - \gamma \displaystyle \frac{\partial _x H_0}{H_0}. \end{aligned}$$

As usual, we will assume the dependency on the \(x-\)direction for \(H_0,\ \eta \) and the wave number k. On the contrary, we suppose that the frequency \(\omega \) does not depends on x,  and therefore \(\partial _x \omega = 0.\)

The linear shoaling gradient can be determined for a given dispersive PDE system by assuming the constancy of the energy flux

$$\begin{aligned} \partial _x{\left( \eta ^2c_g\right) }= 0, \end{aligned}$$

and, therefore,

$$\begin{aligned} \displaystyle \frac{\partial _x \eta }{\eta } = -\displaystyle \frac{1}{2}\displaystyle \frac{\partial _x c_g}{c_g}. \end{aligned}$$
(50)

Now, from (49), it yields

$$\begin{aligned} \displaystyle \frac{\partial _x c_g}{c_g} = \left( \displaystyle \frac{1}{2} + kH_0 \displaystyle \frac{\Upsilon '(kH_0)}{\Upsilon (kH_0)} \right) \displaystyle \frac{\partial _x H_0}{H_0} + kH_0 \displaystyle \frac{\Upsilon '(kH_0)}{\Upsilon (kH_0)} \displaystyle \frac{\partial _x k}{k}, \end{aligned}$$
(51)

where again \(\Upsilon '\) stands for the derivative of the function \(\Upsilon \) w.r.t. its argument.

Given the definition of the celerity \(c=\displaystyle \frac{\omega }{k}\) and the constancy of \(\omega \) with respect to x,  it follows that

$$\begin{aligned} \displaystyle \frac{\partial _x k}{k} = - \displaystyle \frac{\partial _x c}{c}, \end{aligned}$$

and from (48), we get

$$\begin{aligned} \displaystyle \frac{\partial _x k}{k} = - \displaystyle \frac{\partial _x c}{c} = - \left( \displaystyle \frac{1}{2} + kH_0 \displaystyle \frac{f'(kH_0)}{f(kH_0)}\right) \displaystyle \frac{\partial _x H_0}{H_0} - kH_0 \displaystyle \frac{f'(kH_0)}{f(kH_0)} \displaystyle \frac{\partial _x k}{k}. \end{aligned}$$

Therefore, from the above relation we can express \(\displaystyle \frac{\partial _x k}{k}\) as

$$\begin{aligned} \displaystyle \frac{\partial _x k}{k} = \left( \displaystyle \frac{1}{2} \displaystyle \frac{f(kH_0)}{f(kH_0) + kH_0 f'(kH_0)} - 1\right) \displaystyle \frac{\partial _x H_0}{H_0}. \end{aligned}$$
(52)

Finally, we can use (50), (51) and (52) to obtain the linear shoaling gradient of a given dispersive PDE system:

$$\begin{aligned} \displaystyle \frac{\partial _x \eta }{\eta } = - \gamma (kH_0) \displaystyle \frac{\partial _x H_0}{H_0},\quad \gamma (kH_0) = \displaystyle \frac{1}{4} \left( 1 + kH_0 \displaystyle \frac{\Upsilon '(kH_0)}{\Upsilon (kH_0)}\cdot \displaystyle \frac{f(kH_0)}{f(kH_0)+kH_0 f'(kH_0)}\right) . \end{aligned}$$
(53)

4.5 Comparison of the dispersion relations

Let us assess the different models in the framework of the Stokes linear theory, also called Airy theory, which establishes

$$\begin{aligned} \displaystyle \frac{c_{{\text {Airy}}}^2}{gH_0} = \frac{\tanh (kH_0)}{kH_0},\qquad \displaystyle \frac{c_{g,{\text {Airy}}}^2}{gH_0} = \displaystyle \frac{\left( 2kH_0 + \sinh (2kH_0)\right) ^2}{2kH_0(2\sinh (2kH_0) + \sinh (4kH_0))}, \end{aligned}$$

and

$$\begin{aligned} \gamma _{Airy} = kH_0 \tanh (kH_0)\displaystyle \frac{\left( 1-kH_0\tanh (kH_0)\right) \left( 1-\tanh ^2(kH_0)\right) }{\left( \tanh (kH_0) + kH_0 \left( 1-\tanh ^2(kH_0)\right) \right) ^2}. \end{aligned}$$

In what follows, we consider the relative dispersion error for the celerity and group celerity of the computed systems

$$\begin{aligned} \frac{c^2-c^2_{{\text {Airy}}}}{c^2_{{\text {Airy}}}},\qquad \frac{c_g^2-c^2_{g,{\text {Airy}}}}{c^2_{{\text {Airy}}}}, \end{aligned}$$

where c and \(c_g\) stands for the wave celerity and group velocity of a given dispersive system, respectively. Concerning the shoaling gradient, we directly compare, as usually done (see Escalante et al. 2019), the coefficients from the Airy theory, \(\gamma _{{\text {Airy}}},\) and the one given in the previous subsection \(\gamma \) for a given dispersive system.

For the sake of clarity, we have included in Appendix A a summary of all the models that are analysed in this section. In particular, we refer to Table 2 where the notation of the models, as well as the approximation spaces for the velocity and pressure fields, are summarized.

First, let us remark that it can be stated from Figs. 2 and 3 that the dispersion relations of the models studied here converge to the one given by the Stokes linear theory for the increasing number of layers L. The comparison between the relative dispersion error for the different models reveals that the new models LIN-NH\(_1\) and LIN-NH\(_2\) are the most accurate with bounded errors by \(1\ \%\) for an extensive range of \(kH_0\) up to 32. In the same way, we can state that the dispersion accuracy of the new model LIN-NH\(_0\) does not improve the one provided by LDNH\(_0\) or LDNH\(_2\), while the complexity of the model increases.

Fig. 2
figure 2

Comparison of the relative dispersion ratio and errors in logarithmic scale

Full size image
Fig. 3
figure 3

Comparison of the relative dispersion errors for the wave celerity for each model and different number of layers. Notice that the range for the y-axis in the subfigures corresponding with models LIN-NH\(_{1,2}\) is smaller to better distinguish the results

Full size image
Fig. 4
figure 4

Comparison between the relative dispersion errors for the wave celerity of different models, for a fixed number of layers \(L=1,2,3\)

Full size image
Fig. 5
figure 5

Comparison of the relative dispersion errors for the group velocity for each model and different number of layers. Notice that the range for the y-axis in the subfigures corresponding with models LIN-NH\(_{1,2}\) is smaller in order to better distinguish the results

Full size image
Fig. 6
figure 6

Comparison between the relative dispersion errors for the group velocity of different models, for a fixed number of layers \(L=1,2,3\)

Full size image
Fig. 7
figure 7

Comparison of the shoaling gradient of each model and different number of layers

Full size image
Fig. 8
figure 8

Comparison between the shoaling gradient of different models, for a fixed number of layers \(L=1,2,3\)

Full size image

In Fig. 4 we compare the relative dispersion errors for the new models with the corresponding one for LDNH\(_0\) and LDNH\(_2\) for different numbers of layers and ranges for \(kH_0.\) We can see again that both relative dispersion errors converge to 0 as the number of layers L increases. Nevertheless, the dispersion relation for the new model LIN-NH\(_2\) is now much better than that of LDNH\(_0\). Even for the simple case of one layer, the relative dispersion error is relatively small. Therefore, we can state that LIN-NH\(_2\) is an excellent choice in terms of dispersion accuracy. Despite the increased complexity of the model, it gives better results for large values of \(kH_0\) even for a small number of layers.

In the same way, we compare in Figs. 5 and 6 the group velocity, and in Figs. 7 and 8 the shoaling gradient for the different models considered in this work. We remark the great performance of the LIN-NH\(_1\) and LIN-NH\(_2\) models over LIN-NH\(_0\), LDNH\(_0\) and LDNH\(_2\).

In order to complete the dispersion study, we provide in Table 1 the minimum number of layers L that ensures errors smaller than \(5\ \%\) for the different dispersion relations and for different ranges of \(kH_0\in [0, 2^M]\)

$$\begin{aligned} 100\cdot \left\| \frac{c^2-c^2_{{\text {Airy}}}}{c^2_{{\text {Airy}}}}\right\| _{\infty }\le 5\ \%,\quad 100\cdot \left\| \frac{c_{g}^2-c^2_{g,Airy}}{c^2_{g,{\text {Airy}}}}\right\| _{\infty }\le 5\ \%,\quad 100\cdot \left\| \gamma -\gamma _{{\text {Airy}}}\right\| _{\infty }\le 5\ \%, \end{aligned}$$

where \(\left\| \cdot \right\| _{\infty }\) stands for the infinity norm

$$\begin{aligned} \left\| f \right\| _{\infty } = \displaystyle \max _{s\in [0,2^M]}\left| f(s)\right| . \end{aligned}$$

Note that we consider relative errors for the wave celerity and group velocity. However, absolute errors for the shoaling gradient are considered to avoid singularities when dividing by \(\gamma _{{\text {Airy}}}.\)

It can be highlighted the great performance of the model LIN-NH\(_2\) even for large ranges of the parameter \(kH_0.\) Despite the complexity of the presented models, the analysis of the dispersive properties for the LIN-NH\(_2\) model are outstanding. With no more than 2 layers, it can accurately simulate dispersive water waves of very high frequency.

Table 1 Minimum number of layers (L) that holds \(100\cdot \left\| \frac{f^2-f^2_{{\text {Airy}}}}{f^2_{{\text {Airy}}}}\right\| _{\infty }\le \ 5\%\), for \(f=c,c_g\) the wave celerity and the group velocity, respectively, and \(100\cdot \left\| \gamma -\gamma _{{\text {Airy}}}\right\| _{\infty }\le \ 5\%\) for the shoaling gradient
Full size table

5 Conclusions

A family of layer-averaged non-hydrostatic models for Euler equations with layerwise linear horizontal velocities, named LIN-NH\(_k\) with \(k=0,1,2\), has been presented. The derivation of these models follows from a layer-averaging procedure of the mass and momentum conservation equations, where normal jump conditions associated with the weak formulation of the problem are taken into account. In the notation LIN-NH\(_{k}\), the value k indicates the closure relation chosen for the vertical profile of the vertical velocity and pressure. Thus, k stands for the degree of the polynomial approximation of the vertical velocity, and \(k+1\) is the degree for the pressure.

Once the most complex model (LIN-NH\(_2\)) is derived, simplified LIN-NH\(_{0,1}\) models are obtained from simple assumptions upon the vertical profile of the vertical velocity, and therefore the pressure, just on the vertical momentum equation. It is important to remark that for the incompressibility constraints, the vertical profile of the velocity is not simplified for any model. For this very equation, the vertical velocity is always a layerwise parabolic polynomial. It is essential to prove a dissipative energy balance for all the proposed models. All the models are written in a compact form, which allows to prove the dissipative energy balance in a few lines. It is done by defining some non-hydrostatic differential operators, which satisfy a crucial duality relation. It is a remarkable issue, especially when designing numerical schemes for such models (see Escalante-Sanchez et al. 2021).

An analysis and a comparison of dispersion properties have been performed. In particular, we computed the linear dispersion, shoaling, and group velocity. Interestingly, models LIN-NH\(_{1}\) and LIN-NH\(_{2}\) provide accurate dispersion relations, although LIN-NH\(_1\) is a simpler model. Note that the latter model is computationally cheaper since it has 2L equations and unknowns less than LIN-NH\(_{2}\) model. LIN-NH\(_{1,2}\) models exhibit excellent dispersion properties for a wide range of wave numbers even for few layers. Then, these models can accurately reproduce dispersive water waves of very high frequency. We have also shown that LIN-NH\(_{1,2}\) models improve the results of the models introduced in Fernández-Nieto et al. (2018). On the other hand, the LIN-NH\(_{0}\) model, which relies on a layerwise constant vertical velocity assumption, provides poor results in the linear dispersion analysis. That would suggest that there should be a restriction between the degrees of the polynomial approximation assumed for the different variables. In particular, we could induce that the degree of the vertical velocity approximation should be greater than for the horizontal velocity. The extension to the Navier–Stokes case for a general rheology, accounting for the contribution of the deviatoric stress tensor, is addressed in the second part of this paper. In the future, it would be also interesting to propose efficient numerical schemes for LIN-NH\(_{1,2}\) models, following the strategy developed in Escalante-Sanchez et al. (2021) for LDNH models.