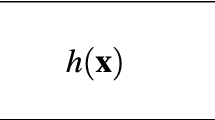Discrete octonion Fourier transform and the analysis of discrete 3-D data

Abstract

The purpose of this article is to further develop the theory of octonion Fourier transformations (OFT), but from a different perspective than before. It follows the earlier work by Błaszczyk and Snopek, where they proved a few essential properties of the OFT of real-valued functions of three continuous variables. The research described in this article applies to discrete transformations, i.e. discrete-space octonion Fourier transform (DSOFT) and discrete octonion Fourier transform (DOFT). The described results combine the theory of Fourier transform with the analysis of solutions for difference equations, using for this purpose previous research on algebra of quadruple-complex numbers. This hypercomplex generalization of the discrete Fourier transformation provides an excellent tool for the analysis of 3-D discrete linear time-invariant (LTI) systems and 3-D discrete data.

1 Introduction

Research in the field of signal and system processing is not only an analysis of the functions of a continuous variable (interpreted as time or space) and their representations in the frequency domain, but also in the field of discrete variables, which we naturally obtain as a result of the process of digitization (i.e. in connection with sampling of signals). As in the case of classical signal processing, so the discrete counterpart of this theory has so far mainly focused on signals with real and complex values, as well as their complex spectra. In recent years, however, more and more works have started to appear, which authors use in their research hypercomplex algebras, among others quaternions and octonions (Brackx et al. 2013; Hahn and Snopek 2016; Lian 2019; Snopek 2015; Wang et al. 2017). The area of applications is focused so far on the study of neural networks (Popa 2016, 2018), analysis of color and multispectral images (Ell et a. 2014; Gao and Lam 2014; Gomes et al. 2017; Grigoryan and Agaian 2018; Lazendić et al. 2018a, b; Sheng et al. 2018), as well as the biomedical signals processing (Delsuc 1988; Klco et al. 2017).

Octonions are defined as the 8-tuple of real numbers, i.e.

$$\begin{aligned} o = o_0 + o_1\mathbf{e}_1 + o_2\mathbf{e}_2 + o_3\mathbf{e}_3 + o_4\mathbf{e}_4 + o_5\mathbf{e}_5 + o_6\mathbf{e}_6 + o_7\mathbf{e}_7 \in \mathbb O, \quad o_0,\ldots ,o_7\in \mathbb R, \end{aligned}$$

where $\mathbf{e}_1,\ldots ,\mathbf{e}_7$ are seven different octonion imaginary units, each satisfying the property $\mathbf{e}_i^2=\mathbf{e}_i\cdot \mathbf{e}_i=-1$, $i=1,\ldots ,7$, and other octonion multiplication rules shown in Fig. 1. Octonions form a non-associative and a non-commutative algebra (Baez 2002).

In previous studies, we focused on discussing the properties of the octonion Fourier transform (OFT) of real-valued functions of three variables (and in the case of some properties, we extended this to octonion-valued functions) (Błaszczyk 2018, 2019, 2020; Błaszczyk and Snopek 2017). OFT is given by a formula

$$\begin{aligned} U_{\mathrm {OFT}}(f_1,f_2,f_3) = \int _\mathbb {R}\int _\mathbb {R}\int _\mathbb {R} u(x_1,x_2,x_3)\cdot \mathrm e^{-2\pi \mathbf {e}_1 f_1 x_1}\cdot \mathrm e^{-2\pi \mathbf {e}_2 f_2 x_2}\cdot \mathrm e^{-2\pi \mathbf {e}_4 f_3 x_3}\,\mathrm {d} x_1\mathrm {d} x_2\mathrm {d} x_3, \end{aligned}$$

(1)

where $\mathbf {e}_1$, $\mathbf {e}_2$ and $\mathbf {e}_4$ are three of the seven octonion imaginary units and the octonion exponential function is defined by the power series (Błaszczyk 2020), similarly as for the complex numbers and quaternions. In previous investigations (Błaszczyk 2020; Błaszczyk and Snopek 2017) it has been shown that (1) is well defined (i.e. the inverse transform theorem is valid) and some properties of the OFT, analogous to the properties of the complex and quaternion Fourier transform (e.g. Hermitian symmetry, shift theorem, Plancherel-Parseval theorems and derivative theorem) were also derived.

Fig. 1

Multiplication rules in octonion algebra

A major difficulty in these works was the lack of significant properties of octonion multiplication, i.e. commutativity and associativity. Non-commutativity is also encountered with Fourier transforms based on quaternion algebra and (in general) Clifford algebras (Brackx et al. 2013). In order to deal with these problems, we have defined the algebra of quadruple-complex numbers (based on the double-complex numbers introduced by Ell (1993); Kurman (1958)). Like octonions, we define the algebra of order 8 over the field of real numbers and each element of this algebra will be identified with the 8-tuple of real numbers (Błaszczyk 2019, 2020), i.e.

$$\begin{aligned} p = p_0+p_1\mathbf{E}_1+p_2\mathbf{E}_2+p_3\mathbf{E}_3+p_4\mathbf{E}_4+p_5\mathbf{E}_5+p_6\mathbf{E}_6+p_7\mathbf{E}_7\in \mathbb F, \quad p_0,\ldots ,p_7\in \mathbb R. \end{aligned}$$

Addition in $\mathbb F$ is defined in a classical way—element-wise, and multiplication (denoted as $\odot$) rules are shown in Fig. 2. We can see that imaginary units in $\mathbb F$ follow the analogous (although significantly different) rules as the octonion multiplication, i.e.

$$\begin{aligned} \mathbf{E}_1\odot \mathbf{E}_1=\mathbf{E}_2\odot \mathbf{E}_2=-\mathbf{E}_3\odot \mathbf{E}_3=\mathbf{E}_4\odot \mathbf{E}_4=-\mathbf{E}_5\odot \mathbf{E}_5=-\mathbf{E}_6\odot \mathbf{E}_6=\mathbf{E}_7\odot \mathbf{E}_7=-1. \end{aligned}$$

It is worth pointing out that, just as in the case of octonions, algebra $\mathbb F$ is generated by three imaginary units, i.e. $\mathbf{E}_1$, $\mathbf{E}_2$ and $\mathbf{E}_4$. Each other imaginary unit can be obtained by multiplying these three units, i.e. $\mathbf{E}_3=\mathbf{E}_1\odot \mathbf{E}_2$, $\mathbf{E}_5=\mathbf{E}_1\odot \mathbf{E}_4$, $\mathbf{E}_6=\mathbf{E}_2\odot \mathbf{E}_4$ and $\mathbf{E}_7=\mathbf{E}_1\odot \mathbf{E}_2\odot \mathbf{E}_4$. However, unlike octonions, the three basic imaginary units of algebra $\mathbb F$ are commutative. The multiplication in $\mathbb F$ is commutative and associative, however not every non-zero element of $\mathbb F$ has its inverse, which is a property common to Clifford algebras. This algebra has already appeared in the literature, in particular in Felsberg et al. (2001) (where it was denoted as hypercomplex algebra $\mathcal {H}_4$). By using operations in the quadruple algebra the notation of formulas for determining many OFT properties could be reduced to simple equations known from classical theory. We discussed that in detail in Błaszczyk (2019, 2020).

Fig. 2

Multiplication rules in $\mathbb F$

From the point of view of numerical calculations and practical applications, it is also important to develop discrete equivalents of the transformations under consideration and their properties. In the case of the classical Fourier transformation, this subject is well known, as in the case of quaternions (Bahri and Surahman 2013; Ell et a. 2014; Sangwine and Bihan 2005; Sangwine 1997). In the case of octonions, references to the analysis of 1- and 2-dimensional signals appear in the literature (Grigoryan and Agaian 2018), but there is still no definition of discrete octonion Fourier transform of 3-dimensional signals.

The paper is organized as follows. In Sect. 2 we recall previous results concerning the octonion Fourier transform and introduce some important properties. In Sect. 3 we focus on the discrete-time LTI systems, which leads to the definition of the discrete-space octonion Fourier transform. Its well-posedness and some of its properties are the main part of Sect. 4. Sections 5 and 6 are devoted to the discrete octonion Fourier transform—its definition, properties and implementation aspects. The implementation of the DOFT algorithm and the results of the first tests are also presented there. The paper is concluded in Sect. 7 with a short discussion of obtained results.

2 Octonion Fourier transform and some properties

As mentioned earlier, the OFT of the real-valued function $u:\mathbb R^3\rightarrow \mathbb R$ is given by the formula (1). In order for the integral (1) to exist, it is necessary for the function u to be at least integrable. However, in general, conditions of existence of the OFT are the same as for the classical (complex) Fourier transform (Błaszczyk 2020). Choice and order of imaginary units in the exponents is not accidental (see Błaszczyk and Snopek 2017). In our previous studies (see Błaszczyk and Snopek 2017), we proved the inverse formula (for continuous functions $u:\mathbb R^3\rightarrow \mathbb R$ such that both u and its OFT are integrable):

$$\begin{aligned} u(\mathbf{x}) = \int _{\mathbb R^3}\! U(\mathbf{f})\cdot e^{2\pi \mathbf{e}_4 f_3 x_3}\cdot e^{2\pi \mathbf{e}_2 f_2 x_2}\cdot e^{2\pi \mathbf{e}_1 f_1 x_1}\,\mathrm d\mathbf{f}, \end{aligned}$$

where $\mathbf{x}=(x_1,x_2,x_3)$, $\mathbf{f}=(f_1,f_2,f_3)$ and multiplication is performed from left to right. We have also proved some important features, among which there are those that will be useful in the analysis of discrete-variable signals (Błaszczyk 2020; Błaszczyk and Snopek 2017). Below, we quote their wording, assuming in each of these statements that the OFTs are well-defined and invertible. Let U be the OFT of the real-valued function u and let $u_{x_i}$ denote the partial derivative of u with respect to $x_i$.

Theorem 1

(Shift Theorem) Let $U^{\alpha }$, $U^{\beta }$ and $U^{\gamma }$ denote the OFTs of $u(x_1-\alpha ,x_2,x_3)$, $u(x_1,x_2-\beta ,x_3)$ and $u(x_1,x_2,x_3-\gamma )$, respectively. Then

$$\begin{aligned} U^{\alpha }(f_1,f_2,f_3)&= \cos (2\pi f_1\alpha )\; U(f_1,f_2,f_3) - \sin (2\pi f_1\alpha )\; U(f_1,-f_2,-f_3)\cdot \mathbf{e}_1, \\ U^{\beta }(f_1,f_2,f_3)&= \cos (2\pi f_2\beta )\; U(f_1,f_2,f_3) - \sin (2\pi f_2\beta )\; U(f_1,~ f_2,-f_3)\cdot \mathbf{e}_2, \\ U^{\gamma }(f_1,f_2,f_3)&= \cos (2\pi f_3\gamma )\; U(f_1,f_2,f_3) - \sin (2\pi f_3\gamma )\; U(f_1,~ f_2,~ f_3)\cdot \mathbf{e}_4. \end{aligned}$$

Theorem 2

Let $U^{\partial x_1}$, $U^{\partial x_2}$ and $U^{\partial x_3}$ denote the OFTs of $u_{x_1}$, $u_{x_2}$ and $u_{x_3}$, respectively. Then

$$\begin{aligned} U^{\partial x_1}(f_1,f_2,f_3)&= U(f_1, -f_2, -f_3)\cdot (2\pi f_1\mathbf{e}_1), \\ U^{\partial x_2}(f_1,f_2,f_3)&= U(f_1, ~f_2, -f_3)\cdot (2\pi f_2\mathbf{e}_2), \\ U^{\partial x_3}(f_1,f_2,f_3)&= U(f_1, ~f_2, ~f_3)\cdot (2\pi f_3\mathbf{e}_4). \end{aligned}$$

It seems that in the above form these statements are of little use. It is worth noting, however, that on the one hand we have a theorem on Hermitian symmetry (Błaszczyk and Snopek 2017), and on the other hand we can reformulate the given formulas using the operation $\odot$. Then these theorems take the form known from classical theory.

Corollary 1

Let $U^{\alpha }$, $U^{\beta }$ and $U^{\gamma }$ denote the OFTs of $u(x_1-\alpha ,x_2,x_3)$, $u(x_1,x_2-\beta ,x_3)$ and $u(x_1,x_2,x_3-\gamma )$, respectively. Then

$$\begin{aligned} U^{\alpha }(\mathbf{f}) = U(\mathbf{f})\odot \mathrm e^{-\mathbf{E}_1 2\pi f_1\alpha }, \quad U^{\beta }(\mathbf{f}) = U(\mathbf{f})\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2\beta }, \quad U^{\gamma }(\mathbf{f}) = U(\mathbf{f})\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3\gamma }. \end{aligned}$$

Corollary 2

Let $U^{\partial x_1}$, $U^{\partial x_2}$ and $U^{\partial x_3}$ denote the OFTs of $u_{x_1}$, $u_{x_2}$ and $u_{x_3}$, respectively. Then

$$\begin{aligned} U^{\partial x_1}(\mathbf{f}) = U(\mathbf{f})\odot (2\pi f_1\mathbf{E}_1), \quad U^{\partial x_2}(\mathbf{f}) = U(\mathbf{f})\odot (2\pi f_2\mathbf{E}_2), \quad U^{\partial x_3}(\mathbf{f}) = U(\mathbf{f})\odot (2\pi f_3\mathbf{E}_4). \end{aligned}$$

Remark 1

The claims of the Corollaries 1 and 2 should be understood in a specific way. We will show it on the example of the last formula in Corollary 2. The OFT of the real-valued function u can be expressed as

$$\begin{aligned} U = U_0 + U_1\mathbf{e}_1 + U_2\mathbf{e}_2 + U_3\mathbf{e}_3 + U_4\mathbf{e}_4 + U_5\mathbf{e}_5 + U_6\mathbf{e}_6 + U_7\mathbf{e}_7, \end{aligned}$$

where $U_0,\ldots ,U_7:\mathbb R^3\rightarrow \mathbb R$ are real-valued functions (we omit the argument of the function so as not to lose readability of the formula). Then

$$\begin{aligned} U\cdot \mathbf{e}_4 = -U_4 - U_5\mathbf{e}_1 - U_6\mathbf{e}_2 - U_7\mathbf{e}_3 + U_1\mathbf{e}_4 + U_2\mathbf{e}_5 + U_3\mathbf{e}_6 + U_4\mathbf{e}_7. \end{aligned}$$

On the other hand we can treat the octonion-valued function U as the 8-tuple of real-valued functions, which allows us to write this function as a $\mathbb F$-valued function:

$$\begin{aligned} U = U_0 + U_1\mathbf{E}_1 + U_2\mathbf{E}_2 + U_3\mathbf{E}_3 + U_4\mathbf{E}_4 + U_5\mathbf{E}_5 + U_6\mathbf{E}_6 + U_7\mathbf{E}_7. \end{aligned}$$

Then

$$\begin{aligned} U\odot \mathbf{E}_4 = -U_4 - U_5\mathbf{E}_1 - U_6\mathbf{E}_2 - U_7\mathbf{E}_3 + U_1\mathbf{E}_4 + U_2\mathbf{E}_5 + U_3\mathbf{E}_6 + U_4\mathbf{E}_7, \end{aligned}$$

which, again treating this expression as 8-tuple of real-valued functions, gives the statement of the Corollary. Other expressions should be understood analogously.

Proofs of these claims are based on direct calculations and we omit the details here. It should be remembered that the notation related to the operation $\odot$ serves only to increase the readability of performed operations and facilitate their interpretation. More importantly, it allows the direct use of the OFT for the analysis of LTI systems, which are described both by partial differential equations and difference equations (of three variables).

3 Discrete-time LTI systems

Consider linear time-invariant stationary system of three variables. We know from the classical signal and system theory that such systems are described by their impulse responses $h:\mathbb R^3\rightarrow \mathbb R$ (also sometimes called Green functions) and then the input-output relation of signals $u:\mathbb R^3\rightarrow \mathbb R$ and $v:\mathbb R^3\rightarrow \mathbb R$, respectively, is given by the formula:

$$\begin{aligned} v(\mathbf{x}) = \int _{\mathbb R^3} u(\mathbf{y})\cdot h(\mathbf{x}-\mathbf{y})\,\mathrm d\mathbf{y}= (u*h)(\mathbf{x}). \end{aligned}$$

The function at the output of the system is therefore a convolution of the function on the input with the impulse response, which is schematically presented in the block form as in Fig. 3.

Fig. 3

3-D-LTI system (block representation)

From the convolution-multiplication duality theorem for the classic Fourier transformation, it immediately follows that the following equality occurs:

$$\begin{aligned} \mathcal {F}_{\mathrm {CFT}}\left\{ v\right\} = \mathcal {F}_{\mathrm {CFT}}\left\{ u*h\right\} = \mathcal {F}_{\mathrm {CFT}}\left\{ h\right\} \cdot \mathcal {F}_{\mathrm {CFT}}\left\{ u\right\} , \end{aligned}$$

and function $H=\mathcal {F}_{\mathrm {CFT}}\left\{ h\right\}$ is called the frequency response of the system. In Błaszczyk (2019, 2020) we showed that the similar relation is valid also in case of octonion Fourier transform:

$$\begin{aligned} V(\mathbf{f}) = H_{\mathrm {OFT}}(\mathbf{f})\odot U(\mathbf{f}), \end{aligned}$$

where $H_{\mathrm {OFT}}$ is the octonion Fourier transform of the impuls response h (and therefore called the octonion frequency response) and we use the multiplication in the algebra of quadruple-complex numbers (in the sense described in Remark 1).

Thanks to these relations (and also Corollary 2), we can see that every linear partial differential equation with constant coefficients can be reduced to the algebraic equation (in the sense of multiplication in $\mathbb F$). In  Błaszczyk (2019, 2020) we presented a few examples showing the possibilities of using this notation.

Analogous reasoning can be performed for discrete-time systems. They are described mostly by difference equations, i.e. equations of the form:

$$\begin{aligned} \sum \limits _{i_1=0}^{M_1-1} \sum \limits _{i_2=0}^{M_2-1} \sum \limits _{i_3=0}^{M_3-1} a_\mathbf {i}\, u(\mathbf {n}-\mathbf {i}) = \sum \limits _{j_1=0}^{N_1-1} \sum \limits _{j_2=0}^{N_2-1} \sum \limits _{j_3=0}^{N_3-1} b_\mathbf {j}\, v(\mathbf {n}-\mathbf {j}),\qquad a_{(0,0,0)} \ne 0 \end{aligned}$$

where $u,v:\mathbb N^3\rightarrow \mathbb R$ are unknown sequences indexed by a 3-D discrete variable, $a_{\mathbf {i}},b_{\mathbf {j}}\in \mathbb R$, $\mathbf {n}=(n_1,n_2,n_3)$, $\mathbf {i}=(i_1,i_2,i_3)$ and $\mathbf {j}=(j_1,j_2,j_3)$. Using the octonion Fourier transform and Theorem 1, we can write this equality in a different form. However, only by composing Corollary 1 (and treating octonions as 8-tuples of real numbers, and therefore as elements of $\mathbb F$) we can reduce this relation to that which we know from classical theory:

$$\begin{aligned}&U(\mathbf{f}) \odot \left( \sum \limits _{i_1=0}^{M_1-1} \sum \limits _{i_2=0}^{M_2-1} \sum \limits _{i_3=0}^{M_3-1} a_\mathbf {i}\,\mathrm e^{-\mathbf{E}_1 2\pi f_1i_1}\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2i_2}\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3i_3}\right) \\&\qquad \qquad = V(\mathbf{f}) \odot \left( \sum \limits _{j_1=0}^{N_1-1} \sum \limits _{j_2=0}^{N_2-1} \sum \limits _{j_3=0}^{N_3-1} b_\mathbf {j}\,\mathrm e^{-\mathbf{E}_1 2\pi f_1j_1}\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2j_2}\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3j_3}\right) . \end{aligned}$$

It can be shown with direct calculations that

$$\begin{aligned} \mathrm e^{-\mathbf{E}_1 2\pi f_1i_1}\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2i_2}\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3i_3} = \mathrm e^{-\mathbf{e}_1 2\pi f_1i_1}\cdot \mathrm e^{-\mathbf{e}_2 2\pi f_2i_2}\cdot \mathrm e^{-\mathbf{e}_4 2\pi f_3i_3}, \end{aligned}$$

where the multiplication in the octonion algebra is performed from left to right. The above equality should be understood in the sense described in Remark 1, i.e. as the equality of 8-tuples of real numbers. Therefore we have

$$\begin{aligned}&U(\mathbf{f}) \odot \left( \sum \limits _{i_1=0}^{M_1-1} \sum \limits _{i_2=0}^{M_2-1} \sum \limits _{i_3=0}^{M_3-1} a_\mathbf {i}\,\mathrm e^{-\mathbf{E}_1 2\pi f_1i_1}\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2i_2}\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3i_3}\right) \\&\qquad \qquad = V(\mathbf{f}) \odot \left( \sum \limits _{j_1=0}^{N_1-1} \sum \limits _{j_2=0}^{N_2-1} \sum \limits _{j_3=0}^{N_3-1} b_\mathbf {j}\,\mathrm e^{-\mathbf{E}_1 2\pi f_1j_1}\odot \mathrm e^{-\mathbf{E}_2 2\pi f_2j_2}\odot \mathrm e^{-\mathbf{E}_4 2\pi f_3j_3}\right) , \end{aligned}$$

where expressions in brackets are some octonion counterparts to discrete Fourier transforms of vectors $\mathbf {a} = (a_{\mathbf {i}})$, $\mathbf {b} = (b_{\mathbf {j}})$ indexed by 3-D discrete variables.

4 Discrete-space octonion Fourier transform

The above considerations lead to the definition of the octonion counterpart of the discrete Fourier transform of real-valued sequences.

Definition 1

Let $\mathbf {a}:\mathbb N^3\rightarrow \mathbb R$ be a sequence indexed by a 3-D discrete variable and let $\mathbf {a} = (a_{\mathbf {i}})$, $\mathbf {i}=(i_1,i_2,i_3)$. Octonion Fourier transform of the sequence $\mathbf {a}$ is defined by the formula

$$\begin{aligned} A_{\mathrm {OFT}}(\mathbf{f}) = \sum \limits _{\mathbf {i}\in \mathbb N^3} a_{\mathbf {i}} \,\cdot \mathrm e^{-\mathbf{e}_1 2\pi f_1i_1}\cdot \mathrm e^{-\mathbf{e}_2 2\pi f_2i_2}\cdot \mathrm e^{-\mathbf{e}_4 2\pi f_3i_3},\quad \mathbf{f}=(f_1,f_2,f_3)\in \left( -\frac{1}{2},\frac{1}{2}\right) ^3, \end{aligned}$$

where multiplication is performed from left to right.

The above definition is a three-dimensional equivalent of the Fourier transformation of discrete time (discrete-time Fourier transform—DTFT), in relation to which the given formula can be abbreviatied as DSOFT (discrete-space octonion Fourier transform). Like its classic equivalent, DSOFT is a periodic function with relation to each variable, with a period of 1. Using the methods presented in the proof of the inverse theorem (Błaszczyk and Snopek 2017), the following formula can be derived for the inverse transform.

Theorem 3

Let $\mathbf {a}:\mathbb N^3\rightarrow \mathbb R$ be a sequence indexed by a 3-D discrete variable and let $\mathbf {a} = (a_{\mathbf {i}})$, $\mathbf {i}=(i_1,i_2,i_3)$, be square-summable. Then

$$\begin{aligned} a_{\mathbf {i}} = \int _{\left( -\frac{1}{2},\frac{1}{2}\right) ^3} A_{\mathrm {OFT}}(\mathbf{f})\cdot \mathrm e^{\mathbf{e}_4 2\pi f_3 i_3}\cdot \mathrm e^{\mathbf{e}_2 2\pi f_2 i_2}\cdot \mathrm e^{\mathbf{e}_1 2\pi f_1 i_1} \,\mathrm d\mathbf{f}, \end{aligned}$$

where multiplication is performed from left to right.

This theorem can be generalized to octonion-valued sequences, proving it with the same methods as in Błaszczyk (2018, 2020). From simple calculations the proof of the following theorem on the transformation of the rescaled function follows.

Theorem 4

Let $\mathbf {a}=(a_{\mathbf {i}}):\mathbb N^3\rightarrow \mathbb R$ and let A denote the DSOFT of $\mathbf {a}$. Let $k_1,k_2,k_3\in \mathbb N_+$, define $\mathbf {b}:\mathbb N^3\rightarrow \mathbb R$ by the formula:

$$\begin{aligned} b_{(i_1,i_2,i_3)} = {\left\{ \begin{array}{ll} a_{(i_1/k_1,i_2/k_2,i_3/k_3)} &{} \text {if }k_1|i_1\text {, }k_2|i_2\text { and }k_3|i_3{, } \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

and let B denote the DSOFT of $\mathbf {b}$. Then

$$\begin{aligned} B(f_1,f_2,f_3) = A(k_1f_1, k_2f_2, k_3f_3). \end{aligned}$$

Proof

From straightforward calculations we have that

$$\begin{aligned} B(f_1,f_2,f_3)&= \sum \limits _{\mathbf {i}\in \mathbb N^3} b_{\mathbf {i}} \,\cdot \mathrm e^{-\mathbf{e}_1 2\pi f_1i_1}\cdot \mathrm e^{-\mathbf{e}_2 2\pi f_2i_2}\cdot \mathrm e^{-\mathbf{e}_4 2\pi f_3i_3} \\&= \sum \limits _{\mathbf {j}\in \mathbb N^3} a_{\mathbf {j}} \,\cdot \mathrm e^{-\mathbf{e}_1 2\pi f_1k_1j_1}\cdot \mathrm e^{-\mathbf{e}_2 2\pi f_2k_2j_2}\cdot \mathrm e^{-\mathbf{e}_4 2\pi f_3k_3j_3} = A(k_1f_1, k_2f_2, k_3f_3), \end{aligned}$$

which concludes the proof. $\square$

It is worth noting that proofs of other properties of the octonion Fourier transformation (of functions of the continuous variable) proceeded in the same way as proofs of equivalents of these properties for the classic Fourier transform. Differences in statements of those theorems resulted only from the properties of multiplication of octonions, and, as a consequence, of operations on exponential functions in the kernel of transformation. Therefore, the equivalents of these properties for DSOFT will look the same, and their proofs will be very similar. We will therefore omit the details and quote only the statements.

Theorem 5

Let $\mathbf {a}=(a_{\mathbf {i}}):\mathbb N^3\rightarrow \mathbb R$ and let A denote the DSOFT of $\mathbf {a}$. Moreover, let $f_0\in \mathbb R$ and denote $\mathbf {a}^{\cos ,k}=(a_{\mathbf {i}})$, $a^{\cos ,k}_{\mathbf {i}} = a_{\mathbf {i}}\cdot \cos (2\pi f_0 i_k)$, and $A^{\cos ,k}$ as the DSOFT of $\mathbf {a}^{\cos ,k}$, $k=1,2,3$. Then

$$\begin{aligned} A^{\cos ,1}(f_1,f_2,f_3)&= \bigg (A(f_1+f_0,f_2,f_3) + A(f_1-f_0,f_2,f_3)\bigg )\cdot \frac{1}{2}, \\ A^{\cos ,2}(f_1,f_2,f_3)&= \bigg (A(f_1,f_2+f_0,f_3) + A(f_1,f_2-f_0,f_3)\bigg )\cdot \frac{1}{2}, \\ A^{\cos ,3}(f_1,f_2,f_3)&= \bigg (A(f_1,f_2,f_3+f_0) + A(f_1,f_2,f_3-f_0)\bigg )\cdot \frac{1}{2}. \end{aligned}$$

Theorem 6

Let $\mathbf {a}=(a_{\mathbf {i}}):\mathbb N^3\rightarrow \mathbb R$ and let A denote the DSOFT of $\mathbf {a}$. Moreover, let $f_0\in \mathbb R$ and denote $\mathbf {a}^{\sin ,k}=(a_{\mathbf {i}})$, $a^{\sin ,k}_{\mathbf {i}} = a_{\mathbf {i}}\cdot \sin (2\pi f_0 i_k)$, and $A^{\cos ,k}$ as the DSOFT of $\mathbf {a}^{\sin ,k}$, $k=1,2,3$. Then

$$\begin{aligned} A^{\sin ,1}(f_1,f_2,f_3)&= \big (A(f_1+f_0,-f_2,-f_3) - A(f_1-f_0,-f_2,-f_3)\bigg )\cdot \frac{\mathbf{e}_1}{2}, \\ A^{\sin ,2}(f_1,f_2,f_3)&= \bigg (A(f_1,f_2+f_0,-f_3) - A(f_1,f_2-f_0,-f_3)\bigg )\cdot \frac{\mathbf{e}_2}{2}, \\ A^{\sin ,3}(f_1,f_2,f_3)&= \bigg (A(f_1,f_2,f_3+f_0) - A(f_1,f_2,f_3-f_0)\bigg )\cdot \frac{\mathbf{e}_4}{2}. \end{aligned}$$

From the reasoning in the previous section, the shift theorem also immediately follows.

Theorem 7

Let $\mathbf {a}=(a_{\mathbf {i}}):\mathbb N^3\rightarrow \mathbb R$ and let A denote the DSOFT of $\mathbf {a}$. Moreover, let $\alpha ,\beta ,\gamma \in \mathbb Z$ and denote $\mathbf {a}^{\alpha } = (a^{\alpha }_{\mathbf {i}})$, $a^{\alpha }_{(i_1,i_2,i_3)} = a_{(i_1-\alpha ,i_2,i_3)}$, $\mathbf {a}^{\beta } = (a^{\beta }_{\mathbf {i}})$, $a^{\beta }_{(i_1,i_2,i_3)} = a_{(i_1,i_2-\beta ,i_3)}$, $\mathbf {a}^{\gamma } = (a^{\gamma }_{\mathbf {i}})$, $a^{\gamma }_{(i_1,i_2,i_3)} = a_{(i_1,i_2,i_3-\gamma )}$. Let $A^{\ell }$ denote the DSOFT of $\mathbf {a}^{\ell }$, where $\ell =\alpha ,\beta ,\gamma$. Then

$$\begin{aligned} A^{\alpha }(f_1,f_2,f_3)&= \cos (2\pi f_1\alpha ) A(f_1,f_2,f_3) - \sin (2\pi f_1\alpha ) A(f_1,-f_2,-f_3)\cdot \mathbf{e}_1 \\ A^{\beta }(f_1,f_2,f_3)&= \cos (2\pi f_2\beta ) A(f_1,f_2,f_3) - \sin (2\pi f_2\beta ) A(f_1,f_2,-f_3)\cdot \mathbf{e}_2 \\ A^{\gamma }(f_1,f_2,f_3)&= \cos (2\pi f_3\gamma ) A(f_1,f_2,f_3) - \sin (2\pi f_3\gamma ) A(f_1,f_2,f_3)\cdot \mathbf{e}_4 . \end{aligned}$$

As we mentioned earlier, deriving the DSOFT definition, it can be used to analyze discrete systems described by difference equations. It is also easy to see that these methods will be used in the analysis of finite difference schemes for partial differential equations. The theory considered so far mainly used classic Fourier transforms (discrete), which were applied to a variable interpreted as space (one- or two-dimensional), but by defining an octonion transformation we can try to transform the whole scheme, both for time and space.

5 Discrete octonion Fourier transform

In the previous section we considered signals (sequences) of infinite length. However, in practice, finite-length signals are usually found, which, as in the classical case, leads to the definition of discrete octonion Fourier transform. Similarly to the complex and quaternion case, the following definition has its basis in the discretization of the frequency domain in discrete-space octonion Fourier transform.

Definition 2

Let $\mathbf {a}:[N_1]\times [N_2]\times [N_3]\rightarrow \mathbb R$, $[N_i]=\{0,\ldots ,N_i-1\}$, be a finite-length sequence indexed by a 3-D discrete variable and let $\mathbf {a}=(a_{\mathbf {n}})$, $\mathbf {n}=(n_1,n_2,n_3)$. Discrete octonion Fourier transform (DOFT) $\mathbf {A}_{\mathrm {OFT}} = (A_{\mathrm {OFT},\mathbf {k}})$ of $\mathbf {a}$ is defined by the formula

$$\begin{aligned} A_{\mathrm {OFT},\mathbf {k}} = \sum \limits _{n_1=0}^{N_1-1} \sum \limits _{n_2=0}^{N_2-1} \sum \limits _{n_3=0}^{N_3-1} a_{(n_1,n_2,n_3)}\cdot \mathrm e^{-\mathbf{e}_1 2\pi k_1n_1/N_1}\cdot \mathrm e^{-\mathbf{e}_2 2\pi k_2n_2/N_2}\cdot \mathrm e^{-\mathbf{e}_4 2\pi k_3n_3/N_3}, \end{aligned}$$

(2)

where $\mathbf {k}=(k_1,k_2,k_3)\in [N_1]\times [N_2]\times [N_3]$ and multiplication is performed from left to right.

This is the direct octonion equivalent of the 3-D discrete Fourier transformation. The formula for inverse transformation is proved analogously to the corresponding formula for inverse OFT (Błaszczyk 2020). In particular, the following equality is used:

$$\begin{aligned} \frac{1}{N} \sum \limits _{k=0}^{N-1} \mathrm e^{-\mathbf{e}_i 2\pi kn/N}\cdot \mathrm e^{\mathbf{e}_i 2\pi km/N} = \delta _{m,n} = {\left\{ \begin{array}{ll} 1 &{} \text {if }m=n, \\ 0 &{} \text {if }m\ne n, \end{array}\right. } \end{aligned}$$

valid for every octonion imaginary unit $\mathbf{e}_i$, $i=1,\ldots ,7$. We omit the proof and only quote the statement of the inverse-transform theorem.

Theorem 8

Let $\mathbf {a}:[N_1]\times [N_2]\times [N_3]\rightarrow \mathbb R$, $[N_i]=\{0,\ldots ,N_i-1\}$, be a finite-length sequence indexed by a 3-D discrete variable and let $\mathbf {a}=(a_{\mathbf {n}})$, $\mathbf {n}=(n_1,n_2,n_3)$. If $\mathbf {A}_{\mathrm {OFT}} = (A_{\mathrm {OFT},\mathbf {k}})$ is the DOFT of $\mathbf {a}$, then

$$\begin{aligned} a_{\mathbf {n}} = \frac{1}{N_1N_2N_3} \sum \limits _{k_1=0}^{N_1-1} \sum \limits _{k_2=0}^{N_2-1} \sum \limits _{k_3=0}^{N_3-1} A_{\mathrm {OFT},(k_1,k_2,k_3)}\cdot \mathrm e^{\mathbf{e}_4 2\pi k_3n_3/N_3}\cdot \mathrm e^{\mathbf{e}_2 2\pi k_2n_2/N_2}\cdot \mathrm e^{\mathbf{e}_1 2\pi k_1n_1/N_1}, \end{aligned}$$

where multiplication is performed from left to right.

From a computational point of view, consideration should be given to the possibility of implementing a fast DOFT calculation version. In the quaternion case, various solutions to this problem have been proposed—direct implementation of the quaternion version of the Fast Fourier Transform algorithm (FFT) and the use of the complex (original) version of this algorithm. The latter option turned out to be better and less computationally demanding (Ell et a. 2014).

In the case of octonions, one can do the same. In Błaszczyk (2020) we proved that the octonion Fourier transformation of octonion-valued functions can be calculated using the classical Fourier transformation. This was formulated in the following statement (for proof see Błaszczyk 2020).

Theorem 9

Let $u:\mathbb R^3\rightarrow \mathbb O$ and $u = v_0 + v_1\mathbf{e}_2 + v_2\mathbf{e}_4 + v_3\mathbf{e}_2\cdot \mathbf{e}_4$, where $v_0,\ldots ,v_3:\mathbb R^3\rightarrow \mathbb C$. If $U_{\mathrm {OFT}}$ is the OFT of u, then

$$\begin{aligned} U_{\mathrm {OFT}}(f_1,f_2,f_3)&= V_0(~f_1,~f_2,~f_3)\; + V_1(-f_1,~f_2,-f_3)\cdot \mathbf{e}_2 \nonumber \\&\quad + V_2(-f_1,-f_2,~f_3)\cdot \mathbf{e}_4 + V_3(~f_1,-f_2,-f_3)\cdot \mathbf{e}_2\cdot \mathbf{e}_4, \end{aligned}$$

where $V_i$ is the OFT of $v_i$, $i=0,\ldots ,3$, and

$$\begin{aligned} V_i(f_1,f_2,f_3)&= \frac{1}{4}\big (\widehat{v_i}(f_1,f_2,f_3)\cdot (1-\mathbf{e}_3)+\widehat{v_i}(f_1,-f_2,f_3)\cdot (1+\mathbf{e}_3)\big )\cdot (1-\mathbf{e}_5) \nonumber \\&\qquad + \frac{1}{4}\big (\widehat{v_i}(f_1,f_2,-f_3)\cdot (1-\mathbf{e}_3)+\widehat{v_i}(f_1,-f_2,-f_3)\cdot (1+\mathbf{e}_3)\big )\cdot (1+\mathbf{e}_5), \end{aligned}$$

where $\widehat{v_i}$ is the classical (complex) Fourier transform of $v_i$, $i=0,\ldots ,3$.

It is important to notice that the field of complex numbers $\mathbb C$ used in the abovementioned theorem is the specific subfield of the octonion algebra, i.e. $\mathbb C=\{x_0 + x_1\mathbf{e}_1\in \mathbb O:x_0,x_1\in \mathbb R\}$. Consequently, only the imaginary units $\mathbf{e}_2$ and $\mathbf{e}_4$ appear in the thesis. Equivalent versions of the above theorem can be derived which take into account other pairs of imaginary units.

Analogous theorems for calculating the inverse transformation are also known (Błaszczyk 2020, Theorem 5 and Corollary 2). Due to the long formulation of the theorem, we omit it here. These claims remain true also for discrete transformations. The operation of changing the sign of a variable should be understood in the sense of modulo operations, as in the classic case—DOFT, just like DFT, can be treated as a periodic function.

Thanks to this, it is possible to use all the advantages of the FFT algorithm, with a small additional calculation effort—the octonion FFT algorithm for functions with octonion values requires the calculation of four transforms of different functions with complex values.

Tools for operations on hypercomplex numbers are available in many programming environments, including in MATLAB®. MATLAB® environment is one of the more popular tools supporting the work of engineers and packages expanding programming capabilities in this environment appear quite often. The qtfm package developed by the team of S. Sangwine and N. Le Bihan Sangwine and Bihan (2005) focuses on numerical calculations in quaternion algebra (not only basic arithmetic operations are available, but also highly developed tools for calculating quaternion Fourier transforms), but on the other hand, it also allows simple operations in octonion algebra. However, it lacks more advanced features that would give users the opportunity to calculate octonion Fourier transforms.

The qtfm package has been extended by, among others, five additional functions

• doft3 and idoft3 (forward and inverse DOFT using the direct formula),

• offt3 and iofft3 (forward and inverse DOFT using the FFT algorithm),

• fftreflection (symmetrical reflection of functions relative to the indicated axes).

The functions have been implemented using the qtfm package syntax. Octonions are entered in it, among others as

$$\begin{aligned} \texttt {octonion(r0, r1, r2, r3, r4, r5, r6, r7)}, \end{aligned}$$

where r0, ..., r7 are numbers or matrixes of numbers. It is also possible to automatically project real numbers, complex numbers and quaternions to the appropriate octonions, using the fact that they are created in the Cayley-Dickson construction (this is done using the available function cd).

The implementation of the forward and inverse discrete octonion Fourier transformation was performed in two ways—using the direct formula (2) and using Theorem 9, where first the classical (complex) Fourier transforms are calculated, and then they are combined in an appropriate manner. In the case of the direct algorithm, in order to avoid problems with multiplication of octonions, the matrix representation of multiplication presented in Tian (2000) was used. One of the important elements of the octonion FFT algorithm is the ability to symmetrically reflect functions with relation to the respective axes. This has been implemented in the fftreflection(X, A) function, where X is a mirrored function (matrix), and A is a vector that indicates which variables to reflect (e.g. [1,3] means that X is mirrored with respect to 1st and 3rd variable). It uses the convention that MATLAB® adopts with the FFT algorithm – zero frequencies always appear on the first coordinates of the matrix (in each dimension), and the discrete Fourier transform is a periodic function.

Implemented functions can be found in the GitHub repository:

https://github.com/blaszczykl/matlab-octonions and the code is also included in Appendix 1 (Listings 1–5). This is the original code developed by the author, however, it requires the qtfm package to work correctly (it is based on the syntax used in this package).

The correctness of implemented functions can be tested in two ways. First, it was checked whether applying the reverse transformation to the result of the forward transformation returned the original matrix. This check was done for both versions of the algorithm by generating random $N\times N\times N$ octonion matrices, where $N=4$ and each coordinate was generated from a uniform distribution over the interval [0, 1] (for details see Listing 7). In both cases, the maximum relative error did not exceed $2.2\cdot 10^{-11}\%$, which can be treated as a numerical approximation error.

It is worth noting the (expected) problem of calculation time for various quantities of N. In the case of the direct algorithm, the execution time is proportional to $N^6$, while for the FFT algorithm the time is proportional to $N^3 \log N$. This is not a surprising feature, it also applies to the classical DFT, however, due to operations on octonions, the time needed to perform calculations may be larger than in the case of the classical one. It can be seen that this issue is important.

To check whether an error was made when implementing the algorithm using Theorem 9 and whether it actually returns a discrete OFT, it was assumed that the direct algorithm returns the correct result and then it was compared with the result returned by the octonion FFT. In this case, the error did not exceed $1.5\cdot 10^{-12}\%$, which suggests that the implementation is correct.

6 Symmetry properties of the DOFT

As in the case of continuous OFT, most discrete classical equivalents of Fourier transform properties can be proved for discrete OFT. One of the first results for continuous OFT was to show the equivalent of Hermitian symmetry (Błaszczyk and Snopek 2017, Theorem 4.6). In the discrete case, the following theorem can be proved by repeating the reasoning presented in Błaszczyk and Snopek (2017).

Theorem 10

Let $\mathbf {a}:[N_1]\times [N_2]\times [N_3]\rightarrow \mathbb R$, $[N_i]=\{0,\ldots ,N_i-1\}$, be a finite-length sequence indexed by a 3-D discrete variable and let $\mathbf {a}=(a_{\mathbf {n}})$, $\mathbf {n}=(n_1,n_2,n_3)$. If $\mathbf {A}_{\mathrm {OFT}} = (A_{\mathrm {OFT},\mathbf {n}})$ is the DOFT of $\mathbf {a}$, then

$$\begin{aligned} A_{\mathrm {OFT},(m_1,n_2,n_3)}&= -\alpha _{7,5,3,1}(A_{\mathrm {OFT},(n_1,n_2,n_3)}), \\ A_{\mathrm {OFT},(n_1,m_2,n_3)}&= -\alpha _{7,6,3,2}(A_{\mathrm {OFT},(n_1,n_2,n_3)}), \\ A_{\mathrm {OFT},(n_1,n_2,m_3)}&= -\alpha _{7,6,5,4}(A_{\mathrm {OFT},(n_1,n_2,n_3)}), \end{aligned}$$

where $m_i = (-n_i \!\!\mod \; N_i)$, $\alpha _{i_1,\ldots ,i_4} = \alpha _{i_1}\circ \ldots \circ \alpha _{i_4}$ and $\alpha _{i}(o) = -\mathbf{e}_i\cdot o\cdot \mathbf{e}_i$.

It should be noted that the function $-\alpha _{i_1,\ldots ,i_4}$, introduced in Błaszczyk and Snopek (2017), changes the sign of four imaginary units of an octonion, i.e. $\mathbf{e}_{i_1}$, $\ldots$, $\mathbf{e}_{i_4}$. The above theorem should be interpreted so that the individual imaginary parts are even or odd with relation to the respective variables (in the sense of modulo operations).

The function $\alpha _{i_1,\ldots ,i_4}$ has also been implemented on the basis of the qtfm package as a function alpha(o, i1, i2, i3, i4) (see Listing 6), where o is the transformed octonion (or matrix of octonions) and i1, ..., i4 are four (different) indices of imaginary parts of o whose sign should be changed. The tests that could be performed thanks to this (presented in Listing 7) illustrate Theorem 10 and show that indeed DOFT of real-value matrices has the mentioned symmetry properties.

7 Discussion and conclusions

The results presented show that discrete Fourier transforms can be generalized to the case of higher order algebras (e.g. octonions). What’s more, using the properties of algebra of quadruple-complex numbers, this generalization can lead to a very similar form.

One could ask the question why it is worth working in two different algebras in parallel instead of just working in the algebra of quadruple-complex numbers $\mathbb F$. While going through calculations in $\mathbb F$ facilitates the interpretation of results, there are more and more papers in the literature devoted to the use of octonion algebra (Gao and Lam 2014; Grigoryan and Agaian 2018; Hahn and Snopek 2016; Klco et al. 2017; Lazendić et al. 2018a, b; Lian 2019; Popa 2016, 2018; Sheng et al. 2018; Snopek 2015; Wang et al. 2017). Therefore, it seems important to develop tools enabling work in this algebra as well.

The properties of discrete octonion Fourier transforms show that they can be used without difficulty for the analysis of difference equations, as well as for the analysis of finite difference schemes for differential equations. Detailed work in this area remains in the plans for further actions, as well as the further development of this theory.

MATLAB® files