1 Introduction

The very well-known secretary problem also has many modifications. Ferguson in [1] has made a review of the concepts of the best-choice problem (BCP) going back to the age of Kepler and the paper [2] by Cayley. Presman and Sonin in [3] considered so called no-information problem in which the appearing objects come from the rank distribution, that is, the objects are observable, the decision maker can rank them, and all permutations of the appearing objects are equally possible. The review paper [4] by Gilbert and Mosteller presented various models, also such that the exact value of the object is observable and the distribution of the object is known. (It is assumed to be a uniform distribution in the interval [0, 1].) Both ideas can be described as the optimal stopping of a Markov chain. In both, there is only one decision maker and there is no competition concept. The game theory approach to the secretary problem was introduced by Dynkin and presented in [5]. The problem of choosing the best object is later used to show the role of information that decision makers have. As in our work [6], we are dealing with a bilateral decision problem related to the observation of the Markov process by decision makers. The information provided to the players is based on the aggregation of the observation data. Acceptable strategies are moment of hold related to the available information. The payouts are the result of the selected state at the time that the decision maker stopped observing. As in the cited work, the decision makers are not identical (symmetric). They differ in access to information and have different rights to access the observed state, similar to the Stackelberg’s model (cf. [7]). The considered model is an extension of Dynkin’s game, but is also closely related to the models presented in the works [8,9,10], or [11]. Further, examples can be found in Mazalov’s book [12]. Another way to agree on acceptable behavior in stopping games has been proposed in the papers [13,14,15,16] (also cf. [17]).

1.1 Business Motivation

Consider a two companies A and B. Both of them are interested in buying a bundle of certain products on a commodity exchange. Company A is a large corporation and knows the actual value of the product on the market. In addition, it knows the previous values of the objects and can compare them. The problem of company B is that it does not have information about the actual value of the good. However, the owner of company B can compare the actual position of the good in the market with the previous observations. Both players want to choose the very best object overall without the possibility of recall. The number of objects is fixed and finite. A very good example can be described from the reliability position. Consider two buyers of the same item. Both want to buy the most reliable object. Buyer A has the ability to know the values of the reliability function derived by experts and quality controllers. The player B has no such contact and intelligence, so he must rely on his basic knowledge and the knowledge of the previous observation, i.e., he can judge whether the object is better or worse than the previous one. We can say that the buyers of the objects are two types: the first is a business, and the decision problem is preceded by unilateral consideration. The form of the optimal strategy in the decision problem is the inspiration for the mean-value formulation. Threshold strategies are crucial tools for optimal stopping problems. The simplest case related to the observation of a sequence of random variables can be found, e.g., in [18] or [19]. The bilateral extension of these models can be found in [20]. Two players, I and II, observe sequentially a known finite number (or a number having a geometric distribution) of independent and identically distributed random variables. They must choose the largest. Variables cannot be perfectly observed. When a random variable is sampled, the sampler is informed only whether it is greater or less than some level that he has specified. Each player can choose at most one observation. After the sampling, the players decide on acceptance or rejection of the observation. If both accept the same observation, Player I has priority. The class of adequate strategies and a gain function are constructed. In the finite case, the game has a solution in pure strategies. In the case of a geometric distribution, Player I has a pure equilibrium strategy, and Player II has either a pure equilibrium strategy or a mixture of two pure strategies. The game is symmetric, as the players are watching the same string to the same extent. Increasing opposing interests is possible by completely different preferences of the players. Evaluation of the same object by two decision makers can mean that players observe the different coordinates of the vector and formulate their expectations for their realization. When players’ aim is to achieve a minimum level of the observed rate, then the problem can be reduced to a game in which strategies are setting of just levels. Discussion of such issues can be found in the Sakaguchi’s works (e.g., [21]). However, in those tasks though, the information players are incomplete, lacking clear asymmetry players. The pay-offs of the players are function of the thresholds, and the perfect comparison of the observed variable with these defined levels is guaranteed. Asymmetric tools in measure of the observed r.v. are presented in [22]. However, for private random variables, these players with asymmetric tools applied to their same sequence are the subject of consideration in the paper.

1.2 Mathematical Formulation of the Problem

In fine-tuning the mathematical model, we will use the methods of optimal stopping of stochastic processes presented in the monograph by Chow et al. [23] (for Markov sequences in the monograph by Dynkin and Yushkievich in [24, 25]), and Dynkin’s game models with optimal stopping [5] of such sequences, similar to what is done in the works [10, 26].

Let \((\Omega ,{\mathcal {F}},{\textbf{P}})\) be rich enough probability space to define the random sequence \(\{X_n\}_{n=0}^N\), \(X_\cdot :\Omega \rightarrow {\mathbb {R}}\subset \Re \), \(N\in {\mathbb {N}}\cup \{\infty \}\). In general, one can define the filtration \({\mathcal {F}}_n=\sigma \{X_1,\cdots ,X_n\}\) and the set of stopping times \({\mathfrak {S}}\) with respect to the filtration. There are two observers (and, at the same time, decision makers) of the basic sequence defined by the mappings \(\{\varphi ^i_n\}\), \(i=1,2\), where \(\varphi ^i_n:\Re ^n\rightarrow \Re \), having his objectives defined by the payoff functions \(f^i:{\mathbb {R}}\rightarrow \Re \). In other words, the player I at the moment n observes \(\xi ^i_n=\varphi ^i_n(X_1,\cdots ,X_n)\). Let us denote \({\mathfrak {S}}^i\), \(i=1,2\), the sets of stopping times with respect to the filtration \({\mathcal {F}}^i_n=\sigma \{\xi ^i_1,\cdots ,\xi ^i_n\}\). The strategies of the players are stopping times \(\tau \in {\mathfrak {S}}^i\). Each player, on the basis of the observations available to him, is tasked with choosing the moment of accepting the state of the process based on the previous observations to maximize the expected payment.

$$\begin{aligned} {\hat{v}}^i=\sup _{\tau ^i\in {\mathfrak {S}}^i}{\mathbb {E}}f^i(X_{\tau ^i}). \end{aligned}$$
(1)

It can be used to reduce the initial problem to the task of optimal stopping of conditional expected values relative to its filtration (v. [25]). Let us calculate for every \(n\in {\mathbb {N}}\)

$$\begin{aligned} {\hat{f}}^i(\vec {\xi }^i_n)&={\textbf{E}}[f^i(X^i_n)\mid {\mathcal {F}}^i_n], \end{aligned}$$

where \(\vec {\xi }^i_n=(\xi ^i_1,\cdots ,\xi ^i_n)\). We have

$$\begin{aligned} {\hat{v}}^i&=\sup _{\tau ^i\in {\mathfrak {S}}^i}{\textbf{E}}{\hat{f}}^i(\vec {\xi }^i_{\tau ^i}). \end{aligned}$$

Let us assume that the observation processes \(\{\xi ^i_n\}_{n=0}^N\), \(i=1,2\), belong to Markov processes. In this case, the solution of the problem (1) can be obtained using the procedure described in [25, Ch.3] which is based on the Bellman-Jacobi equation. Denote \({\mathfrak {S}}_n=\{\tau \in {\mathfrak {S}}:\tau \geqslant n\}\). When we have two decision makers hunting for a convenient state of the process, they have the right to declare stopping at most twice. The second one is when the first hired state is assigned to the opponent. The natural set of strategies are \({\mathfrak {U}}^i=\{(\tau ^i,\{\sigma ^i_n\}_{n=0}^N):\tau ^i\in {\mathfrak {S}},\sigma ^i_n\in {\mathfrak {S}}_n^i\}\). The pay-off in the competitive case is defined in various ways. Following the discussion of the paper [10] for given \(\rho ^i\in {\mathfrak {U}}^i\), \(i=1,2\),

$$\begin{aligned} {\textbf{K}}_1\left( \rho ^1,\rho ^2\right)&={\textbf{E}}\Bigg [{\mathbb {I}}_{\{\tau ^1<\tau ^2\}}\left( {\hat{f}}^1\left( \xi ^1_{\tau ^1}\right) -{\hat{v}}^2 \left( \tau ^1,\xi ^2_{\sigma ^2_{\tau ^1}}\right) \right) \nonumber \\&\quad +{\mathbb {I}}_{\{\tau ^1=\tau ^2\}}\left[ p\Bigg ({\hat{f}}^1\left( \xi ^1_{\tau ^1}\right) -{\hat{v}}^2\left( \tau ^1,\xi ^2_{\sigma ^2_{\tau ^1}}\right) \right) \nonumber \\&\quad +(1-p)\left( {\hat{v}}^1\left( \tau ^2,\xi ^1_{\sigma ^1_{\tau ^2}}\right) -{\hat{f}}^2\left( \xi ^2_{\tau ^2}\right) \right) \Bigg ]\nonumber \\&\quad +{\mathbb {I}}_{\{\tau ^1>\tau ^2\}}\left( {\hat{v}}^1\left( \tau ^2,\xi ^1_{\sigma ^1_{\tau ^2}}\right) -{\hat{f}}^2\left( \xi ^2_{\tau ^2}\right) \right) \Bigg ], \end{aligned}$$
(2)

where \({\mathbb {I}}_A\) is the characteristic function of A and

$$\begin{aligned} {\hat{v}}^i(n,\xi ^i_n)=\sup _{\tau ^i\in {\mathfrak {S}}^i_n}{\textbf{E}}{\hat{f}}^i(\vec {\xi }^i_{\tau ^i}), \end{aligned}$$

and \(0\leqslant p \leqslant 1\) is the priority parameter, i.e., the probability that the state will be assigned to Player I. The pair of strategies \(({\rho ^1}^\star ,{\rho ^2}^\star )\) is the solution to the problem if for every \(\rho ^i\in {\mathfrak {U}}^i\),

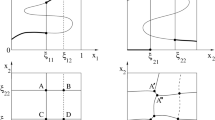
$$\begin{aligned} K_1({\rho ^1}^\star ,{\rho ^2}^\star )\geqslant K_1(\rho ^1,{\rho ^2}^\star ) \text { and } K_1({\rho ^1}^\star ,{\rho ^2}^\star )\geqslant K_1({\rho ^1}^\star ,\rho ^2). \end{aligned}$$

In practice, it is difficult to construct the solution and calculate the value of the problem in such general form. However, for some natural cases, each player can estimate his final reward by calculating his potential reward (award) based on his knowledge (filtration). The idea of these simplifications is presented in the next sections (Fig. 1).

2 Formulation of the Game Related to BCP

2.1 The Description of the Model

Consider a game in which two players want to choose the best object overall. They observe N objects sequentially. They get a profit only if the player chooses the best object and the rival will not do it.Footnote 1 In other case, he does not get the award. At each moment players analyze the state in sequential order and declare his wish. The second player claims his decision first. If both players want to stop on the current object, the nature chooses beneficiary by a lottery. Suppose that

  1. 1

    The player I have no information, i.e., at any time prior to the decision, he observes only the relative ranks of the current objects and the behavior of player II.

  2. 2

    The player II has full information, i.e., he observes sequentially \(X_1,\cdots ,X_N\) i.i.d., sees its value, and also can calculate the rank of the current object, and he presents the decision as soon as the observation is taken that player I knows it before making his own.

  3. 3

    A player who accomplishes his goal (chooses the moment when the process reaches its global maximum) gets a payout of 1. If his pick is unsuccessful, he incurs a \( -1\) penalty. Otherwise, he ends the game with a payout of 0.

To be more specific, let us denote by \(Y_n\) the relative rank of the n-th observation

$$\begin{aligned} Y_n = \# \lbrace 1 \leqslant i \leqslant n: X_i \leqslant X_n \rbrace . \end{aligned}$$
(3)

Player II filtration is \({\mathcal {F}}^{(1)}_n=\sigma (X_1,\cdots ,X_n)\) and for Player I it is \({\mathcal {F}}^{(2)}_n=\sigma (Y_1,\cdots ,Y_n)\). Note that \({\mathcal {F}}^{(2)}_n \subset {\mathcal {F}}^{(1)}_n\) for every n. Denote by \({\mathcal {T}}_1\) a set of all stopping times with respect to family \(\lbrace {\mathcal {F}}_{n} \rbrace _{n=1}^{N}\). Let \({\mathcal {T}}_{1}^{0}\) denote a set of all stopping times \(\tau \in {\mathcal {T}}_1\) such that \(X_{n} = \max \lbrace X_{1},\cdots ,X_{n} \rbrace \) on \(\lbrace \tau = n \rbrace \), \(n=1,\cdots ,N\), and \({\mathcal {T}}_{1,n}=\{\tau \in {\mathcal {T}}_1:\tau \geqslant n\}\). Define the moments where the greatest observations appear, that is, \(\tau _{1}=1\), \(\tau _{k}= \inf \lbrace n: \tau _{k-1} \leqslant n \leqslant N, X_{n} = \max \lbrace X_{1},\cdots ,X_{n} \rbrace \rbrace \) for \(k=1,\cdots ,N\). We observe the sequence \(\tau _1, \tau _2,\cdots \in {\mathcal {T}}_{1}^{0}\). Now let us consider the following chain,

$$\begin{aligned} Z_{k}= (\tau _k, X_{\tau _k}) \text { on } \lbrace \tau _k < N+1 \rbrace , Z_{k}=(\tau _{N+1},\partial ), \end{aligned}$$

where \(\partial \) is a special absorbing state. It is easy to see that \(\lbrace Z_{k} \rbrace _{k=1}^{N+1}\) is a Markov chain with transition probabilities (cf. [27])

$$\begin{aligned} p((n,x),(m,B)) = x^{m-n-1}\int _{B}{\text {d}}y, \text { for}\ m>n, x\in (0,1], \end{aligned}$$

and, 0 otherwise, with \(B \subseteq (x,1]\). It means that the density function

$$\begin{aligned} p((n,x),(m,{\text {d}}y)):=p((n,x),(m,(y,y+{\text {d}}y))) = x^{m-n-1}{\text {d}}y, \end{aligned}$$
(4)

for \(m>n\), \(x,y\in (0,1]\), \(x\leqslant y\).

Fig. 1
figure 1

Boundaries of the strategies for \(N=10, p=0.25\). The shift for Player I is clearly visible. In this case \(n^*=4\) but \({\tilde{n}}=5\)

Full size image

The reward for Player II for stopping at the nth object of the value \(X_n=x\) is the following

$$\begin{aligned} s_{2,n}(x)=x^{N-n}, \end{aligned}$$
(5)

and for continuing observation and stopping on the next local maximum, taking into account (4), it is given by (cf. [4, 27])

$$\begin{aligned} c_{2,n}(x)=\sum _{k=n+1}^{N} \int _x^1s_{2,k}(y)p((n,x),(k,{\text {d}}y)) = \sum _{k=n+1}^{N}\dfrac{x^{k-n-1}(1-x^{N-n})}{N-k+1}. \end{aligned}$$

Since the sequence of local maxima is increasing, then \(c_{2,n}(x) \leqslant s_{2,n}(x)\) for \( x \geqslant x_n\), where \(x_n\) is the only solution to the equation \(c_{2,n}(x) = s_{2,n}(x) \in (0,1]\). An explicit form of the equation is

$$\begin{aligned} \sum _{j=1}^{N-n}\frac{x^{-j}-1}{j}=1. \end{aligned}$$

Based on the above denotations and theory of optimal stopping, we have

$$\begin{aligned} u_{2,n}(x)=\sup _{\tau \in {\mathcal {T}}_{1,n}^{0}}{\textbf{E}}_{(n,x)}s_{2,\tau }(X_\tau )=\max \{s_{2,n}(x),{\textbf{T}}u_{2,n}(x)\}. \end{aligned}$$
(6)

Similarly, for the player I, consider a sequence of indicators \(\lbrace I_{n} \rbrace _{n=1}^{N}\), where \(I_{k}={\mathbb {I}}_{\{Y_k=1\}}\). Let us denote by \({\mathcal {G}}_{n} = \sigma (I_{1},\cdots ,I_{n})\) sequence of sigma fields generated by indicators, and let \({\mathcal {T}}_{2}\) be the set of all stopping moments \(\tau \) with respect to \(\sigma \) -fields \({\mathcal {G}}_{n}\), \(n=1,\cdots ,N\). Define a process \(\xi _t\) in the following way,

$$\begin{aligned} \xi _{t}=\inf \lbrace n\geqslant \xi _{t-1}: I_{n}=1 \rbrace \end{aligned}$$

with initial point \(\xi _{0}=1\). Calculate transition probabilities (cf. [24])

$$\begin{aligned} p_{n,m} = P(\xi _{k+1}=m\mid \xi _{k}=n). \end{aligned}$$
(7)

The first player’s reward for stopping on the nth candidate (i.e., \(Y_n=1\)) is \(s_{1,n}=\dfrac{n}{N}\) and for continuing observations

$$\begin{aligned} c_{1,n}=\sum _{k=n+1}^{N}\dfrac{n}{k(k-1)}\dfrac{k}{N} = \dfrac{n}{N}\sum _{k=n+1}^{N}\dfrac{1}{k-1}. \end{aligned}$$

Based on the above denotations and theory of optimal stopping, we have

$$\begin{aligned} u_{1,n}=\sup _{\tau \in {\mathcal {T}}_{2,n}}{\textbf{E}}_ns_{1,\tau }=\max \{s_{1,n},{\textbf{T}}u_{1,n}\}. \end{aligned}$$
(8)

2.2 Equilibrium States

Suppose that we are at some moment n, the value of the current candidate is x (seen for the Player II), it is relatively the best, and both players want to stop. If Player II gets the object (with probability \(1-p\)), his reward is \(s_{2,n}(x)\). With probability p, Player I gets the object, so Player II must continue the observations and receive the reward \(c_{2,n}(x)\). The situation in which in the future the opponent will find the best object is also included in the reward. A similar consideration gives us the reward for Player I. Let us denote the expected reward of Player II when he is choosing the state (n, x) which is local maximum (i.e., he effectively chooses the state (n, x)):

(9)

and the expected reward of Player I when he is choosing the state (n, x) which is local maximum, i.e., the relatively best at moment n:

(10)

Then the payoff matrix in the considered game is given by

$$\begin{aligned} (v_{1,n},v_{2,n}(x))= \begin{array}{c|c|c} \textrm{I} \backslash \textrm{II} &{} {S} &{} {F} \\ \hline {S} &{}(2p-1)w_{1,n};(1-2p)w_{2,n}(x) &{} w_{1,n};-w_{2,n}(x)\\ \hline {F} &{} -w_{1,n};w_{2,n}(x) &{} {{\textbf {T}}}v_{1,n},{{\textbf {T}}}v_{2,n}(x) \\ \end{array}, \end{aligned}$$
(11)

where \({\textbf{T}}\) stands for the one-step mean operator with respect to adequate Markov process transition probability (cf.  [25]).

In further analysis, comparisons of the value of payouts from the current state and the expected payouts resulting from the application of the selected strategy are performed. The technical lemma shows an example of the value of the second player’s payoff averaging operator in the event that he is interested in selecting the next potential candidate and his opponent does not interfere with it.

Remark 1

Let us assume for that \(X_n=\max \{X_1,X_2,\cdots ,X_n\}=x\). Then

$$\begin{aligned} {\hat{w}}_{2,n}(x)={{\textbf {T}}}{w}_{2,n}(x)&=\sum _{k=n+1}^{N} \int _x^1 w_{2,k}(y)p((n,x),(k,{\text {d}}y))\nonumber \\&=\sum _{s=1}^{N-n} s^{s-1}\int _x^1 w_{2,s+n}(y){\text {d}}y=\sum _{s=1}^{N-n} s^{s-1}{\tilde{w}}_{2,s+n}(x), \end{aligned}$$
(12)

where

$$\begin{aligned} {\tilde{w}}_{2,j}(x)&=\frac{1-x^{N-k+1}}{N-j+1}-\sum _{r=1}^{N-j}\frac{1}{(N-j+1)(N-j-r+1)}\nonumber \\&\quad +\sum _{r=1}^{N-j}\left[ \frac{x^{N-j-r+1}}{r(N-j-r+1)}-\frac{x^{N-j+1}}{r(N-j+1)}\right] . \end{aligned}$$
(13)

Since both players want to maximize their profits, we have the following conditions determining the states of observed process at which (S, S) is a Nash equilibrium:

$$\begin{aligned} {\left\{ \begin{array}{ll} (2p-1)w_{1,n}\geqslant -w_{1,n},\\ (1-2p)w_{2,n}(x)\geqslant w_{2,n}(x). \end{array}\right. } \end{aligned}$$

This leads to the inequalities

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _{j=n+1}^{N}\dfrac{x^{j-N-1}-1}{N-j+1}\leqslant 1,\\ \sum _{j=n+1}^{N}\dfrac{1}{j-1}\leqslant 1. \end{array}\right. } \end{aligned}$$

For player I, it is rational to stop when \(n\geqslant n^*\), and \(n^*\) is the standard optimal threshold (cf. [4]):

$$\begin{aligned} n^* = \max \left\{ 0\leqslant n \leqslant N: \sum _{k=n+1}^{N}\dfrac{1}{k-1} > 1 \right\} . \end{aligned}$$
(15)

Player II’s rational subset of states to stop are the same as in the standard one player optimal stopping problem also,

$$\begin{aligned} {{\textbf {D}}} = \{ (n,x) \in \{1,2,\cdots ,N\}\times [0,1]: X_n=x, x\geqslant x_n \}, \end{aligned}$$
(16)

where \(x_n\) is the solution of the equation \(w_{2,n}(x)=0\) in (0, 1] (cf. (9)),

  • for Player I, \( \tau _1 = \inf \lbrace n>n^*: Y_n=1 \rbrace \);

  • for Player II, \(\tau _2 = \inf \lbrace n>n^*:X_n=\max \lbrace X_1,\cdots ,X_n \rbrace =x \geqslant x_n \rbrace \).

Summarizing this analysis we have

Lemma 1

In the game described above, the strategy (S, S) is the pure Nash equilibrium if \(X_n\) is a local maximum and \(X_n\geqslant x_n\), \(n> n^*\).

Remark 2

The states after which players should accept the state (i.e., keep their participation in the game) in the completed construction can be modified. We are trying to find a pair of stopping moments in the Nash equilibrium. This description is included in Corollary 1.

Suppose that \(n>n^*\) and that the value of the current observation is \(X_n = x \leqslant x_n\) and its relative rank is 1. If we are below this threshold, then it is more optimal for Player II to change his strategy on F. The best response of Player I to the opponent’s strategy is to continue stopping if the expected future reward \({\textbf{T}}v_{1,n}\) is not greater than the actual reward \(w_{1,n}\). The player without information knows that the opponent has more information. Since the opponent chooses strategy \({{\textbf {F}}}\), we know that the present value of the object is less than the threshold \(x_n\). Suppose for a moment that we and Player I know this value and that it is x. If we knew this value, the future payoff would be

$$\begin{aligned} {\textbf{T}}(v_{1,n}\mid x)&= \sum _{k=n+1}^{N} x^{k-n-1} \left( \int _{x}^{x \vee x_k}{\mathbb {I}}_{(x,x \vee x_k]}(y) w_{1,k} {\text {d}}y + \int _{x\vee x_k}^{1} (2p-1)w_{1,k} {\text {d}}y\right) , \end{aligned}$$

where \(a\vee b = \max \{a,b \}\), \({\mathbb {I}}_{(s,t]}(y)=1\) when \(s<y\leqslant t\) and 0 otherwise, and \(w_{1,k}\) is given by (10). However, we have to average it. Knowing that the actual value is uniformly distributed on the interval \([0,x_n]\) (since the opponent wishes to continue the observations), we have

$$\begin{aligned} {\textbf{T}}v_{1,n} = \dfrac{1}{x_n}\int _{0}^{x_n} {\textbf{T}}(v_{1,n}\mid x) \textrm{d}x. \end{aligned}$$
(17)

Let us consider the set \( M_1=\{ n^*<n\leqslant N: Tv_{1,n} \leqslant w_{1,n} \}\). Note that this set in not empty. It contains the number \(\{ N\}\). Using the method of backward induction, we can find the lower bound for this set, i.e., the index \( {\tilde{n}}= \max \{n^*\leqslant n\leqslant N: Tv_{1,n} > w_{1,n}\}\). The consequence of this analysis is the conclusion:

Lemma 2

Suppose that the current state of the process \((n,X_n)\) is such that \(n\geqslant {\tilde{n}}, X_n=x \leqslant x_n\), and \(X_n\) is a local maximum. Then the strategy (S, F) is the pure Nash equilibrium in the game described above.

Now suppose that \(n={\tilde{n}}-1\) and the current state of the process is \(X_{{\tilde{n}}-1}=x\) where \(x\leqslant x_n\). Since Player I changes his strategy to F, it is necessary to check whether condition \({\textbf{T}}v_{2,n}(x) \geqslant w_{2,n}(x)\) is satisfied to have (F, F) the equilibrium. Indeed, it is true. Since now the reward \(w_{2,n}(x)<0\) and the future reward is positive for \(p<0.5\), it is more optimal to take an action F for the player II. Now the same consideration are made for \({\tilde{n}}-2, {\tilde{n}}-3,...\) etc. So, from this considerations, we have the conclusion.

Lemma 3

Suppose that the current state of the process \((n,X_n)\) is such that \(n\leqslant {\tilde{n}}, X_n=x \leqslant x_n\) and \(X_n\) is a local maximum. Then the strategy (F, F) is the pure Nash equilibrium in this state in the game described above.

Now consider the case when \(n=n^*-1\) and \(X_n=x > x_n\) is the local maximum. This is the opposite situation when the player II prefers to stop but the player I prefers to continue the observations without acceptance actual candidate. By analysis of the game matrix (11) at moment n, to find the subset of the state space where the strategy (F, S) is an equilibrium we compare the gain function for stopping at n and going forward (i.e., the gain function for the future). We have then

$$\begin{aligned} w_{2,n}(x)\geqslant {\textbf{T}}v_{2,n}(x). \end{aligned}$$
(18)

By (11) and the consideration of Remark 1, we have the left-hand-side of (18) as follows

$$\begin{aligned} {\textbf{T}}v_{2,n}(x)&=\sum _{k=n+1}^{N} x^{k-n-1} \bigg (\int _{x}^{x \vee x_k}{\mathbb {I}}_{(x,x \vee x_k]}(y) w_{2,k}(y) {\text {d}}y\nonumber \\&\quad + \int _{x\vee x_k}^{1} (1-2p)w_{2,k}(y) {\text {d}}y\bigg ). \end{aligned}$$
(19)

There is p such that the left-hand side of (18) is always bigger than the expression on the right-hand side, which is negative. Therefore, for \(n=n^*-1\) and, \(x>x_n\) it is better for player II to not change his strategy. Continuing these calculations, we get that it is also better to not change his strategy when \(n< n^*\) and \(x>x_n\).

Lemma 4

Suppose that the current state of the process \((n,X_n)\) is such that \(n< n^{*}, X_n=x >x_n\) and \(X_n\) is a local maximum. Then for big enough p the strategy (F, S) is the pure Nash equilibrium in the game described above.

Lemma 5

Suppose that the current state of the process \((n,X_n)\) is such that \(n< n^{*}, X_n=x \leqslant x_n\) and \(X_n\) is a local maximum. Then the strategy (F, F) is the pure Nash equilibrium in the game described above.

Based on the above lemmas, we conclude by the following corollary,

Corollary 1

In the best choice game with the asymmetric information, there exists a Stackelberg equilibrium point, and it is given in each subgame by Lemmas 1–5.

3 Numerical Example

3.1 Value of the Game

The value of the game for different values of priority parameter p and \(N=10\) is presented below.

$$\begin{aligned} \begin{aligned} ({\text {val}}_{1,10},{\text {val}}_{2,10})=&(0.002~01, 0.195~57), \quad p=0.1, \\ ({\text {val}}_{1,10},{\text {val}}_{2,10})=&(0.032~83, 0.128~96), \qquad p=0.25, \\ ({\text {val}}_{1,10},{\text {val}}_{2,10})=&(0.068~97, 0.087~96), \qquad p=\textrm{e}^{-1}, \\ ({\text {val}}_{1,10},{\text {val}}_{2,10})=&(0.136~62, 0.037~87), \qquad p=0.5. \end{aligned} \end{aligned}$$

3.2 Shift of the Threshold for Player I

Table 1 presents different values of the threshold \({\tilde{n}}\) for different horizons and values of the priority parameter p.

Table 1 Numbers \({\tilde{n}}\)
Full size table

4 Conclusion

The model presented in this work was created as a fruit of reflection on real problems in the field of business and finance. In the competition between two opponents from which one of them has access to more data we have found the equilibrium states. If the priority parameter of no-information player \(p\leqslant 0.5\), we have found that no-information player has to change his strategy in relation to the situation if he remained in the game alone. However, the full-information player does not intend to change his strategy. The numerical examples presented here are good presentation of the model.

It is worth adding that the importance of information in making strategic decisions when the task is dynamic and the decision maker is aware of this fact is a known research problem. In the optimal stopping problem, in the context of the role of information, it is worth mentioning the analyses in [28], or the problem of information valuation considered in the works [29, 30]. The game model considered in the work by Basu and Stettner [31] has a similar information structure. Players (agents) have partial knowledge about the state of the system, and this forces additional information filtering operations. This is additionally important because in the game under consideration, players take actions sequentially.

These examples show that further research on information modeling in multi-person decision-making processes in conjunction with modeling the psychological aspects of decision-making (v. [32]) is important both for the foundations of decision theory and for the development of probability theory methods.