Optimal Reinsurance and Investment Strategy with Delay in Heston’s SV Model

Abstract

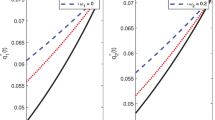
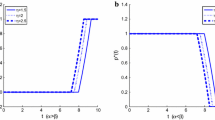
In this paper, we consider an optimal investment and proportional reinsurance problem with delay, in which the insurer’s surplus process is described by a jump-diffusion model. The insurer can buy proportional reinsurance to transfer part of the insurance claims risk. In addition to reinsurance, she also can invests her surplus in a financial market, which is consisted of a risk-free asset and a risky asset described by Heston’s stochastic volatility (SV) model. Considering the performance-related capital flow, the insurer’s wealth process is modeled by a stochastic differential delay equation. The insurer’s target is to find the optimal investment and proportional reinsurance strategy to maximize the expected exponential utility of combined terminal wealth. We explicitly derive the optimal strategy and the value function. Finally, we provide some numerical examples to illustrate our results.

Appendix

Lemma 1

Equation

$$\begin{aligned} c_{0}-\lambda \int _{0}^{\infty }c\mathrm{e}^{cu\gamma \mathrm{e}^{(\mu _{1}+\beta )(T-t)}}F(\mathrm{d}c)=0 \end{aligned}$$

(A1)

has a unique positive solution ${\hat{u}}$. If $c_{0}\leqslant \lambda \int _{0}^{\infty }c\mathrm{e}^{cu\gamma \mathrm{e}^{(\mu _{1}+\beta )(T-t)}}F(\mathrm{d}c)=0$, then the solution of Eq. (A1) satisfies $0<{\hat{u}}\leqslant 1$; if $c_{0}>\lambda \int _{0}^{\infty }ce^{cu\gamma \mathrm{e}^{(\mu _{1}+\beta )(T-t)}}F(dc)=0$, then the solution of Eq. (A1) satisfies ${\hat{u}}> 1$.

The proof of Lemma 1 is similar to Lemma 3.1 in Lin and Li [47], so we omit it.

The proof of Theorem 1

Assume that the HJB equation (16) has a classical solution J, which satisfies $J_{x}>0$ and $J_{xx}<0$. For maximizing the quantity in the HJB equation, by the first-order condition, we can derive the optimal investment strategy $\alpha ^{*}(t)$ as follows:

$$\begin{aligned} \alpha ^{*}(t)=-\frac{\eta J_{x}+\sigma \rho J_{xv}}{J_{xx}}. \end{aligned}$$

(A2)

Plugging (A2) into (16) yields

$$\begin{aligned}&\sup _{\pi \in \Pi }\{J_{t}+(\mu +c_{0}u+\mu _{1}x+\mu _{2}y+\mu _{3}z)J_{x} +\kappa (\zeta -v)J_{v}+(x-\delta y-\mathrm{e}^{-\delta h}z)J_{y}\nonumber \\&\qquad +\frac{1}{2}\sigma _{0}^{2}J_{xx} +\frac{1}{2}v\frac{(\eta J_{x}+\sigma \rho J_{xv})^{2}}{J_{xx}} +\frac{1}{2}\sigma ^{2}vJ_{vv}+\lambda \int _{0}^{\infty }[J(t,x-uc,y,v)\nonumber \\&\qquad -J(t,x,y,v)]F(\mathrm{d}c)\}=0, \end{aligned}$$

(A3)

with terminal condition

$$\begin{aligned} J(T,x,y,v)=U(x,y). \end{aligned}$$

Based on the form of the exponential utility function, we try the following form of value function J(t, x, y, v) as follows:

$$\begin{aligned} J(t,x,y,v)=-\frac{q}{\gamma }\exp \{-\gamma [a(t)(x+\beta y)-b(t)+g(t,v)]\} \end{aligned}$$

(A4)

with $a(T)=1$, $b(T)=0$, $g(T,v)=0$. Then

$$\begin{aligned} J_{t}= & {} -\gamma [a^{\prime }(t)(x+\beta y)-b^{\prime }(t)+g_{t}(t,v)]J, \qquad J_{x}=-\gamma a(t)J, \\ J_{y}= & {} -\gamma \beta a(t)J, \qquad J_{v}=-\gamma J g_{v}(t,v), \qquad J_{xx}=\gamma ^{2}a^{2}(t)J, \qquad J_{xv}=\gamma ^{2}a(t)J g_{v}(t,v), \\ J_{vv}= & {} (\gamma ^{2}g^{2}_{v}(t,v)-\gamma g_{vv}(t,v))J,\qquad J(t,x-cu,y,v)-J(t,x,y,v)=[\mathrm{e}^{cu\gamma a(t)}-1]J, \end{aligned}$$

here $a'(t),b'(t),g_{t}(t,v),g_{v}(t,v)$ denote the derivatives of a(t), b(t), g(t, v), and $g_{vv}(t,v)$ denotes the second-order derivatives of g(t, v) w.r.t. v. Introducing the above derivatives into (A3), we derive

$$\begin{aligned}&\sup _{\pi \in \Pi }\{a^{\prime }(t)(x+\beta y)-b^{\prime }(t)+g_{t}(t,v)+(\mu +c_{0}u+\mu _{1}x+\mu _{2}y+\mu _{3}z)a(t)\nonumber \\&\qquad +\kappa (\zeta -v)g_{v}(t,v) +(x-\delta y-\mathrm{e}^{-\delta h}z)\beta a(t)-\frac{1}{2}\sigma _{0}^{2}\gamma a^{2}(t)+\frac{ v}{2\gamma }(\eta -\sigma \rho \gamma g_{v}(t,v) )^{2} \nonumber \\&\qquad +\frac{1}{2}\sigma ^{2}v(\gamma g^{2}_{v}(t,v)-g_{vv}(t,v))+\frac{\lambda }{\gamma }\int _{0}^{\infty }[\mathrm{e}^{cu\gamma a(t)}-1]F(\mathrm{d}c)\}=0. \end{aligned}$$

(A5)

By the first-order condition, we have

$$\begin{aligned} c_{0}-\lambda \int _{0}^{\infty }c\mathrm{e}^{cu\gamma a(t)}F(\mathrm{d}c)=0. \end{aligned}$$

(A6)

According to Lemma 1, Eq. (A6) has a unique positive solution, we denote it by ${\hat{u}}$. Then plugging ${\hat{u}}$ into (A5) and simplifying, we have

$$\begin{aligned}&a^{\prime }(t)(x+\beta y)+a(t)((\mu _{1}+\beta )x+(\mu _{2}+\beta \delta )y) +a(t)(\mu _{3}-\beta \mathrm{e}^{\delta h})z \\&\qquad -b^{\prime }(t)+(\mu +c_{0}{\hat{u}})-\frac{1}{2}\sigma _{0}^{2}\gamma a^{2}(t) +\frac{\lambda }{\gamma }\int _{0}^{\infty }[\mathrm{e}^{c{\hat{u}}\gamma a(t)}-1]G(\mathrm{d}c) \\&\qquad +g_{t}(t,v)+\frac{1}{2}\frac{\eta ^{2}v}{\gamma }+[\kappa (\zeta -v)-\sigma \rho \eta v]g_{v}(t,v) -\frac{ 1}{2}\sigma ^{2}\gamma (1-\rho ^{2}) g_{v}^{2}(t,v)\\&\qquad +\frac{1}{2}\sigma ^{2}v g_{vv}(t,v)) =0. \end{aligned}$$

With the assumption of (18) and (19), we can get

$$\begin{aligned}&[a^{\prime }(t)+(\mu _{1}+\beta )a(t)](x+\beta y) \\&\qquad -b^{\prime }(t)+(\mu +c_{0}{\hat{u}})-\frac{1}{2}\sigma _{0}^{2}\gamma a^{2}(t) +\frac{\lambda }{\gamma }\int _{0}^{\infty }[\mathrm{e}^{c{\hat{u}}\gamma a(t)}-1]G(\mathrm{d}c) \\&\qquad +g_{t}(t,v)+\frac{1}{2}\frac{\eta ^{2}v}{\gamma }+[\kappa (\zeta -v)-\sigma \rho \eta v]g_{v}(t,v) -\frac{ 1}{2}\sigma ^{2}\gamma (1-\rho ^{2}) g_{v}^{2}(t,v)\\&\qquad +\frac{1}{2}\sigma ^{2}v g_{vv}(t,v)) =0. \end{aligned}$$

By the equation above, a(t), b(t) and g(t, v) meet the following differential equations:

Using the boundary condition $a(T)=0$, it follows from (5.7) that

$$\begin{aligned} a(t)=\mathrm{e}^{(\mu _{1}+\beta )(T-t)}. \end{aligned}$$

(A10)

Plugging (A10) into (5.8), we have

$$\begin{aligned} b^{\prime }(t)+(\mu +c_{0}{\hat{u}})+\frac{1}{2}\sigma _{0}^{2}\gamma \mathrm{e}^{2(\mu _{1}+\beta )(T-t)} -\frac{\lambda }{\gamma }\int _{0}^{\infty }[\mathrm{e}^{c{\hat{u}}\gamma \mathrm{e}^{(\mu _{1}+\beta )(T-t)}}-1]F(\mathrm{d}c)=0 \quad \quad \end{aligned}$$

(A11)

with $b(T)=0.$ If the distribution of C is known, then the expression form of b(t) can be derive explicitly.

To solve (5.9), we guess

$$\begin{aligned} g(t,v)=A(t)+B(t)v \end{aligned}$$

(A12)

with the boundary condition $A(T)=B(T)=0$. Thus,

$$\begin{aligned} g_{t}(t,v)=A^{\prime }(t)+B^{\prime }(t)v, \qquad g_{v}(t,v)=B(t),\qquad g_{vv}(t,v)=0. \end{aligned}$$

(A13)

Inserting (A13) into (5.9), we obtain

$$\begin{aligned} {}[A^{\prime }(t)+\kappa \zeta B(t)]+ {}[B^{\prime }(t)-\frac{\eta ^{2}}{2\gamma }+(\kappa +\sigma \rho \eta )B(t)-\frac{1}{2}\sigma ^{2}\gamma (1-\rho ^{2})B^{2}(t)]v=0. \end{aligned}$$

Matching coefficients yields

Firstly, we solve equation (5.14).

• (i) If $\rho =1$, (5.14) reduces to

  $$\begin{aligned} B^{\prime }(t)-(\kappa +\eta \sigma )B(t) +\frac{1}{2} \frac{\eta ^{2}}{\gamma }=0. \end{aligned}$$

  Considering $B(T)=0$, we can obtain

  $$\begin{aligned} B(t)=\frac{\eta ^{2}}{2\gamma (\kappa +\eta \sigma )} \bigg (1-\mathrm{e}^{-(\kappa +\eta \sigma )(T-t)}\bigg ). \end{aligned}$$

  (A16)

• (ii) If $\rho =-1$ and $\kappa \ne \eta \sigma$ (or $\kappa +\eta \sigma \rho \ne 0$), Eq. (5.14) reduces to (5.15) and has the same solution with (i); If $\rho =-1$ and $\kappa =\eta \sigma$ (or $\kappa +\eta \sigma \rho =0$), (5.14) reduces to

  $$\begin{aligned} B^{\prime }(t)+\frac{1}{2} \frac{\eta ^{2}}{\gamma }=0. \end{aligned}$$

  (A17)

  Using $B(T)=0$, we get the solution for (A17)

  $$\begin{aligned} B(t)=\frac{\eta ^{2}}{2\gamma }(T-t). \end{aligned}$$

  (A18)

• (iii) If $\rho \ne \pm 1$, let ${\bar{B}}(t)=-\frac{1}{2}\sigma ^{2}\gamma (1-\rho ^{2})B(t)$. Then, it follows from (5.14) that

  $$\begin{aligned} {\bar{B}}^{\prime }(t)+{\bar{B}}^{2}(t)-(\kappa +\eta \sigma \rho ) {\bar{B}}(t)-\frac{1}{2}\eta ^{2}\sigma ^{2}(1-\rho ^{2})=0. \end{aligned}$$

  (A19)

  Letting ${\bar{B}}(t)=\frac{\phi ^{\prime }(t)}{\phi (t)}$ (where $\phi (t)\ne 0$) and inserting it into (A19) yields

  $$\begin{aligned} \phi ^{\prime \prime }(t)-(\kappa +\eta \sigma \rho )\phi ^{\prime }(t) -\frac{1}{4}\eta ^{2}\sigma ^{2}(1-\rho ^{2})\phi (t)=0 \end{aligned}$$

  (A20)

  with $\phi (T)=1$ and $\phi ^{\prime }(T)=0$. We easily derive the solution of (A20)

  $$\begin{aligned} \phi (t)=\frac{\phi _{2}}{\phi _{2}-\phi _{1}}\mathrm{e}^{\phi _{1}t} +\frac{\phi _{1}}{\phi _{1}-\phi _{2}}\mathrm{e}^{\phi _{2}t}, \end{aligned}$$

  (A21)

  where

  $$\begin{aligned} \phi _{1,2}=\frac{\kappa +\eta \sigma \rho \pm \sqrt{(\kappa +\eta \sigma \rho )^{2} +\eta ^{2}\sigma ^{2}(1-\rho ^{2})}}{2}. \end{aligned}$$

  (A22)

  Furthermore,

  $$\begin{aligned} {\bar{B}}(t)=\frac{\phi ^{\prime }(t)}{\phi (t)} =\frac{\phi _{1}\phi _{2}-\phi _{1}\phi _{2}e^{-(\phi _{1}-\phi _{2})(T-t)}}{\phi _{2}-\phi _{1}\mathrm{e}^{-(\phi _{1}-\phi _{2})(T-t)}} \end{aligned}$$

  and

  $$\begin{aligned} B(t)=-\frac{2}{\sigma ^{2}\gamma (1-\rho ^{2})}{\bar{B}}(t) =-\frac{2}{\sigma ^{2}\gamma (1-\rho ^{2})} \frac{\phi _{1}\phi _{2}-\phi _{1}\phi _{2}\mathrm{e}^{-(\phi _{1}-\phi _{2})(T-t)}}{\phi _{2}-\phi _{1}\mathrm{e}^{-(\phi _{1}-\phi _{2})(T-t)}}. \end{aligned}$$

  In summary, the solution of (5.14) is

  $$\begin{aligned} {B(t)=}\left\{ \begin{array}{ll} -\frac{2}{\eta ^{2}\gamma (1-\rho ^{2})} \frac{\phi _{1}\phi _{2}-\phi _{1}\phi _{2}\mathrm{e}^{-(\phi _{1}-\phi _{2})(T-t)}}{\phi _{2}-\phi _{1}\mathrm{e}^{-(\phi _{1}-\phi _{2})(T-t)}}, \,\,\,\,\, \rho \ne \pm 1, \\ \frac{\delta ^{2}}{2\gamma (\kappa +\eta \sigma )} \bigg [1-\mathrm{e}^{-(\kappa +\eta \sigma )(T-t)}\bigg ], \,\,\,\, \qquad \rho =1, \\ \frac{\eta ^{2}}{2\gamma (\kappa -\eta \sigma )} \bigg [1-\mathrm{e}^{-(\kappa -\eta \sigma )(T-t)}\bigg ], \,\,\,\, \qquad \rho =-1 \,\, \text{ and } \,\, \kappa \ne \eta \sigma , \\ \frac{\eta ^{2}}{2\gamma }(T-t), \qquad \qquad \qquad \qquad \qquad \qquad \quad \rho =-1 \,\,\mathrm{and} \,\,\kappa =\eta \sigma . \\ \end{array}\right. \end{aligned}$$

  (A23)

  Further, we can get the solution of (5.14)

  $$\begin{aligned} \!\!\! {A(t)=}\left\{ \begin{array}{ll} \frac{2}{\sigma ^{2}\kappa \zeta \gamma (1-\rho ^{2})} \bigg (\phi _{1}(T-t)-\frac{\phi _{1}+\phi _{2}}{\phi _{1}-\phi _{2}} \ln \bigg |\frac{\phi _{2}-\phi _{1}}{\phi _{2}-\phi _{1}\mathrm{e}^{-(\kappa +\eta \sigma )(T-t)}}\bigg |\bigg ) , \,\,\,\, \rho \ne \pm 1, \\ -\frac{\eta ^{2}}{2\gamma \kappa \zeta (\kappa +\eta \sigma )} \bigg [(T-t)-\frac{1}{\kappa +\eta \sigma } \mathrm{e}^{-(\kappa +\eta \sigma )(T-t)} +\frac{1}{\kappa +\eta \sigma }\bigg ], \quad \rho =1, \\ -\frac{\delta ^{2}}{2\gamma \kappa \zeta (\kappa -\eta \sigma )} \bigg [(T-t)-\frac{1}{\kappa -\eta \sigma } \mathrm{e}^{-(\kappa -\eta \sigma )(T-t)} +\frac{1}{\kappa -\eta \sigma }\bigg ], \, \rho =-1 \,\, \mathrm{and} \,\, \kappa \ne \eta \sigma , \\ \frac{\delta ^{2}}{4\gamma \kappa \zeta }(T-t)^{2}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad \, \rho =-1 \,\,\,\mathrm{and} \,\,\kappa =\eta \sigma . \\ \end{array}\right. \end{aligned}$$

  (A24)

Therefore, we have derived the expressions of g(t, v) in (5.9) and value function J(t, x, y, v) in (A4). Combining (A2), (A4), (A10) and (A12), we obtain the optimal investment strategy

$$\begin{aligned} \alpha ^{*}(t)=\frac{\eta -\sigma \rho \gamma B(t)}{\gamma }\mathrm{e}^{-(\mu _{1}+\beta )(T-t)}, \end{aligned}$$

(A25)

where B(t) is given by (A23). Combining with Lemma 1, the theorem is proved.

The following is the proof of Theorem 2.

Proof

Let $Q=[0,\infty )\times [0,\infty )\times [0,\infty )$. Take a sequence of bounded open sets $Q_{1},Q_{2},Q_{3},\cdots$, with $Q_{i}\subset Q_{i+1}\subset Q, i=1,2, \cdots$, and $Q=\bigcup Q_{i}$. Denote the exit time of (X(t), Y(t), V(t)) from $Q_{i}$ by $\tau _{i}$. Thus, $\tau _{i}\wedge T \rightarrow T$ when $i\rightarrow \infty$.

For the wealth process $X^{\pi }(t)$, we can obtain

$$\begin{aligned}&\qquad \mathrm{d}\varPhi (t,X(t),Y(t),V(t))\\&={\mathscr {L}}^{\pi }\varPhi (t,X(t),Y(t),V(t))+\varPhi _{x}\sigma _{0}\mathrm{d}W_{0}(t)\\&\qquad \quad +\varPhi _{x}\alpha (t)\sqrt{V(t)}\mathrm{d}W_{1}(t)-\varPhi _{x}\mathrm{d}\bigg (\sum ^{N(t)}_{i=0}u(t)M_{i}\bigg ) +\varPhi _{v}\sigma \sqrt{V(t)}\mathrm{d}W_{2}(t). \end{aligned}$$

Using Itô’s formula on $\varPhi (t,X(t),Y(t),V(t))$ yields

$$\begin{aligned}&\quad \quad \varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))\\&= \varPhi (t,x,y,v)\qquad +\int _{t}^{\tau _{i}\wedge T}\varPhi _{v}\sigma \sqrt{V(s)}\mathrm{d}W_{2}(s) \\&\quad + \int _{t}^{\tau _{i}\wedge T}{\mathscr {L}}^{\pi }\varPhi (s,X(s),Y(s),V(s))\mathrm{d}s+\int _{t}^{\tau _{i}\wedge T}\varPhi _{x}\sigma _{0}\mathrm{d}W_{0}(s) \\&\quad + \int _{t}^{\tau _{i}\wedge T}\varPhi _{x}\alpha (t)\sqrt{V(t)}\mathrm{d}W_{1}(s)-\int _{t}^{\tau _{i}\wedge T}\varPhi _{x}\mathrm{d}\bigg (\sum ^{N(s)}_{i=0}u(s)M_{i}\bigg ). \end{aligned}$$

Because $\pi \in \Pi$, the terms $\int _{t}^{\tau _{i}\wedge T}\varPhi _{x} \sigma _{0}\mathrm{d}W_{0}(s),\, \int _{t}^{\tau _{i}\wedge T}\varPhi _{x}\alpha (t)\sqrt{V(t)}\mathrm{d}W_{1}(s), \int _{t}^{\tau _{i}\wedge T} \varPhi _{v}\sigma \sqrt{V(s)}\mathrm{d}W_{2}(s)$ on the right hand are square-integrable martingales with zero expectation. And with (4), we have

$$\begin{aligned}&E[\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))|X(t)=x,Y(t)=y,V(t)=v] \\ =&\,\varPhi (t,x,y,v)+E\bigg [\int _{t}^{\tau _{i}\wedge T}{\mathscr {L}}^{\pi }\varPhi (s,X(s),Y(s),V(s))\mathrm{d}s|X(t)\\ =&\,x,Y(t)=y,V(t)=v\bigg ]\\ \leqslant&\,\varPhi (t,x,y,v). \end{aligned}$$

In terms of Lemma in Larssen [35], the uniform integrability of $\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T)), i=1,2,\cdots$ yields

$$\begin{aligned} J(t,x,y,v)&=\sup _{\pi \in \Pi }E[U(X(T),Y(T))|X(t)=x,Y(t)=y,V(t)=v]\\&=\lim _{i\rightarrow \infty } E[\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))|X(t)\\&\quad =x,Y(t)=y,V(t)=v] \\&\leqslant \varPhi (t,x,y,v). \end{aligned}$$

Similarly, we have

$$\begin{aligned}&\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))\\= & {} \varPhi (0,x_{0},y_{0},v_{0}) +\int _{0}^{\tau _{i}\wedge T}\varPhi _{v}\sigma \sqrt{V(s)}\mathrm{d}W_{2}(s) \\&\quad +\int _{0}^{\tau _{i}\wedge T}{\mathscr {L}}^{\pi }\varPhi (s,X(s),Y(s),V(s))\mathrm{d}s +\int _{0}^{\tau _{i}\wedge T}\varPhi _{x}\sigma _{0}\mathrm{d}W_{0}(s)\\&\quad +\int _{0}^{\tau _{i}\wedge T}\varPhi _{x}\alpha (t)\sqrt{V(t)}\mathrm{d}W_{1}(s) -\int _{0}^{\tau _{i}\wedge T}\varPhi _{x}d\bigg (\sum ^{N(s)}_{i=0}u(s)M_{i}\bigg ). \end{aligned}$$

and then

$$\begin{aligned}&E[\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))] \\= & {} \varPhi (0,x_{0},y_{0},v_{0})+E\bigg [\int _{0}^{\tau _{i}\wedge T}{\mathscr {L}}^{\pi }\varPhi (s,X(s),Y(s),V(s))\mathrm{d}s\bigg ] \\\leqslant & {} \varPhi (0,x_{0},y_{0},v_{0}). \end{aligned}$$

Thus, for X(t), we have

$$\begin{aligned} \sup _{\pi \in \Pi }E[U(X(T),Y(T))]=&\lim _{i\rightarrow \infty } E[\varPhi (\tau _{i}\wedge T,X(\tau _{i}\wedge T),Y(\tau _{i}\wedge T),V(\tau _{i}\wedge T))] \\ \leqslant&\,\, \varPhi (0,x_{0},y_{0},v_{0}). \end{aligned}$$

For $\pi ^{*}=(u^{*}(t),\alpha ^{*}(t))$ and $X^{*}(t)$, all inequalities become equalities, i.e., $J(t,x,y,v)=\varPhi (t,x,y,v)$ and $\sup _{\pi \in \Pi }E[U(X^{*}(T),Y(T))]=\varPhi (0,x_{0},y_{0},v_{0})$. The proof is completed.