Abstract
In analyzing semi-continuous data, two-part model is a widely appreciated tool, in which two components are enclosed to characterize the mixing proportion of zeros and the actual level of positive values in semi-continuous data. The primary interest underlying such a model is primarily to exploit the dependence of the observed covariates on the semi-continuous variables; as such, the exploitation of unobserved heterogeneity is sometimes ignored. In this paper, we extend the conventional two-part regression model to much more general situations where multiple latent factors are considered to interpret the latent heterogeneity arising from the absence of covariates. A structural equation is constructed to describe the interrelationships between the latent factors. Moreover, a general statistical analysis procedure is developed to accommodate semi-continuous, ordered and unordered data simultaneously. A procedure for parameter estimation and model assessment is developed under a Bayesian framework. Empirical results including a simulation study and a real example are presented to illustrate the proposed methodology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In social surveys, semi-continuous data often occur when measurements have zeros and positive values. The dataset exhibits right skewness and excess kurtosis. Examples include household finance debt and assets (e.g., [5, 10]), in which zeros, unlike those in the censored data analysis, represent the actual level of debts held by the household. In understanding this type of data, the primary interest is to explore how many the zeros occur, how they are influenced by the exogenous factors, and what the actual values are, assuming that they are positive. In this scenario, two-part model (TPM, see, e.g., [8, 9, 29, 34]) provides a powerful tool. The basic formulation of TPM is the assumption that the whole model is composed of two parts: one is a binary process (Part one), usually formulated via logistic or probit regression model, to indicate the pattern of explanatory factors on the proportion of zeros, and the other is a continuous process (Part two), generally specified within a log-normal or log-skew-elliptical linear regression model [33], to describe the effects of covariates on the means of responses. These two parts are not separated from each other. Instead, they are combined in a mixed form. By integrating the binary model and continuous process into one, TPM provides a unified and flexible way to describe various relevances for semi-continuous data.
Over the past serval decades, much effort has been devoted to the extensions of conventional two-part model in different contexts, but most focuses on accommodating longitudinal and clustered data. For example, in the adolescent alcohol use research, Olsen and Schafer [34] extended a two-part model to a scenario where two correlated random effects were included to characterize the dependence of responses within a cluster. This routine was followed by Tooze, Grunwald and Jones [42] for analyzing medical expenditure panel data; recent advances include the selection of appropriate distributions for the continuous part to defend against distributional deviations and outliers; see, e.g., [25, 26, 33, 39] and among others. These methods have attracted significant attention to TPM for use in the behavioral science, economics, psychology and medicine in recent years.
The methods mentioned above are mainly confined to exploring the effects of the observed explanatory factors on the semi-continuous outcomes. The variability in responses is largely explained through the variability in the observed covariates. However, in real applications, it is impossible to accommodate all relevant observed factors into a model. In many circumstances, some unobserved or latent factors could have important impacts on the behavior of semi-continuous data. Broadly speaking, latent factors can be any random or fixed quantities in the model that cannot be measured directly. However, herein, we emphasize in a narrow sense that these factors have physical meanings and often represent various latent traits or concepts under consideration. Ignoring these latent factors will inflate unique errors and can easily results in poor fits.
Recently, some authors have developed semi-continuous data analysis within a latent variables framework. For example, in the study of children’s aggressive behavior, Kim and Muthén [22] noticed that an adolescent’s propensity to engage in aggressive behavior and exhibit highly aggressive activity levels has a significant influence on the children’s aggressive behavior. They constructed a two-part mixture factor analysis model to identify the relationships between latent factors and semi-continuous items. In distinguishing the influences of the frequency and intensity of health-related symptoms on the health care and treatment, Schneider and Stone [40] claimed that a two-part factor analysis model can be helpful for understanding health disparities and to track population trends in health and well-being over time. In the context of household finance, Feng et al. [10] proposed a two-part factor model with latent risk factors to investigate the effect of a family head’s financial literacy on the household’s investment strategy. They used binary indicators to manifest these risk factors and conducted simultaneous analysis with semi-continuous data. Within the multivariate longitudinal framework, Xia et al. [46] extended the above factor-analysis-based work to a general situation in which a dynamic structural equation was included to detect the possible transition pattern of factors over time. Recently, Wang et al. [44] developed a Bayesian variable selection procedure for the joint analysis of semi-continuous and ordinal categorical data within a structural equation modeling framework. Except for Xia et al. [46] and Wang et al. [44], the methods mentioned above more or less relied on factor analysis model, which may be challenging when the exploitation of interrelationships and/or casual effects between factors are required. Although Xia et al. [46] and Wang et al. [44] provided a general framework for semi-continuous data, their methods cannot be applied directly to situations where the mixed categorical outcomes are presented. In particular, the Bayesian variable selection procedure may not be very effective in assessing model fits.
In this paper, we propose a joint modeling for semi-continuous, ordered and unordered categorical data. Our proposal is seemingly similar to that of Wang et al. [44] but we focus on the joint analysis of the mixed categorical outcomes. Inclusion of mixed categorical data, especially multinomial data, apparently complicates the analysis from both computational and theoretical viewpoints. Our motivation stems from the study of the household debt and assets from the China Household Finance Survey(CHFS). Household debt and assets are the major items in household balance sheet around the world and play an important role in the national economies. They not only reflect the living standard of residents, but also serve as a barometer for the central bank to implement macroeconomic regulations, maintain financial stability and provide financial services. Over the last few years, widely well-studied literature has revealed that various latent factors, including household financial literacy [10, 37], family culture, and saving behavior (e.g., [3, 6]), have important impacts on the household finance assets and debts, including their amount and magnitude. However, to the best of our knowledge, no studies have provided a unified framework to assess their joint effects. Hence it is of practical interest to conduct simultaneous analysis, investigate joint effects on the household’s financial debts and assess interrelationships between multiple factors. We partition multiple latent factors into exogenous factors and endogenous factors, which, respectively, represents our knowledge about different aspects of financial traits. A structural equation is constructed to explore the interrelationship and/or causality between these factors. Because in the financial survey, these primary response variables cannot be measured directly, multiple questions or indicators related to these latent responses were required, which produced different types of outcomes. We developed a Bayesian analysis procedure for analyzing such data. An attractive feature of the Bayesian approach is its flexibility to utilize useful prior information to achieve better results. Moreover, simulation-based Bayesian methods depend less on asymptotic theory and hence have the potential to produce reliable results with small samples. We implemented Markov chains Monte Carlo (MCMC) sampling method to conduct posterior analysis. Gibbs sampler (e.g., [12, 16]) is used to draw observations from the target distribution. In view of the nonlinear functions related to latent quantities presented, we pursued the Pólya-Gamma (PG) augmentation technique [36] to facilitate posterior sampling. A key idea behind PG sampling is to recast the logistics regression model by its stochastic representation, which produces a closed form for full conditionals of latent factors and related parameters. It avoids the notorious tuning step in the Metropolis-Hastings algorithm (MH, [19, 31]) at a slight computational cost and improved the computation efficiency by virtue of its independent samples. Inferences about the parameter estimation and model comparison/assessment were based on these simulated observations.
The rest of the paper is organized as follows. Section 2 introduces the proposed model for semi-continuous data. Section 3 outlines the MCMC algorithm. Posterior inferences on the parameter estimation and model assessment are also presented in this section. A simulation study to assess the performance of the proposed model is given in Sect. 4. In Sect. 5, we apply the proposed method to the household finance debt study. Section 6 concludes the paper with a discussion.
2 Model Description
2.1 Two-Part Latent Variable Model with Mixed Data
Suppose that for subject/individual i \((i=1,\cdots ,N)\), \({\textbf{y}}_i=({\textbf{c}}_i^T, {\textbf{v}}_i^T)^T\) is a \(p\times 1\) mixed observed responses, where \({\textbf{c}}_i=(c_{i1},\cdots ,c_{ir})^T\) is an \(r\times 1\) observed semi-continuous vector and \({\textbf{v}}_i=(v_{i1},\cdots ,v_{is})^T\) is an \(s(=p-r)\times 1 \) observed categorical vector. For simplicity, we assume that each categorical variable \(v_{ik}\) takes a value in \(\mathcal {L}=\{0,1,\cdots , L\}\), of which each element indexes a category under consideration. Naturally, \(L=1\) corresponds to the binary case. Moreover, we follow the convention in the literature [34] and represent a semi-continuous variable by two surrogate variables: the occurrence variable \(u_{ij}\) and the intensity variable \(z_{ij}\), each defined as follows
where \(h(\cdot )\) is any monotonically increasing function that ensure that \(z_{ij}\) is approximatively normal. For example, \(h(\cdot )\) can be taken as the logarithm transformation which produces a log-normal distribution for \(z_{ij}\), but this is not necessary. In the cross-sectional or longitudinal setting, the semi-continuous variable is often formulated via specifying a logistic regression model for \(u_{ij}\) and a normal linear regression model for \(z_{ij}\), thus forming a two-part regression model for \(c_{ij}\). In this paper, our interest mainly concentrates on the joint analysis of \({\textbf{y}}_i\). To this end, we let \({\textbf{u}}_i=(u_{i1},\cdots ,u_{ir})^T\) and \({\textbf{z}}_i=(z_{i1},\cdots ,z_{ir})^T\), and assume that conditional upon an m-dimensional subject-specific latent factors \({\varvec{\omega }}_i\), the random vectors \({\textbf{u}}_i\), \({\textbf{z}}_i\) and \({\textbf{v}}_i\) are independent, each with the following sampling distribution:
where \({\varvec{\gamma }}_h=({\varvec{\gamma }}_{h_{1}}^T,\cdots ,{\varvec{\gamma }}_{h_{r}}^T)^T(h=1,2)\) denotes the \(r\times q_h\) regression coefficient matrix, \({\varvec{\beta }}_h=({\varvec{\beta }}_{h_{1}}^T,\cdots ,{\varvec{\beta }}_{h_{r}}^T)^T(h=1,2)\) is the \(r\times m\) factor loading matrix, and \({\varvec{\varLambda }}=({\varvec{\varLambda }}_1^T,\cdots ,{\varvec{\varLambda }}_s^T)^T\) is the \(s\times m\) factor loading matrix; \({\varvec{\mu }}=(\mu _1,\cdots ,\mu _s)^T\) is the intercept vector, \({\varvec{\varPsi }}_\epsilon =diag\{\psi _{\epsilon 1},\cdots ,\psi _{\epsilon r_i^*}\}\) and \({\varvec{\varPsi }}_\delta =diag\{\psi _{\delta 1},\cdots ,\psi _{\delta s}\}\) are the \(r_i^*\times r_i^*\) and \(s\times s\) diagonal scale matrices which perhaps are fixed and known; \(r_i^*\) is the size of the set \(\{j:u_{ij}=1\}\); \({\textbf{x}}_{hi}=(x_{hi1},\cdots ,x_{hiq_h})^T\) is individual-specific observed explanatory factors with \(x_{hi1}=1\). Without loss of generality, throughout this paper, we assume that \({\textbf{x}}_{1i}\) and \({\textbf{x}}_{2i}\) are identical.
Let \({\varvec{\omega }}_i=({\varvec{\eta }}_i^T,{\varvec{\xi }}_i^T)^T\) be a partition of \({\varvec{\omega }}_i\), where \({\varvec{\eta }}_i\) is the \(m_1\times 1 \) endogenous factors and \({\varvec{\xi }}_i\) is the \(m_2\times 1(m_1+m_2=m)\) exogenous factors. We identify the relationships among the latent factors through the following structural equation (e.g., [23])
where \(\textbf{B}(m_1\times m_1)\) and \({\varvec{\varGamma }}(m_1\times m_2)\) are the regression coefficient matrices representing the effects of \({\varvec{\eta }}_i\) and \({\varvec{\xi }}_i\) on \({\varvec{\eta }}_i\), respectively; \({\varvec{\zeta }}_i(m_1\times 1)\) is the vector of residuals, which has a normal distribution with mean zeros and diagonal covariance matrix \({\varvec{\varPsi }}_{\zeta }= diag\{\psi _{\zeta 1},\cdots ,\psi _{\zeta m_1}\}\); \({\varvec{\xi }}_i\sim N_{m_2}({\varvec{0}},{\varvec{\varPhi }})\) with \({\varvec{\varPhi }}(m_2\times m_2)>0\). We assume that \({\varvec{\zeta }}_i\) is independent of \({\varvec{\xi }}_i\). Furthermore, we follow the common routine in latent variable analysis (see, e.g., [23, 45, 46]) and assume that \(\textbf{B}_0={{\varvec{I}}}_{m_1}-\textbf{B}\) is nonsingular and its determinant is independent of the elements of \(\textbf{B}\). The latter assumption holds for all nonrecursive models in which \(\textbf{B}\) is an upper (or lower) triangular matrices. This assumption can be relaxed but at the expense of much computational effort. By letting \({\varvec{\varPi }}=(\textbf{B},{\varvec{\varGamma }})\), we can recast (2.5) as \({\varvec{\eta }}_i={\varvec{\varPi }}{\varvec{\omega }}_i+{\varvec{\zeta }}_i\). Although we prefer using the linear form for the structural equation, direct extension to the nonlinear model for factors or parameters is straightforward (see, e.g., [7, 24]).
We now turn to the joint distribution \(p({\textbf{v}}_i|{\varvec{\mu }},{\varvec{\varLambda }},{\varvec{\varPsi }}_\delta ,{\varvec{\omega }}_i)\). Generally, the categorical responses can be modeled in various ways, but each approach requires a specific model to simplify the implementation of the MCMC algorithm. In this paper, we resort to the latent response method. For ease of exposition, we assume that \({\textbf{v}}_i=({\textbf{v}}_{i1}^T,{\textbf{v}}_{i2}^T)^T\), where \({\textbf{v}}_{i1}\) is an \(s_1\times 1\) ordered categorial subvector and \({\textbf{v}}_{i2}\) is an \(s_2(=s-s_1)\times 1\) unordered categorical subvector. Correspondingly, we partition \({\varvec{\mu }}=({\varvec{\mu }}_1^T,{\varvec{\mu }}_2^T)^T\), \({\varvec{\varLambda }}=({\varvec{\varLambda }}_1^T,{\varvec{\varLambda }}_2^T)^T\) and \({\varvec{\varPsi }}_{\delta }=diag\{{\varvec{\varPsi }}_{\delta 1},{\varvec{\varPsi }}_{\delta 2}\}\), which correspond to the partition of \({\textbf{v}}_i\). We assume that given latent factors, \({\textbf{v}}_{i1}\) and \({\textbf{v}}_{i2}\) are independent, each with the sampling distribution \(p({\textbf{v}}_{id}|{\varvec{\mu }}_d,{\varvec{\varLambda }}_d,{\varvec{\varPsi }}_{\delta d},{\varvec{\omega }}_i)(d=1,2)\) given below.
For the ordinal variables \({\textbf{v}}_{i1}\), we introduce latent score variables \({\textbf{v}}_{i1}^*=(v_{i11}^*,\cdots ,v_{i1s_1}^*)^T\) such that
where \(v_{i1k}^*\)s, conditional on \({\varvec{\omega }}_i\), are distributed independently with the normal distribution \(N(\mu _{1k}+{\varvec{\varLambda }}_{1k}^T{\varvec{\omega }}_i,\psi _{\delta 1k})\), and \(-\infty =\alpha _{k,0}<\alpha _{k,1}<\cdots<\alpha _{k,L}<\alpha _{k,L+1}=+\infty \) are the thresholds used to index the categories. In this case, by conditioning on latent factors, the joint distribution of \({\textbf{v}}_{i1}\) is given by
where \(\varPhi (\cdot )\) is the standard normal distribution function and \({\varvec{\theta }}\) is the unknown parameter vector. Integrating out the latent factors produces the item dependence between any two ordinal variables in \({\textbf{v}}_{i1}\). An advantage underlying Expression (2.6) is that conditional on \({\textbf{v}}_{i1}\) and \({\varvec{\omega }}_i\), the conditional distribution of \({\textbf{v}}_{i1}^*\) is just the product of\(s_1\) univariate truncated normal distributions. This facilitates MCMC sampling in the posterior analysis.
For the multinominal variables \(v_{i2k}(k=1,\cdots ,s_2\)), the method given above may be inappropriate since the values \(\ell (=0,1,\cdots ,L)\) are just the proxies to index the category, not indicating any orders. To address this issue, for each \(v_{i2k}\), we introduce L utility variables (e.g., [41]) \({\textbf{v}}_{i2k}^*=(v_{i2k1}^*,\cdots ,v_{i2kL}^*)^T\) such that
where max(\({\textbf{v}}_{i2k}^*)\) denotes the largest element in vector \({\textbf{v}}_{i2k}^*\), \({\textbf{v}}_{i2k}^*\sim N_L({{\varvec{\nu }}}_k\vartheta _{i2k},\) \(\psi _{\delta 2 k}{{\varvec{R}}}_k)\), \({\varvec{\nu }}_k\) is the \(L\times 1\) vector, \(\vartheta _{i2k}=\mu _{2k}+{\varvec{\varLambda }}_{2k}^T{\varvec{\omega }}_i\), and \({{\varvec{R}}}_k\) is the \(L\times L\) covariance matrix. Let
be a partition of \(\mathbb {R}^L\), the L-dimensional Euclidean space. It can be shown that given \({\varvec{\omega }}_i\), the joint distribution of \({\textbf{v}}_{i2}\) has the form
where \(\varPhi _L(\cdot |{{\varvec{a}}},{\varvec{\varSigma }})\) refers to the L-dimensional normal probability distribution measure with mean vector \({{\varvec{a}}}\) and covariance matrix \({\varvec{\varSigma }}>0\). As discussed above, we prefer using (2.7) in that it provides a convenient and unified framework in the posterior sampling. In particular, this enables us to proceed with the analysis as one might for any multivariate normal data. Other choices for modeling nominal data can be found elsewhere (see, for example, [1, 36] and the references therein).
Expressions (2.2)- (2.7) provide a comprehensive modeling framework to understand the mixed data \(\textbf{y}_i\). The model constituted by Equations (2.2) and (2.3) describes the effects of observed and latent factors on the proportion of \(y_{ij}>0\) and actual values of positive \(y_{ij}\). The structural equation (2.5) and the measurement model (2.4) associated with (2.6) and (2.7) identify the interrelationships between multiple factors and the dependence of categorical outcomes on the latent factors. Such a modeling strategy not only provides a more feasible and flexible method in exploring extra heterogeneity among semi-continuous variables but also permits us to detect more subtle structure for mixed data.
For clarity of presentation, the following notation is introduced: \({{\varvec{U}}}=\{u_{ij}\}\), \({{\varvec{Z}}}=\{z_{ij}\}\), \({{\varvec{V}}}=\{v_{ik}\}\), \({{\varvec{X}}}=\{{\textbf{x}}_{hi}:h=1,2\}\), \({\varvec{\varOmega }}=\{{\varvec{\omega }}_i\}\), \({{\varvec{V}}}_1^*=\{v_{i1k}^*\}\) and \({{\varvec{V}}}_2^*=\{v_{i2k}^*\}\). Obviously, \({{\varvec{U}}}\) and \({{\varvec{Z}}}\) together specify the semi-continuous data. Furthermore, let \({\varvec{\theta }}\) denote the vector of all unknown parameters involved in the model. The joint distribution of \({{\varvec{U}}}\), \({{\varvec{Z}}}\), \({{\varvec{V}}}\), \({\varvec{\varOmega }}\), \({{\varvec{V}}}_1^*\) and \({{\varvec{V}}}_2^*\) is given by
where ‘\(tr{{\varvec{A}}}\)’ denotes the trace of a square matrix \({\varvec{A}}\), \({{\varvec{a}}}^{\otimes 2}={\varvec{a}}{\varvec{a}}^T\) for any column vector \({{\varvec{a}}}\) and \(I(\cdot )\) is the indicator function. Furthermore, based on the well-known identity in [36], we rewrite the logistic function (2.2) as follows
where \(\kappa _{ij}=u_{ij}-1/2\) and \(\vartheta _{ij}={\varvec{\gamma }}_{1j}^T{\textbf{x}}_{1i}+{\varvec{\beta }}_{1j}^T{\varvec{\omega }}_i\); \(p_{\textsc {PG}}(\cdot ) \) is the probability density function of PG distribution PG(1,0), specified by
where X is the PG(1,0) variable and \(E_k\)s are the iid. standard exponential random variables. In this case, we introduce \(N\times r\) independent PG(1,0) random variables \(u_{ij}^*\) and treat (2.9) as the marginal distribution of the following joint density:
Note that \(p_{\textsc {PG}}(u_{ij}^*)\) does not involve \({\varvec{\omega }}_i\) and \({\varvec{\theta }}\). Hence, the conditional distribution of \({\varvec{\omega }}_i\), given \(u_{ij}\), \(u_{ij}^*\) and \({\varvec{\theta }}\), is independent of \(p_{\textsc {PG}}(u_{ij}^*)\) and has a closed form. This facilitates the routines coding and also improves the computational efficiency (see Sect. 3). However, a disadvantage of Expression (2.10) is that the full conditional \(p(u_{ij}^*|u_{ij},{\varvec{\omega }}_i,{\varvec{\theta }})\) does not have a standard form. This incurs difficulty in the simulation of observations. The problem can be solved via indirect sampling methods such as rejection-acceptance sampling [18, 36] or slice sampling algorithm [43].
2.2 Identification Issue
It should be noted that the proposed model suffers from the models identification problem if no constraints are imposed on the model parameters. A parametric model is said to be identified if, for given data, the model is uniquely determined by unknown parameters. For our proposal, there are three resources resulting in model identification. The first is from the latent variable model in which the factor loading matrices are not identified. It is well known that the marginal model of observed data is invariant under some rotations of factor variables. Various methods have been proposed to eliminate such under-identifications. However, in most cases, indeterminacy problems are solved via imposing identification conditions on the parameter space (see, e.g., [4, 23]). One might set the parameters to fixed, known constants, most commonly zero. For example, one can restrict that \({\varvec{\varLambda }}^T{\varvec{\varPsi }}_{\delta }^{-1}{\varvec{\varLambda }}\) is diagonal or specify that \({\varvec{\varLambda }}\) is a lower-triangle matrix with its main-diagonal elements being positive. The elements in factor loadings also would be equal to one. The resulting estimates naturally depend on these constraints. In real applications, the constraints are usually introduced to facilitate model interpretation. In this paper, we follow Zhu and Lee’s method [47] and impose some restrictions on the factor loading matrices \({\varvec{\varLambda }}\), \({\varvec{\varGamma }}\) and/or covariance matrix \({\varvec{\varPhi }}\) by preassigning fixed values to them. This modeling strategy is very popular in the confirmatory factor analysis or within a linear structural equation relations (LISREL) framework. It allows us to explore the particular dependence of factors on the corresponding manifest responses.
The second resource of indeterminacy is related to modeling the ordered categorical data via (2.6), in which the thresholds \({\varvec{\alpha }}\), \({\varvec{\mu }}_1\) and \({\varvec{\varPsi }}_{\delta 1}\) are not simultaneously estimable. It can be easily shown that \(p({\textbf{v}}_{i1}|{\varvec{\omega }}_i,{\varvec{\theta }})\) is invariant under the affine transformation group. We address this indeterminacy by fixing \({\varvec{\varPsi }}_{\delta 1}\) to be an identity matrix and preassign fixed values to thresholds \(\alpha _{k1}\), and \(\alpha _{kL}\). To be specific, for every k, we set \(\alpha _{k1}=\varPhi ^{-1}(f_{k1})\) and \(\alpha _{kL} =\varPhi ^{-1}(f_{kL})\), where \(\varPhi (\cdot )\) is the standard Gaussian distribution function, and \(f_{k1}\) and \(f_{kL}\) are the frequencies of the first category, and the cumulative frequencies up to category \(v_{1ik} < L\), respectively. These restrictions have been appreciated in Bayesian analysis of structural equation models(SEMs) with ordered categorical variables, see, e.g.,[46].
The last indeterminacy comes from the modeling of unordered categorical data in (2.7). Apart from the similar reasons to those given above, the indeterminacy also underlies that the parameters in the distribution of \({\textbf{v}}_{2i}^*\) are identified up to \({\varvec{\nu }}_k\vartheta _{i2k}\) and \(\psi _{\delta 2k}{{\varvec{R}}}_k\). A simple method is to restrict \({\varvec{\nu }}_k={{\varvec{1}}}_L\) and \({{\varvec{R}}}_k={{\varvec{I}}}_L\), where \({{\varvec{1}}}_L\) is the \(L\times 1\) vector with all elements being unity and \({{\varvec{I}}}_L\) is the identity matrix of order \(L\times L\). This trick is also followed by [41] in the semi-parametric analysis of the latent variable model(LVM) with multivariate continuous and multinomial mixed data. Although other possible treatments can be available, we prefer using the above method for its simplicity.
Another issue involved in the current analysis is the determinacy of the number of latent factors. This problem is usually formulated within the framework of exploratory factor analysis (EFA) and confirmatory factor analysis (CFA). The basic formulation of EFA is that, for a given set of response variables, one seeks to search a smaller number of uncorrelated latent factors that will account for the correlations of the response variables so that when the latent factors are partialled out from the response variables, there no longer remain any correlations between them. In this scenario, the number of factors is not preassigned and is usually determined via model selection procedure, such as information criterion and hypothesis test procedures. Factor rotations are also required to obtain better interpretations. CFA is an extension of EFA and was developed by Jöreskog [20]. In this model, the factors are not necessarily correlated. The experimenter has already obtained from the substantive theory or exploratory analysis a certain amount of knowledge about the model and is in a position to formulate a more precise model. The factors and their number are usually determined in advance. The model is identified via fixing parameters, the resulting solution is directly interpretable, and the subsequent rotation of the factor loading matrix is not necessary.The goodness-of-fits of the posited models are compared to establish plausible model for substantive theory in the real world. Our development is more along the lines of the CFA, since the factors are determined by the experimenters via their knowledge about finance theory or the nature of problem under consideration.
3 Posterior Inference
3.1 Prior Elicitation
Due to the complexity of the model, we develop a Bayesian analysis procedure. The priors of the unknown parameters are required to complete Bayesian specifications. Let \({\varvec{\theta }}=\{{\varvec{\gamma }}_1,{\varvec{\beta }}_1,{\varvec{\gamma }}_2,{\varvec{\beta }}_2,{\varvec{\varPsi }}_\epsilon ,\) \({\varvec{\mu }},{\varvec{\varLambda }},{\varvec{\varPsi }}_\delta ,{\varvec{\varPi }},{\varvec{\varPsi }}_{\zeta }\), \({\varvec{\varPhi }}\), \({\varvec{\alpha }}\}\). Based on previous model configuration, it is natural to assume that the components of \({\varvec{\theta }}\) involved different models are independent, that is,
Moreover, let \(\widetilde{{\varvec{\gamma }}}_h=({\varvec{\gamma }}_h,{\varvec{\beta }}_h)\). According to suggestions in [47], the following commonly used conjugate types prior distributions are used in situations where we have rough ideas about the hyperparameters:
where ‘IG(a, b)’ is the inverse Gamma distribution with shape \(a>0\) and scale \(b>0\), and ‘\(IW(\rho ,{{\varvec{R}}}^{-1})\) is the inverse wishart distribution with hyper-parameters \(\rho \) and positive definite scale matrix \({{\varvec{R}}}^{-1}\); The scalars \(\alpha _{\epsilon 0j}\), \(\beta _{\epsilon 0j}\), \(\alpha _{\delta 0k}\), \(\beta _{\delta 0k}\), \(\alpha _{\zeta 0\ell }\),\(\beta _{\zeta 0\ell }\), \(\rho _0\), the vectors \(\widetilde{{\varvec{\gamma }}}_{h0j}(h=1,2)\), \({\varvec{\mu }}_0\) \({\varvec{\varLambda }}_{0k}\), \({\varvec{\varPi }}_{0\ell }\) and the matrices \({{\varvec{H}}}_{h0j}\), \({{\varvec{H}}}_{\delta 0k}\), \({{\varvec{H}}}_{\zeta 0\ell }\), \({\varvec{\varSigma }}_0\), and \({{\varvec{R}}}_0\) are assumed to be known. Thus, standard conjugate priors were specified for all components in the model. As pointed out by [46], the conjugate-type prior distributions are sufficiently flexible in most applications, and for situations with a reasonable amount of data available, the hyperparameters scarcely affect the analysis. In actual applications, the values of hyperparameters are often set to ensure that these priors tend to be noninformative to enhance the robustness of statistical inference.
3.2 MCMC Sampling
Let \({{\varvec{U}}}^*=\{u_{ij}^*\}\). In the discussion below, we suppress the covariates \({{\varvec{X}}}\) for notation simplicity. With the priors given in (3.1), the joint posterior distribution of \({\varvec{\theta }}\) is given by \(p({\varvec{\theta }}|{{\varvec{U}}},{{\varvec{Z}}}, {{\varvec{V}}})\propto p({{\varvec{U}}},{{\varvec{Z}}},{{\varvec{V}}}|{\varvec{\theta }})p({\varvec{\theta }})\), where
is the likelihood of the observed data. Because high-dimensional integrals are presented, no closed form can be available for this target distribution. We implement the MCMC sampling method. The latent quantities \(\{{{\varvec{U}}}^*, {{\varvec{V}}}, {{\varvec{V}}}_1^*,{{\varvec{V}}}_2^*,{\varvec{\varOmega }}\}\) are treated as the missing data and augmented with the observed data. The posterior analysis is carried out based on the joint distribution \(p({{\varvec{U}}}^*, {{\varvec{V}}}_1^*,{{\varvec{V}}}_2^*, {\varvec{\varOmega }},\) \({\varvec{\theta }}|{{\varvec{U}}},{{\varvec{Z}}})\). Gibbs sampler [12, 16] is used to draw observations from this target distribution. The sampling scheme essentially includes three types of moves: updating the components involved in the TPM, updating the components related to the measurement model, and updating the components pertaining to the structural equation model. We propose the following blocked Gibbs sampler, which iteratively simulates observations from the conditional distributions.
-
Step a: Generate \({\varvec{\varOmega }}\) from \(p({\varvec{\varOmega }}|{\varvec{\theta }},{{\varvec{U}}}^*,{{\varvec{V}}}_1^*,{{\varvec{V}}}_2^*,{{\varvec{U}}},{{\varvec{Z}}})\),
-
Step b: Generate \(\{{{\varvec{U}}}^*,\widetilde{{\varvec{\gamma }}}_1\}\) from \(p({{\varvec{U}}}^*,\widetilde{{\varvec{\gamma }}}_1|{\varvec{\varOmega }},{{\varvec{U}}})\),
-
Step c: Generate \(\{{\varvec{\alpha }},{{\varvec{V}}}_1^*\}\) from \(p({\varvec{\alpha }},{{\varvec{V}}}_1^*|{\varvec{\theta }},{\varvec{\varOmega }},{{\varvec{V}}})\),
-
Step d: Generate \({{\varvec{V}}}_2^*\) from \(p({{\varvec{V}}}_2^*|{\varvec{\theta }},{\varvec{\varOmega }},{{\varvec{V}}})\),
-
Step e: Generate \(\{\widetilde{{\varvec{\gamma }}}_2,{\varvec{\varPsi }}_{\epsilon }\}\) from \(p(\widetilde{{\varvec{\gamma }}}_2,{\varvec{\varPsi }}_\epsilon |{\varvec{\varOmega }},{{\varvec{U}}}, {{\varvec{Z}}})\),
-
Step f: Generate \({\varvec{\mu }}\) from \(p({\varvec{\mu }}|{\varvec{\theta }},{\varvec{\varOmega }},{{\varvec{V}}}_1^*,{{\varvec{V}}}_2^*)\),
-
Step g: Generate \(({\varvec{\varLambda }},{\varvec{\varPsi }}_{\delta })\) from \(p({\varvec{\varLambda }},{\varvec{\varPsi }}_{\delta }|{\varvec{\varOmega }},{{\varvec{V}}}_1^*,{{\varvec{V}}}_2^*)\),
-
Step h: Generate \(({\varvec{\varPi }},{\varvec{\varPsi }}_{\zeta })\) from \(p({\varvec{\varPi }},{\varvec{\varPsi }}_{\zeta }|{\varvec{\varOmega }})\),
-
Step i: Generate \({\varvec{\varPhi }}\) from \(p({\varvec{\varPhi }}|{\varvec{\varOmega }})\),
in which the redundant variables are removed from the conditioning set either by explicit integration or by conditional independence. For example, when drawing \(\{{\varvec{\alpha }},{\textbf{V}}_1^*\}\) in Step c, it follows from the model structure that the conditional distribution of \(\{{\varvec{\alpha }},{\textbf{V}}_1^*\}\), given the remain quantities, only depends on \({\varvec{\mu }}\), \({\varvec{\varLambda }}\), \({\varvec{\varPsi }}_\delta \), \({\varvec{\varOmega }}\) and \({{\varvec{V}}}\). Further, by multiple principal, we produce the draw of \(\{{\varvec{\alpha }},{\varvec{V}}_1^*\}\) by first sampling \({\varvec{\alpha }}\) from \(p({\varvec{\alpha }}|{\varvec{\mu }},{\varvec{\varLambda }},{\varvec{\varPsi }}_\delta ,{\varvec{\varOmega }},{{\varvec{V}}})\) and then sampling \({{\varvec{V}}}_1^*\) from \(p({{\varvec{V}}}_1^*|{\varvec{\alpha }},{\varvec{\mu }},{\varvec{\varLambda }},{\varvec{\varPsi }}_\delta ,{\varvec{\varOmega }},{{\varvec{V}}})\). The variables \({{\varvec{V}}}_1^*\) in the conditional distribution of \({\varvec{\alpha }}\) are integrated out to accelerate the mixing of MCMC samples. Note that except for the threshold parameters \({\varvec{\alpha }}\) and the latent variables \({{\varvec{U}}}^*\), the full conditionals involved in Steps (a)-(i) are all standard. Hence, simulating observations from them is straightforward and fast. However, under (3.1), the full conditional of \({\varvec{\alpha }}\) are not standard. We implement MH algorithm [19, 31] to update \({\varvec{\alpha }}\). The full conditionals and the technical sampling detail are given in “Appendix I.”
It follows from the standard Markov chains Monte Carlo theory (see, e.g., [16, 17]) that the sequence of simulated observations \(\{({{\varvec{U}}}^{*(\kappa )}, {{\varvec{V}}}_1^{*(\kappa )},\) \({{\varvec{V}}}_2^{*(\kappa ) },\) \({\varvec{\varOmega }}^{(\kappa )},{\varvec{\theta }}^{(\kappa )})\}\) converges at an exponential rate to the desired posterior distribution. The convergence of the blocked Gibbs sampler can be monitored by observing the values of estimated potential scale reduction (EPSR, [15]) and/or plotting the traces of the estimates for different starting values.
Simulated observations obtained from the posterior can be used for statistical inference via straightforward analysis procedure. For example, the joint Bayes estimates of \({\varvec{\theta }}\) and \({\varvec{\varOmega }}\) can be obtained via sample means of the generated observations as follows:
The consistent estimates of covariance matrix of estimates can be obtained via corresponding sample covariance matrices.
In general, inference from correlated observations is less precise than that from the same number of independent observations. To obtain a less correlated sample, observations may be collected in cycles with indices \(K_0+c, K_0 +2c,\cdots , K_0+Kc\) for some spacing c (see [12]), where \(K_0\) is the burn-in iteration. However, in most practical applications, a small c will be sufficient for many statistical analyses, such as getting estimates of the parameters and standard errors. In the numerical illustrations, we use \(c = 1\). Further discussions on thinning Markov chains outputs can be found, for example, in [17, 35] and the references therein.
The total number of draws, K, required for statistical analysis depends on the form of the posterior distribution and generally should be taken to be long enough to obtain adequate precision in the estimators. The most straightforward informal method for determining run length is to run several chains in parallel, with different starting values, and compare the estimates across chains. If they do not agree adequately, the length of K must be increased. Based on our empirical experiences, 2000 draws after convergence are sufficient. Clearly, different choice of K would not produce equal estimates wholly.
3.3 Model Selection and Assessment
Beyond the estimate issue, a critical point underlying the Bayesian analysis is to assess the accuracy of various model fits and explore the directions for improvement. It should be recognized that any posterior inference is made conditionally on the collection of assumptions implicit in the modeling. These assumptions are typically made for convenience and should be investigated with caution in the subsequent modeling processes. It is possible that the patterns of the observed data may be inconsistent with the model, and one must devise alternative assumptions that provides a better fit. In the model defined by equations (2.2) and (2.3) associated with measurement model (2.4), it is, for instance, of practical interest to select particular parametric structures of \({\varvec{\beta }}_d\) in (2.2)–(2.3) and/or \({\varvec{\varLambda }}\) in (2.4) to determine whether the effects of latent factors on the manifest variables exist. It is also important to examine whether or not latent variable models with structure equation are appropriate for improving the model fit.
In situations with plausible alternative models present, the Bayesian paradigm provides a useful methodology for assessing the sensitivity to model assumptions as well as criticizing different assumptions. Consider the situation in which there exist two plausible models \(M_0\) and \(M_1\), which may be nested or non-nested for the observed data \({{\varvec{D}}}=\{{{\varvec{U}}},{{\varvec{Z}}},{{\varvec{V}}}\}\). Let \(p({{\varvec{D}}}|{\varvec{\theta }},M_k)\) be the sampling density of \({{\varvec{D}}}\) and \(p({\varvec{\theta }}|M_k)\) be the prior density of \({\varvec{\theta }}\) under \(M_k\), coupled with the complete-data likelihood \(p({{\varvec{D}}},{{\varvec{Q}}}|{\varvec{\theta }},M_k)\). Here we use the notation \({{\varvec{Q}}}\) to signify the latent quantities contained in \(M_k\) (the subscript k for \({\varvec{\theta }}\) and \({{\varvec{Q}}}\) in \(M_k\) is omitted for notation simplicity). A sophisticated way to perform a model assessment between \(M_0\) and \(M_1\) is by using the Bayes factor (BF, e.g., [2, 21]), which is defined as the ratio of the marginal likelihoods of observed-data under each competing model, i.e.,
where \(p({{\varvec{D}}}|M_k)\) is the marginal likelihood of \({\varvec{D}}\) under \(M_k\). In general, BF is a summary of evidence provided by the data in favor of \(M_1\) as oppose to \(M_0\) or in favor of \(M_0\) to \(M_1\). Hence, a null hypothesis associated with \(M_0\) may be rejected, as may the alternative hypothesis associated with \(M_1\). At this point, the BF-based judgment is different from the classic p-value-based significance test approach which provides evidence on rejecting the null model.
Apparently, the calculation of \(\text {BF}_{10}\) or \(\log \text {BF}_{10}\) requires the evaluation of high-dimensional integrations of the likelihood with respect to \({{\varvec{Q}}}=\{{\varvec{\varOmega }},{{\varvec{V}}}_1^*,\) \({{\varvec{V}}}_2^*\}\) and \({\varvec{\theta }}\). The difficulty can be addressed via Monte Carlo approximations (see Chapter Five in [23] for a review). Among various well-developed methods, we resort to path sampling [13]. A useful feature underlying path sampling is that the logarithm scale of Bayes factor is computed, which is generally more stable than the ratio scale. Also, it is more effective when two competing models are far separated in the sense that the parameter spaces overlap less.
An alternative to model selection is to compare the logarithms of the pseudo-marginal likelihoods (LPML) [11, 32], defined as
where \(\text {CPO}_i = p({{\varvec{d}}}_i|{{\varvec{D}}}_{(i)})\) is known as the conditional predictive ordinate (CPO) given by
The last equality in above expression holds because given \({\varvec{\theta }}\), the variables \({{\varvec{d}}}_i\) are mutually independent. Here, \({{\varvec{D}}}_{(i)}\) is the dataset \({{\varvec{D}}}\) with \({{\varvec{d}}}_i\) removed and \({\varvec{d}}_i\) is the vector of observations from individual i. From (3.4), we can see that CPO\(_i\) is the marginal posterior predictive density of \({{\varvec{d}}}_i\) given \({{\varvec{D}}}_{(i)}\) and can be interpreted as the height of this marginal density at \({{\varvec{d}}}_i\). Thus, small values of LPML imply that \({{\varvec{D}}}\) does not support the model.
Based on the MCMC samples \(\{{\varvec{\theta }}^{(\kappa )}:\kappa =1,\cdots ,K\}\) already available in the estimation, a consistent estimate for LPML can be obtained via ergodic average given by
It is noted that under our proposal,
has no explicit form. We resort to the Monte Carlo approximation again. Specifically, given the current values \({\varvec{\theta }}^{(\kappa )}\) at the \(\kappa \)-th iteration, we draw H independent observations \(\{{\varvec{\omega }}_{ih}^{(\kappa )}:h=1,\cdots ,H\}\) from \(t_\nu ({\varvec{0}},{\varvec{\varSigma }}_\omega ({\varvec{\theta }}^{(\kappa )}))\), where \(t_\nu ({\varvec{0}},{{\varvec{A}}})\) denotes the multivariate t-distribution with degrees of freedom \(\nu \), location zero and the scale matrix \({{\varvec{A}}}> 0\). Then we can evaluate (3.6) at the observation \({{\varvec{d}}}_i\) through a weighted average:
where the factors \(w_{ih}^{(\kappa )}\) are the importance weights given by
with \(C_m(\nu )=\frac{\varGamma (\nu /2)(\nu /2)^{m/2}}{\nu ^{(\nu +m)/2}\varGamma ((\nu +m)/2)}\) and \({\varvec{\varSigma }}_\omega ^{(\kappa )}={\varvec{\varSigma }}_\omega ({\varvec{\theta }}^{(\kappa )})\) given by
In the implementation of the above sampling, the sample size H can be taken as varying with \(\kappa \). For example, we can take small value for H at the initial iterations and then increase its value when \(\kappa \) is large. By our experience, \(H=100\) is enough for achieving the sufficient accuracy of the approximation.
4 Simulation Study
In this section, the results of a simulation study are presented to demonstrate the empirical performance of the proposed Bayesian approach. The main objection is to assess the accuracy of the proposed procedure in terms of the estimation of unknown parameters and to investigate the model fits when various assumptions of the model are violated. The simulation design is given as follows. We consider the situation where one semi-continuous variable and six categorical manifest variables were included in the TPM given by (2.2)-(2.3) and the measurement model (2.4), respectively. Each was associated with three latent factors: one endogenous factor \(\eta _i\) and two exogenous factors \(\xi _{i1}\), \(\xi _{i2}\), i.e., \({\varvec{\omega }}_i=(\eta _i,\xi _{i1},\xi _{i2})^T\). The first four manifest variables were binary, and the last two were ordinal with four categories. The fixed covariates were taken as \({\textbf{x}}_{1i}=(1, x_{1i1}, x_{1i2})^T\) and \({\textbf{x}}_{2i}=(1, x_{2i1}, x_{2i2})^T\), in which the \(x_{1i\kappa }\)s were drawn independently from the standard normal distribution, whereas \(x_{2i\kappa }s\) were generated independently from the Bernoulli distribution with the success probability 0.3. The structural equation (2.5) was taken with the following form:
with \((\xi _{i1},\xi _{i2})\sim N_2({\varvec{0}},{\varvec{\varPhi }})({\varvec{\varPhi }}>0)\). The true values of the population parameters involved in the two-part models were selected as follows: \({\varvec{\gamma }}_1=(0.7,0.7,0.7)^T\), \({\varvec{\gamma }}_2=(0.8,0.8,0.8)^T\), \({\varvec{\beta }}_1={\varvec{\beta }}_2=(1.0^*,0.8,0.8)^T\) and \(\psi _\epsilon =1.0\), where the elements with an asterisk were treated as fixed for model identification. The population values of the unknown parameters involved in the measurement model and structural equation were set as: \({\varvec{\mu }}=0.8\times {{\varvec{1}}}_6\), \((\varGamma _1,\varGamma _2)=(0.8,0.8)\), \(\psi _\zeta =1.0\),
where the elements 0 and 1 in \({\varvec{\varLambda }}\) and \({\varvec{\varPhi }}\) are treated as fixed for identifying model and also for determining the scales of the latent factors, rather than estimating them. The threshold parameters were taken as \(\alpha _j=(-1.5^*,-0.8,0.6,1.0^*)(j=5,6)\). Thus, the total number of population parameters involved are 28. Based on these settings, we generated latent factors \({\varvec{\omega }}_i\) by first generating \(\xi _{i1},\xi _{i2}\) from \(N_2({\varvec{0}},{\varvec{\varPhi }})\) and then drawing \(\eta _i\) based on the structural equation (4.1). Conditional upon these generated latent factors, we draw occurrence variables variables \(u_{ij}\), intensity variables \(z_{ij}\) and manifest variables \(v_{ij}\) from the two-part model and the measurement model, respectively, thus forming the observed data \({{\varvec{U}}}\), \({{\varvec{Z}}}\) and \({{\varvec{V}}}\). To investigate the effects of sample size on the accuracy of estimates of unknown parameters, we selected \(N=2000\) and 5000, which, respectively, denote the moderate and large levels for the sample sizes. Note that there are in total \(2^4\times 4^2=256\) cells in the categorial variables. Too small sample size may not be appreciated in the current analysis.
For the Bayesian analysis, the following two kinds of inputs for the hyperparameters involved in the prior distributions (3.1) were considered, each representing our belief on the parameters a prior: (BAY I) \(\widetilde{{\varvec{\gamma }}}_{10}=\widetilde{{\varvec{\gamma }}}_{20}={{\varvec{0}}}_6\), \({{\varvec{H}}}_{10}={{\varvec{H}}}_{20}=100\times {{\varvec{I}}}_6\), \(\alpha _{\epsilon 0}=\beta _{\epsilon 0}=0.001\); \({\varvec{\mu }}_0={{\varvec{0}}}_6\), \({\varvec{\varSigma }}_0=100\times {{\varvec{I}}}_6\); the entries in \({\varvec{\varLambda }}_{0j}\), \({\varvec{\varGamma }}_{0k}\), which corresponded to the free parameters in \({\varvec{\varLambda }}\) and \({\varvec{\varGamma }}\), were set to be zeros; \({{\varvec{H}}}_{\delta 0k}\) and \({{\varvec{H}}}_{\zeta 0\ell }\) were diagonal matrices with the diagonal elements equal to 100. In addition, \(\alpha _{\delta 0k}=\alpha _{\zeta 0\ell }=0.001\), \(\beta _{\delta 0k}=\beta _{\zeta 0\ell }=0.001\), \(\rho _0=1.0\) and \({{\varvec{R}}}_0=100\times {{\varvec{I}}}_2\). Note that these values ensured that the priors were more inflated and approximately noninformative; this setting also represents a situation with inaccurate prior information. (BAY II) the components in \(\widetilde{{\varvec{\gamma }}}_{h0}(h=1,2)\), \({\varvec{\varLambda }}\) and \({\varvec{\varGamma }}\) were set to be the true population values in \({\varvec{\varLambda }}\) and \({\varvec{\varGamma }}\); \({\varvec{\varSigma }}_0\), \({{\varvec{H}}}_{h0}(h=1,2)\), \({{\varvec{H}}}_{\delta 0k}\) and \({{\varvec{H}}}_{\zeta 0\ell }\) were all taken as identity matrices; in addition, \(\alpha _{\epsilon 0}=\alpha _{\delta 0 k}=\alpha _{\zeta \ell }=9.0\), \(\beta _{\epsilon 0}=\beta _{\delta 0 k}=\beta _{\zeta \ell }=8.0\), \(\rho _0=10\), and \({{\varvec{R}}}_0^{-1}=7.0\times {{\varvec{I}}}_2\). The others were the same as those used in BAY (I). This can be regarded as a situation with good prior information and would be expected to provide better estimates for the unknown parameters. Discussions on the choices of hyperparameters are presented in “Appendix II.”
The proposed algorithm given in Sect. 3 is implemented to produce the Bayesian solutions for 100 replications. We used the MH algorithm to draw threshold parameters and the PG argumentation technique to sample latent factors and regression coefficients involved in the logistic model. We set \(\sigma _{\alpha _{jk}}=0.01\) for \(j=5,6\) in the proposal distributions which yielded approximate acceptance rates 0.32. Before the formal implementations, a few test runs were conducted as pilots to monitor the convergence of the Gibbs sampler. We plotted the values of EPSR [13] of the unknown parameters against the number of iterations for three different starting values under various settings. Figure 1 shows the plots of values of the EPSR of unknown parameters versus the number of iterations under BAY (I) with sample size 5000.
The estimates converged in less than 1500 iterations and the values of EPSR were less than 1.2. To be conservative, we collected 3000 observations after removing the initial 2000 observations as burn-in for computing the bias (BIAS), the root mean squares (RMS) and the standard deviation (SD) of the estimates for 00 replications. The BIAS and RMS of the jth component \(\widehat{\theta }_j\) in the estimates were calculated as follows:
where \(\theta _j^0\) is the jth element of the true population parameters \({\varvec{\theta }}^0\) and \(\bar{\theta }_j=\sum _{\kappa =1}^{100}/100\) represents the sample means. The results of estimates of common parameters across four fittings are shown in Tables 1 and 2, where the sums of the SD and RMS across the estimates are presented in the last rows.
Based on the results reported in Tables 1 and 2, we made the following observations: (i) the estimates BAY II were better than BAY I, but the differences were not significant. Both BAY I and BAY II yielded reasonable results. Hence, the effects of the hyperparameter values are minor. (ii) As expected, increasing the sample size improved the accuracy of the estimates and reduced the differences between the different types of Bayesian estimates. (iii) Comparatively, estimates corresponding to the parameters relating to the two-part model were less than accurate when N was relatively small. This was not surprising since Part one involved the binary data and Part two conditions upon Part one, which provided less information when exploring the true values. However, the accuracy was significantly improved when the sample size reached 5000.
Another simulation was conducted to examine the performance of the BF and LPML in selecting the competing models under consideration when the posited models were deviated away from the true model. In this study, the set-ups of the simulation design were set to be the same as those in the estimation procedure, but the manifest variables consisted of three binary variables, two ordered categorical variables and two ordered categorical variables, which were analogous to those in the real example. Correspondingly, the factor loading matrix was modified to
where as before, the elements 0 and 1 were treated as fixed for model identification. The sample size was taken as \(N=2000\).
Because latent variables play a crucial role in identifying the influence on the TPM, for model comparison, we considered the following competing models:
where ‘full model’ \(M_1\) denotes the true model corresponding to the generating mechanism of data; \(M_2\) and \(M_3\) represent the effects of latent factors imposed on the two parts of the TPM, \(M_4\) denotes two separated models: the ordinary two-part regression model for semi-continuous data and the conventional latent model for categorical manifest variables, and \(M_5\) focuses upon the particular structure on the structural equation. Note that except for \(M_5\), these models are not nested within each other since some elements were fixed in the unknown parameters.
The BF and LPML measure introduced beforehand were used to compare these competing models. In the calculation of the BF, defining a suitable \(M_{\lambda }\) is usually straightforward in the path-sampling algorithm but has to approach on a problem-by-problem basis. In practice, a convenient reference model, say \(M_0\), is often defined. The BF between two competing models \(M_j\) and \(M_k\) can be obtained via the identity \(\log \text {BF}_{jk}=\log \text {BF}_{j0}-\log \text {BF}_{k0}\). For our problem, we referred to the full model \(M_1\) as the reference and compare it with the other models. Thus, we related \(M_1\) to other competing models by constructing corresponding linked models as follows: for \(\lambda \in [0,1]\),
Clearly, \(M_{\lambda }^{(1,\kappa )}\) corresponded to \(M_1\) when \(\lambda =1\) and was reduced to \(M_{\kappa }(\kappa =2\cdots ,5)\) when \(\lambda =0\). The path sampling procedure was implemented using 20 equal-span grid elements in [0, 1]. The values of the hyperparameter \(\widetilde{{\varvec{\gamma }}}_{hj0}(h=1,2)\), \({\varvec{\mu }}_0\), \({\varvec{\varLambda }}_{0j}\), and \({\varvec{\varPi }}_{0j}\) were all fixed to be zero, \({{\varvec{H}}}_{h0j}\), \({\varvec{\varSigma }}_0\), \({{\varvec{H}}}_{\delta 0k}\), \({{\varvec{H}}}_{\zeta 0\ell }\) and \({{\varvec{R}}}_0\) were all taken as the identity matrices, and \(\rho _0=10\). These inputs were also used to calculate LPML. Though BF was sensitive to the choices of the prior, our experience showed that the inputs of the hyperparameters scarcely affected the resulting selection. We also observed that the time series of simulated observations in the calculation of \(U_{\lambda }\) converged in less than 200 iterations. Hence, at each \(\lambda _s\), a total of \(M=200\) observations were collected after discarding 1000 iterations. For the LPML, we selected 100 observations of \({\varvec{\omega }}_i\) after the convergence of Gibbs sampler to calculate the CPO. The resulting summary of the logarithms of the BFs and the LPMLs across 100 replications is given in Tables 3 and 4 where ‘SD’ denotes the standard deviation.
Examination of Tables 3 and 4 shows that \(M_1\) outperformed others uniformly (see row three in Table 3). Hence, the full model was selected. This also agreed with the true situation. We also found that \(M_4\) provided poor fit when compared to other competing models. The underlying reason perhaps was that under our framework, Equations (2.2)–(2.4) played dominant roles in the whole model. Another interesting fact lies in that \(M_5\) was more appreciated when compared to \(M_j:(j=2,,\cdots ,4)\). This conclusion was drawn because the partial-information underlying the data may not provides decisive evidence against \(M_5\).
In summary, our simulation results indicated that our MCMC algorithm did well in recovering the true parameters. In addition, our model adequacy test function and the pseudo Bayes factor measure were effective at model diagnosis and selection. Also, our procedure was robust against the choices of hyperparameter values.
Lastly, to investigate the performances of MCMC sampling with and without PG augmentation sampling, we considered artificial data with a sample size 800. The dataset was generated from the model given in the previous estimate issue. We implemented MCMC sampling under prior I. The PG sampling method and the MH algorithm were used to draw observations of \({\varvec{\alpha }}_1\), \({\varvec{\beta }}_1\) and \({\varvec{\varOmega }}\) from their posteriors, respectively. For the MH algorithm, we adjusted the acceptance rates between 0.3 to 0.45. Figure 2 presents the plots of auto-correlation coefficients of \(\alpha _{11}\), \(\beta _{11}\), \(\varLambda _{21}\) and \(\varGamma _{11}\) versus the number of lags under the PG sampling and MH algorithm in the first 100 lags. The autocorrelation coefficients of the samples produced by the MH algorithm decayed slowly when compared to those of the PG samples.
Table 5 presents a summary of estimates of the unknown parameters obtained by the MH algorithm and the PG sampling under prior I over 100 replications. As suggested by a referee, we also included a summary based on the thinning MCMC sampling, for which every 10th observation from 2000 samples was selected after deleting first 2000 observations. There is no obvious difference between them. The PG sampling was seemingly more reasonable, but the distinctions were negligible. Of these, the MH algorithm was the fastest, and each replicate required about 79 s. For computation, all programmes were coded in the C language and implemented on the Inter(R) Core(TM), i5-65000 processor with a 3.20-GHz CPU on the Microsoft Windows 7 operating system. All figures were plotted using the Matlab(R) software. Requests for the code can be sent to the corresponding author.
5 Household Finance Debt Data
5.1 Data Description
In this section, a small portion of household finance debt data was analyzed to illustrate the actual merits of the methodology. As stated in Introduction, started in 2011, over 30,000 households spread over 34 provinces, municipality, and autonomous regions in the mainland of China were followed up by the Survey and Research Center for China Household Finance, a nonprofit academic institute established by Research Institute of Economics and Management at Southwest University of Finance and Economics. The survey covered a series of questions to provide comprehensive information about various aspects of the household’s financial situation. In this study, we only focused on the measurements collected from Jiangsu, Zhejiang and Shanghai, the east regions of China, since they have similar economic levels. The main objective was to explore the effects of related latent and observed exogenous factors on the household finance debt, including the secured debt and unsecured debt, and assess the relationships between them. In particular, we concentrated upon the study of how the household finance literacy and family culture affected the proportion of households holding debt and the magnitude of the debt per household. To this end, we extracted eight items to conduct data analysis (see Appendix for details on the selected manifest variables). The first measurement was the ‘gross debts per household (DEB),’ the sum of the secured and unsecured debts of a household under investigation. This was a primary measure of interest in the financial survey. It indicated whether or not a household would hold the debt and if willing, how much the debt can be carried. The next three measurements, discussed by Feng et al. [10], were three questions to evaluate the fundamental financial concepts: numeracy and capability to perform calculations related to interest rates (IR), understanding of inflation (INF), and understanding of risk diversification (RD). These measurements were scaled by 0 to 1 points according to the respondent’s answers to the questions: 1 for ‘yes’ and 0 for ‘no,’ and hence, it was treated as binary. The last four measurements, according to the module of CHFS, were taken to index the family culture: the attitude toward the boy preference of a family (BP), the understanding of the children singleness (CS), the opinion on the children filial (CF), and the opinion on the status of a family in the respondent’s life (SF). According the nature of the questions, the first two measurements ‘BP’ and ‘CS,’ on scales from 0 to 2, were treated as multinomial data, while the last two measurements ‘CF’ and ‘SF,’ with a five-point scale {0,1,2,3,4}, were considered to be ordered categorical variables. Due to some uncertain factors, about 3.37% measurements were missing. We treated the missing data as missing at random (MAR) and ignorable [27]. In this setting, the specific missing mechanism that resulted in missing data was ignored. Among them, the variable DEB contained excess zeros. The proportion of zeros was about 76.81%. Thus, we treated this variable as semi-continuous. Figure 3 presents the histograms of DEB and their natural logarithms of positive values. The skewness and kurtosis of \(\ln c_i\) were 1.3755 and 3.0391, respectively, which were consistent with the assumption of the proposed model.
Moreover, motivated by the existing literature (e.g., [10, 37]), the following observed covariates were used to explain observable variation of binary and continuous components of household finance debts. These control variables were the health status (\(x_1\), 1 if excellent/good and 0 otherwise), the educational attainment (\(x_2\), 1 if completed high school and 0 otherwise), self-employed (\(x_3\), 1 if self-employed and 0 otherwise) and the number of adults (age > 16) in a family (\(x_4\), values ranging from 1 to 5 ). In this study, we only considered the observations of subjects with fully observed covariates. The total sample size \(N=4482\).
5.2 Model Formulation
In formulating our LVM for the observed variables, we first noted that the single observed variable DEB provided key information about the potentiality of a household holding financial debt. Hence, the variable DEB was grouped to form a latent variable \(\eta _i\) that could be interpreted as the ‘potentiality of holding household financial debt’. This modeling strategy was obviously different from that of Feng et al. [10], who treated DEB as direct outcome variable rather than manifest variable when grouping latent variables. Then, following a similar idea to that in [10], we grouped IR, INF and RD into a latent variable \(\xi _{i1}\), which could be interpreted as the ‘household financial literacy’. Finally, the last four measurements were grouped together to form a third latent variable \(\xi _{i2}\), interpreted as the ‘family culture.’ We treated \(\xi _{ij}(j=1,2)\) as the exogenous factors and \( \eta _i\) as the endogenous factor. To detect the possible the relationships between them, we considered the following structural equation:
where \(\varGamma _1\) and \(\varGamma _2\) are the regression coefficients used to identify the magnitudes of effects of the household financial literacy and family culture on the potentiality of holding finance debt, and \(\zeta _i\) is the unique error representing idiosyncratic part that cannot be explained by \(\xi _{ij}\). We assumed that \(\zeta _i\sim N(0, \psi _\zeta )(\psi _\zeta > 0)\). Moreover, based on the nature of problem and previous analysis, we formulated DEB into the following two-part regression model:
where \(u_i\) and \(z_i\), as mentioned above, denote the occurrence variable and the intensity variable related to the DEB, respectively; \(\alpha _{h0}(h=1,2)\) represents the intercept parameters, and \({\varvec{\gamma }}_h\) and \({\varvec{\beta }}_h (h=1,2)\), represent the regression coefficients and factor loading vectors, respectively. Since we index \(\eta _i\) through a single manifest variable \(c_i\), the factor loadings in (5.2) and (5.3) were taken with the forms of \({\varvec{\beta }}_1=(1^*,0^*,0^*)\) and \({\varvec{\beta }}_2=(\beta _{21},0^*,0^*)\), where the elements with an asterisk were treated as fixed. Furthermore, letting \({\textbf{v}}_i\)=(IR,INF,RD,BP,CS,CF,SF)\(_i\), we considered the following factor loadings matrix for \({\textbf{v}}_i\):
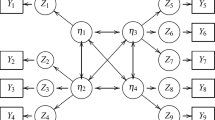
in which one and zero were treated as fixed. We adopted an orthogonal structure for \({\varvec{\varLambda }}\), which provided clear interpretations of the latent factors. According to the usual practice of SEMs, the fixed value 1.0 was also used to specify the scale of factor. Note that in the study of Feng et al. [10], the factor loadings were set as overlapping. As an illustration, a path diagram for the observed and latent variables (omitting covariates to save space) is given in Fig. 4. The estimated effects under \(M_1\) (see below) are also given in these figures.
5.3 Model Fitting and Results Analysis
We proceed with the data analysis by first fitting data to the following competing models:
These models denote different parsimonious levels on the posited model and often represent the various relevance under consideration. For example, \(M_2\) implies that the proportion of households holding debt is independent of \(\eta _i\), and the potentiality of holding debt and its variability are totally explained by the observed factors. The interpretations of \(M_2\) to \(M_5\) are similar. In particular, \(M_5\) indicates that no direct effects of financial literacy and family culture exits on the potentiality to hold finance debt, and the whole model is broken into two separated models: the conventional two-part regression model and the classic LVM with mixed data. Although other combinations of the above models are possible, our focus is mainly examining the effects of latent factors on the various aspects of the proposed model.
For model comparison, the MCMC algorithm given in Sect. 3 was implemented to calculate BF and LPML for each fit. Since the parameters involved in \(M_1\) to \(M_6\) varied with the model, we specified priors to all unknown parameters contained in the overall model. Moreover, we considered the following inputs of the priors: \(\widetilde{{\varvec{\gamma }}}_{01}=\widetilde{{\varvec{\gamma }}}_{02}={\varvec{0}}_8\), \({{\varvec{H}}}_{10}={{\varvec{H}}}_{20}=100\times {{\varvec{I}}}_8\), \(\alpha _{\epsilon 0}=\beta _{\epsilon 0}=2.0\), \({\varvec{\mu }}_0={{\varvec{0}}}_7\) and \({\varvec{\varSigma }}_0=100\times {{\varvec{I}}}_7\); \({\varvec{\varLambda }}_{0k}\) and \({\varvec{\varGamma }}_0\) were fixed at zeros, \({{\varvec{H}}}_{\delta 0k}\) and \(H_{\zeta 0}\) were set to be the identity matrices; \(\alpha _{\delta 0 k}=\alpha _{\zeta 0}=10.0\), \(\beta _{\delta 0k}=\beta _{\zeta 0}=9.0\), \(\rho _0=10.0\) and \({{\varvec{R}}}_0={{\varvec{I}}}_2\). Due to the presence of missing data, we needed to impute missing values in the posterior analysis. This problem was addressed by augmenting the missing data with latent quantities \({\varvec{\varOmega }}\), \({{\varvec{V}}}_1^*\), \({{\varvec{V}}}_2^*\) and \({\varvec{\theta }}\), and drawing them from posterior distributions. Specifically, we let \(v_{i1j, mis}\) and \(v_{2ik,mis}\) be the jth and the kth missing entries in \({\textbf{v}}_{1i}\) and \({\textbf{v}}_{2i}\), respectively, and let \(v_{1ij,mis}^*\) and \({\textbf{v}}_{2ijk,mis}^*\) be the counterparts in \({\textbf{v}}_{1i}^*\) and \({\textbf{v}}_{2i}^*\). The imputation of missing data was achieved by drawing \(v_{1ij,mis}^*\) from \(N(\mu _{1j,mis}+{\varvec{\varLambda }}_{1j,mis}^T{\varvec{\omega }}_i,\psi _{\delta j})\) and drawing \({\textbf{v}}_{2ik,mis}^*\) from \(N_4(\mu _{2j,mis}{{\varvec{1}}}_4+{\varvec{\varLambda }}_{2j,mis}^T{\varvec{\omega }}_i,{{\varvec{I}}}_4)\), where \(\mu _{1j,mis}\), \({\varvec{\varLambda }}_{1j,mis}\), \(\mu _{2j,mis}\) and \({\varvec{\varLambda }}_{2j,mis}\) are the components in \({\varvec{\mu }}_1\), \({\varvec{\varLambda }}_1\), \({\varvec{\mu }}_2\) and \({\varvec{\varLambda }}_2\) corresponding to the missing components \(v_{1ij,mis}\) and \(v_{2ij,mis}\), respectively. For computation, the adjustable parameters involved in the MH algorithm were set to guarantee that the rate of acceptance was about 0.3 under all settings. The convergence of algorithm were required for all fittings. Figure 5 presents the trace plots of the estimates of \(\gamma _{11}\), \(\gamma _{21}\), \(\psi _\epsilon \), \(\mu _1\), \(\varLambda _{22}\), \(\varPi _{11}\), \(\psi _\zeta \) and \(\varPhi _{12}\) based on three different starting values under \(M_1\). The convergence of sampling was fast. To be conservative, for all scenarios, we collected 3000 observations after removing the initial 2000 iterations to calculate BF and LPML.
Trace plots of the estimates of unknown parameters in the posterior sampling under \(M_1\): (a)\(\gamma _{11}\), (b)\(\gamma _{21}\), (c)\(\varPsi _\epsilon \), (d)\(\mu _1\), (e)\(\varLambda _{22}\), (f)\(\varGamma _{11}\), (g)\(\varPsi _\zeta \) and (h)\(\varPhi _{12}\): China household finance survey data
Again, we treated full model \(M_1\) as the reference model in the computation of BF. The linking models were defined similarly as those in the simulation study. The number of grids in [0,1] was taken as \(S=20\). For the LPML, after convergence of the algorithm, we drew \(H=100\) independent observations from \(t_4({{\varvec{0}}}, {\varvec{\varSigma }}_\omega ({\varvec{\theta }}))\) at each iteration to calculate the individual likelihood of the observed data (see(3.7)). We found that \(\log \text {BF}_{21}=10.85\), \(\log \text {BF}_{31}=7.052\), \(\log \text {BF}_{41}=14.076\), \(\log \text {BF}_{51}=122.934\), and \(\log \text {BF}_{61}= 11.396\). The estimates of LPML are in order \(-\)37685.922(\(M_1\)), \(-\)37779.965(\(M_2\)), \(-\)37800.980(\(M_3\)), \(-\)37694.254 (\(M_4\)) and \(-\)37863.836 (\(M_5\)). Examinations of LPML and BFs showed that \(M_1\) outperformed the other competing models with decisive evidence. Hence, \(M_1\) is selected. It was concluded from the model comparison results that the inclusion of latent factors in two-part model significantly improved model fits when compared to the ordinary regression model. It also indicated that strong dependence of exogenous factors on the endogenous factors existed.
Table 6 presents the resulting estimates of the unknown parametersFootnote 1 associated with their corresponding standard deviation estimates under \(M_1\).
Examination of Table 6 reveals the following facts: (i) The observable explanatory variables (covariates) had substantial influences on the household finance debts. First, the estimates of intercept parameter \(\widehat{\alpha }_{10}=-2.571\) associated with SD=0.160 implied that the baseline level of odds of holding-finance-debt households in these areas was less than 1 and equaled approximately to 0.0765 when other covariates were zeros. The average amount of debts held in this case was about CNY 16, 848, according to the estimate \(\widehat{\alpha }_{20}=9.732\). Second, for the healthy status, the estimates of regression coefficients \(\widehat{\gamma }_{11}\) and \(\widehat{\gamma }_{21}\) yielded opposite conclusions. There was a negative association between the group being in a good health and the probability of holding debt. The odds of holding debt within an good/excellent heath condition is about 0.918 times that with less heathy conditions. This finding was also unveiled by Feng et al. [10] when assessing the financial risk using all datasets. However, among the households of holding debt, the amount of debt being held was positively correlated with the heathy status, which was in contrast with the results of [10]. The difference of the average amount of debts held between two kinds of households was about CNY 1.740. This indicated that in households with less patients, the heads were more willing to holding more secured and nonsecured debt. Third, for the educational attainment, the estimates \(\widehat{\gamma }_{21}=-0.519\) associated with SD=0.088 and \(\widehat{\gamma }_{31}=-0.004\) associated with SD=0.112 indicated that there were negative effects of the educational levels on the probability of indebted households and the amount of debt held. These results were also not consistent with those of [10]. The underlying reason was perhaps that we only focused on the east economic developed areas, where the economic level are relatively high with more higher educational attainment. Fourth, as for the employment, the conclusion were similar to Feng et al. [10], but the magnitude of effects were different. A self-employed household head was more likely to hold debt and also tended to carry a large amount of debts. Finally, it follows from \(\widehat{\gamma }_{41}=0.338\) and \(\widehat{\gamma }_{42}=0.178\) that the households with larger number of adults and children were more likely to hold debts. These results were consistent with the findings given by Feng et al. [10]. (ii) For the latent factors, since we related \(\eta _i\) to the proportion of the indebted households by fixing \(\beta _{11}=1.0\), the estimate \(\widehat{\beta }_{21}=0.757\) indicated that a one unit change in the level of potentiality of holding debts would lead to increases of the debts about CNY 2.1319. Furthermore, examination of \(\widehat{\varLambda }_{jk}\) showed that there were positive associations with the probabilities of the occurrences of categories except \(\widehat{\varLambda }_{73}=-0.032\). Recall that we scaled the questions of opinion on the status of family such that 0 was very important and 5 was very unimportant. Thus, the negative value of \(\widehat{\varLambda }_{73}\) suggested that increasing the levels of family culture would have a positive effect on the SF. (iii) The estimated structural equation that addressed the relations of the potentiality to holding/carrying for debt with household finance literacy and family culture was our main consideration. It follows from \(\widehat{\varGamma }_{11}=0.415\) and \(\widehat{\varGamma }_{12}=0.185\) that both the household financial literacy and family culture had positive effects on the level of potentiality of holding household financial debt. Increasing the household finance literacy and family culture per unit increased by an average of 0.6 in the magnitude of the level of debts held in these economic developed areas. This reflected that with more household finance literacy, insights to the national economic regulations and finance knowledge to the economic leverage and finance tools, the greater the debts that a household would hold. (iv) However, based on the estimate of correlation coefficient \(\widehat{\varPhi }_{12}=-0.225\), it was concluded that the variations of financial literacy and family culture are opposite. This may have been attributed to the Chinese traditional family culture in the east regions of China.
Furthermore, to assess the adequacy of the normality on \(z_i\), \(\zeta _i\), \(\eta _i\) and \(\xi _{ij}\), we checked the estimated residuals \(\widehat{\epsilon }_i=z_i-\widehat{\alpha }_{20}-\widehat{{\varvec{\gamma }}}_2^T{\textbf{x}}_i-\widehat{{\varvec{\beta }}}_2^T\widehat{{\varvec{\omega }}}_i\), \(\widehat{\zeta }_i=\widehat{\eta }_i-\widehat{\varGamma }_1\widehat{\xi }_{i1}-\widehat{\varGamma }_2^T\widehat{\xi }_{i2}\), as well as the scores of latent factors \(\widehat{\xi }_{i1}\), \(\widehat{\xi }_{i2}\), where \(\widehat{\epsilon }_i\), \(\widehat{\zeta }_i\), \(\widehat{\xi }_{i1}\) and \(\widehat{\xi }_{i2}\) were the Bayes estimates. We examined their Q-Q plots (not presented to save spaces) and found that the results were more consistent with model convenience. Moreover, the plots of \((\widehat{\xi }_{ij}\), \(\widehat{\zeta }_i)(j=1,2)\) lied within two parallel horizontal lines that were not widely separated apart and centered at zero, which indicated a reasonably good fit of the structural equation.
6 Discussion
In this study, we proposed a general two-part latent variable model to analyze household finance debt data. Multiple factors were included to interpret extra variation arising from the absence of explanatory variables, and the structural equation was used to investigate the impacts of finance literacy and family culture on the potentiality of a household holding finance debt. Although there is a body of work on using latent variables to representing various relevances under consideration (see [10] for a brief review), our development was obviously different from the existing literature for analyzing the household financial debt. We identify the household debts as the potentiality of holding debt rather than dependent outcomes. In fact, the proportion of indebted households and the magnitude of debt being held reflected the degree of economic activity, the level of resident’s life standard, and the knowledge about the national macro-economic situations in a country/area, which ultimately could be synthesized to determine the potentiality of a household in holding finance debt. This treatment also allows one to assess the impact of other latent quantities such as financial literacy and family culture, as discussed in this paper, on the potential of paying back debt or investment aspirations. Consequently, our method provides a novel perspective in modeling the household finance data.
In this methodology, we developed a Bayesian procedure to carry out statistical inferences. In particular, PG augmentation approach was adapted to facilitate the posterior sampling. We illustrated the merits of the propose methodologies via empirical results. Extensions of the current development to analyze more complex situations such as hierarchically structured data and/or two levels of two-part latent variable model require more elaborate design and are a subject of further study.
An important practical matter is related to the number of chains. Recommendations in the literature related to the number of chains have been conflicting, ranging from many short chains, to several long ones, to one very long. It is now generally agreed that running many short chains, motivated by desire to obtain independent samples, is misguided unless there is some special needing independent sample [17]. Furthermore, independent samples are not required for ergodic averaging. Further discussions on thinning MCMC can refer to Geyer [17] and Owen [35].
Beyond estimation, one important issue related to statistical inference is on testing various hypotheses about the model adequacy and assessing model fits. Within the Bayesian paradigm, this problem is commonly solved via comparing marginal likelihoods of the observed data across competing models. The Bayes factor and/or prediction-based measures can be used to assess the goodness of fit of the posited models by specifying one as the basic saturated model. A simple and more convenient alternative without involving the basic saturated model is the posterior predictive p-values (PP p-values, [30]). It has been shown that (see [14]) this approach is conceptually and computationally simple and is useful in model-checking for a wide varieties of complicated situations. However, it should be noted that the PP p-value is only useful for goodness-of-fit assessment of a single model. It is not suitable for comparing different models. Moreover, it may show good fit for some inappropriate models, due to the problem of using the data twice. Other common model checking methods in data analysis, including residual analysis and tests of outliers, can be incorporated in the Bayesian analysis.
Notes
The summary of threshold and intercept parameters related to manifest variables is omitted in Table 5 for presentation clarity.
References
Agresti, A.: An Introduction to Categorical Data Analysis, 2nd edn. Wiley, Hoboken (2007)
Berger, J.O.: Statistical Decision Theory and Bayesian Analysis. Springer, New York (1985)
Bernheim, D.: Do households appreciate their financial vulnerabilities? An analysis of actions, perceptions, and public policy. Tax Policy Econ. Growth 3, 11–13 (1995)
Bollen, K.A.: Structural Equations with Latent Variables. Wiley, New York (1989)
Brown, S., Ghosh, P., Su, L., Taylor, K.: Modelling household finances: a bayesian approach to a multivariate two-part model. J. Empir. Financ. 33, 190–207 (2015)
Browning, M., Lusardi, A.: Household saving: micro theories and micro facts. J. Econ. Lit. 34(4), 1797–1855 (1996)
Chow, S.M., Tang, N.S., Yuan, Y., Song, X.Y., Zhu, H.T.: Bayesian estimation of semiparametric nonlinear dynamic factor analysis models using the Dirichlet prior. Br. J. Math. Stat. Psychol. 64, 69–106 (2011)
Cragg, J.G.: Some statistical models for limited dependent variables with application to the demand for durable goods. Econometrica 39(5), 829–844 (1971)
Duan, N., Manning, W.G., Morris, C.N., Newhouse, J.P.: A Comparison of alternative models for the demand for medical Care. J. Bus. Econ. Stat. 1(2), 115–126 (1983)
Feng, X.N., Lu, B., Song, X.Y., Ma, S.: Financial literacy and household finances: a Bayesian two-part latent variable modeling approach. J. Empir. Financ. 51, 119–137 (2019)
Geisser, S., Eddy, W.: A predictive approach to model selection. J. Am. Stat. Assoc. 74, 1537–1160 (1979)
Gelfand, A.E., Smith, A.F.M.: Sampling-based approaches to calculating marginal densities. J. Am. Stat. Assoc. 85(410), 398–409 (1990)
Gelman, A., Meng, X.L.: Simulating normalizing constants: from importance sampling to bridge sampling to path sampling. Stat. Sci. 13, 163–185 (1998)
Gelman, A., Meng, X.L., Stern, H.: Posterior predictive assessment of model fitness via realized discrepancies. Stat. Sin. 6, 733–759 (1996)
Gelman, A., Rubin, D.B.: Inference from iterative simulation using multiple sequences (with discussion). Stat. Sci. 7(4), 457–511 (1992)
Geman, S., Geman, D.: Stochastic relaxation, Gibbs distribution, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-6(6), 721–741 (1984)
Geyer, C.J.: Practical Markov chain Monte Carlo. Stat. Sci. 7(4), 473–511 (1992)
Gilks, W.R., Wild, P.: Adaptive rejection sampling for Gibbs sampling. Appl. Stat. 41, 337–348 (1992)
Hastings, W.K.: Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970)
Jöreskog, K.G.: A general approach to conrmatory maximum likelihood factor analysis. Psychometrika 34, 183–202 (1969)
Kass, R.E., Raftery, A.E.: Bayes factors. J. Am. Stat. Assoc. 90(430), 773–795 (1995)
Kim, Y.K., Muthén, B.O.: Two-part factor mixture modeling: application to an aggressive behavior measurement instrument. Struct. Equ. Model. 16(4), 602–624 (2009)
Lee, S.Y.: Structural Equation Modeling: A Bayesian Approach. Wiley, New York (2007)
Lee, S.Y., Xia, Y.M.: A robust bayesian approach for structural equation models with missing data. Psychometrika 73(3), 343–364 (2008)
Liu, L., Strawderman, R.L., Cowen, M.E., Shih, Y.C.T.: A flexible two-part random effects model for correlated medical costs. J. Health Econ. 29(1), 110–123 (2010)
Liu, L., Strawderman, R.L., Johnson, B., O’Quigley, J.M.: Analyzing repeated measures semicontinuous data, with application to an alcohol dependence study. Stat. Methods Med. Res. 25(1), 1–33 (2016)
Little, R.J.A., Rubin, D.B.: Statistical Analysis with Missing Data, 2nd edn. Wiley, New York (2002)
Lusardi, A., Mitchell, O.S.: Baby boomer retirement security: the roles of planning, financial literacy, and housing wealth. Monetary Econ. 42, 35–44 (2007)
Manning, W.G., et al.: A two-part model of the demand for medical care: preliminary results from the health insurance experiment. In: van der Gaag, J., Perlman, M. (eds.) Health, Economics, and Health Economics, p. 103C104. North-Holland, Amsterdam (1981)
Meng, X.L.: Posterior predictive p-values. Ann. Stat. 22, 1142–1160 (1994)
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., Teller, E.: Equations of state calculations by fast computing machine. J. Chem. Phys. 21, 1087–1091 (1953)
Mukhopadhyay, S., Gelfand, A.E.: Dirichlet process mixed generalized linear models. J. Am. Stat. Assoc. 92(438), 633–639 (1997)
Neelon, B., Zhu, L., Neelon, S.E.B.: Bayesian two-part spatial models for semicontinuous data with application to emergency department expenditures. Biostatistics 16(3), 465–479 (2015)
Olsen, M.K., Schafer, J.L.: A two-part random-effects model for semicontinuous longitudinal data. J. Am. Stat. Assoc. 96(454), 730–745 (2001)
Owen, A.B.: Statistically efficient thinning of a Markov chain sampler. J. Comput. Graph. Stat. (2017). https://doi.org/10.1080/10618600.2017.1336446
Polson, N.G., Scott, J.G., Windle, J.: Bayesian inference for logistic models using PlyaCGamma latent variables. J. Am. Stat. Assoc. 108(504), 1339–1349 (2013)
Rooij, M.V., Lusardi, A., Alessie, R.: Financial literacy and stock market participation. J. Financ. Econ. 101(2), 449–472 (2011)
Shi, J.Q., Lee, S.Y.: Bayesian sampling-based approach for factor analysis model with continuous and polytomous data. Br. J. Math. Stat. Psychol. 51(2), 233–252 (1998)
Smith, V.A., Neelon, B., Preisser, J.S., Maciejewski, L.: A marginalized two-part model for semicontinuous data. Stat. Med. 33(28), 4891–4903 (2015)
Schneider, S., Stone, A.A.: Distinguishing between frequency and intensity of healthrelated symptoms from diary assessments. J. Psychosom. Res. 77(3), 205C212 (2014)
Song, X.Y., Xia, Y.M., Lee, S.Y.: Bayesian semiparametric analysis of structural equation models with mixed continuous and unordered categorical variables. Stat. Med. 28(17), 2253–2276 (2010)
Tooze, J.A., Grunwald, J.K., Jones, R.H.: Analysis of repeated measures data with clumping at zero. Stat. Methods Med. Res. 11(4), 341–355 (2002)
Walker, S.G.: Sampling the Dirichlet mixture model with slices. Commun. Stat. Simul. Comput. 36(1), 45–54 (2007)
Wang, X.Q., Feng, X.N., Song, X.Y.: Joint analysis of semicontinuous data with latent variables. Comput. Stat. Data Anal. 151, 107005 (2020)
Xia, Y.M., Gou, J.W.: Bayesian semiparametric analysis for latent variable models with mixed continuous and ordinal outcomes. J. Korean Stat. Soc. 45(3), 451–465 (2016)
Xia, Y.M., Lu, B., Tang, N.S.: Inference on two-part latent variable analysis model with multivariate longitudinal data. Struct. Equ. Model. A Multidiscipl. J. 26(5), 685–709 (2019)
Zhu, H.T., Lee, S.Y.: A Bayesian analysis of finite mixtures in the LISREL model. Psychometrika 66(1), 133–152 (2001)
Acknowledgements
The research described herein was fully supported by National Nature Science Foundation of China (No. 11471161) and the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (No. 15KJB110010). The authors are thankful to the Editor and two anonymous reviewers for the valuable comments that improved the paper significantly, and they are grateful to the CHFS, the Institute of China Household Finance Survey for providing the household finance data.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest to this work.
Appendix
Appendix
1.1 Appendix I. Full Conditionals in MCMC Sampling
In this section, we present the technical details on the full conditionals involved in the MCMC sampling. Note that given \({\varvec{V}}_1^*\), \({\varvec{V}}_2^*\), \({\varvec{\varOmega }}\), \({\varvec{U}}\) and \({\varvec{Z}}\), Equations (2.3), (2.6) and (2.7) reduce into ordinary regression models. The full conditionals distributions (e) \(p(\widetilde{{\varvec{\gamma }}}_2,{\varvec{\varPsi }}_\epsilon |{\varvec{\varOmega }},{\varvec{U}},{{\varvec{Z}}})\), (f) \(p({\varvec{\mu }}|{\varvec{\varLambda }},{\varvec{\varPsi }}_\delta ,{\varvec{\varOmega }},{{{\varvec{V}}}}_1^*,{{{\varvec{V}}}}_2^*)\), (g) \(p({\varvec{\varLambda }},{\varvec{\varPsi }}_\delta |{\varvec{\mu }},{\varvec{\varOmega }}, V)\), (h) \(p({\varvec{\varPi }},{\varvec{\varPsi }}_{\zeta }|{\varvec{\varOmega }})\) and (i) \(p({\varvec{\varPhi }}|{\varvec{\varOmega }}_2)\) are all the standard distributions, which can be obtained via a standard procedure in the regression analysis (see for example, [23]). Furthermore, the conditional distribution (c) \(p({\varvec{\alpha }},{{\varvec{V}}}_1^*|{\varvec{\theta }},{\varvec{U}}^*,{\varvec{\varOmega }},{\varvec{V}})\) can be obtained by following the routine in [45]. We omit the technical detail on these distributions and only focus on the full conditionals of \({\varvec{\varOmega }}\), \(\{{\varvec{U}}^*,\widetilde{{\varvec{\gamma }}}_1\}\) and \({\varvec{V}}_2^*\).
(a) \(p({\varvec{\varOmega }}|{\varvec{\theta }},{U}^*,{V}_1^*,{V}_2^*,{U},{Z})\)
Let \({\textbf{v}}_i^{**}=({\textbf{v}}_{i1}^*,{\textbf{v}}_{i21}^{*T},\cdots ,{\textbf{v}}_{i2,s_2}^{*T})^T\) be the \((s_1+Ks_2)\times 1\)-dimensional vector and let \(\textbf{C}=diag\{{\varvec{I}}_{s_1},{\varvec{1}}_L,\cdots ,{\varvec{1}}_L\}\) and \({\varvec{\varPsi }}_\delta ^*=diag\{{\varvec{\varPsi }}_{\delta 1},\psi _{\delta s_1+1}{\textbf{I}}_L,\cdots ,\psi _{\delta p}{\textbf{I}}_L\} \) be the \((s_1+s_2\times K)\) diagonal matrices, where \(\textbf{1}_L\) is the \(L\times 1\) vector with all elements being unity. We write Equation (2.4) associated with (2.6) and (2.7) as
where \({\varvec{\delta }}_i^*\sim N({\varvec{0}},{\varvec{\varPsi }}_\delta ^*)\).
It follows from Eqs. (2.2)–(2.5) that
Let \({\varvec{\kappa }}_i^*=(\kappa _{i1}/u_{i1}^*,\cdots ,\kappa _{ir}/u_{ir}^*)^T\), \({\varvec{\varPsi }}_{ui}^*=diag\{u_{i1},\cdots ,u_{ir}^*\}\) and \({\varvec{\varPsi }}_{\epsilon i}^*=diag\{u_{i1}/\psi _{\epsilon 1},\) \(\cdots ,u_{ir}/\psi _{\epsilon r}\}\). By some algebra, it can be shown that
where
with
(b) \(p({U}^*,\widetilde{{\varvec{\gamma }}}_1|{\varvec{\varOmega }},{U})\)
We update \({\varvec{U}}^*\) and \(\widetilde{{\varvec{\gamma }}}_1\) by drawing \({\varvec{U}}^*\) from \(p({\varvec{U}}^*|\widetilde{{\varvec{\gamma }}}_1,{\varvec{\varOmega }},{\varvec{U}})\) and \(\widetilde{{\varvec{\gamma }}}_1\) from \(p(\widetilde{{\varvec{\gamma }}}_1|{{\varvec{U}}}^*,{\varvec{\varOmega }},{\varvec{U}})\). The former is independent of \({\varvec{U}}\).
By Model (2.10), it can be shown that
where \(\text {PG}(1,a)\) is the PG distribution, through an exponential tilting of the PG(1,0) density with parameter a. Hence, the draw of \({\varvec{U}}^*\) can be achieved by simulating \(u_{ij}^*\) in a single-component way. Note that there is no standard form available for this target distribution. We adopt the routine in [36] and draw \(u_{ij}^*\) via rejection-acceptance sampling method.
Given \({\varvec{U}}\), \({\varvec{U}}^*\) and \({\varvec{\varOmega }}\), Equation (2.10) can be considered to be an ordinary linear regression model \(\kappa _{ij}^*=\widetilde{{\varvec{\gamma }}}_{1j}^T{\varvec{\omega }}_{ui}^*+\epsilon _{ij}^*\), where \(\kappa _{ij}^*\) is given in (i), and \(\epsilon _{ij}\)s are independently distributed with \(N(0,1/u_{ij}^*)\). This indicates that the conditional distribution \(p(\widetilde{{\varvec{\gamma }}}_1|{{\varvec{U}}}^*,{\varvec{\varOmega }},{{\varvec{U}}})\) can be obtained via standard Bayesian analysis procedure for the linear regression model.
(c) \(p({{\varvec{V}}}^*_2|{\varvec{\theta }},{\varvec{\varOmega }},{{\varvec{V}}})\)
Recall that \({\varvec{\nu }}_k=\textbf{1}_L\) and \(\textbf{R}_k={\textbf{I}}_L\). It can be shown that
where \(\otimes \) denotes the Kronecker product. If \(v_{2ij}=k=0\), then
which results in a truncate normal distribution for \({\textbf{v}}_{2ij}^*\). If \(v_{2ij}=k\ne 0\), then
where \(a\vee b\) means the maximum of a and b.
1.2 Appendix II. Choices of Hyperparameters
The inputs of hyperparameters involved in the simulation study are briefly discussed here.
For BAY I, we assigned normal prior N(0, 100) to the components in \(\tilde{{\varvec{\gamma }}}_{1j}\), \({\varvec{\varLambda }}\) and \({\varvec{\varGamma }}\). Although these were proper probability distributions, we might expect to have minimal effects on the analysis since they had standard deviation 10. This guaranteed that the realizations of these parameters lie in the symmetric interval \([-30,30]\) with a probability about 99.74%. Hence, such priors could be regarded as our noninformative beliefs on these parameters. For the variance parameters, we assigned inverse gamma priors IG(0.001, 0.001) to \(\psi _\epsilon \), \(\psi _{\delta k}\) and \(\psi _\zeta \). The inverses of the variance components (the precisions) all had prior deviations 1000. This ensured that their distributions were inflated enough. For the covariance matrix, the inverse wishart distribution \(IW_2(1,100\times {\textbf{I}}_2\) produced a nonformation prior for \({\varvec{\varPhi }}\).
For BAY II, the normal distributions with means equal to the true population values and variances equal to unity were assigned to the components in \(\tilde{{\varvec{\gamma }}}_{1j}\), \({\varvec{\varLambda }}\) and \({\varvec{\varGamma }}\). This can be considered to be informative priors since they delivered the information of locations consistent with true values. Similarly, the inverse gamma priors IG(9.0, 8.0) for \(\psi _\epsilon \), \(\psi _{\delta j}\) and \(\psi _\zeta \) yield means 1.0 and variances 0.143 and the inverse wishart \(IW_2(10,7\times {\textbf{I}}_2)\) yielded the mean \({\varvec{I}}_2\) for \({\varvec{\varPhi }}^{-1}\).
1.3 Appendix III. Manifest Variables in Household Finance Debts
The following original questions were designed following the module in HRS 2004 [28]:
Q1. Suppose you have CNY100 in a savings account and the interest rate is 4% per year. After one year, how much do you think you would have in the account if you left the money to grow? (i) Less than CNY104 (ii) Exactly CNY104 (iii) More than CNY104 (iv) Do not know.
Q2. Imagine that the interest rate on your savings account is 5% per year and the inflation rate is 3% per year. After one year, would you be able to buy(i) More than (ii) Exactly the same as (iii)Less than (iv) Do not know, today with the money in this account?
Q3. In general, which one is riskier, a single company’s stock or a stock mutual fund? (i) Stock (ii) Mutual fund (iii) Do not know stock (iv) Do not know mutual fund (v) Do not know stock and mutual fund.
Q4. Would you prefer having a boy or girl? (i) Boy (ii) Girl (iii) It does not matter.
Q5. What is your opinion on the children singleness? (i) Accepted (ii) Unaccepted (iii) Does not matter.
Q6. Do you agree that children should be filial regardless of their parents’ behavior? (i) Strongly disagreed (ii) Less agreed (iii) It does not matter (iv) More agreed (v) Strongly agreed.
Q7. How important is the family in your life? (i) Very important (ii) Important (iii) It does not matter (iv) Unimportant (v) Very unimportant.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xiong, SC., Xia, YM. & Lu, B. Bayesian Analysis of Two-Part Latent Variable Model with Mixed Data. Commun. Math. Stat. (2023). https://doi.org/10.1007/s40304-023-00359-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40304-023-00359-1