The kth Power Expectile Estimation and Testing

Abstract

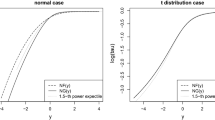
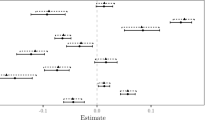
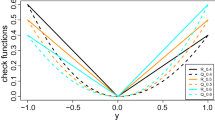
This paper develops the theory of the kth power expectile estimation and considers its relevant hypothesis tests for coefficients of linear regression models. We prove that the asymptotic covariance matrix of kth power expectile regression converges to that of quantile regression as k converges to one and hence promise a moment estimator of asymptotic matrix of quantile regression. The kth power expectile regression is then utilized to test for homoskedasticity and conditional symmetry of the data. Detailed comparisons of the local power among the kth power expectile regression tests, the quantile regression test, and the expectile regression test have been provided. When the underlying distribution is not standard normal, results show that the optimal k are often larger than 1 and smaller than 2, which suggests the general kth power expectile regression is necessary. Finally, the methods are illustrated by a real example.

Appendix A: The Proofs of Main Results

Proof of Theorem 2.2

Denote the kth power expectile of u by $\delta (\tau )$, i.e., $\delta (\tau )=\text{ argmin}_{l}E(Q_{\tau }(u-l)-Q_{\tau }(u))$. The first-order condition for this minimization problem shows that $\delta (\tau )$ is the solution to

$$\begin{aligned} \frac{1-\tau }{\tau }=\frac{\int _{\delta (\tau )}^{\infty } (x-\delta (\tau ))^{k-1}{\text {d}}F_{u}(x)}{\int _{-\infty }^{\delta (\tau )}(\delta (\tau )-x)^{k-1}{\text {d}}F_{u}(x)}. \end{aligned}$$

(7.1)

The equation (7.1) has a unique solution according to Theorem 1 in Jiang et al. [27] and can be rewritten as

$$\begin{aligned} \frac{1-(1-\tau )}{1-\tau }=\frac{\int _{-\delta (\tau )}^{\infty } (x-(-\delta (\tau )))^{k-1}{\text {d}}F_{u}(x)}{\int _{-\infty }^{-\delta (\tau )}(-\delta (\tau )-x)^{k-1}{\text {d}}F_{u}(x)}. \end{aligned}$$

So the solution uniqueness deduces $\delta (\tau )=-\delta (1-\tau )$. Similarly, for the regression case, ${\tilde{\beta }}(k, \tau )$ satisfies equation

$$\begin{aligned} E((-1)^{1-I(y-x'{\tilde{\beta }}(k, \tau )<0)}x|y-x'{\tilde{\beta }}(k, \tau )|^{k-1}|\tau -I(y-x'{\tilde{\beta }}(k, \tau )<0)|)=0.\qquad \end{aligned}$$

(7.2)

The item (iii) of Theorem 1 in Jiang et al. [27] implies that

$$\begin{aligned} y-x'{\tilde{\beta }}(k, \tau )= & {} u+x'\beta _{0}-x'{\tilde{\beta }}(k, \tau )=u-\delta (\tau )\\= & {} u+\delta (1-\tau )=u+x'{\tilde{\beta }}(k, 1-\tau )-x'\beta _{0}\\= & {} y-x'(2\beta _{0}-{\tilde{\beta }}(k, 1-\tau )). \end{aligned}$$

So, the left-hand side of (7.2) is equal to

$$\begin{aligned}&E((-1)^{1-I(y-x'(2\beta _{0}-{\tilde{\beta }}(k, 1-\tau ))<0)} x|y-x'(2\beta _{0}-{\tilde{\beta }}(k, 1-\tau ))|^{k-1}\\&\quad \cdot |\tau -I(y-x'(2\beta _{0}-{\tilde{\beta }}(k, 1-\tau ))<0)|). \end{aligned}$$

The solution uniqueness makes sure ${\tilde{\beta }}(k, \tau )+{\tilde{\beta }}(k, 1-\tau )=2\beta _{0}$. $\square$

Proof of Theorem 3.9

We first need two lemmas. $\square$

Lemma 7.1

If Conditions 3.1–3.2 are satisfied, for a compact set ${\mathcal {B}}_{1}$, we have that

$$\begin{aligned} \sup _{b\in {\mathcal {B}}_{1}}\Bigg |\frac{1}{T}\sum _{t=1}^\mathrm{T} Q_{\tau ,k}(y_{t}-x'_{t}b)-\frac{1}{T}\sum _{t=1}^\mathrm{T}E(Q_{\tau ,k}(y_{t}-x'_{t}b))\Bigg | {\mathop {\longrightarrow }\limits ^{\textit{a.s.}}}0, \text{ as }\ n\rightarrow \infty . \end{aligned}$$

Lemma 7.2

If Conditions 3.1–3.3 and 3.5 or Conditions 3.1–3.3 and 3.5$'$ are satisfied, $\frac{1}{T}\sum _{t=1}^\mathrm{T}E(Q_{\tau ,k}(y_{t}-x'_{t}b))$ has unique global minimum ${\tilde{\beta }}(k,\tau )$.

The existence and uniqueness of ${\tilde{\beta }}(k,\tau )$ in Theorem 3.9 are obtained using Lemma 7.2. As Condition 3.1 implies Assumption B. 1 and Assumption B.1.i in Bates and White [5], using their Theorem 2.2, we obtain the existence of ${\hat{\beta }}(k,\tau )$. Furthermore, Lemmas 7.1 and 7.2 show that Assumption B.1.ii and Assumption B.1.iii in Theorem 2.2 of Bates and White [5] are satisfied, hence

$$\begin{aligned} {\hat{\beta }}(k,\tau ){\mathop {\longrightarrow }\limits ^{\textit{a.s.}}}{\tilde{\beta }}(k,\tau )\ \text{ as } \ T\rightarrow \infty . \end{aligned}$$

(7.3)

The following is based on the classical Glivenco–Cantelli argument. Let $\varepsilon$ be any positive constant, and $n\in N$, and pick out $n+1$ $\tau$-values by continuity $\tau _{l}=\tau _{0}\le \tau _{1}\le \ldots \le \tau _{n}=\tau _{h}$, which makes sure that $\max _{1\le i\le n}\{|\tau _{i}-\tau _{i-1}|\}<c_{1}$. By the continuity of ${\tilde{\beta }}(k,\tau )$, we can find $\tau ^{*}_{i}$ and $\tau _{*i}$ such that ${\tilde{\beta }}(k,\tau ^{*}_{i})=\sup _{\tau \in [\tau _{i-1},\tau _{i}]}\{{\tilde{\beta }}(k,\tau )\}$ and ${\tilde{\beta }}(k,\tau _{*i})=\inf _{\tau \in [\tau _{i-1},\tau _{i}]}\{{\tilde{\beta }}(k,\tau )\}$. For $\tau \in [\tau _{i-1},\tau _{i}]$, we have that

$$\begin{aligned} |{\hat{\beta }}(k,\tau )-{\tilde{\beta }}(k,\tau )|\le & {} |{\hat{\beta }} (k,\tau ^{*}_{i})-{\tilde{\beta }}(k,\tau _{*i})|\\\le & {} |{\hat{\beta }}(k,\tau ^{*}_{i})-{\tilde{\beta }}(k,\tau ^{*}_{i})| +|{\tilde{\beta }}(k,\tau ^{*}_{i})-{\tilde{\beta }}(k,\tau _{*i})|. \end{aligned}$$

So, using (i) of Condition 3.4,

$$\begin{aligned} \sup _{\tau \in [\tau _{l}, \tau _{h}]}|{\hat{\beta }}(k,\tau ) -{\tilde{\beta }}(k,\tau )|\le & {} \max _{1\le i\le n}|{\hat{\beta }}(k,\tau ^{*}_{i})-{\tilde{\beta }}(k,\tau ^{*}_{i})|+C_{1}c_{1}, \end{aligned}$$

where the second term in the right-hand side is due to the uniform continuity of ${\tilde{\beta }}(k, \tau )$ with respect to $\tau$ for fixed k. By (7.3), for any $n\in N$,

$$\begin{aligned} \limsup _{T\rightarrow \infty }\sup _{\tau \in [\tau _{l}, \tau _{h}]}\Vert {\hat{\beta }}(k,\tau )-{\tilde{\beta }}(k,\tau )\Vert\le & {} \limsup _{T\rightarrow \infty }\max _{1\le i\le n}|{\hat{\beta }}(k,\tau ^{*}_{i})-{\tilde{\beta }}(k,\tau ^{*}_{i})|+C_{1}c_{1}\\= & {} C_{1}c_{1}\ \ \text{ a.s. } \end{aligned}$$

The arbitrariness of $c_{1}$ deduces that

$$\begin{aligned} \sup _{\tau \in [\tau _{l}, \tau _{h}]}\Vert {\hat{\beta }}(k,\tau )-{\tilde{\beta }}(k,\tau ) \Vert {\mathop {\longrightarrow }\limits ^{\textit{a.s.}}}0\ \text{ as } \ T\rightarrow \infty \ \text{ for } \text{ fixed }\ k. \end{aligned}$$

Using the same argument as the above and (ii) of Condition 3.4, we can also prove that

$$\begin{aligned} \sup _{k\in K}\Vert {\hat{\beta }}(k,\tau )-{\tilde{\beta }}(k,\tau ) \Vert {\mathop {\longrightarrow }\limits ^{\textit{a.s.}}}0\ \text{ as } \ T\rightarrow \infty \ \text{ for } \text{ fixed }\ \tau . \end{aligned}$$

The proof is completed. $\square$

Proof of Theorem 3.17

We only present the proof for the case $n=1$, as the argument for the case $n>1$ is similar. We first focus on the case $\zeta =0$ and consider the minimum ${\tilde{\beta }}(\tau )$ of $E(Q_{\tau , k}(y_{t}-x'_{t}b))$. Noting, when $\zeta =0$, Assumptions 3.10, 3.12, 3.13, 3.14 and 3.14$'$ imply Assumptions A1, A2, A3, A5 and A5$'$ the existence and uniqueness of ${\tilde{\beta }}(\tau )$ are established by Lemma 7.2. There exist constants $c_{1}$ and $c_{2}$ such that $Q_{\tau , k}(y_{t}-x'_{t}b)\le |z_{t}|^{k}(c_{1}+c_{2}|b|^{k}).$ Combining this and Assumptions 3.11 and 3.12, using Lemma A1 of Newey [36] yields that

$$\begin{aligned} \sup _{b\in {\mathcal {B}}_{2}}|(1/T)\sum ^{T}_{t=1}Q_{\tau , k}(y_{t}-x'_{t}b)-E(Q_{\tau , k}(y_{t}-x'_{t}b))|{\mathop {\rightarrow }\limits ^{\textit{P}}}0, \end{aligned}$$

where ${\mathcal {B}}_{2}$ is a bounded open set containing ${\tilde{\beta }}(\tau )$. So Lemma A in Newey and Powell [37] makes sure ${\hat{\beta }}(\tau )=\text{ argmin}_{R^{p}}((1/T)\sum ^{T}_{t=1}Q_{\tau , k}(y_{t}-x'_{t}b))$ exists with probability approaching one and ${\hat{\beta }}(\tau ){\mathop {\rightarrow }\limits ^{\textit{P}}}{\tilde{\beta }}(\tau )$.

We then provide the proof of the asymptotic normality. Let $E_{T}(\cdot ):=E(\cdot |\xi _{T})$. By the arguments similar to those in the proof of Theorem 3.9, we write $Q_{\tau , k}(\cdot )$ as $Q_{\tau }(\cdot )$ and have that $E_{T}(Q_{\tau }(y-x'\beta ))$ is twice continuously differentiable in $\beta$ for large enough T. Moreover,

$$\begin{aligned} \lambda _{T}(\beta )= & {} \partial E_{T}(Q_{\tau }(y-x'\beta ))/\partial \beta =E_{T}(g(\beta )),\ g(\beta )=-\varphi _{\tau }(y-x'\beta )x\\ \partial \lambda _{T}(\beta )/\partial \beta= & {} \partial ^{2}E_{T} (Q_{\tau }(y-x'\beta ))/\partial \beta \partial \beta ' \\= & {} k(k-1)E_{T}(xx'|\tau -I(y<x'\beta )||y-x'\beta |^{k-2}). \end{aligned}$$

By the continuity of $Q_{\tau }(y-x'\beta )$ in $\beta$, the continuity of $f(y|x,\xi )$ in $\xi$, and Assumption 3.12, the dominated convergence theorem makes sure that $E_{T}(Q_{\tau }(y-x'\beta ))$ converges uniformly to $E(Q_{\tau }(y-x'\beta ))$ on any compact neighborhood M of ${\tilde{\beta }}(\tau )$. We, therefore, show that there is a sequence ${\tilde{\beta }}_{T}(\tau )$ that minimizes $E_{T}(Q_{\tau }(y-x'\beta ))$ on M such that $\lim _{T\rightarrow \infty }{\tilde{\beta }}_{T}(\tau )={\tilde{\beta }}(\tau )$, and that for large enough T,

$$\begin{aligned} 0=\lambda _{T}({\tilde{\beta }}_{T}(\tau ))=E_{T}(g({\tilde{\beta }}_{T}(\tau ))). \end{aligned}$$

(7.4)

Using the continuity of $f(y|x,\xi )$ in $\xi$, Assumptions 3.12, 3.13, and 3.14 or Assumptions 3.12, 3.13, and 3.14$'$, the dominated convergence theorem also implies that $\partial \lambda _{T}(\beta )/\partial \beta$ converges uniformly on M to $\partial G(k, \beta , \tau )/\partial \beta$, where

$$\begin{aligned} \partial G(k, \beta , \tau )/\partial \beta= & {} k(k-1)E\Bigg (xx' \Bigg (\tau \int _{x'\beta }^{+\infty }(y-x'\beta )^{k-2} f(y|x,\xi _{0}){\text {d}}y\\&+(1-\tau )\int _{-\infty }^{x'\beta }(x'\beta -y)^{k-2} f(y|x,\xi _{0}){\text {d}}y\Bigg )\Bigg ). \end{aligned}$$

Noting that $\lim _{T\rightarrow \infty }{\tilde{\beta }}_{T}(\tau )={\tilde{\beta }}(\tau )$ and $\partial G(k, \beta , \tau )/\partial \beta$ is nonsingular with respect to $\beta$ in a compact set (see the argument in the proof of Lemma 7.2), there exist positive constants c and $c_{1}$ such that for T large enough

$$\begin{aligned} |\beta -{\tilde{\beta }}_{T}(\tau )|<c\Rightarrow |\lambda _{T}(\beta )| >c_{1}|\beta -{\tilde{\beta }}_{T}(\tau )|. \end{aligned}$$

(7.5)

The (i) item of (N-3) of Huber [26] is satisfied. Now let $\eta (\beta , d)=\sup _{|\alpha -\beta |\le d}|g(\alpha )-g(\beta )|$. Write

$$\begin{aligned} \eta (\beta , d)&=\sup _{|\alpha -\beta |\le d}|(-1)^{1-I(y-x'\alpha<0)}k|\tau -I(y-x'\alpha<0)||y-x'\alpha |^{k-1}x\\&\quad -(-1)^{1-I(y-x'\beta<0)}k|\tau -I(y-x'\beta<0)||y-x'\beta |^{k-1}x|\\&= k|x|\sup _{|\alpha -\beta |\le d}|(-1)^{1-I(y-x'\alpha<0)}|\tau -I(y-x'\alpha<0)||y-x'\alpha |^{k-1}\\&\quad -(-1)^{1-I(y-x'\beta<0)}|\tau -I(y-x'\beta<0)||y-x'\beta |^{k-1}|\\&= k|x|(\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha<0,y-x'\beta<0)(1-\tau )((x'\alpha -y)^{k-1}\\&\quad -(x'\beta -y)^{k-1})|\\&\quad +\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha \ge 0,y-x'\beta \ge 0)\tau ((y-x'\alpha )^{k-1}-(y-x'\beta )^{k-1})|\\&\quad +\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha<0,y-x'\beta \ge 0)((1-\tau )(x'\alpha -y)^{k-1}\\&\quad +\tau (y-x'\beta )^{k-1})|\\&\quad +\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha \ge 0,y-x'\beta <0)(\tau (y-x'\alpha )^{k-1}\\&\quad +(1-\tau )(x'\beta -y)^{k-1})|)\\&=: I_{1}+I_{2}+I_{3}+I_{4}. \end{aligned}$$

We have that, ${\tilde{\alpha }}$ being between $\alpha$ and $\beta$,

$$\begin{aligned} I_{1}\le c_{2}|x|\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha<0,y-x'\beta <0)(x'{\tilde{\alpha }}-y)^{k-2}x'(\alpha -\beta )|. \end{aligned}$$

So,

$$\begin{aligned} E_{T}(I_{1})\le & {} c_{3}E\Bigg (|x|^{2}\int ^{x'{\tilde{\alpha }}}_{-\infty } (x'{\tilde{\alpha }}-y)^{k-2}f(y|x,\xi _{T}){\text {d}}y\Bigg )d\\\le & {} c_{4}E\Bigg (|x|^{2}\int ^{+\infty }_{-\infty }|x'{\tilde{\alpha }} -y|^{k-2}\theta (z){\text {d}}y\Bigg )d=O(d), \end{aligned}$$

where the last equality is due to Assumptions 3.12 and 3.13. Using the same argument as for $I_{1}$, we have $E_{T}(I_{2})=O(d)$. Furthermore,

$$\begin{aligned} I_{3}\le & {} c_{5}|x|\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha <0,y-x'\beta \ge 0)((1-\tau ) (x'\alpha -y)^{k-1}\\&+\tau (y-x'\beta )^{k-1})|\\\le & {} c_{6}|x|\sup _{|\alpha -\beta |\le d}|x'\alpha -x'\beta |\le c_{7}|x|^{2}d. \end{aligned}$$

The second inequality comes from the fact that $a^{r}+b^{r}\le a+b$, for $a,\ b>0$ and $0<r<1$. Thus, Assumption 3.12 implies $E_{T}(I_{3})=O(d)$. Using the same argument as for $I_{4}$, $E_{T}(I_{4})=O(d)$. Additionally,

$$\begin{aligned} \eta ^{2}(\beta , d)= & {} \Big (\sup _{|\alpha -\beta |\le d}|g(\alpha )-g(\beta )|\Big )^{2}\\\le & {} k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(((-1)^{1-I(y-x'\alpha )}|\tau -I(y-x'\alpha<0)||y-x'\alpha |^{k-1})^{2}\\&+\,((-1)^{1-I(y-x'\beta )}|\tau -I(y-x'\beta<0)||y-x'\beta |^{k-1})^{2}\\&-\,2(-1)^{I(y-x'\alpha<0)+I(y-x'\beta<0)} |\tau -I(y-x'\alpha<0)||\tau -I(y-x'\beta<0)||y\\&-x'\alpha |^{k-1}|y-x'\beta |^{k-1})\\\le & {} k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(I(y-x'\alpha<0,y-x'\beta<0)((1-\tau )^{2}(x'\alpha -y)^{2(k-1)}\\&+\,(1-\tau )^{2}(x'\beta -y)^{2(k-1)} -2(1-\tau )^{2}(x'\alpha -y)^{k-1}(x'\beta -y)^{k-1}))\\&+\,k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(I(y-x'\alpha \ge 0,y-x'\beta \ge 0)(\tau ^{2}(y-x'\alpha )^{2(k-1)}\\&+\,\tau ^{2}(y-x'\beta )^{2(k-1)} -2\tau ^{2}(y-x'\alpha )^{k-1}(y-x'\beta )^{k-1}))\\&+\,k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(I(y-x'\alpha<0,y-x'\beta \ge 0)((1-\tau )(x'\alpha -y )^{k-1}\\&+\,\tau (y-x'\beta )^{k-1})^{2})\\&+\,k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(I(y-x'\alpha \ge 0,y\\&-\,x'\beta<0)(\tau (y-x'\alpha )^{k-1}\\&+\,(1-\tau )(x'\beta -y)^{k-1})^{2})\\=: & {} J_{1}+J_{2}+J_{3}+J_{4}. \\ E_{T}(J_{1})= & {} E_{T}\Big (k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}(I(y-x'\alpha<0,y-x'\beta<0)((1-\tau )^{2}((x'\alpha -y)^{k-1}\\&-\,(x'\beta -y)^{k-1})(x'\alpha -y)^{k-1} +(1-\tau )^{2}((x'\beta -y)^{k-1}-(x'\alpha \\&\,-y )^{k-1})(x'\beta -y)^{k-1}))\Big )\\= & {} E_{T}(k^{2}(k-1)|x|^{2}\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha<0,y\\&\,-x'\beta <0)((1-\tau )^{2} (x'{\tilde{\alpha }}_{1}-y)^{k-2}x'(\alpha -\beta )\\&(x'\alpha -y)^{k-1} +(1-\tau )^{2}(x'{\tilde{\alpha }}_{2}-y)^{k-2}x' (\beta -\alpha )(x'\beta -y)^{k-1}))|\\\le & {} c_{8}E\Big (|z|^{k+2}\int _{-\infty }^{+\infty }(|x' {\tilde{\alpha }}_{1}-y|^{k-2}+|x'{\tilde{\alpha }}_{2}-y|^{k-2})\theta (z)dz\Big )d\\= & {} O(d), \end{aligned}$$

where ${\tilde{\alpha }}_{1}$ and ${\tilde{\alpha }}_{2}$ are between $\alpha$ and $\beta$, the second equality is based on the mean value theorem, and the last one is due to Assumptions 3.12 and 3.13. The same argument deduces $E_{T}(J_{2})=O(d)$. For $1<k<1.5$,

$$\begin{aligned} E_{T}(J_{3})= & {} E_{T}\Big (k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha<0,y-x'\beta \ge 0)|((1-\tau )(x'\alpha -y)^{k-1}\\&+\tau (y-x'\beta )^{k-1})^{2}\Big )\\\le & {} c_{9}E_{T}\Big (k^{2}|x|^{2}\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha <0,y-x'\beta \ge 0)|((x'\alpha -y)^{k-1}\\&+(y-x'\beta )^{k-1})^{2}\Big )\\\le & {} c_{10}E(|x|^{2}|x'(\alpha -\beta )|)\le c_{11}d=O(d), \end{aligned}$$

where the first inequality is based on the fact $a^{r}+b^{r}\le c_{12}(a+b)^{1/2}$, for $0<r<0.5$, $a,b>0$ and Assumption 3.12. For $1.5\le k\le 2$,

$$\begin{aligned} E_{T}(J_{3})\le & {} c_{14}E_{T}\Big (|x|^{2}\sup _{|\alpha -\beta |\le d}|I(y-x'\alpha <0,y-x'\beta \ge 0)||x'(\alpha -\beta )|^{2k-2}\Big )\\\le & {} c_{15}E(|x|^{2k})d^{2k-2}\le c_{15}E(|x|^{k+2})d^{2k-2}=O(d), \end{aligned}$$

where the first inequality is due to the concavity of the function $x^{k-1}$, $1<k\le 2$. Using the same argument, we have $E_{T}(J_{4})=O(d)$. Combining the bounds of $I_{i}, J_{i}, i=1,2,3,4$, we obtain

$$\begin{aligned} E_{T}(\eta (\beta , d))=O(d),\ E_{T}(\eta ^{2}(\beta , d))=O(d). \end{aligned}$$

(7.6)

Combining (7.4), (7.5) and (7.6), Assumptions (N-1)-(N-4) of Huber [26] are satisfied uniformly in T. Furthermore, ${\hat{\beta }}(\tau ){\mathop {\rightarrow }\limits ^{\textit{P}}}{\tilde{\beta }}(\tau )$ and $\beta _{T}(\tau )\rightarrow {\tilde{\beta }}(\tau )$ imply ${\hat{\beta }}(\tau )-\beta _{T}(\tau ){\mathop {\rightarrow }\limits ^{\textit{P}}}0$. Theorem 3 in Huber [26] makes sure that

$$\begin{aligned} \sum ^{T}_{t=1}g_{t}(\beta _{T}(\tau ))/T+\sqrt{T} \lambda _{T}({\hat{\beta }}(\tau ))=o_{P}(1), \end{aligned}$$

where $g_{t}(\beta _{T}(\tau ))=-\varphi _{\tau }(y_{t}-x_{t}'\beta _{T}(\tau ))x_{t}$. A mean value expansion of $\lambda _{T}({\hat{\beta }}(\tau ))$ around ${\tilde{\beta }}(\tau )$ provides

$$\begin{aligned} (\partial \lambda _{T}({\dot{\beta }}(\tau ))/\partial \beta ) \sqrt{T}({\hat{\beta }}(\tau )-{\tilde{\beta }}(\tau )) =-\sqrt{T}\lambda _{T}({\tilde{\beta }}(\tau ))-\sum ^{T}_{t=1}g_{t} (\beta _{T}(\tau ))/\sqrt{T}+o_{P}(1), \end{aligned}$$

where ${\dot{\beta }}(\tau )$ between ${\hat{\beta }}(\tau )$ and ${\tilde{\beta }}(\tau )$ is the mean value. Combining continuity of $\partial G(k, \beta , \tau )/\partial \beta$ and uniform convergence of $\partial \lambda _{T}(\beta )/\partial \beta$ ensures $\partial \lambda _{T}({\dot{\beta }}(\tau ))/\partial \beta {\mathop {\rightarrow }\limits ^{\textit{P}}}D$. We can show that results similar to (A.5), (A.6) and (A.7) in Newey [36] hold with $g_{t}(\beta _{T}(\tau ))$ in place of $g_{T}(\theta _{0})$, so using the Lindberg–Feller central limit theorem and the Cramer–Wold device yields that $\sum ^{T}_{t=1}g_{t}(\beta _{T}(\tau ))/\sqrt{T}$ converges to N(0, V) in distribution. Using the argument in the proof of Theorem 3 in Newey and Powell [37], we have $\lim _{T\rightarrow \infty }-\sqrt{T}\lambda _{T}({\tilde{\beta }}(\tau ))=K\zeta$. So using Slutsky’s theorem can complete the proof. $\square$

Proof of Theorem 3.18

By Slutsky’s theorem, it is sufficient to show ${\hat{D}}_{j}{\mathop {\longrightarrow }\limits ^{\textit{P}}}D_{j}$, $j=1, 2, \ldots , n$ and ${\hat{V}}_{ji}{\mathop {\longrightarrow }\limits ^{\textit{P}}}V_{ji}$, $j, i=1, 2, \ldots , n$. Hiding the j subscript, write

$$\begin{aligned}&\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}{\hat{\omega }}_{t}(\tau )|{\hat{u}}_{t}(\tau )|^{k-2} -\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}\omega _{t}(\tau )|u_{t}(\tau )|^{k-2}\\&\quad =\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}{\hat{\beta }}(\tau )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\qquad \cdot (1-\tau )((x'_{t}{\hat{\beta }}(\tau )-y_{t})^{k-2}-(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2})\\&\qquad +\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}{\hat{\beta }}(\tau )>0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )>0)\\&\qquad \cdot \tau ((y_{t}-x'_{t}{\hat{\beta }}(\tau ))^{k-2}-(y_{t}-x'_{t}{\tilde{\beta }}(\tau ))^{k-2})\\&\qquad +\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}{\hat{\beta }}(\tau )\le 0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )\ge 0)\\&\qquad \cdot ((1-\tau )(x'_{t}{\hat{\beta }}(\tau )-y_{t})^{k-2}-\tau (y_{t}-x'_{t}{\tilde{\beta }}(\tau ))^{k-2}) \\&\qquad +\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}{\hat{\beta }}(\tau )\ge 0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )\le 0)\\&\qquad \cdot (\tau (y_{t}-x'_{t}{\hat{\beta }}(\tau ))^{k-2}-(1-\tau )(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2})\\&\quad =: I_{1}+I_{2}+I_{3}+I_{4}. \end{aligned}$$

Letting $\delta =(\text{ sign }(x_{t,1})c_{1}, \text{ sign }(x_{t,2})c_{2}, \ldots , \text{ sign }(x_{t,p})c_{p})^{T}$, where $x_{t,i}$ is the ith component of $x_{t}$ and $c_{i}$ are positive constants, we have, with probability approaching one,

$$\begin{aligned} I_{1,1}(+\delta )&:=\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}({\tilde{\beta }}(\tau )+\delta )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}({\tilde{\beta }}(\tau )+\delta )-y_{t})^{k-2}\\&\le \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}{\hat{\beta }}(\tau )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}{\hat{\beta }}(\tau )-y_{t})^{k-2}=:I_{1,1}\\&\le \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t}({\tilde{\beta }}(\tau )-\delta )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}({\tilde{\beta }}(\tau )-\delta )-y_{t})^{k-2}=:I_{1,1}(-\delta ). \end{aligned}$$

Noting ${\hat{\beta }}(\tau )-{\tilde{\beta }}(\tau )$ converges to 0 in probability, the first inequality $I_{1,1}(+\delta )\le I_{1,1}$ is based on the fact that, with probability approaching one,

$$\begin{aligned} y_{t}-x'_{t}({\tilde{\beta }}(\tau )+\delta )-(y_{t}-x'_{t} {\hat{\beta }}(\tau ))=x'_{t}({\hat{\beta }}(\tau )-{\tilde{\beta }}(\tau )-\delta )<0 \end{aligned}$$

and

$$\begin{aligned} x'_{t}({\tilde{\beta }}(\tau )+\delta )-y_{t}-(x'_{t}{\hat{\beta }} (\tau )-y_{t})=x'_{t}({\tilde{\beta }}(\tau )-{\hat{\beta }}(\tau )+\delta )>0 \end{aligned}$$

and the second inequality $I_{1,1}\le I_{1,1}(-\delta )$ is due to the same argument. Noting $E(x_{t}x'_{t}I(y_{t}-x'_{t}({\tilde{\beta }}(\tau )\pm \delta )<0,y_{t}-x'_{t} {\tilde{\beta }}(\tau )<0)(x'_{t}({\tilde{\beta }}(\tau )\pm \delta )-y_{t})^{k-2})<\infty$, Khintchine law of large numbers yields that

$$\begin{aligned}&I_{1,1}(\pm \delta ){\mathop {\longrightarrow }\limits ^{\textit{P}}} k(k-1)(1-\tau )\\&\qquad \cdot E(x_{t}x'_{t}I(y_{t}-x'_{t}({\tilde{\beta }}(\tau )\pm \delta )<0,y_{t}-x'_{t} {\tilde{\beta }}(\tau )<0)(x'_{t}({\tilde{\beta }}(\tau )\pm \delta )-y_{t})^{k-2}). \end{aligned}$$

Similarly,

$$\begin{aligned} I_{1,2}(+\delta )&:=\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t} -x'_{t}({\tilde{\beta }}(\tau )+\delta )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2}\\&\le \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t} {\hat{\beta }}(\tau )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2}=:I_{1,2}\\&\le \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t} ({\tilde{\beta }}(\tau )-\delta )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )<0)\\&\quad \cdot (1-\tau )(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2}=:I_{1,2}(-\delta ) \end{aligned}$$

and similarly,

$$\begin{aligned} I_{1,2}(\pm \delta )&{\mathop {\longrightarrow }\limits ^{\textit{P}}} k(k-1)(1-\tau )\\&\qquad \cdot E(x_{t}x'_{t}I(y_{t}-x'_{t}({\tilde{\beta }}(\tau )\pm \delta )<0,y_{t}-x'_{t} {\tilde{\beta }}(\tau )<0)(x'_{t}{\tilde{\beta }}(\tau )-y_{t})^{k-2}). \end{aligned}$$

So, letting $c_{i}\rightarrow 0$ in $\delta$, $I_{1}{\mathop {\longrightarrow }\limits ^{\textit{P}}}0$. Using the same argument as the above, $I_{2}{\mathop {\longrightarrow }\limits ^{\textit{P}}}0$.

For any positive constant c, write $J(x,c)\equiv [x'{\tilde{\beta }}-c|x|, x'{\tilde{\beta }}+c|x|]$ and

$$\begin{aligned} E_{T}[I(|u_{j}(\tau )|\le c|x|)|x]=\int _{J(x,c)}f(y|x,\xi _{T}){\text {d}}y \le \int _{J(x,c)}\theta (z){\text {d}}y\equiv \theta _{c}(x). \end{aligned}$$

Noting $\theta (z)$ is integrable in y with probability one, we have $\theta _{c}(x)$ converges to zero monotonically with c by the monotone convergence theorem. According to the continuity of $f(y|x,\xi )$ in Assumption 3.12, $I_{3}$ can be written almost surely as

$$\begin{aligned} I_{3}= & {} \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}I(y_{t}-x'_{t} {\hat{\beta }}(\tau )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )>0)\\&\cdot ((1-\tau )(x'_{t}{\hat{\beta }}(\tau )-y_{t})^{k-2}-\tau (y_{t} -x'_{t}{\tilde{\beta }}(\tau ))^{k-2}). \end{aligned}$$

Furthermore, using the preceding $\delta$, with probability approaching one, we have

$$\begin{aligned} |I_{3}|\le & {} \frac{1}{T}\sum _{t=1}^{T}k(k-1)|x_{t}|^{2}I(y_{t} -x'_{t}{\hat{\beta }}(\tau )<0,y_{t}-x'_{t}{\tilde{\beta }}(\tau )>0)\\&\cdot ((1-\tau )(x'_{t}({\tilde{\beta }}(\tau )+\delta -y_{t}))^{k-2} +\tau (y_{t}-x'_{t}{\tilde{\beta }}(\tau ))^{k-2}).\\\le & {} \frac{1}{T}\sum _{t=1}^{T}k(k-1)|x_{t}|^{2} ((1-\tau )|x'_{t}({\tilde{\beta }}(\tau )+\delta )-y_{t}|^{k-2} +\tau |y_{t}-x'_{t}{\tilde{\beta }}(\tau )|^{k-2})\\&\cdot I(|u_{t}(\tau )|\le |\delta ||x_{t}|)\\\le & {} E(k(k-1)|x_{t}|^{2}\theta _{|\delta |}(x_{t}) ((1-\tau )|x'_{t}({\tilde{\beta }}(\tau )+\delta )-y_{t}|^{k-2} +\tau |y_{t}-x'_{t}{\tilde{\beta }}(\tau )|^{k-2}))\\&+|\delta |\\\le & {} cE(|x_{t}|^{2}\theta _{|\delta |}(x_{t}))+|\delta |, \end{aligned}$$

where the third inequality follows from Khintchine law of large numbers and the last inequality is based on Assumption 3.13. Since $E(|x_{t}|^{2}\theta _{|\delta |}(x_{t}))+|\delta |$ converges to zero with $|\delta |$ by the monotone convergence theorem, we have $I_{3}{\mathop {\longrightarrow }\limits ^{\textit{P}}}0$. Using the same argument, we also have $I_{4}{\mathop {\longrightarrow }\limits ^{\textit{P}}}0$. The triangle inequality yields

$$\begin{aligned} |{\hat{D}}-D|\le & {} \left| \frac{1}{T}\sum _{t=1}^{T}k(k-1) x_{t}x'_{t}{\hat{\omega }}_{t}(\tau )|{\hat{u}}_{t}(\tau )|^{k-2}\right. \nonumber \\&\left. -\frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}\omega _{t}(\tau )|u_{t}(\tau )|^{k-2}\right| \nonumber \\&+\left| \frac{1}{T}\sum _{t=1}^{T}k(k-1)x_{t}x'_{t}\omega _{t}(\tau )|u_{t}(\tau )|^{k-2}|-D\right| . \end{aligned}$$

(7.7)

The first term in the right-hand side of inequality (7.7) converges to zero in probability by combining $I_{i}{\mathop {\longrightarrow }\limits ^{\textit{P}}}0$, $i=1,2,3,4$, and the second term converges to zero according to Khintchine law of large numbers. So we have ${\hat{D}}_{j}{\mathop {\longrightarrow }\limits ^{\textit{P}}}D_{j}$. Focusing on ${\hat{V}}_{ji}$, it is easy to show there are positive constants $c_{16}$, $c_{17}$ and $c_{18}$ such that

$$\begin{aligned} |\varphi _{\tau }(y_{t}-x'_{t}\beta _{1})\varphi _{\theta }(y_{t} -x'_{t}\beta _{2})x_{t}x'_{t})|\le |z_{t}|^{2k}(c_{16}+c_{17}|\beta _{1}|^{k-1}+c_{18}|\beta _{2}|^{k-1}). \end{aligned}$$

Using the method in the proof of Theorem 2.2 in Newey [36] can prove ${\hat{V}}_{ji}{\mathop {\longrightarrow }\limits ^{\textit{P}}}V_{ji}$. $\square$

Proof of Theorem 3.23

The proof of (i) is the same as Theorem 3.17, for Assumption 3.20 easily induces Assumption 3.10. To prove (ii), it is sufficient to prove the case $n=1$. It is sufficient to prove that ${\tilde{D}}\rightarrow {\bar{D}}$, ${\tilde{V}}\rightarrow {\bar{V}}$, and ${\tilde{D}}^{-1}{\tilde{K}}\gamma _{0}\rightarrow {\bar{K}}$, as $k\rightarrow 1$. We mainly focus on

$$\begin{aligned} (\partial \lambda _{T}({\dot{\beta }}(\tau ))/\partial \beta )\sqrt{T} ({\hat{\beta }}(\tau )-{\tilde{\beta }}(\tau )) =-\sqrt{T}\lambda _{T}({\tilde{\beta }}(\tau ))-\sum ^{T}_{t=1}g_{t} (\beta _{T}(\tau ))/\sqrt{T}+o_{P}(1),\nonumber \\ \end{aligned}$$

(7.8)

where ${\dot{\beta }}(\tau )$ between ${\hat{\beta }}(\tau )$ and ${\tilde{\beta }}(\tau )$ is the mean value. Write, $f_{y}$ being the density of y,

$$\begin{aligned} {\tilde{D}}= & {} E(k(k-1)\omega (\tau )|u(\tau )|^{k-2}xx')\\= & {} k(k-1)E\Bigg (xx'\int _{R}|\tau -I(y-x'{\tilde{\beta }} (\tau ))||y-x'{\tilde{\beta }}(\tau )|^{k-2}f_{y}(y){\text {d}}y\Bigg )\\= & {} kE\Bigg (xx'\Bigg (\int _{0}^{\infty }(1-\tau )f_{y}(x'{\tilde{\beta }} (\tau )-z)dz^{k-1}+\int _{0}^{\infty }\tau f_{y}(x'{\tilde{\beta }}(\tau )+z)dz^{k-1}\Bigg )\Bigg )\\= & {} kE\Bigg (xx'\Bigg (\int _{0}^{\infty }(1-\tau )f_{\varepsilon } \Bigg (\frac{x'({\tilde{\beta }}(\tau )-\beta )-z}{1+x'\frac{\gamma _{0}}{\sqrt{T}}}\Bigg )\frac{1}{1+x\frac{\gamma _{0}}{\sqrt{T}}}dz^{k-1}\\&+\int _{0}^{\infty }\tau f_{\varepsilon }\Bigg (\frac{x'({\tilde{\beta }}(\tau )-\beta )+z}{1+x'\frac{\gamma _{0}}{\sqrt{T}}}\Big )\frac{1}{1+x'\frac{\gamma _{0}}{\sqrt{T}}}dz^{k-1}\Bigg )\Bigg )\\\sim & {} k E\Bigg (xx'\Bigg (\int _{0}^{\infty }(1-\tau )f_{\varepsilon } (x'({\tilde{\beta }}(\tau )-\beta )-z)dz^{k-1}\\&+\int _{0}^{\infty }\tau f_{\varepsilon }(x'({\tilde{\beta }}(\tau )-\beta )+z)dz^{k-1}\Bigg )\Bigg )\\= & {} k E\Bigg (xx'\Bigg (\int _{0}^{\infty }(1-\tau )f_{\varepsilon } (q_{\varepsilon }(\tau )-z)dz^{k-1} +\int _{0}^{\infty }\tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z)dz^{k-1}\Bigg )\Bigg ), \end{aligned}$$

where the ‘$\sim$’ above is obtained by the dominated convergence theorem as $T\rightarrow \infty$. Note that, as $k\rightarrow 1$,

$$\begin{aligned}&\int _{0}^{\infty }((1-\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )-z)+ \tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z))dz^{k-1}\\&\quad =((1-\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )-z)+ \tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z))z^{k-1}|^{\infty }_{0}\\&\qquad -\int ^{\infty }_{0}z^{k-1} d((1-\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )-z)+ \tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z))\\&\quad =-\int ^{\infty }_{0}z^{k-1} d((1-\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )-z)+ \tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z))\\&\quad \rightarrow -\int ^{\infty }_{0} d((1-\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )-z)+ \tau f_{\varepsilon }(q_{\varepsilon }(\tau )+z))\\&\quad =f_{\varepsilon }(q_{\varepsilon }(\tau )), \end{aligned}$$

where the second equality is due to Assumption 3.21, and the ‘$\rightarrow$’ is due to Assumption 3.22 and the dominated convergence theorem. So we have that ${\tilde{D}}\rightarrow {\bar{D}}$ as $k\rightarrow 1$ hence $\partial \lambda _{T}({\dot{\beta }}(\tau ))/\partial \beta \rightarrow {\bar{D}}$. As $k\rightarrow 1$,

$$\begin{aligned} {\tilde{V}}_{jk}&\rightarrow E(\varphi _{\tau _{j}}(u(\tau _{j})) \varphi _{\tau _{k}}(u(\tau _{k})) xx')\\&= E(xx'E((-1)^{I(y-x'{\tilde{\beta }}(\tau _{j})<0)}|\tau _{j}-I(y -x'{\tilde{\beta }}(\tau _{j})<0)|\\&\quad (-1)^{I(y-x'{\tilde{\beta }}(\tau _{k})<0)}|\tau _{k}-I(y -x'{\tilde{\beta }}(\tau _{k})<0)||x))\\&= E(xx'E((-1)^{I(\varepsilon<q_{\varepsilon }(\tau _{j}))}|\tau _{j} -I(\varepsilon<q_{\varepsilon }(\tau _{j}))|\\&\quad (-1)^{I(\varepsilon<q_{\varepsilon }(\tau _{k}))}|\tau _{k} -I(\varepsilon <q_{\varepsilon }(\tau _{k}))|))\\&\quad =(\text{ min }(\tau _{j},\tau _{k})-\tau _{j}\tau _{k})E(xx')={\bar{V}}_{jk}. \end{aligned}$$

Assumption 3.12 and the dominated convergence theorem yield that

$$\begin{aligned} \lim _{k\rightarrow 1}-\sqrt{T}\lambda _{T}({\tilde{\beta }}(\tau ))=\sqrt{T}E_{T} ((-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)|x).\qquad \end{aligned}$$

(7.9)

Letting $\gamma :=\frac{\gamma _{0}}{\sqrt{T}}$, a mean value expansion of the right-hand side of (7.9) around zero shows,${\tilde{\gamma }}$ being the mean value,

$$\begin{aligned}&\sqrt{T}E ((-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)|x)\nonumber \\&\quad =\sqrt{T}\frac{\partial (\int _{X\times Y}(-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0) |f_{\varepsilon }(\frac{y-x'\beta }{1+x'\gamma })\frac{g(x)}{1+x'\gamma }{\text {d}}y{\text {d}}\mu _{x})}{\partial \gamma }\Bigg |_{\gamma ={\tilde{\gamma }}}\Big (\frac{\gamma _{0}}{\sqrt{T}}\Big )\nonumber \\&\quad =\frac{\partial (\int _{X\times Y}(-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0) |f_{\varepsilon }(\frac{y-x'\beta }{1+x'\gamma })\frac{g(x)}{1+x'\gamma }{\text {d}}y{\text {d}}\mu _{x})}{\partial \gamma }\Bigg |_{\gamma ={\tilde{\gamma }}}\gamma _{0}.\nonumber \\ \end{aligned}$$

(7.10)

Furthermore,

$$\begin{aligned}&\frac{\partial (\int _{X\times Y}(-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0) |f_{\varepsilon }(\frac{y-x'\beta }{1+x'\gamma })\frac{g(x)}{1+x'\gamma }{\text {d}}y{\text {d}}\mu _{x})}{\partial \gamma }\Bigg |_{\gamma ={\tilde{\gamma }}}\nonumber \\&\quad =\int _{X\times Y} (-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)|\nonumber \\&\qquad \Big (-f^{(1)}_{\varepsilon }\Big (\frac{y-x'\beta }{1+x'{\tilde{\gamma }}}\Big )\frac{y-x'\beta }{(1+x'{\tilde{\gamma }})^{3}}xx' -f_{\varepsilon }\Big (\frac{y-x'\beta }{1+x'{\tilde{\gamma }}}\Big )\frac{1}{(1+x'{\tilde{\gamma }})^{2}}xx'\Big )g(x){\text {d}}y{\text {d}}\mu _{x}\nonumber \\&\quad =E\Bigg (xx'\int ^{\infty }_{-\infty }(-1)^{I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)|\nonumber \\&\qquad \Bigg (-f^{(1)}_{\varepsilon }\Big (\frac{y-x'\beta }{1+x'{\tilde{\gamma }}}\Big )\frac{y-x'\beta }{(1+x'{\tilde{\gamma }})^{3}} -f_{\varepsilon }\Big (\frac{y-x'\beta }{1+x'{\tilde{\gamma }}}\Big )\frac{1}{(1+x'{\tilde{\gamma }})^{2}}\Bigg ){\text {d}}y\Bigg )\nonumber \\&\quad =:E(xx'(I_{1}+I_{2})). \end{aligned}$$

(7.11)

We have that

$$\begin{aligned} \lim _{T\rightarrow \infty }I_{1}= & {} \int ^{\infty }_{-\infty }(-1)^{1+I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)| f^{(1)}_{\varepsilon }(y-x'\beta )(y-x'\beta ){\text {d}}y\nonumber \\= & {} \int ^{x'{\tilde{\beta }}(\tau )}_{-\infty }(1-\tau )f^{(1)}_{\varepsilon }(y-x'\beta )(y-x'\beta ){\text {d}}y\nonumber \\&-\int _{x'{\tilde{\beta }}(\tau )}^{\infty }\tau f^{(1)}_{\varepsilon }(y-x'\beta )(y-x'\beta ){\text {d}}y\nonumber \\= & {} \int ^{q_{\varepsilon }(\tau )}_{-\infty }(1-\tau )f^{(1)}_{\varepsilon }(y)y {\text {d}}y-\int ^{\infty }_{q_{\varepsilon }(\tau )}\tau f^{(1)}_{\varepsilon }(y)y {\text {d}}y\nonumber \\= & {} \int ^{q_{\varepsilon }(\tau )}_{-\infty }(1-\tau )y df_{\varepsilon }(y)-\int ^{\infty }_{q_{\varepsilon }(\tau )}\tau y df_{\varepsilon }(y)\nonumber \\= & {} (1-\tau )y f_{\varepsilon }(y)|^{q_{\varepsilon }(\tau )}_{-\infty } -(1-\tau )\int ^{q_{\varepsilon }(\tau )}_{-\infty }f_{\varepsilon }(y){\text {d}}y -\tau y f_{\varepsilon }(y)|^{\infty }_{q_{\varepsilon }(\tau )}\nonumber \\&+\int ^{\infty }_{q_{\varepsilon }(\tau )}\tau f_{\varepsilon }(y){\text {d}}y\nonumber \\= & {} q_{\varepsilon }(\tau )f_{\varepsilon }(q_{\varepsilon }(\tau )) -\int ^{q_{\varepsilon }(\tau )}_{-\infty }f_{\varepsilon }(y){\text {d}}y+\tau \end{aligned}$$

(7.12)

and

$$\begin{aligned} \lim _{T\rightarrow \infty }I_{2}= & {} \int ^{\infty }_{-\infty }(-1)^{1 +I(y-x'{\tilde{\beta }}(\tau )<0)}|\tau -I(y-x'{\tilde{\beta }}(\tau )<0)| f_{\varepsilon }(y-x'\beta ){\text {d}}y\nonumber \\= & {} \int ^{q_{\varepsilon }(\tau )}_{-\infty }(1-\tau )f_{\varepsilon }(y){\text {d}}y -\int ^{\infty }_{q_{\varepsilon }(\tau )}\tau f_{\varepsilon }(y){\text {d}}y=\int ^{q_{\varepsilon }(\tau )}_{-\infty }f_{\varepsilon }(y){\text {d}}y-\tau .\nonumber \\ \end{aligned}$$

(7.13)

According to the dominated convergence theorem, (7.9)–(7.13) deduce

$$\begin{aligned} \lim _{T\rightarrow \infty }\lim _{k\rightarrow 1} -\sqrt{T}\lambda _{T}({\tilde{\beta }}(\tau )) =\gamma _{0}q_{\varepsilon }(\tau )f_{\varepsilon } (q_{\varepsilon }(\tau ))E(xx'). \end{aligned}$$

According to (7.8) and $\partial \lambda _{T}({\dot{\beta }}(\tau ))/\partial \beta \rightarrow {\bar{D}}$, as $k\rightarrow 1$, we have that the expectation of $\sqrt{T}({\hat{\beta }}(\tau )-{\tilde{\beta }}(\tau ))$ converges to $\gamma _{0}q_{\varepsilon }(\tau )$, i.e., ${\tilde{D}}^{-1}{\tilde{K}}\gamma _{0}\rightarrow {\bar{K}}$. $\square$

Proof of Theorem 4.3

First we need to prove the asymptotic normality of ${\hat{\eta }}$, and the consistency of the related covariance matrix estimator like in Theorem 3.18. Then the noncentral Chi-square asymptotic distribution of TS follows naturally. It is sufficient to verify that conditions in Theorems 3.17 and 3.18 are satisfied. Denote $I\equiv (-1/2, 1/2)$, and write, for $\varsigma$ in I,

$$\begin{aligned} \frac{1}{1+\varsigma }f_{\varepsilon }\Big (\frac{u}{1+\varsigma }\Big )\le & {} 2f_{\varepsilon }\Big (\frac{u}{1+\varsigma }\Big )\\\le & {} 2C/(1+|\frac{2u}{3}|^{k+3+c}) . \end{aligned}$$

There exists a 2p-dimension open neighborhood of zero, $U_{0}$, such that, for $\xi$ in $U_{0}$, $x'_{t}\xi _{Th}+I(\varepsilon _{t}>0)x'_{t}\xi _{Ts}$ is an element of I with probability one. Noting that

$$\begin{aligned} f(y|x,\xi )=\frac{1}{1+x'_{t}\xi _{Th}+I(\varepsilon _{t}>0)x'_{t}\xi _{Ts}} f_{\varepsilon }\Bigg (\frac{y-x'\beta _{0}}{1+x'_{t}\xi _{Th} +I(\varepsilon _{t}>0)x'_{t}\xi _{Ts}}\Bigg ), \end{aligned}$$

the continuity of $f(y|x,\xi )$ in y and $\xi$ holds based the continuity of $f_{\varepsilon }$. When taking $\theta (z)=2C/(1+(2|y-x'\beta _{0}|/3)^{k+3+c})$, we can show that domination conditions of Assumption 3.12 hold. Assumption 3.14$'$ is satisfied if $\varepsilon _{t}$ is not equal to $\infty$ almost surely; Assumption 3.13 is satisfied using the simple calculation. In the following, we prove the continuous differentiability of $E(x\varphi _{\tau }(y-x'\beta (\tau ))|\xi )$ and calculate noncentrality parameter of the noncentral Chi-squared distribution. The parameter in general can be written as:

$$\begin{aligned} (HD^{-1}K\zeta )'(HD^{-1}VD^{-1}H')^{-1}HD^{-1}K\zeta . \end{aligned}$$

(7.14)

Note that, for $\xi :=(\xi '_{Th}, \xi '_{Ts})'=0$, $u(\tau )=y_{t}-x'_{t}{\tilde{\beta }}(\tau )=u_{t}-\mu (\tau )$ is dependent of $x_{t}$. We have $D_{j}=l(\tau _{j})L$, and hence, $D=\text{ diag }(l(\tau _{1}), \ldots , l(\tau _{n}))\otimes L$, and $V=(c(\tau _{j}, \tau _{k}))_{n\times n}\otimes L$. Using the matrix inversion law of Kronecker products, we have $D^{-1}VD^{-1}=\Omega \otimes L^{-1}$. Furthermore, $E(-\varphi (u(\tau ))x_{t}|\xi )=E(x_{t}E(-\varphi (u(\tau ))|x_{t}, \xi ))$ and, for $\mu (\tau )>0$,

$$\begin{aligned} E(-\varphi (u(\tau ))|x_{t}, \xi )= & {} E((-1)^{1+I(u_{t}<\mu (\tau ))}k|\tau -I(u_{t} <\mu (\tau ))||u_{t}-\mu (\tau )|^{k-1}|x_{t}, \xi )\\= & {} (1-\tau )\int ^{0}_{-\infty }k\frac{(\mu (\tau )-r)^{k -1}}{\varsigma _{th}}f_{\varepsilon }\Big (\frac{r}{\varsigma _{th}}\Big ){\text {d}}r\\&+(1-\tau )\int ^{\mu (\tau )}_{0}k\frac{(\mu (\tau )-r)^{k-1}}{\varsigma _{tp}}f_{\varepsilon }\Big (\frac{r}{\varsigma _{tp}}\Big ){\text {d}}r\\&-\tau \int ^{\infty }_{\mu (\tau )}k\frac{(r-\mu (\tau ))^{k -1}}{\varsigma _{tp}}f_{\varepsilon }\Big (\frac{r}{\varsigma _{tp}}\Big ){\text {d}}r\\= & {} (1-\tau )\int ^{0}_{-\infty }k(\mu (\tau )-\varsigma _{th}r)^{k-1}f_{\varepsilon }(r){\text {d}}r\\&+(1-\tau )\int ^{\mu (\tau )/\varsigma _{tp}}_{0}k(\mu (\tau ) -\varsigma _{tp}r)^{k-1}f_{\varepsilon }(r){\text {d}}r\\&-\tau \int ^{\infty }_{\mu (\tau )/\varsigma _{tp}}k(\varsigma _{tp}r -\mu (\tau ))^{k-1}f_{\varepsilon }(r){\text {d}}r, \end{aligned}$$

where $\varsigma _{th}=1+x'_{t}\xi _{Th}$, and $\varsigma _{tp}=1+x'_{t}\xi _{Th}+x'_{t}\xi _{Ts}$. We have

$$\begin{aligned} \partial (E(-\varphi (u(\tau ))|x_{t}, 0))/\partial \xi =(\upsilon 1(\tau ), \upsilon 2(\tau ))'\otimes x_{t}, \end{aligned}$$

which can be dominated by an integrable function, thus

$$\begin{aligned} \partial (E(-\varphi (u(\tau ))x_{t}|0))/\partial \xi =(\upsilon 1(\tau ), \upsilon 2(\tau ))'\otimes L. \end{aligned}$$

(7.15)

For $\mu (\tau )<0$, we still have the result of (7.15) by the similar argument. So the continuous differentiability in Assumption 3.11 has been examined. We have $D^{-1}_{j}K_{j}=(\upsilon 1(\tau _{j})/l(\tau _{j}), \upsilon 2(\tau _{j})/l(\tau _{j}))\otimes I_{p}$, and obtain (4.6) in Theorem 4.3 according to (7.14). $\square$

Proof of Lemma 7.1

By Condition 3.1, we have that $Q_{\tau ,k}(y_{t}-x'_{t}b)f_{t}(y_{t}|x_{t})g_{t}(x_{t})$ is continuous in $b\in {\mathcal {B}}_{1}$ uniformly in t almost surely. The definition of $Q_{\tau ,k}(y_{t}-x'_{t}b)$ makes sure that it is measurable for each t and each $b\in {\mathcal {B}}_{1}$. Condition 3.2 yields that

$$\begin{aligned}&\int \sup _{t\ge 1,b\in {\mathcal {B}}_{1}}|Q_{\tau ,k}(y_{t} -x'_{t}b)|f_{t}(y_{t}|x_{t})g_{t}(x_{t}){\text {d}}M_{z,t}\\&\quad =\int \sup _{t\ge 1,b\in {\mathcal {B}}_{1}}|\tau -I(y_{t}-x'_{t}b )||y_{t}-x'_{t}b|^{k}f_{t}(y_{t}|x_{t})g_{t}(x_{t}){\text {d}}M_{z,t}\\&\quad \le c\int \sup _{t\ge 1,b\in {\mathcal {B}}_{1}}(1+\Vert b\Vert )|z_{t}|^{k} f_{t}(y_{t}|x_{t})g_{t}(x_{t}){\text {d}}M_{z,t}<\infty . \end{aligned}$$

Define $Q^{*}_{\tau ,k}(z_{t}, b, r):=\sup \{Q_{\tau ,k}(y_{t}-x'_{t}{\tilde{b}}), {\tilde{b}}\in \delta (b,r)\}$ and $Q_{*\tau ,k}(z_{t}, b, r):=\inf \{Q_{\tau ,k}(y_{t}-x'_{t}{\tilde{b}}), {\tilde{b}}\in \delta (b,r)\}$, with $\delta (b,r)=\{{\tilde{b}}\in {\mathcal {B}}_{1}, \Vert {\tilde{b}}-b\Vert <\delta \}$. We have $\{Q^{*}_{\tau ,k}(z_{t}, b, r)\le y\}=\{\max \{Q_{\tau ,k}(y_{t}-x'_{t}{\tilde{b}}), {\tilde{b}}\in \delta (b,r)\cap Q^{p}\}\le y\}$, $Q^{p}$ being the space of p-dimension rational numbers, as $Q_{\tau ,k}(y_{t}-x'_{t}{\tilde{b}})$ is the continuous function of b for any $z_{t}$. Thus, $Q^{*}_{\tau ,k}(z_{t}, b, r)$ is a random variable and so do $Q_{*\tau ,k}(z_{t}, b, r)$ using the same argument. These show that Assumptions A1, A2 and A6 in Andrews [1] are satisfied and then, using his Corollary 3 can complete our proof. $\square$

Proof of Lemma 7.2

Write $M(b,\tau ,T):=\frac{1}{T}\sum _{t=1}^{T}E(Q_{\tau ,k}(y_{t}-x'_{t}b))$ and $g_{t}(b):=\partial E(Q_{\tau ,k}(y_{t}-x'_{t}b))\partial b$. Obviously, there are positive constants c and d such that $g_{t}(b)\le (c+d|b|)|z_{t}|$. Hence, $g_{t}(b)$ is controlled by an integrable function on a neighborhood of any b according to Condition 3.2. So we can calculate the derivative of $g_{t}(b)$ as follows.

$$\begin{aligned} \partial M(b,\tau ,T)/\partial b&=\frac{k}{T}\sum _{t=1}^{T}E \bigg (x_{t}\bigg (-\tau \int ^{\infty }_{x_{t}'b}(y-x_{t}'b)^{k-1}f_{t}(y|x_{t}){\text {d}}y\\&\quad +(1-\tau )\int ^{x_{t}'b}_{-\infty }(x_{t}'b-y)^{k-1}f_{t}(y|x_{t}){\text {d}}y\bigg )\bigg )\\&=: G_{T}(b). \end{aligned}$$

Functions $\int ^{\infty }_{x_{t}'b}(y-x_{t}'b)^{k-1}f_{t}(y|x_{t}){\text {d}}y$ and $\int ^{x_{t}'b}_{-\infty }(x_{t}'b-y)^{k-1}f_{t}(y|x_{t}){\text {d}}y$ are continuously differentiable in b, and their derivatives are controlled uniformly in $x_{t}$ and in b2B by integrable functions using Condition A3. Thus, the derivative of $G_{T}(b)$ is

$$\begin{aligned} \nonumber \partial G_{T}(b)/\partial b= & {} \frac{k(k-1)}{T} \sum _{t=1}^{T}E\bigg (x_{t}x_{t}'\bigg (\tau \int ^{\infty }_{x_{t}'b} (y-x_{t}'b)^{k-2}f_{t}(y|x_{t}){\text {d}}y\\&+(1-\tau )\int ^{x_{t}'b}_{-\infty }(x_{t}'b-y)^{k-2}f_{t}(y|x_{t}){\text {d}}y\bigg )\bigg ). \end{aligned}$$

(7.16)

The equation makes sure that there is a positive constant c such that

$$\begin{aligned} \partial G_{T}(b)/\partial b-c k(k-1)\frac{1}{T}\sum _{t=1}^{T}E\bigg (x_{t}x_{t}' \bigg (\int ^{+\infty }_{-\infty }|y-x'_{t}b|^{k-2}f_{t}(y|x_{t}){\text {d}}y\bigg )\bigg ) \end{aligned}$$

or combining with Condition 3.5$'$,

$$\begin{aligned} \partial G_{T}(b)/\partial b-c k(k-1)\frac{1}{T}\sum _{t=1}^{T}E(x_{t}x'_{t}) \end{aligned}$$

is positive semi-definite for $b\in {\mathcal {B}}_{3}$ (a compact subset of $R^{p}$) and thus, $\partial G_{T}(b)/\partial b$ is positive definite for $b\in {\mathcal {B}}_{3}$ using Condition 3.5 or Condition 3.5$'$. So, for $b, {\tilde{b}}\in {\mathcal {B}}_{3}$,

$$\begin{aligned} \nonumber M(b,\tau , T)-M({\tilde{b}}, \tau , T)= & {} G_{T}({\tilde{b}})'(b-{\tilde{b}})+(b-{\tilde{b}})'(\partial G_{T}({\dot{b}})/\partial b)(b-{\tilde{b}})\\\ge & {} G_{T}({\tilde{b}})'(b-{\tilde{b}})+m_{e}p|b-{\tilde{b}}|^{2}, \end{aligned}$$

(7.17)

where ${\dot{b}}$ is the mean value and $m_{e}$ the minimum eigenvalue of $\partial G_{T}({\dot{b}})/\partial b$. The function $M(b,\tau ,T)$ is convex as $E(Q_{\tau ,k}(y_{t}-x'_{t}b))$ is convex with respect to b and converges to infinity as $|b|\rightarrow \infty$. So there is a global minimum ${\tilde{\beta }}(k, \tau )$ and $G_{T}({\tilde{\beta }}(k, \tau ))=0$. Letting ${\tilde{b}}={\tilde{\beta }}(k, \tau )$ and using reduction to absurdity (7.17) show that the global minimum is also unique one over $R^{p}$. $\square$