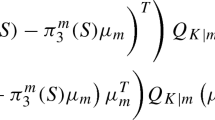Abstract
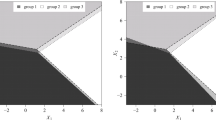
In this paper, a linear discriminant analysis (LDA) is performed in the Gini sense (GDA). Maximizing the generalized Gini gross between-group matrix allows the data to be projected onto discriminant axes. Different methods are investigated, the geometrical approach—based on a particular distance—and the probabilistic approach, which consists in employing the generalized Gini within-group matrix in order to compute the conditional probability of ranking observations in specific groups. Tests based on U-statistics are proposed in order to test for discriminant variables instead of using the well-known Student test that requires homoskedasticity. Monte Carlo simulations show the robustness and the superiority of the GDA on contaminated data compared with various linear classifiers such as logit, SVM and LDA.



Similar content being viewed by others
Notes
In the Gini literature, the expression between-group inequality (or between-group variability) is only used if the variables of the different groups do not overlap, see [18] for an overview of this literature. In the overlapping case, the gross between-group Gini term can be further decomposed into a stratification term ( [15, 17]) or an overlapping term (i.e. Gini’s transvariation, see [6]) plus a between-group inequality term (or between-group variability term) that accounts for the inequality (or variability) between the variables means.
Strictly speaking the coGini of two random variables X, Y is either given by \(\text {Cov}(X,G(Y))\) or \(\text {Cov}(Y,F(X))\), see Yitzhaki and Schechtman [18], page 40.
Proposition 2.1 outlines the fact that the generalized Gini gross between-group correlation matrix is obtained from \(GC_{\nu ,w}({\textit{\textbf{X}}})\) as a residual. The Gini decomposition mimics the variance one: the within-group term measures the gap between each observation in group \({\mathscr {S}}_g\) and the mean of group \({\mathscr {S}}_g\), while the gross between-group term measures the gap between the mean of each group \({\mathscr {S}}_g\) and the grand mean. Of course, because of the reranking term \(\textit{\textbf{R}}_{\mathbf {z},\nu }^c\), we cannot see the overlap or stratification Gini term and the true between-group Gini term, see e.g. [6, 17]. Future researches could be done to show that the classification could be performed on the overlap term only as in [11].
Following Eq. (6) it is also possible to use \([GC_{\nu ,w}({\textit{\textbf{X}}}) + GC_{\nu ,w}({\textit{\textbf{X}}})^{\intercal }]^{-1}\) instead of \(GC_{\nu ,w}({\textit{\textbf{X}}})^{-1}\).
A confusion matrix allows one to compute the performance of a classifier. It consists in measuring the rate of good (bad) classification and also the rate of false negative and false positive.
Hinge loss is a usual loss function used in machine learning for training classifiers.
References
Baccini, A., Besse, P., de Falguerolles, A.: A \(L_1\) norm PCA and a heuristic approach. In: Didday, E., Lechevalier, Y., Opitz, O. (eds.) Ordinal and Symbolic Data Analysis, pp. 359–368. Springer, New York (1996)
Calò, D.G.: On a transvariation based measure of group separability. J. Classif. 23(1), 143–167 (2006)
Carcea, M., Serfling, R.: A Gini autocovariance function for time series modeling. J. Time Ser. Anal. 36, 817–38 (2015)
Charpentier, A., Ka, N., Mussard, S., Ndiaye, O.: Gini regressions and heteroskedasticity. Econometrics 7(1), 4 (2019a)
Charpentier, A., Mussard, S. & Ouraga, T.: Principal component analysis: a generalized Gini approach. Working paper # 2019-02 CHROME, University of nîmes, hal-02340386v1. (2019b)
Dagum, C.: A new approach to the decomposition of the Gini income inequality ratio. Empir. Econ. 22, 515–531 (1997)
Furman, E., Zitikis, R.: Beyond the Pearson correlation: heavy-tailed risks. Weighted Gini correlations, and a Gini-type weighted insurance pricing model. ASTIM Bull. J. Int. Actuar. Assoc. 47(03), 919–942 (2017)
Ka, N., Mussard, S.: \(\ell _1\) Regressions: Gini estimators for fixed effects panel data. J. Appl. Stat. 43(8), 1436–1446 (2016)
Li, C., Shaoa, Y.-H., Deng, N.-Y.: Robust L1-norm two-dimensional linear discriminant analysis. Neural Netw. 65, 92–104 (2015)
Olkin, I., Yitzhaki, S.: Gini regression analysis. Int. Stat. Rev. 60(2), 185–196 (1992)
Montanari, A.: Linear discriminant analysis and transvariation. J. Classif. 21(1), 71–88 (2004)
Schechtman, E., Yitzhaki, S.: A measure of association based on Gini’s mean difference. Commun. Stat. Theory Methods 16, 207–231 (1987)
Yaari, M.E.: The dual theory of choice under risk. Econometrica 55, 99–115 (1987)
Yaari, M.E.: A controversial proposal concerning inequality measurement. J. Econ. Theory 44, 381–397 (1988)
Yitzhaki, S.: Economic distance and overlapping of distributions. J. Econom. 61, 147–159 (1994)
Yitzhaki, S.: Gini’s mean difference: a superior measure of variability for non-normal distributions. Metron I(2), 285–316 (2003)
Yitzhaki, S., Lerman, R.: Income stratification and income inequality. Rev. Income Wealth 37, 313–329 (1991)
Yitzhaki, S., Schechtman, E.: The Gini Methodology: A Primer on a Statistical Methodology. Springer, New York (2013)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors acknowledge the editors of the special issue for the 100th anniversary of METRON, Giovanni Maria Giorgi, Jacques Silber and Roberto Zelli. The reviewers are also acknowledged for their interesting comments and suggestions. The usual disclaimer applies.
Appendix: Proofs
Appendix: Proofs
Proof of Proposition 2.1
The Gini variability decomposition is:
Since,
then,
Let \(\bar{{\textit{\textbf{Z}}}_\nu }^g\) is the \(n\times K\) matrix in which each line i corresponds to the mean \({\bar{\mathbf {z}}}^g\) of the ith observation of \({\textit{\textbf{Z}}}_\nu \) being in \({\mathscr {S}}_g\), then by Eq. (9):
By Eq. (9) again:
and this ends the proof. \(\square \)
Proof of Proposition 2.2
-
(i)
Since \(GC_{\nu ,w}({\textit{\textbf{X}}})\) and \(GC_{\nu ,b}({\textit{\textbf{X}}})\) are not symmetric matrices, it comes that maximizing
$$\begin{aligned} \lambda :=\frac{\mathbf {u}^{\intercal } GC_{\nu ,b}({\textit{\textbf{X}}}) \mathbf {u}}{\mathbf {u}^{\intercal } GC_\nu ({\textit{\textbf{X}}}) \mathbf {u}} \end{aligned}$$yields,
$$\begin{aligned} \frac{ [GC_{\nu ,b}({\textit{\textbf{X}}})+GC_{\nu ,b}({\textit{\textbf{X}}})^{\intercal }] \mathbf {u} \left[ \mathbf {u}^{\intercal } GC_\nu ({\textit{\textbf{X}}}) \mathbf {u} \right] - \left[ \mathbf {u}^{\intercal } GC_{\nu ,b}({\textit{\textbf{X}}}) \mathbf {u} \right] [GC_\nu ({\textit{\textbf{X}}})+GC_\nu ({\textit{\textbf{X}}})^{\intercal }] \mathbf {u}}{[\mathbf {u}^{\intercal } GC_\nu ({\textit{\textbf{X}}}) \mathbf {u}]^2} = 0. \end{aligned}$$This entails the following eigenvalue equation:
$$\begin{aligned} \left[ GC_\nu ({\textit{\textbf{X}}}) + GC_\nu ({\textit{\textbf{X}}})^{\intercal } \right] ^{-1} \left[ GC_{\nu ,b}({\textit{\textbf{X}}}) + GC({\textit{\textbf{X}}})_{\nu ,b}^{\intercal } \right] \mathbf {u} = \lambda \mathbf {u}. \end{aligned}$$ -
(ii)
The other option is to maximize the gross between-group variability as a share of the within-group one, i.e.
$$\begin{aligned} \mu := \frac{\mathbf {u}^{\intercal } GC_{\nu ,b}({\textit{\textbf{X}}}) \mathbf {u}}{\mathbf {u}^{\intercal } GC_{\nu ,w}({\textit{\textbf{X}}}) \mathbf {u}}, \end{aligned}$$then we get:
$$\begin{aligned} \frac{ [GC_{\nu ,b}({\textit{\textbf{X}}})+GC_{\nu ,b}({\textit{\textbf{X}}})^{\intercal }] \mathbf {u} \left[ \mathbf {u}^{\intercal } GC_{\nu ,w}({\textit{\textbf{X}}}) \mathbf {u} \right] - \left[ \mathbf {u}^{\intercal } GC_{\nu ,b}({\textit{\textbf{X}}}) \mathbf {u} \right] [GC_{\nu ,w}({\textit{\textbf{X}}}) + GC_{\nu ,w}({\textit{\textbf{X}}})^{\intercal }] \mathbf {u}}{[\mathbf {u}^{\intercal } GC_{\nu ,w}({\textit{\textbf{X}}}) \mathbf {u}]^2} = 0. \end{aligned}$$Therefore, a Mahalanobis metric in the Gini sense is obtained thanks to the following eigenvalue equation,
$$\begin{aligned} \left[ GC_{\nu ,w}({\textit{\textbf{X}}}) + GC_{\nu ,w}({\textit{\textbf{X}}})^{\intercal } \right] ^{-1} \left[ GC_{\nu ,b}({\textit{\textbf{X}}}) + GC({\textit{\textbf{X}}})_{\nu ,b}^{\intercal } \right] \mathbf {u} = \mu \mathbf {u}. \end{aligned}$$
\(\square \)
Proof of Proposition 3.2
From (8), since \({\bar{\mathbf {a}}}_{.\ell } = {\bar{\mathbf {f}}}_{.\ell } = 0\):
Therefore, the analysis of the variability between \(\mathbf {a}_{.\ell }\) and \(\mathbf {z}_{.k}\) is simply the study of the correlation between \(\mathbf {f}_{.\ell }\) and \(\mathbf {z}_{.k}\):
\(\square \)
Rights and permissions
About this article
Cite this article
Condevaux, C., Mussard, S., Ouraga, T. et al. Generalized Gini linear and quadratic discriminant analyses. METRON 78, 219–236 (2020). https://doi.org/10.1007/s40300-020-00178-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40300-020-00178-2