Repetitive Control Compensator Design for Frequency Response near Singularities

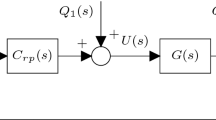
Abstract

Repetitive control (RC) aims to achieve zero error from a feedback control system that is subject to a periodic disturbance of known period, or that is executing a periodic command. It can be used in spacecraft for jitter mitigation, for creating active vibration isolation mounts that theoretically can produce complete cancellation of periodic jitter. RC is a feedback loop around an existing feedback control system that adjusts the control system’s command aiming for that command that produces zero error. The design requires creating a compensator that cancels the phase lag through the feedback controller within a tolerance of less that ±90 degrees. The phase behavior of digital systems is presented in detail, exhibiting the possibility of step discontinuities in phase that approach ± 90 degrees. The issue of whether stable RC systems can be designed for sample rates near such discontinuities is addressed. It is shown in numerical studies that compensators that use as few as 2 or 4 gains times previously recorded errors can be sufficient for not only stability, but can give rather fast convergence to zero error for nearly all frequencies except approaching Nyquist frequency. For systems with even pole excess, there can be a different kind of phase singularity that occurs as the sample rate tends to infinity. When designing for fast sample rate it is best to use a larger set of gains to obtain good convergence rate for all frequencies except approaching Nyquist. It was expected that these discontinuities might make it hard to design the RC compensators, but the results indicate that the singularities do not cause serious difficulty in RC design.

Appendix

(A) CONTINUOUS TO DISCRETE MAPPING

For simplicity, consider that the difference equation of the feedback control system, Eq. (1), came from discretizing a differential equation, represented by Laplace transfer function G(s), fed by a zero order hold. This implies that the feedback control system was a continuous time system, and its command is coming through a zero order hold so that the repetitive controller can feed updates based on stored data from the previous period. We assume that G(s) is asymptotically stable and minimum phase, and define its pole excess p_e as the number of poles minus the number of zeros. We are particularly interested in the zeros introduced in the discretization process. Although we assumed that the feedback control system was continuous time, note that if it was a digital control system instead, and the plant inside the loop is fed by a zero order hold of the signal coming out of the controller, the zeros introduced in that conversion of the plant will also be zeros of the closed loop digital control system.

The Pole Zero Mapping

One obtains the discrete time transfer function G(z) corresponding to difference equation Eq. (1) from G(s) according to

$$ G(z)=\left(\frac{z-1}{z}\right)\mathcal{Z}\left\{G(s)\frac{1}{s}\right\} $$

(17)

It is standard notation to let the Z represent taking the z-transform of the time domain signal it operates on, which can be specified if desired in terms the signals Laplace transform G(s)/s that represents the unit step response (starting at zero initial conditions), and the symbol $\mathcal{Z}$ indicates that this response is sampled at the same times, and then the z-transform is taken. Note that G(s)/s can be expanded in partial fractions as a sum of factors with denominators s and (s + p) where -p is a pole of G(s). It is ok for the pole to be complex. Then each factor can be converted according to: The s becomes z/(z − 1), and the (s + p) becomes z/(z − exp(−pT)). Put the sum of terms over a common denominator, note that the (z − 1) cancels. This avoids the need to actually find the time domain signal and sample it. We conclude that any pole of G(s) at -p is mapped precisely to its corresponding pole of G(z) according to

$$ z={e}^{- pT} $$

(18)

The numerator is collected after putting things over a common denominator, and one should expect the discrete time zero locations to depend on the pole locations. However, the zeros expanded in a Taylor series satisfy the same formula up through the order of the differential equation, i.e. the number of poles in G(s). Consider $G(s)=\frac{\left(s-a\right)}{\left(s-{b}_1\right)\left(s-{b}_2\right)}.$ One can calculate analytically the single zero location and expand to obtain the following zero location

$$ z=1+ aT+\frac{1}{2!}{a}^2{T}^2+\left[\frac{1}{4}{a}^3-\frac{1}{12}a\left(\left({b}_1+{b}_2\right)+2\left({b}_1^2+{b}_1{b}_2+{b}_2^2\right)\right)\right]{T}^3+\cdots $$

(19)

If T is small enough, the terms depending on the pole locations become negligible.

Zeros Introduced by the Discretization

When the forcing function of a differential equation comes through a zero order hold, there is a step change in the input at each time step, but physical systems do not have the output change instantaneously. One must wait until the next time step, i.e. sample time, before one sees the output change. Therefore, as in Eq. (1), the most recent change in the input on the right hand side of the equation must be one step behind the most up to date output on the left hand side of the equation (for any system with more poles than zeros). The implication is that G(z) must generically have one less zero than pole, and this should happen independent of how many zeros are in G(s) (we do not consider nonphysical systems with the same number in G(s), meaning that a step change in the input to the differential equation creates an instantaneous step change in the output).

Thus, if the pole excess of G(s) is 2, there will be one zero introduced, if it is 3, two zeros will be introduced, etc. These zeros are all on the negative real axis. Reference [29] derives the locations of these extra zeros in the limit as the sample time interval tends to zero. The results are given in Table 1. For odd pole excesses, the table lists the zeros introduced outside the unit circle. For each zero outside there is a corresponding zero introduced inside the unit circle asymptotically at the reciprocal location. For even pole excesses, there is a zero that is asymptotically located at −1 on the unit circle. Normally, when the sample rate is reduced this zero moves off the boundary and into the unit circle.

The Introduced Zeros as the Sample Time Interval Becomes Long

Consider the other limiting case, when the time interval between samples gets very long. Consider the differential equation at the start of a time step. There is an initial state defining a set of initial conditions. The step change in the input at the beginning of the time step causes the system to respond with transients, but if the step is long enough the differential equation will reach arbitrarily close to the steady state response of the system to the constant being applied during that time step. By the end of the time step, the initial conditions are forgotten. Therefore, the output seen at sample times is always the steady state response to the constant forcing function being applied during that step. Equation (2) reduces to

$$ Y(z)=\left(\frac{b_{r-1}{z}^{n-1}}{z^n}\right)U(z) $$

(20)

The conclusion is that as the sample time interval T increases from the limit used for Table 1, all zeros outside the unit circle will eventually move from outside the unit circle to inside the unit circle and converge to the origin. The passage of zeros from outside to inside the unit circle creates a singularity in the inverse problem addressed by RC, which is the subject of this paper.

(B) UNDERSTANDING THE FREQUENCY RESPONSE OF DISCRETE TIME SYSTEMS

The Linear Phase Lag of a Zero Order Hold

At the start of a time step with a zero order hold, the hold output is current. By the end of the time step the output is one time step old. This suggests that on the average, the output of a zero order hold is one half time step behind the input. There are two time steps per period at Nyquist frequency, so one half time step late corresponds to introducing an extra 90-degree phase delay. At half Nyquist, there are 4 time steps per period so one half time step corresponds to 45 degree phase delay. The one-half time step produces a phase delay that is linear with frequency from zero at DC and 90 degrees at Nyquist. Several figures given in the section that presents designs of compensators, demonstrate that to graphical accuracy, the plots of phase response of the original differential equation plus the extra linear phase lag of one-half time steps, lie on top of the discretized system phase response.

The match is not perfect, but very good for reasonable sample rates. To illustrate this, consider

$$ \frac{dy(t)}{dt}+2y(t)=2{y}_d=2t $$

(21)

The particular solution to this equation at the sample times is $\left( kT-\frac{1}{2}\right).$ If one converts Eq. (21) to equivalent difference equation using Eq. (17), with forcing function 2 t coming in through a zero order hold, the corresponding particular solution is given by

$$ \left[ kT-\left(\frac{T}{1-{e}^{-2T}}\right)\right] $$

(22)

where

$$ -\left(\frac{T}{1-{e}^{-2T}}\right)=\frac{-T}{1-\left[1-2T+\left(\frac{1}{2}\right){(2T)}^2-\cdots \right]}\approx -\frac{1}{2}\left(\frac{1}{1-T+\left(\frac{2}{3}\right){T}^2-\cdots}\right)\approx -\frac{1}{2}-\frac{1}{2}T+\frac{2}{3}{T}^2-\cdots $$

(23)

The first correction term – T/2 is the half time step delay, and the next correction term is $\frac{2}{3}{T}^2$ which can be quite small for common sample times. When sampling at 100 Hz sample rate, T² = 10⁻⁴, at 1000 Hz sample rate, T² = 10⁻⁶.

Comparison of Continuous and Discrete Frequency Response at High Sample Rates

Consider the properties of the steady state phase response of transfer functions G(s), i.e. the angle made by the complex number G(iω) with the positive real axis. The rules for Bode plots say that as ω → ∞ each real pole contributes −90 degrees, each real zero contributes +90 degrees, each complex conjugate pole pair contributes −180 degrees, and each complex conjugate zero pair contributes +180 degrees.

Therefore, if the pole excess is an odd number 1, 3, 5, … the phase as ω → ∞ is 90, 270, 450, ..., i.e. an odd pole excess implies a phase lag at high frequency that is an odd multiple of 90 degrees. But when the extra 90 degrees of the linear phase lag of the previous subsection is included, these phase lags are multiples of −180 degrees.

For even pole excesses 2, 4, 6, … the phase as ω → ∞ is −180, −360, −540 degrees. When the extra 90 degrees of the linear phase lag of the previous subsection is included, these phase lags become odd multiples of −90 degrees.

The phase response of G(z) is given by the angle of the complex number G(exp(iωT)) made with the positive real axis. The argument goes around the unit circle in the z-plane, and reaches Nyquist frequency when ωT = π or 180 degrees, i.e. for G(−1). Since the coefficients in G(z) are all real, G(−1) must be real and either positive or negative. This means that the phase angle at Nyquist must be a multiple of 180 degrees.

For a third order system with no zeros, the pole excess of 3 with linear phase lag produced a multiple of −180 degrees, and the discrete time phase had no trouble following the continuous time phase plus the linear phase lag. If the sample rate is chosen so that Nyquist occurs at frequencies after the continuous time phase lag is close to its ω → ∞ value, the discrete time phase only needs to make a small adjustment to reach its multiple of −180.

However, if it were a 4th order system, as the discrete time frequency response approaches Nyquist, the phase must deviate from the continuous time response with the linear phase lag, and aim for a multiple of −180 – making an adjustment that approaches ±90. This paper examines what difficulties this adjustment causes to the design of a repetitive control compensator.

Comparison of Continuous and Discrete Frequency Response at Lower Sample Rates

If a slower sample rate is chosen, then Nyquist frequency can occur at a frequency when the continuous time phase lag is still growing. Except in isolated cases, the continuous time phase lag together with the linear phase lag will not be at a multiple of −180 degrees. As the frequency approaches Nyquist, the discrete time plot must make a final move, either to the next multiple of −180 degrees above, or the next below. It is interesting to note that if it chooses to go up from some value near an odd multiple of −90 degrees, it could be choosing to cancel the linear phase lag we expect in the discrete time system which can seem counter-intuitive.

How to Visualize the Phase Contributions of Poles and Zeros

Consider a G(z) of the form

$$ G(z)=\frac{K\left(z-{z}_1\right)\left(z-{z}_2\right)}{\left(z-{p}_1\right)\left(z-{p}_2\right)\left(z-{p}_3\right)} $$

(24)

To find phase at frequency ω, substitute the point z = exp(iωT) on the unit circle into this expression, and find the angle made with the positive real axis. For a chosen ω, each term can be written as its magnitude times the exponential of its phase angle. The product of two terms, multiplies the magnitudes but adds the phase. A ratio of two terms produces a phase that is the phase of the numerator minus the phase of the denominator. Then the phase of G(z) is given by the sum of the phase angles of (exp(iωT) − z_j) for j = 1, 2, minus the sum of the phase angles for (exp(iωT) − p_j) for j = 1, 2, 3. Figure 4 shows the phase angles for a chosen ω for a zero outside the unit circle on the negative real axis, and a pole inside the unit circle. This plot makes it easy to visualize the contributions of each factor.

(C) GUIDING PRINCIPLES IN COMPENSATOR DESIGN

From Eq. (9) it would appear that the best possible repetitive control compensator is the system inverse G⁻¹(z), since it would create zero error immediately. However, from Table 1, it is clear that for perhaps most systems in the world, this aims to make zeros outside the unit circle into poles, creating unstable controllers. References [21, 26] address this problem by instead asking for a compensator the is the inverse of the steady state frequency response. This inverse is not unstable, and it should result in the error approaching zero asymptotically as time progresses. To implement this approach, one needs a way to compute a good approximation of the frequency response inverse that can be implemented easily. This is accomplished by designing an FIR filter

$$ {\displaystyle \begin{array}{c}F(z)={a}_1{z}^{m-1}+{a}_2{z}^{m-2}+\cdots +{a}_m{z}^0+\cdots +{a}_{n-1}{z}^{-\left(n-m-1\right)}+{a}_n{z}^{-\left(n-m\right)}\\ {}=\frac{a_1{z}^{n-1}+{a}_2{z}^{n-2}+\cdots +{a}_m{z}^{n-m}+\dots +{a}_{n-1}{z}^1+{a}_n{z}^0}{z^{\left(n-m\right)}}\end{array}} $$

(25)

that is applied to the error signal of the previous period. The z⁰ term is one period back, i.e. d time steps back, from the current time step k, and the z to positive powers indicate steps forward, and the negative powers indicate time steps backward from one period back. To apply this compensator in practice, one simple multiplies the appropriate coefficient times the error recorded in the previous period for the time step indicated, and adds up the results. This compensator consists of n − 1 zeros, and n − m poles at the origin. We will see that the compensator can produce stability and convergence to zero tracking error for a very small number of gains, like 2, 3 or 4. It can also be very effective at creating fast convergence. For a 7 degree of freedom model of each link of a robot at NASA Langley Research Center, use of 12 gains made the left-hand side of Eq. (9) less than 0.04 which is very far from the stability limit of unity, and indicates very fast learning with repetitions [27].

Reference [21] Considers Replacing the [1 − FG] of Optimization Function Eq. (11) by [F − G⁻¹]. This Minimization Can Be Converted to Eq. (12) by Introducing a Weighting Factor GG^∗, so that it Corresponds to a Different Weighting of the Importance of each Frequency. Another Approach Uses Taylor Series Expansions of each Factor, and the Result Places Compensating Zeros Evenly Spaced Precisely around a Circle of the Radius of the System Zero to Be Compensated [24, 26]. Reference [27] Improves on Reference [24] by Expanding the Products in Taylor Series Instead of the Individual Factors. Some People Want to Use a Different Norm for the Cost Functional. Reference [22] Addresses RC of Non-minimum Phase G(s), and Needs a Min-Max Cost Function to Get Good Learning at DC, but Finds that to Make Good Learning Overall One Needs to Transition Away from Min-Max as the Frequency Goes Up. Perhaps the most Common Design Approach Is Due to [8]. This Involves Using an IIR Filter to Cancel all System Zeros and Poles inside the Unit Circle, and Then Introducing a Zero inside the Unit Circle at the Location that Is the Reciprocal of the Zero outside, Placing a Pole at the Origin, and Tuning for DC Gain of One or Less for Minimum Phase G(s)