Skip to main content
SpringerLink
Log in

Robe’s Restricted Problem of 2 + 2 Bodies with a Roche Ellipsoid - Triaxial System

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

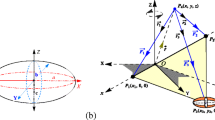
This paper investigates the motion of two infinitesimal masses on the location and stability of the equilibrium points in Robe’s restricted problem of 2 + 2 bodies with the bigger primary a Roche ellipsoid and the smaller a triaxial body. We suppose the bigger primary of mass m 1 to be filled with a homogeneous incompressible fluid of density ρ 1. The third and the fourth bodies (of mass m 3 and m 4 respectively) are small solid spheres of density ρ 3 and ρ 4 respectively inside the ellipsoid, with the assumption that the mass and the radius of the third and the fourth body are infinitesimal. We assume that m 2 is describing a circle around m 1. The masses m 3 and m 4 mutually attract each other, do not influence the motion of m 1 and m 2 but are influenced by them. We have taken into consideration all the three components of the pressure field in deriving the expression for the buoyancy force viz (i) due to the own gravitational field of the fluid (ii) that originating in the attraction of m 2 (iii) that arising from the centrifugal force. In this paper, equilibrium solutions of m 3 and m 4 and their linear stability are analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Abdulraheem, A, Singh, J.: Combined effects of perturbation, radiation and oblateness on the stability of equilibrium points in the restricted three-body problem. Astron. J. 131, 1880–1885 (2006)

    Article  Google Scholar 

  2. Abdul Raheem, A, Singh, J.: Combined effects of perturbations, radiation and oblateness on the periodic orbits in the restricted three-body problem. Astrophys Space Sci. 317, 9–13 (2008). https://doi.org/10.1007/s10509-008-9841-4

    Article  Google Scholar 

  3. Kaur, B, Aggarwal, R: Robe’s restricted problem of 2 + 2 bodies when the bigger primary is a Roche ellipsoid. Acta Astronaut. 89, 31–37 (2013). https://doi.org/10.1016/j.actaastro.2013.03.022. ISSN 0094–5765

    Article  Google Scholar 

  4. Brouwer, D., Clemence, G.M.: Methods of Celestial Mechanics. Academic Press, New York (1961)

    MATH  Google Scholar 

  5. Chandrashekhar, S.: Ellipsoidal Figures of Equilibrium (Chapter 8). Dover Publication Inc, New York (1987)

    Google Scholar 

  6. Croustalloudi, M.N., Kalvouridis, T.J.: The Restricted 2 + 2 Body Problem: Parametric Variation of the Equilibrium States of the Minor Bodies and Their Attracting Regions. ISRN Astron. Astrophys. 281849, 15 pages (2013)

    Google Scholar 

  7. Hallan, P.P., Mangang, K.B.: Existence and linear stability of equilibrium points in the Robe’s Restricted Three-Body Problem when the first primary is an Oblate Spheroid. Planet. Space Sci. 55, 512–516 (2007)

    Article  Google Scholar 

  8. Kaur, B, Aggarwal, R.: Robe’s problem: Its extension to 2 + 2 bodies. Astrophys. Space Sci. 339, 283–294 (2012)

    Article  MATH  Google Scholar 

  9. Kaur, B, Aggarwal, R: Robe’s restricted problem of 2 + 2 bodies when the bigger primary is a Roche ellipsoid and the smaller primary is an oblate body. Astrophys. Space Sci. https://doi.org/10.1007/s10509-013-1607-y. ISSN 0004-640X (2013)

  10. Plastino, AR, Plastino, A: Robe’s restricted three-body problem revisited. Celest. Mech. Dynam. Astron. 61, 197–206 (1995)

    Article  MATH  Google Scholar 

  11. Robe, HAG: A new kind of three-body problem. Celest. Mech. 16, 343–351 (1977)

    Article  MATH  Google Scholar 

  12. Wikipedia: Roche Limit, Wikipedia (2012)

  13. Shrivastava, A. K., Garain, D.: Effect of perturbation on the location of libration point in the Robe restricted problem of three bodies. Celest. Mech. Dyn. Astr. 51, 67–73 (1991)

    Article  MATH  Google Scholar 

  14. Mohammed, H.L.: Robe’s circular restricted three-body problem under oblate and triaxial primaries, vol. 109 (2012)

  15. Singh, J, Oni, L.: Effect of oblateness, perturbations, radiation and varying masses on the stability points in the R3BP. Astrophys. Space Sci. 344(1), 51–61 (2012). https://doi.org/10.1007/s/10509-012-1324y

    Article  MATH  Google Scholar 

  16. Singh, J., Sandah, A.U.: Existence and linear stability of equilibrium points in the Robe’s restricted three-body problem with oblateness. Adv. Math. Phys. 2012, 18 pages (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Singh, J., Mohammed, H.L.: Out-of-plane equilibrium points and their stability in the Robe’s problem with oblateness and triaxiality. Astrophys. Space Sci. 345, 265–271 (2013)

    Article  MATH  Google Scholar 

  18. Singh, J., Omale, A.J., Cyril Okeme, V.: Robe’s circular restricted three-body problem with a Roche ellipsoid-triaxial versus oblate system. Astrophys. Space Sci. 351, 119–124 (2014)

    Article  Google Scholar 

  19. Singh, J, Balogun, EA: Stability of triangular points in the photogravitational CR3BP with Poynting-Robertson drag and a smaller triaxial primary. Astrophys. Space Sci. (2014) https://doi.org/10.1007/s10509-014-2023-7 ISSN 0004-640X

  20. Sterne, T.E.: An Introduction to Celestial Mechanics. Interscience Tracts on Physics and Astronomy. Interscience Publishers (1960)

  21. Umar, A, Singh, J: Semi-analytic solutions for the triangular points of double white dwarfs in the ER3BP: Impact of the body’s oblateness and the orbital eccentricity. Adv. Space Res. (2015). https://doi.org/10.1016/j.asr.2015.01.042

  22. Whipple, A.L.: Equilibrium solutions of the restricted problem of 2 + 2 bodies. Celest. Mech. 33, 271–294 (1984)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Sri Aurobindo College, University of Delhi, Delhi, India

    Rajiv Aggarwal

  2. Lady Shri Ram College for Women, University of Delhi, Delhi, India

    Bhavneet Kaur

  3. Maharaja Agrasen College, University of Delhi, Delhi, India

    Sushil Yadav

Authors
  1. Rajiv Aggarwal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bhavneet Kaur
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sushil Yadav
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bhavneet Kaur.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aggarwal, R., Kaur, B. & Yadav, S. Robe’s Restricted Problem of 2 + 2 Bodies with a Roche Ellipsoid - Triaxial System. J of Astronaut Sci 65, 63–81 (2018). https://doi.org/10.1007/s40295-017-0119-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40295-017-0119-3

Keywords

Search

Navigation