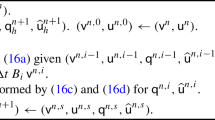Introduction

Consider a natural second order differential equation of the form:

$$ \ddot{\textit{\textbf{r}}}=\textbf{g}\left( t,\textit{\textbf{r}},\dot{\textit{\textbf{r}}}\right) $$
(1)

where r is an n-vector of position coordinates, \(\dot {\textit {\textbf {r}}}\) is an n-vector of velocity coordinates. The essence of Lambert’s problem is to find the initial velocity (\(\dot {\textit {\textbf {r}}}_{0}(t_{0})=\textit {\textbf {v}}_{0}\)) such that solving the initial value problem with the initial boundary conditions (r 0, v 0 at t 0) gives a trajectory that reaches the final position (r f ) at the given final time (t f ). In the case of Keplerian motion, the solution for the fraction-of-an-orbit case is known to be unique except for the cases that the initial and final vectors (r 0, r f ) are co-linear [1]. For multi-orbit transfers, the solution is not unique; however, all solutions can be reliably computed except near the co-linear special cases. For the specific case of analytically tractable Keplerian motion, solving the TPBVP can be reduced to finding the roots of a scalar nonlinear algebraic equation, and has been the subject of almost two centuries of refinements culminating in the elegant solution of R. H. Battin [1]. Ochoa and Prussing [2] further refined this work to produce a nice algorithm that finds the multiple solutions to the Keplerian problem. We mention this algorithm in more detail later in the paper.

The classical solution to the generalized (perturbed) Lambert’s problem, for a general right hand side of Eq. 1, involves a Newton iteration method whereby we require the n × n partial derivatives of the terminal position with respect to the initial velocity [∂ r(t f ) /∂ v(t 0)] to satisfy the 2n × 2n differential equations (2). [∂ r(t f ) /∂ v(t 0)] is the final time computation of the upper right n × n sub-matrix of the state transition matrix Φ(t, t 0).

$$ \dot{\Phi}(t,t_{0})=\left[\begin{array}{cc} 0 & I\\ \partial\textbf{g}/\partial\textbf{r} & \partial\textbf{g}/\partial\dot{\textbf{r}} \end{array}\right]{\Phi}(t,t_{0}),\;{\Phi}(t_{0},t_{0})=I. $$
(2)

To implement the classical shooting method these 4n 2 differential equations (2), coupled to the 2n equations of Eq. 1, results in 4n 2 + 2n differential equations that must be solved iteratively with the initial velocity updated following each iteration using a multi-dimensional Newton method (shooting method):

$$ \dot{\textit{\textbf{r}}}_{k+1}(t_{0})=\dot{\textit{\textbf{r}}}_{k}(t_{0})+{\Phi}_{21_{k}}^{-1}(t_{f},t_{0})\left\{ \textit{\textbf{r}}_{k}(t_{f})-\textit{\textbf{r}}_{f}\right\} ;\; k=1,2,... $$
(3)

The k subscript denotes the solution of Eqs. 1 and 2 with the k th iterative trial value for the unknown initial velocity vector \(\dot {\textit {\textbf {r}}}_{0}(t_{0})=\textit {\textbf {v}}_{0}\). For sufficiently close starting iteration, one can expect convergence in a single digit number of iterations. However, obtaining a sufficiently close starting estimate is not always easy and that is part of the challenge for each physical problem. This is especially acute for the case of multi-revolution orbit transfers where there are more than one feasible transfer orbit. In many cases, approximate versions of the governing differential equations, for example Battin’s [1] analytical two-body solution of Lambert’s problem, are used to initiate iterations for the fully perturbed system. Battin’s formulation generates all solutions, including the multiple revolution local roots. Utilizing the most attractive of the Keplerian starting iteratives is virtually always good enough for weakly perturbed orbit mechanics problems. When the perturbations are too large for convergence with the analytical two-body Lambert starting approximation, a homotopic method can frequently be used to sweep a parameter that gradually departs from a known solution to solve the fully perturbed problem at hand. However, in the presence of a general right hand side of Eq. 1, and a poor starting estimate, the problem is more challenging, and each iteration has to pay the overhead associated with computing the partial derivatives by solving Eq. 2.

Two alternative methods for solving the perturbed Lambert’s problem are the TPBVP implementation of modified Chebyshev-Picard iteration (MCPI) [3, 4], and the MCPI-TPBVP algorithm regularized using the Kustaanheimo-Stiefel time transformation [5, 6]. The first method converges over a small fraction of an orbit (about a third of an orbit depending on eccentricity) and the second method converges up to about 90% of an orbit. In this paper we present a third method for solving the perturbed Lambert’s problem; a local linearity-based approach that converges over multiple revolutions. It is attractive as there is no need to compute a state transition matrix and thereby we avoid solving the n × n differential equations (2). This alternate shooting technique is known as the method of particular solutions (MPS), as developed in by Miele [7]. We combine MPS with the MCPI initial value problem (MCPI-IVP) integration method to solve the perturbed two-body orbital equations of motion accurately and efficiently over multiple revolutions.

The motivation for this work is to respond to the orbital debris problem. There are over 500 USA-launched spent rocket boosters in low Earth orbit, and these are hazardous to operational satellites. Reducing the probability of collision is possible by orbit debris rendezvous, capture and de-orbit missions directed at the most high priority objects. The spent rocket boosters are attractive objects to remove because they all represent potential collisions and removing large objects has been shown to be one of the best ways to mitigate debris growth. Simulating hundreds of thousands of transfer orbits (Lambert problems) accurately and efficiently is essential for aiding in the solution to this debris removal problem. The algorithms we have developed using the methods described above can be used for designing and simulating missions to retrieve these objects, thus reducing the predicted future growth of orbital debris.

Modified Chebyshev-Picard Iteration

Modified Chebyshev Picard Iteration differs from the well-known step integrators such as Gauss-Jackson, Runge-Kutta-Nystrom and ODE45 in that it is a path approximation numerical integrator rather than a step-by-step integrator. Long state trajectory arcs are approximated continuously and updated at all time instances on each iteration.

The MCPI technique combines Picard iteration with the orthogonal Chebyshev polynomials. Emile Picard observed that any first order differential equation

$$ \frac{d\textit{\textbf{x}}(t)}{dt}=\textit{\textbf{f}}(t,\textit{\textbf{x}}(t)),\;\;\;\;t\,\epsilon\,[t_{0},t_{f}], $$
(4)

with an initial condition x(t 0) = x 0 and any integrable right hand side may be rearranged, without approximation, to obtain the following integral equation:

$$ \textit{\textbf{x}}(t)=\textit{\textbf{x}}(t_{0})+{\int}_{t_{0}}^{t}f(\mathbf{\tau},\textit{\textbf{x}}(\mathbf{\tau})) d\mathbf{\tau}. $$
(5)

A sequence of approximate solutions x i(t), (i = 1, 2, 3 ... , ∞), of the true solution x(t) that satisfies this differential equation may be obtained through Picard iteration using the following Picard sequence of approximate paths {x 0(t), x 1(t),..., x i−1(t), x i(t),...}:

$$ \textit{\textbf{x}}^{i}(t)=\textit{\textbf{x}}(t_{0})+{\int}_{t_{0}}^{t}f(\mathbf{\tau},\textit{\textbf{x}}^{i-1}(\mathbf{\tau}))d\mathbf{\tau},\;\;\; i=1,2,... $$
(6)

Picard proved that for smooth, differentiable, single-valued nonlinear functions f(t, x(t)), there is a time interval |t f − t 0| < δ and a starting trajectory x 0(t) satisfying ∥x 0(t) − x(t)∥ ∞ < ∞, that for suitable finite bounds (δ, Δ), the Picard sequence of trajectories represents a contraction operator that converges to the unique solution of the initial value problem. The rate of convergence is typically geometric. The guaranteed convergence property sets this method apart from other approaches. The numerical accuracy and efficiency are dominated by the particular process used to carry out the integral; note since the previous (i − 1) trajectory approximation is known, the integrand is considered a function of time only. Chebyshev polynomials are used for approximating the integrand in the Picard iteration sequence, and these orthogonal polynomials integrate to produce a Chebyshev series for the integral, including the imposition of initial (or final) boundary conditions.

The original fusion of orthogonal approximation theory and Picard iteration was introduced by Clenshaw and Norton in 1963 [8]. Feagin published his PhD dissertation [9] in 1972 on Picard iteration using Chebyshev approximation. He established the first vector-matrix version of Picard iteration utilising orthogonal basis functions [10]. In 1980 Shaver wrote a related dissertation giving insights on parallel computation using Picard Iteration and Chebyshev approximation [11]. In 1997 Fukushima [12] addressed parallelization of Picard iteration in a particular computer architecture. His results showed that a particular parallel implementation of his algorithm did not give the theoretical speedup he anticipated.

A decade later Bai and Junkins revisited this approach and developed improved algorithms for solving IVPs and TPBVPs [3, 13]. They established new convergence insights and also developed vector-matrix formulations for solving initial and boundary value problems. These are published in Bai’s PhD dissertation [4]. Bani Younes and Junkins followed this work with methods to include high order gravity perturbations in order to more accurately represent the motion of satellites orbiting in the vicinity of the Earth [14,15,16]. Macomber and Junkins developed enhancements that took advantage of the “fixed-point” convergence nature of MCPI and allowed solutions to the perturbed two-body problem to be computed using variable fidelity force models and radially adaptative gravity approximations. They also made use of warm and hot starts for solving the perturbed problem [17, 18]. These enhancements resulted in substantial increases in the efficiency of MCPI while maintaining machine precision accuracy.

Method of Particular Solutions

The method of particular solutions is a local-linearity based approach that makes use of a reference trajectory \(\textit {\textbf {r}}_{ref}(t),\dot {\textit {\textbf {r}}}_{ref}(t),\ddot {\textit {\textbf {r}}}_{ref}(t)\) and a set of particular solutions. All neighboring solutions of Eq. 1 (reference and particular) can be re-formulated exactly in terms of a departure motion Δr(t) as

$$ \textit{\textbf{r}}(t)=\textit{\textbf{r}}_{ref}(t)+\triangle\textit{\textbf{r}},\;\;\dot{\textit{\textbf{r}}}(t)= \dot{\textit{\textbf{r}}}_{ref}(t)+\triangle\dot{\textit{\textbf{r}}},\;\;\ddot{\textit{\textbf{r}}}(t)= \ddot{\textit{\textbf{r}}}_{ref}(t)+\triangle\ddot{\textit{\textbf{r}}}. $$
(7)

From Eqs. 7 and 1, we can write the exact departure motion differential equation:

$$ \triangle\ddot{\textit{\textbf{r}}}=\textit{\textbf{g}}\left( t,\textit{\textbf{r}}_{ref}(t)+\triangle\textit{\textbf{r}},\dot{\textit{\textbf{r}}}_{ref}(t)+\triangle\dot{\textit{\textbf{r}}}\right)+\textit{\textbf{u}}-\ddot{\textit{\textbf{r}}}_{ref}(t). $$
(8)

Now consider the circumstance that \(\ddot {\textit {\textbf {r}}}_{ref}(t)\) is a solution of the differential equation which satisfies “good” initial boundary conditions; in this case, the Δ’s can be expected to be small, \(\ddot {\textit {\textbf {r}}}_{ref}(t)=\textit {\textbf {g}}\left (t,\textit {\textbf {r}}_{ref}(t),\dot {\textit {\textbf {r}}}_{ref}(t)\right )\) and to a linear approximation, the exact nonlinear Eq. 8 could be replaced by an approximate linear equation of the form

$$ \triangle\ddot{\textit{\textbf{r}}}=A\triangle\textit{\textbf{r}}+B\triangle\dot{\textit{\textbf{r}}}+ O(\triangle^{2}). $$
(9)

where A, B are time varying Jacobians of g with respect to \(\textit {\textbf {r}},\dot {\textit {\textbf {r}}}\) evaluated along r r e f (t). We can consider the departure motion linear as long as it is to within the accuracy that the linear Eq. 9 approximates the exact departure motion of Eq. 8. Note, the reference trajectory is not generally held invariant, so the initial conditions can be updated to reflect improved knowledge after each successful iteration. Consider the case that the reference motion satisfies the known left position coordinates exactly r r e f (t 0) = r 0, and the initial velocity \(\dot {\textit {\textbf {r}}}_{ref}(t_{0})\) represents the current best estimate of the unknown initial velocity. For this given (or just computed) r r e f (t), consider three variant trajectories obtained by varying the initial velocity by small linearly independent (typically orthogonal) perturbations. Typically, initial perturbations occur in the last three significant digits of the motion; for example if the numerical solution is accurate to 10 digits, the norm of the typical independent initial condition perturbations could be \(\left |{\Delta }\dot {\textit {\textbf {r}}}_{j}(t_{0})\right |\approx 10^{-7}\left |\dot {\textit {\textbf {r}}}_{ref}(t_{0})\right |\) to obtain the neighboring initial velocities:

$$ \textit{\textbf{r}}_{j}(t_{0})=\textit{\textbf{r}}_{ref}(t_{0})=\textit{\textbf{r}}_{0};\;\; \dot{\textit{\textbf{r}}}_{j}(t_{0})=\dot{\textit{\textbf{r}}}_{ref}(t_{0})+\triangle\dot{\textit{\textbf{r}}}_{j} (t_{0});\;\; j=1,2,3. $$
(10)

Next solve the differential Eq. 1 for each of the three particular solutions r j (t). Now we can form the exact departure motions

$$ \triangle\textit{\textbf{r}}_{j}(t)=\textit{\textbf{r}}_{j}(t)-\textit{\textbf{r}}_{ref}(t). $$
(11)

These exact departure motions are particular solutions and conjectured to approximately satisfy the linear differential equation in Eq. 9. Since independent velocity initial conditions were used it is assumed that these trajectories span the space of interest along with all neighboring trajectories of interest that also satisfy the linear departure motion Eq. 9. The linear combination of any particular solution of a linear differential equation satisfies the differential equation as well, and the general solution as a linear combination of three (in general n) departure motions can be written as shown in Eq. 12.

$$ \triangle\textit{\textbf{r}}(t)\approx\underset{j=1}{\overset{3}{\sum}}\alpha_{j}\triangle\textit{\textbf{r}}_{j}(t) \Rightarrow\textit{\textbf{r}}(t)\approx\textit{\textbf{r}}_{ref}(t)+\underset{j=1}{\overset{3}{\sum}}\alpha_{j} \triangle\textit{\textbf{r}}_{j}(t) $$
(12)

If the Δ’s exist rigorously in the linear domain, of course, Eq. 12 would hold with negligible error. Here we consider only 3 variant trajectories because the admissible initial variations are only the unknown initial velocity coordinates. That is, we constrain r j (t 0) = r r e f (t 0) and Δr j (t 0) = 0.

Figure 1 shows shows a conceptual example of the departure motion for the three particular solutions. Notice that r B (t f ), the target position, lies at the vertex of the 3-D parallelpiped, which is a scaled (with respect to α) version of the space spanned by Δr j ; the r B (t f ) is approximated (to within the assumption of linearity) from the linear combination of the three α j Δr j . For the case shown, all three α j ’s are less than 1, but the general requirement is that the current miss vector Δr B = r B (t f ) − r r e f (t f ) lies in the region approximated by Eq. 9.

Fig. 1
figure 1

Departure motion space for the method of particular solutions. Δr 1, Δr 2 and Δr 3 are position vectors from r r e f (t f ) to r 1(t f ), r 2(t f ) and r 3(t f ) respectively

Full size image

Evaluating Eq. 12 at the final time and imposing the desired result that r(t f ) = r f , leads to the solution for the coefficients of linear combination

$$ \left\{ \begin{array}{c} \alpha_{1}\\ \alpha_{2}\\ \alpha_{3} \end{array}\right\} \approx\left[\begin{array}{ccc} \triangle\textit{\textbf{r}}_{1}(t_{f}) & \triangle\textit{\textbf{r}}_{2}(t_{f}) & \triangle\textit{\textbf{r}}_{3}(t_{f}) \end{array}\right]^{-1}\left\{ \textit{\textbf{r}}_{B}(t_{f})-\textit{\textbf{r}}_{ref}(t_{f})\right\} $$
(13)

Given the α i s, we can compute the departure △r(t) and the time derivatives at any time t.

$$ \triangle\textit{\textbf{r}}(t_{f})=\alpha_{1}\triangle\textit{\textbf{r}}_{1}(t_{f})+\alpha_{2}\triangle \textit{\textbf{r}}_{2}(t_{f})+\alpha_{3}\triangle\textit{\textbf{r}}_{3}(t_{f}), $$
(14)
$$ \triangle\dot{\textit{\textbf{r}}}(t_{f})=\alpha_{1}\triangle\dot{\textit{\textbf{r}}}_{1}(t_{f})+\alpha_{2}\triangle \dot{\textit{\textbf{r}}}_{2}(t_{f})+\alpha_{3}\triangle\dot{\textit{\textbf{r}}}_{3}(t_{f}). $$
(15)

The velocity departure equation obviously holds at time t 0, so the time derivative of Eq. 13, evaluated at time t 0, allows a new estimate for the initial velocity to be calculated.

$$ \dot{\textit{\textbf{r}}}_{new}(t_{0})=\dot{\textit{\textbf{r}}}_{ref}(t_{0})+\underset{j=1}{\overset{3}{\sum}} \alpha_{j}\triangle\dot{\textit{\textbf{r}}}_{j}(t_{0}). $$
(16)

We mention that occasionally the volume shown in Fig. 1 can collapse into a plane, and in extreme cases into a line as a consequence of the particular sensitivities of the local position variations. While rare, these rank deficiencies can be overcome in several ways. The decision to use three orthogonal independent velocity variations at t 0 is heuristically reasonable, but not a constraint. Instead, we can introduce sets of random initial velocity variations. We are also not constrained to use only three particular solutions if a rank deficiency in Eq. 16 is encountered. If n > 3 particular solutions are generated, then in lieu of Eq. 13, we can determine the smallest \({\Sigma \alpha ^{2}_{j}}\) satisfying

$$ \textit{\textbf{r}}(t_{f})=\textit{\textbf{r}}_{ref}(t_{f})+\underset{j=1}{\overset{n}{\sum}}\alpha_{j} \triangle\textit{\textbf{r}}_{j}(t_{f}). $$
(17)

Given an invertible matrix in Eq. 13, Eq. 1 can now be re-solved with the reference trajectory’s initial velocity replaced by \(\dot {\textit {\textbf {r}}}_{new}(t_{0})\). The procedure is repeated to compute three reference neighboring trajectories which will result in new α’s. We iterate for improved α’s using Eqs. 13 and 16, analogous to Newton’s method, but without the necessity of the partials \(\frac {\partial \mathbf {r}}{\partial \dot {\mathbf {r}}_{0}}\) (from computing a state transition matrix).

Any numerical integrator can be used for solving two-point boundary problems with MPS, however using MCPI affords an avenue for increased efficiency that is not available with other step-by-step integrators. We take advantage of the path approximation nature of MCPI (that is, nodes iteratively converge to fixed points in space) and utilize a variable fidelity force model for propagating the reference trajectory as described in Macomber’s dissertation [17]. Since the particular solutions lie close to the reference trajectory (within the linear domain), the following approximation for computing the acceleration for the particular solutions is made.

$$\begin{array}{@{}rcl@{}} \mathbf{a}_{particular} = \mathbf{a}_{particular_{low}} + {\Delta}\mathbf{a}_{reference}, \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \mathbf{a}_{particular_{low}} = \mathbf{a}_{particular_{(TB+ J_{2}+ J_{3}+ J_{4}+ J_{5}+ J_{6})}}, \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} {\Delta}\mathbf{a}_{reference} = \mathbf{a}_{reference_{40\times40}} - \mathbf{a}_{reference_{low}}. \end{array} $$
(20)

The particular solutions are then assumed to lie close to the reference trajectory, and their accelerations may be approximated at any node using

$$\begin{array}{@{}rcl@{}} \mathbf{a}_{approx_{particular}}(\textit{\textbf{r}}) &=& \mathbf{a}_{TB_{particular}}(\textit{\textbf{r}}) + \mathbf{a}_{(J_{2} + J_{3} + J_{4} + J_{5} + J_{6})_{particular}}(\textit{\textbf{r}})\\ &&+ (\mathbf{a}_{full_{particular}}(\textit{\textbf{r}}) - \mathbf{a}_{low_{particular}}(\textit{\textbf{r}})) + H.O.T. \end{array} $$
(21)

Remarkably, we demonstrate that computing the particular solutions with only low fidelity approximation function evaluations, that is, two-body plus zonal perturbations plus the difference between the full force evaluation and two-body plus zonal perturbations on the reference trajectory, greatly increases the efficiency of the algorithm while maintaining machine precision accuracy. Later we show that solving the perturbed Lambert’s problem using MPS with MCPI is about an order of magnitude faster compared with the classical shooting method and a tenth-twelfth order Runga-Kutta (RK(12)10) integrator. The RK(12)10 algorithm was shared by Feagin and Gottlieb [19].

Keplerian Lambert Solver

We now discuss an analytic method for solving the Keplerian TPBVP [2]. For the TPBVP, the initial position vectors (r 1 and r 2) and time of flight (t d e s i r e d ) are known, but what is unknown is the initial velocity \((\dot {\textit {\textbf {r}}}_{1})\) that is required to reach the final position in the desired time interval. General TPBVP shooting methods require a guess for the initial velocity to propagate the trajectory forward over the desired time interval. The miss distance between the current final position and the desired final position is used to refine the initial velocity guess, and the propagation is repeated iteratively until convergence. In contrast, the Keplerian solver used in this paper requires an initial guess for a (semimajor axis), and assuming two-body motion, the resulting trajectory will always terminate at the desired final position. However, the time of arrival is uncertain and it is unlikely that the initial guess for a would allow the spacecraft to arrive at the desired time. The error in the flight time, based on its sensitivity to a, is what must be iterated in order to determine the correct value of a that corresponds to the desired time of flight.

Ochoa and Prussing [2] provides a comprehensive mathematical explanation of Lambert’s problem, and develops the following transcendental equation that must be iterated via Newton’s method to solve for a corresponding to t d e s i r e d .

$$ \sqrt{\mu}t_{des}=a^{3/2}\left( \alpha-\beta-\left( \sin\left( \alpha\right)-\sin\left( \beta\right)\right)\right), $$
(22)

where α and β are given by Eqs. 23 and 24 respectively, and μ is the gravitational parameter. The parameters c and s are the chord and semiperimeter and are defined in Prussing’s paper [2].

$$ \sin\left( \frac{\alpha}{2}\right)=\left( \frac{s}{2a}\right)^{1/2}. $$
(23)
$$ \sin\left( \frac{\beta}{2}\right)=\left( \frac{s-c}{2a}\right)^{1/2}. $$
(24)

When solving Lambert’s problem there exists a minimum semimajor axis \(\left (a_{m}=\frac {s}{2}\right )\) associated with the minimum energy orbit transfer, and any transfer with a semimajor axis less that a m will result in an orbit that does not have enough energy to hit the desired target position. Prussing suggests a good initial guess for starting the iterations would be a = 1.001a m , with careful attention (see discussion below and Fig. 5) to ensure that all 2N + 1 solutions are obtained along all relevant solution branches for the multiple revolution case.

The time of flight associated with this minimum energy transfer is computed as follows:

$$ \sqrt{\mu}t_{m}=\left( \frac{s^{3}}{8}\right)^{1/2}\left( \alpha_{m}-\beta_{m}+\sin\left( \beta_{m}\right)\right), $$
(25)

where α m = π and \(\sin \left (\frac {\beta _{m}}{2}\right )=\left (\frac {s-c}{s}\right )^{1/2}\). For 0 ≤ θ ≤ π, \(\beta _{m}=\beta _{m_{0}}\) and for π ≤ θ ≤ 2π, \(\beta _{m}=-\beta _{m_{0}}\), where β m0 is the principal value of the sin−1 function. As discussed in Ochoa and Prussing [2], α and β are closely related to eccentric anomaly E 2 and E 1 at times t 1 and t 2 by a constant offset and therefore α − β = E 2 − E 1, and α > β. In addition to t m (transfer time corresponding to minimum energy ellipse) there is also the minimum time in which the elliptic transfer can be made. This is denoted as t p , or the parabolic transfer time.

$$ \sqrt{\mu}t_{p}=\frac{\sqrt{2}}{3}\left( s^{3/2}-sgn(\sin(\theta))(s-c)^{3/2}\right), $$
(26)

where the signum function, which is defined in Eq. 27, takes care of the sign change for transfer angles of θ < π to θ > π.

$$ sgn(x)=\left\{ \begin{array}{c} 1\;\;\;for\;x>0\\ -1\;\;\;for\;x<0 \end{array}\right.. $$
(27)

To summarize, Eq. 22 can be used to compute all elliptic transfers in the range 0 ≤ θ ≤ 2π where the values of α and β are determined from the principle values as follows:

$$ 0\leq\theta\leq\pi,\;\;\;\;\beta=\beta_{0}, $$
(28)
$$ \pi\leq\theta\leq2\pi,\;\;\;\;\beta=-\beta_{0}, $$
(29)
$$ t_{des}\leq t_{m},\;\;\;\;\alpha=\alpha_{0}, $$
(30)
$$ t_{des}>t_{m},\;\;\;\;\alpha=2\pi-\alpha_{0}. $$
(31)

To demonstrate the algorithm we show two example transfers that start at the same point on the departure orbit (blue) and terminate at the same point on the arrival orbit (red), but each transfer has a different specified time of flight and a different semimajor axis (Fig. 2). Figure 3 shows a dashed curve that is a Eq. 22 swept for various a values. This figure is easily generated in the forward direction (given r 1, r 2, θ or s, and sweeping over values of interest larger than a m , while computing α and β from Eqs 23 and 24). Note that the two branches that are separated by t m . The two orbit transfers shown in Fig. 2 lie on different branches of the curve shown in Fig. 3. The solution on the lower branch has a shorter time of flight and was computed with α = α 0 (obtained by adopting the principle value from Eq. 23 with \(\alpha _{0}=2\sin ^{-1}(\frac {s}{2a}),\,<\pi \)), whereas the solution on the upper branch has a longer time of flight and was computed with α = 2π − α 0.

Fig. 2
figure 2

Two example transfers computed for a transfer maneuver between two low Earth orbits. Note that one distance unit (DU) is one Earth radii

Full size image
Fig. 3
figure 3

Transfer time as a function of semimajor axis for transfers between two specific points on two different low Earth orbits. Note that one distance unit (DU) is one Earth radii

Full size image

Multiple Revolution Solutions

When the desired time of flight is long enough for the transfer orbit to make one or multiple complete revolutions of the focus (θ ≥ 2π) we find that the solution to Lambert’s problem is no longer unique, and in fact there are 2N + 1 distinct solutions to the problem (Fig. 4). As before, the semimajor axis is related to the desired time of flight through the following transcendental equation that differs only from Eq. 22 in that there is an additional term of 2N π added in the parenthesis.

$$ \sqrt{\mu}t_{des}=a^{3/2}\left( 2N\pi+\alpha-\beta-\left( \sin\left( \alpha\right)-\sin\left( \beta \right)\right)\right) $$
(32)
Fig. 4
figure 4

Multiple solutions for transferring between the same point on the departure orbit (blue) to the same point on the arrival orbit (red), in the same specified time of flight

Full size image

Figure 5 shows the time of flight as a function of sweeping the semimajor axis over a certain range for different values of N. Note that on each curve for which N > 0 there is a minimum possible transfer time (t m i n N ) which is marked by the blue dots. As expected, there is no minimum time-of-flight for the N = 0 case because as the time is decreased the orbit will eventually switch from an elliptic transfer to a parabolic transfer.

Fig. 5
figure 5

Time of flight as a function of semimajor axis for transfers between the two orbits shown in Fig. 4. All five orbit transfers occur in the same time of flight but have different values of semimajor axis. The three dashed black curves represent solutions for the N = 0 case (lower curve), N = 1 (middle curve) and N = 2 (upper curve). In this example N = 2 and we expect 2N + 1 = 5 solutions

Full size image

The value of \(t_{m_{N}}\) (33) that corresponds to the minimum energy orbit with semimajor axis \(\left (a_{m}=\frac {s}{2}\right )\) is marked by the red dots in Fig. 5. This value is critical to the solution process for isolating the multiple roots because it separates each curve into an upper and lower branch, each of which contains a solution.

$$ \sqrt{\mu}t_{m_{N}}=\left( \frac{s}{2}\right)^{3/2}\left( \left( 2N+1\right)\pi-\beta_{m}+\sin \left( \beta_{m}\right)\right). $$
(33)

To start the solution process the value of N m a x must be determined. This is done by root solving f(a) = 0 (34) with different values of N > 0. The function f(a) is given by

$$\begin{array}{@{}rcl@{}} f\left( a\right)&=&\left( 6N\pi+3\left( \alpha-\beta\right)-\left( \sin\left( \alpha\right)-\sin\left( \beta\right)\right) \right)\\ &&*\left( \sin\left( \alpha-\beta\right)+\left( \sin\left( \alpha\right)-\sin\left( \beta\right)\right)\right)...-8\left( 1-\cos\left( \alpha-\beta\right)\right), \end{array} $$
(34)

where the derivative, which is required for Newton’s method, is given by

$$\begin{array}{@{}rcl@{}} f^{\prime}\left( a\right)&=&\frac{\partial f}{\partial a}=\left( \left( 6N\pi+3\xi-\eta\right)\left( \cos\left( \xi\right)+\cos\left( \alpha\right)\right)\right....\\ &&\left.+\left( 3-\cos\left( \alpha\right)\right)\left( \sin\left( \xi\right)+\eta\right)-8\sin\left( \xi\right)\right) \left( -\frac{1}{a}\tan\left( \frac{\alpha}{2}\right)\right)...\\ &&+\left( \left( 6N\pi+3\xi-\eta\right)\left( -\cos\left( \xi\right)-\cos\left( \alpha\right)\right)\right....\\ &&+\left.\left( -3-\cos\left( \beta\right)\right)\left( \sin\left( \xi\right)+\eta\right)+8\sin\left( \xi\right)\right) \left( -\frac{1}{a}\tan\left( \frac{\beta}{2}\right)\right), \end{array} $$
(35)

and ξ ≡ α − β and η = sin (α) − sin (β). A good initial guess is a = 1.001a m since the converged value will be bigger than a m . Once the value of a is found for a particular N > 0, \(t_{min_{N}}\) can be computed using Eq. 32. If t d e s is less than say t m i n3, then N m a x = 2 and there are 5 solutions which must be found. If \(t_{des}=t_{min_{N_{max}}}\) then the two solutions on the N m a x branch are equal and there are a total of 2N m a x unique solutions.

Once the number of solutions is determined, another Newton iteration is require for determining the values of these solutions which are the a’s that correspond to the specified t d e s . That is, Eq. 36 must be satisfied iteratively, where Δt is the current transfer time estimate on a particular iteration.

$$ g(a)=t_{des}(a)-{\Delta} t=0. $$
(36)

The derivative, which is also required for Newton’s method, is given by

$$ \frac{\partial{\Delta} t}{\partial a}=\frac{\frac{1}{2}\left( \frac{a}{\mu}\right)^{\frac{1}{2}}}{\sin\left( \alpha- \beta\right)+\left( \sin\left( \alpha\right)-\sin\left( \beta\right)\right)}f\left( a\right), $$
(37)

where the values of α and β are computed using Eqs. 23 and 24 respectively. If \({\Delta } t\leq t_{m_{N}}\) then α = α 0 is used and the solution falls on the lower branch; if \({\Delta } t>t_{m_{N}}\) then α = 2π − α 0 and the solution falls on the upper branch. If \(t_{min_{N_{max}}}\leq {\Delta } t\leq t_{m_{N_{max}}}\), that is the time of flight on the current iteration is greater than the minimum possible time in which to make the transfer, but smaller than the time of flight corresponding to the minimum energy transfer ellipse, then the situation is a little more challenging as both solutions fall on the lower branch of the curve and thus α = α 0 for both solutions. In this case the solutions lie on opposite sides of a t m i n , the semimajor axis associated with the minimum possible transfer time, and this information can be used to pick an appropriate initial guess for a.

Terminal Velocity Vectors

Once the value of a is known the terminal velocity vectors can be computed. These may be written as a set of skewed unit vectors that are co-linear to the local radius and the chord respectively.

$$ \textit{\textbf{u}}_{1}\equiv\frac{\textit{\textbf{r}}_{1}}{r_{1}}, $$
(38)
$$ \textit{\textbf{u}}_{2}\equiv\frac{\textit{\textbf{r}}_{2}}{r_{2}}. $$
(39)
$$ \textit{\textbf{u}}_{c}\equiv\frac{\left( \textit{\textbf{r}}_{2}-\textit{\textbf{r}}_{1}\right)}{c}. $$
(40)

Prussing and Conway [20] states that the initial velocity vector (v 1) can be expressed as

$$ \textit{\textbf{v}}_{1}=\left( B+A\right)\textit{\textbf{u}}_{c}+\left( B-A\right)\textit{\textbf{u}}_{1} $$
(41)

where

$$ A=\left( \frac{\mu}{4a}\right)^{1/2}\cot\left( \frac{\alpha}{2}\right), $$
(42)
$$ B=\left( \frac{\mu}{4a}\right)^{1/2}\cot\left( \frac{\beta}{2}\right), $$
(43)

and the values of α and β are determined from Eqs. 23 and 24 respectively. The final velocity vector (v 2) is computed as follows:

$$ \textit{\textbf{v}}_{2}=\left( B+A\right)\textit{\textbf{u}}_{c}-\left( B-A\right)\textit{\textbf{u}}_{2}. $$
(44)

Knowing the value for the initial and final velocity on the transfer orbit allows a Δv value for the specific transfer to be computed.

It is important to note that in general, not all the possible solutions are feasible. Some will collide with the Earth (green and cyan in Fig. 4), some exceed escape velocity, and others, near π and multiples of π, are undefined as a result of the plane ambiguity that is associated with a 180° transfer in Lambert’s problem. In addition, if the transfer orbit Δv exceeds an upper limit imposed by the mission then the simulated solution must also be treated as infeasible.

Algorithm Efficiency: MPS vs Newton-shooting

To compare the computational efficiency of MCPI-MPS to the Newton-shooting method, where RK(12)10 is used as the integrator, we perform four example orbit transfers spanning low Earth orbit (LEO), medium Earth orbit (MEO), geostationary transfer orbit (GTO), and Molniya or high Earth orbit (HEO). For each test case a two-body initial guess is used to start the computation of the perturbed orbit transfer that considers a (40 × 40) degree and order EGM2008 gravity model.

Figures 6, 7, 8 and 9 show the computation time in milliseconds (top panel) and the accuracy to which the final boundary conditions are met (bottom panel). These computations were performed in serial on the head node of the LASR Lab SSA computer cluster. Each of the compute nodes has a pair of Intel Xeon 2.6GHz CPU and 64GB of RAM. In all cases the integrators are tuned such that the transfer trajectories preserve the Hamiltonian to machine precision. The Newton-shooting method makes use of a state transition matrix that is populated with the two-body partials. We found that including partials for the full spherical harmonic gravity approximation significantly increased the computation time while providing negligible improvement in the accuracy.

Fig. 6
figure 6

Accuracy and efficiency comparison for varying time-of-flight transfers along a LEO using MCPI-MPS and Newton-RK(12)10-shooting

Full size image
Fig. 7
figure 7

Accuracy and efficiency comparison for varying time-of-flight transfers along a MEO using MCPI-MPS and Newton-RK(12)10-shooting

Full size image
Fig. 8
figure 8

Accuracy and efficiency comparison for varying time-of-flight transfers along a GTO using MCPI-MPS and Newton-RK(12)10-shooting

Full size image
Fig. 9
figure 9

Accuracy and efficiency comparison for varying time-of-flight transfers along a HEO using MCPI-MPS and Newton-RK(12)10-shooting

Full size image

Each plot consists of an average over several runs: 10 runs with an inclination of 0°, 10 runs with an inclination of 10°, and 10 runs with an inclination of 30°. This allows more of the gravity field to be sampled and results in a more representative comparison of the methods. In all four test cases our MCPI-MPS algorithm outperforms the Newton-RK(12)10-shooting method with regard to efficiency, while we obtain essentially the same (less than half an order of magnitude) or better accuracy.

Conclusion

We presented a new method for solving the multiple revolution perturbed Lambert problem using the method of particular solutions and modified Chebyshev-Picard iteration. Any numerical integrator could be used for solving two-point boundary problems with the method of particular solutions; however, we showed that using modified Chebyshev-Picard iteration afforded an avenue for increased efficiency that was not available with other step-by-step integrators. We utilized a variable fidelity force model for propagating the reference trajectory and demonstrated that computing the particular solutions with only low fidelity function evaluations resulted in our algorithm being about an order of magnitude faster compared with the classical shooting method and a tenth-twelfth order Runge-Kutta integrator. It is well known that the solution to Lambert’s problem over multiple revolutions is not unique and to ensure that all possible solutions are considered we made use of a reliable preexisting Keplerian Lambert solver to warm start our perturbed algorithm.