FormalPara Key Points for Decision Makers

Validation of economic model accuracy is essential to ensure confidence in the outcomes generated.

We applied best practice guidelines to perform external validation of how accurately the Core Obesity Model (COM) predicted rates of obesity-related complications, including cardiovascular disease, type 2 diabetes, obstructive sleep apnoea and mortality.

The COM predictions show good concordance with the results of studies used to develop the model and those not included in the model, suggesting that the model is suitable for decision-making.

1 Introduction

Obesity, defined as a body mass index (BMI) of 30 kg/m2 or greater, affects more than 650 million people worldwide [1], and is increasing in prevalence. The clinical, economic and humanistic impact of obesity is considerable, in large part due to the multifactorial aetiology and chronic nature of complications. Known complications linked to obesity comprise obstructive sleep apnoea (OSA) [2], type 2 diabetes (T2D), hypertension, dyslipidaemia and cardiovascular disease (CVD), including stroke, myocardial infarction (MI) and coronary heart disease [3, 4]; consequently, obesity is associated with severe long-term morbidity and increased mortality. The impact of obesity on health-related quality of life (HRQoL) is also well documented. It is well established that obesity has a psychological impact as a result of social stigmatization, exclusion and isolation [5]; this finding is supported by data indicating that obesity is associated with significantly reduced scores for both the physical and mental components of the 36-item Short-Form Health Survey (SF-36) [6].

Obesity is associated with high direct costs to healthcare systems [7], a large proportion of which arise from treating comorbidities [8], as well as substantial indirect costs to society [9]. Given the high prevalence of obesity and its comorbidities, the development of economic models is vital for providing long-term estimates of its clinical effects and economic impact, allowing comparison of weight management interventions and informing healthcare decisions about allocation of scarce resources. The evidence used for these decisions is often taken from clinical trials, which typically assess outcomes over short-term follow-up periods; however, in many cases, certain treatment benefits may be detected only several years, or even decades, after initiation of therapy [10]. Therefore, the use of economic models based on short-term clinical data to project long-term outcomes is widely used to aid decision-making [11].

The usefulness of an economic model depends on it being fit for purpose; furthermore, it is vital that its outputs can be interpreted with confidence by clinicians, budget holders and other stakeholders. This need for accuracy and transparency in model development has led to the development of best practice guidelines by, for example, the International Society for Pharmacoeconomics and Outcomes Research (ISPOR) and the Society for Medical Decision Making (SMDM) [12, 13]. For T2D, validation of existing health economic models has been carried out widely and according to best-practice guidance, with collaboration between study groups to assess and compare different models [14, 15]. In contrast, although some obesity models have been the subject of validation studies, formal validation has not been attempted for a large proportion of published models. In a systematic review of obesity models, only 14% (10/72) of the identified model-based health economic assessments included a published external validation, highlighting a general lack of such validations [16].

The Core Obesity Model (COM) is a Markov, closed-cohort model consisting of health states that represent the most common complications associated with obesity (Fig. 1) [17]. The inputs can be adjusted to model populations with normal weight, overweight or obesity, allowing comparison of outcome risks for different weight profiles. The outcomes included in the model are considered to have either strong evidence (T2D, acute coronary syndrome [ACS], stroke and sleep apnoea) or moderate evidence (knee replacement, postmenopausal endometrial cancer, postmenopausal breast cancer and colorectal cancer) for their association with obesity, based on a comprehensive report from the World Health Organization [18]. Furthermore, these outcomes are affected by weight loss, and can have substantial consequences for healthcare resource use and costs, patients’ quality of life and/or life expectancy. The COM also allows inclusion of healthcare payer, patient and societal costs, permitting cost-effectiveness analyses encompassing the broad impact of obesity.

Fig. 1
figure 1

Structure of the Core Obesity Model. ACS acute coronary syndrome, BMI body mass index, HbA1c glycated haemoglobin, SBP systolic blood pressure, T2D type 2 diabetes

Full size image

State-transition models have previously been used to model obesity [19,20,21] and diabetes [22], indicating that this approach is well suited to modelling a condition characterized by recurrent risks. Furthermore, by using a cohort state-transition model, we aimed to maximize transparency and user-friendliness while minimizing run-times and avoiding some common disadvantages of micro-simulation models relating to extensive model code and computational intensiveness [23].

The major focus of this study is external validation to determine how accurately the COM predicts outcomes strongly associated with obesity, including CVD (defined as ACS and stroke; heart failure and peripheral artery disease are not included among COM outcomes), T2D, obstructive sleep apnoea and mortality (cardiovascular [CV] and all-cause).

2 Objectives

In this study, we report the validation of the COM (version 6.1) in line with published guidance [13], with a focus on external validation of the model by comparison with results of published epidemiological and clinical studies, thus assessing whether the model is robust and fit for purpose.

3 Methods

The best practice guidelines from ISPOR/SMDM recommend five forms of validation: face validity, verification, cross validation, external validation and predictive validation [13]. The major focus of this study is on the results observed during the external (dependent and independent) validations.

3.1 External Dependent and Independent Validation Process

The external validations were based on a three-step process encompassing the identification of suitable sources and outcomes, populating the COM with relevant inputs to predict study outcomes, and the assessment of concordance between predicted and observed outcomes.

3.1.1 Identification of Relevant Studies

The studies used to provide inputs during the development of the COM were used for dependent validation (Online Resource 1, see the electronic supplementary material). For independent validation, a systematic review [16] was consulted to identify relevant studies in normoglycaemic or prediabetic populations, whereas relevant studies for populations with T2D were sourced from the published validation of the Economic and Health Outcomes Model of Type 2 Diabetes Mellitus (ECHO-T2DM) model [10]. In a subsequent step, targeted searches were conducted via Medline and Google to identify additional studies. This version of the COM (6.1) was designed to assess the long-term cost-effectiveness of weight management interventions for the primary prevention of CVD and other obesity-related complications; consequently, studies in primary prevention (i.e. those with CVD history as an exclusion criterion, or those in which the proportion of individuals with CVD was less than 15%) were selected for validation (Online Resource 2). Furthermore, several criteria were used to select studies that were relevant for inclusion in the independent validation. Firstly, they were considered to have potential for replication because data on baseline characteristics and long-term trends of risk factor progression were publicly available. Furthermore, selected studies had a sufficiently long time horizon, included individuals who were overweight or obese, and reported endpoints that were identical or similar to those included in the COM.

The external independent validation of CV outcomes and mortality in normoglycaemic or prediabetic populations was performed using data from five randomized controlled trials (RCTs) [24,25,26,27,28] and four observational studies [29,30,31,32] identified in the systematic review. A further five studies allowed validation of these outcomes in populations with T2D [33,34,35,36,37]. Four studies from the review were selected for the validation of T2D incidence [25, 27, 38, 39], and six studies for the validation of OSA, which reported data pairs of OSA prevalence and underlying BMI levels across 21 populations [40,41,42,43,44,45]. In line with recommendations from ISPOR/SMDM, data sources that provided sufficient details (e.g. patient characteristics at baseline) to enable replication of design and progression of the study or data source were prioritized for inclusion in the validation [13].

3.1.2 Inclusion of Relevant Endpoints

Endpoints from relevant studies were included in the analysis only if their definitions were the same as, or similar to, those used in the COM, so that substantial mismatches could be ruled out. For studies that reported composite endpoints of interest, the feasibility was assessed of estimating the composite endpoints by adding individual endpoint components of the COM. Endpoint definitions for CVD and mortality outcomes from studies included in the independent validation and the approach taken to match these endpoints in the COM are provided in Online Resource 3.

The following clinical events were assessed to determine external validity: onset of T2D, OSA, fatal or non-fatal MI, fatal or non-fatal unstable angina, fatal or non-fatal stroke, CV mortality (a composite of fatal MI, fatal angina and fatal stroke) and all-cause mortality. For the purposes of presenting results, these events were subsequently grouped into three categories: CVD and mortality, T2D incidence, and OSA.

3.1.3 Populating the Core Obesity Model

For each dependent or independent validation exercise, the model was populated with the baseline clinical and demographic characteristics of the populations included in the relevant study. The inputs and assumptions applied as part of the dependent CVD and mortality validations are presented in Online Resource 4 (see the electronic supplementary material); those used for the independent validations are presented in Online Resource 5, 6 and 7.

Treatment effects and the progression of risk factors over time were replicated in the model whenever such data were reported. When risk factor progression was not published in dependent validation studies, BMI was assumed to increase by 0.1447 kg/m2/year in men and 0.1747 kg/m2/year in women [19]. A linear increase of 0.5 mmHg/year was assumed for systolic blood pressure (SBP) in all individuals [46], but no changes in total cholesterol [47] or high-density lipoprotein cholesterol were included. In the independent validation, no progression of these risk factors was assumed. For all validations, glycated haemoglobin (HbA1c) was varied based on a published natural-progression approach [48].

The modelled time horizon was defined to match the mean or median follow-up duration of each study, and the model was applied at a cohort size of 100 patients. For cases in which the COM (which is based on annual cycle length) was compared with studies in which follow-up duration was not an integer value, the model was applied to the upper and lower integer years and linear interpolation was used to ensure that the time frame of the prediction matched the study follow-up.

Throughout all validation exercises the default configurations of risk equations in the COM were applied, from the following sources:

T2D incidence: QDiabetes® [49]

Primary CV events in normoglycaemic and prediabetic populations: QRISK®3 [50]

Secondary CV events in normoglycaemic populations: Framingham [51]

Primary and secondary CV events in T2D populations: UK Prospective Diabetes Study (UKPDS) 82 [52]

3.1.4 Assessment of Concordance

Several statistical tests have been proposed for comparing model predictions with observed outcomes; however, there is no consensus on the best approach [10]. Model concordance was evaluated by assessing goodness of fit. Visual inspection of model fit was undertaken by plotting the predicted outcomes (y axis) against the observed study endpoints (x axis). A 45° identity line (IL) was then plotted, reflecting a situation whereby the predicted and observed results matched perfectly. Overpredictions or underpredictions were indicated by large numbers of points above or below the IL, respectively. Additionally, an ordinary least-squares linear regression line (OLS LRL) was fitted to the data. This had an intercept of zero to attribute more weight to the OLS LRL slope. A value for the slope markedly lower than 1.0 suggests underprediction by the model and a slope value greater than 1.0 suggests overprediction. Coefficient of determination (R2) was obtained for all validation results and quantifies how close the validation outcomes were to the OLS LRL.

A number of mean error estimates were generated as part of the validations, to provide a broad picture of areas in which model fit was poor and to quantify the magnitude of mismatch between the predicted and observed data. The estimates generated were mean absolute percentage error (MAPE), root mean squared percentage error (RMSPE), mean squared log of accuracy ratio (MSLAR) and mean squared root logit error (MSLE). If the model predicted outcomes perfectly, the measures of error would equal zero. The quality of the prediction decreased with increasing values.

4 Results

Full details of the outcomes from the dependent and independent validations are provided in Online Resource 8 (dependent) and Online Resource 9, 10, 11, 12 and 13 (independent) (see the electronic supplementary material); key results are discussed below.

4.1 Dependent Validation

4.1.1 CVD

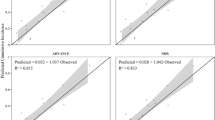
External dependent validations for CVD were conducted against the Framingham Heart Study, QRISK®3 and the UKPDS 80 [50, 53, 54]. Overall, there was concordance between the outcomes predicted by the COM and the outcomes observed in the three studies (Fig. 2a; relationship between predicted and observed outcomes in each study displayed as separate data points). The results displayed a high degree of linear correlation (R2 = 0.927), and only a modest underestimation of validation outcomes (indicated by the slope of the OLS LRL = 0.859).

Fig. 2
figure 2

Observed versus predicted results from the dependent validations of a CVD and mortality outcomes, b T2D incidence and c OSA prevalence. a Linear regression analysis of observed versus predicted CVD and mortality outcomes (symbols), with the solid line representing the IL and the dashed line representing the OLS LRL and associated 95% confidence interval (grey area) [50, 53, 54]. b Linear regression analysis of observed versus predicted T2D incidence outcomes (symbols), with the solid line representing the IL and the dashed line representing the OLS LRL [49, 55]. c Observed OSA prevalence with increasing BMI as given in the SHHS [56]. BMI body mass index, CV cardiovascular, CVD cardiovascular disease, IL identity line, MI myocardial infarction, OLS LRL ordinary least-squares linear regression line, OSA, obstructive sleep apnoea, R2 coefficient of determination, SHHS Sleep Heart Health Study, T2D type 2 diabetes, TIA transient ischaemic attack

Full size image

4.1.2 T2D

External dependent validation of T2D incidence was conducted using the Framingham Offspring Study and QDiabetes® [49, 55]. Overall, there was almost 100% concordance between the observed and predicted outcomes for T2D incidence. The corresponding slope of the OLS LRL was 0.942, and the R2 statistic was 0.979 (Fig. 2b).

4.1.3 OSA

The COM uses data from the Sleep Heart Health Study [56] to predict OSA prevalence conditional on time-updated BMI; therefore, external dependent validation for OSA involved verification of consistency between the associations derived from this study and related changes in OSA prevalence following BMI variations in the COM. External dependent validation found 100% concordance between these associations, resulting in a single line when plotted (Fig. 2c).

4.1.4 Mean Error Estimates

A summary of the mean error rate outcomes observed from the external validations of the COM is presented in Table 1. Overall, the mean error rates were lowest in predictions of T2D incidence, with MAPE, RMSPE, MSLAR and MSLE values of 10.6%, 12.3%, 1.5% and 0.0%, respectively, compared with values of 25.4%, 32.9%. 10.7% and 3.9%, respectively, for predictions of CVD and mortality events.

Table 1 Summary of external validation mean error values
Full size table

4.2 Independent Validation

4.2.1 CVD

External independent validations were conducted for CVD and mortality using 14 studies, which encompassed more than 150 outcomes [24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Overall, the incidence of study outcomes tended to be slightly underestimated by the COM, especially for CV mortality outcomes. The slope of the OLS LRL was estimated at 0.811, accompanied by a linear correlation coefficient of R2 = 0.819 (Fig. 3a).

Fig. 3
figure 3

Observed versus predicted results from the independent validations of a CVD and mortality outcomes, b T2D incidence and c OSA prevalence. a Linear regression analyses of observed versus predicted CVD and mortality outcomes (symbols), with the solid line representing the IL and the dashed line representing the OLS LRL and associated 95% confidence interval (grey area) [24,25,26,27,28,29,30,31,32,33,34,35,36,37]. b Linear regression analysis of observed versus predicted T2D incidence (symbols), with the solid line representing the IL and the dashed line representing the OLS LRL and associated 95% confidence interval (grey area) [25, 27, 38, 39]. c Observed OSA prevalence with increasing BMI as given in the SHHS (solid line) compared with observed outcomes stratified by BMI group (symbols) [40,41,42,43,44,45]. ACM all-cause mortality, BMI body mass index, CV cardiovascular, CVD cardiovascular disease, IL identity line, MI myocardial infarction, OLS LRL ordinary least-squares linear regression line, OSA obstructive sleep apnoea, R2 coefficient of determination, SHHS Sleep Heart Health Study, T2D type 2 diabetes

Full size image

Scenario analyses encompassing stratification of the overall results for CVD and mortality events by specific populations (populations with normal glucose tolerance, prediabetes or T2D), by study design (RCT or observational study) and by individual CVD outcomes (MI, stroke, unstable angina and mortality) are presented in Online Resources 11, 12 and 13 (see the electronic supplementary material). The analyses suggest that the observed underprediction in the overall results may be a result of predictions made specifically in populations with T2D (Online Resource 14a), comparisons with results from RCTs (Online Resource 15a) and predictions of stroke or mortality (including all-cause mortality and CV mortality) events (Online Resource 16b and d). There was also a moderate overestimation of angina events by the model (Online Resource 16c).

4.2.2 T2D

External independent validations for T2D incidence were conducted using four studies [25, 27, 38, 39]. Overall, the incidence of T2D in these studies tended to be slightly underestimated by the COM (Online Resource 12). As such, the slope of the OLS LRL was estimated at 0.838, and a high degree of linear correlation was observed (R2 = 0.968; Fig. 3b).

4.2.3 OSA

External independent validation was based on the comparison of reported OSA prevalence score and underlying BMI levels across six studies [40,41,42,43,44,45] (Online Resource 13). The distribution of study estimates was wide but homogeneous, suggesting that the values presented in the Sleep Heart Health Study [56] provide a reasonable average of the observed data (Fig. 3c). Due to the shape of the relationship, the OLS LRL and R2 statistics have limited value.

4.2.4 Mean Error Estimates

A summary of the mean error rate outcomes observed from the dependent validations of the COM is presented in Table 1. Overall, the mean error estimates generated during the independent validations were higher than those observed for the dependent validations. Furthermore, the mean error estimates were generally lowest for the predictions of CVD and mortality events, with MAPE, RMSPE, MSLAR and MSLE values of 55.2%, 93.0%, 31.2% and 20.0%, respectively.

5 Discussion

The ISPOR/SMDM guidelines highlight the need for transparency and validation to ensure that economic models are fit for purpose and that their outputs can be interpreted with confidence [13]; however, the majority of published economic models in obesity have not been subject to external validation [16]. In this study, we focussed on the results of the external dependent and independent validations of the COM, which build on the face validity and verification that had been conducted throughout model development. Face validity was evaluated using clinical expert feedback and discussions arising from presentation of the model structure at conferences. Verification was performed through reproduction of computational examples of the published risk equations or via consistency checks with a double-programming approach, which demonstrated a 100% correspondence between distinct model implementations, thereby confirming an error-free use of risk equations within the COM. The use of prospective validation was not feasible at the time of this analysis; a cross-validation analysis is planned as a future publication.

Having performed both dependent and independent external validation, our findings suggested that the risk equations upon which the COM is based generate reasonable predictions, and the model is likely to be generalizable to other settings, including different countries and patient populations. The concordance between model predictions and the selected studies also suggests that, based on mean results, the COM predicts event rates with reasonable accuracy.

Independent validations of the COM showed good concordance with the results of relevant studies, as indicated by high coefficients of determination; however, there was a degree of underprediction for CVD and mortality outcomes, and for T2D incidence. Scenario analyses revealed that this overall underprediction of CV events by the COM may stem from predictions made in populations with T2D, comparisons made with outcomes from RCTs or predictions of stroke and mortality. Furthermore, the underprediction observed for all-cause mortality demonstrates the continuing refinement required for economic models, and highlights the incomplete understanding of the relationship between BMI and mortality. The finding that CV death was also underestimated suggests that there may be unknown risk factors that result in the underestimation of mortality in individuals with obesity. Furthermore, the underprediction observed during comparisons with the results from RCTs may have been due to the specific baseline characteristics of the study populations included in these trials. Indeed, many of the study populations did not include individuals with obesity, and some also included study populations with restricted lipid profiles [27].

The underprediction observed may have also resulted from the use of mean inputs into the COM, which are not fully representative of the heterogeneous populations in the real world [57]. However, it should be noted that alternative, probabilistic modelling approaches that assume sampling with distributions typically tend to predict higher event rates than use of mean inputs. Furthermore, the underprediction of CVD outcomes in both the dependent and independent validations may have occurred because of the absence of CVD at baseline in the COM, whereas individuals with CVD at baseline were included in some of the comparator studies, comprising up to 15% of the population. It should be noted that some of the observed underpredictions may be mitigated when using the COM to generate incremental outcomes, because the underprediction would be present in both the intervention and comparator arms provided that it is independent of treatment effects. However, the underprediction of some CVD outcomes may extend to events that would be prevented by treatment, resulting in treatment efficacy being underestimated and thus leading to higher incremental cost-effectiveness ratios than those generated by a model that does not show the same tendency for underprediction.

These analyses were performed in accordance with best-practice recommendations for the validation of cost-effectiveness models [12, 13], and the concordance between external validations adds weight to our conclusions. The findings were based on several different observations encompassing goodness of fit, in addition to visual inspection, R2 statistics, match between the IL and the OLS LRL, and error terms. Furthermore, the independent external validation was performed across a broad range of studies, spanning 193 validation endpoints (162 CV and mortality outcomes, ten T2D incidence outcomes and 21 OSA outcomes). These studies also comprised a mixture of RCTs and observational studies conducted across different countries and across different time periods, improving confidence that the concordance observed is generalizable across multiple settings. Although the concordance of these observations is improved by inclusion of numerous studies and endpoints, it should also be noted that the disparities between the populations included in RCTs and those in observational studies may have contributed to some of the overestimation and underestimation by the model.

Given the nature of validation analyses, there were some limitations to our study. Some of the baseline characteristics required to populate the COM (SBP, total cholesterol, high-density lipoprotein cholesterol, proportion of individuals who smoke) and measures of risk factor evolution over time (e.g. natural increase in weight) were not available for all comparator studies, and use of substitute values may have introduced some uncertainty by creating mismatches between the simulated cohort and the study participants. This risk was mitigated by carefully selecting the studies used to populate these missing values, ensuring that they had a similar population to the other studies included in the validation. These mismatches between simulated and study populations may have been particularly apparent in comparisons with RCTs because of their more stringent inclusion criteria and follow-up periods, compared with those of observational studies. Indeed, the scenario analysis in which CVD outcomes were stratified by study design showed a larger underprediction for comparisons with RCTs than with observational studies, suggesting that the predictions may have been closer to observed values if RCTs were omitted from the independent validation. A further limitation that is common to economic models is the fact that the accuracy of predictions depends on the quality and scope of the data available at the time of development. A key area of future development will be the identification of additional correction factors, to mitigate the possibility that known and/or unknown factors underlie the observed underprediction of mortality. Additionally, our model was affected by a lack of available risk equations that encompass changes in BMI as a covariate, which meant that we could not fully assess residual risk of BMI history.

Our results indicate the accuracy of predictions made using a cohort state-transition model of obesity; a comparison of the accuracy of different modelling methods in this disease area would be of value in the future, but falls outside the scope of this analysis. We also focused on external validation of event risk predictions made by the COM rather than comparisons of observed and predicted costs. Such analyses are complex to conduct [13], and would require a separate publication to explore fully.

6 Conclusion

These external validation analyses revealed that the predictions generated by the risk equations used in the COM show good concordance both with the studies used to develop the model and with other studies not included in the model. Despite this concordance, the predictions made by the COM can be improved; the ability of this model to capture the impact of existing CV risk, as well as mortality, are key areas for future refinement. Taken together, these results should increase confidence in the estimates derived from the COM and reduce uncertainty associated with analyses using this model.