Skip to main content
SpringerLink
Log in

Fatigue experiments and finite element analysis of bolted/bonded double lap joints

  • Research Paper
  • Published:
Welding in the World Aims and scope Submit manuscript

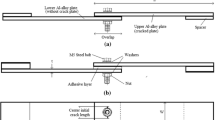
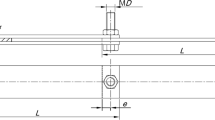
Abstracts

High-strength steel hybrid joints that combine adhesive and bolts have been studied both experimentally and numerically. The fatigue strength of the double lap joint has been experimentally measured under completely reversed cyclic loading. Finite element analysis was used to estimate the stress state at the contact interface of the lap joint. The fatigue strength of bonded and clamped interfaces which have previously been characterized using napkin ring specimens has been combined with the finite element results. The region of the double lap joint which showed fretting damage corresponded well with the region estimated to have significant damage based on the assessment. The resulting fatigue strength assessment was conservative with respect to the experimental results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

d :

Loading level interval between subsequent fatigue tests in the small sample staircase series

D :

Damage variable of the cohesive interface model

E :

Young’s modulus

F :

Longitudinal load applied to the double lap joint specimen

\( {\mathit{\mathsf{F}}}_{\mathsf{a}} \) :

Load amplitude applied during the double lap joint experiment

\( {\mathit{\mathsf{F}}}_{\mathsf{a},0} \) :

First load amplitude level of the staircase sequence

\( {\mathit{\mathsf{F}}}_{\mathsf{a},\mathsf{f}} \) :

Load amplitude corresponding to the estimated fatigue strength

\( {\mathit{\mathsf{G}}}_{\mathit{\mathsf{c}}} \) :

Fracture energy

k :

Parameter based on the staircase sequence

\( {\mathit{\mathsf{K}}}_{\mathsf{nn}},{\mathit{\mathsf{K}}}_{\mathsf{ss}},{\mathit{\mathsf{K}}}_{\mathsf{tt}} \) :

Cohesive stiffness component in the normal and in the two shear directions, respectively

\( {\mathit{\mathsf{N}}}_{\mathsf{f}} \) :

Number of cycles to failure

P :

Longitudinal load applied to the double lap joint finite element model as surface pressure

\( {\mathit{\mathsf{P}}}_{\max } \) :

Maximum load during the double lap joint simulation

\( {\mathit{\mathsf{P}}}_{\min } \) :

Minimum load during the double lap joint simulation, maximum compressive load

q :

Static normal stress on the interface of the modified napkin ring specimen

\( {\mathit{\mathsf{t}}}_{\mathsf{n}},{\mathit{\mathsf{t}}}_{\mathsf{s}},{\mathit{\mathsf{t}}}_{\mathsf{t}} \) :

Cohesive traction in the normal and in the two shear directions, respectively

\( {\overline{\mathit{\mathsf{t}}}}_{\mathsf{n}},{\overline{\mathit{\mathsf{t}}}}_{\mathsf{s}},{\overline{\mathit{\mathsf{t}}}}_{\mathsf{t}} \) :

Elastic traction without damage in the normal and in the two shear directions, respectively

\( {\mathit{\mathsf{t}}}_{\mathsf{n}}^0,{\mathit{\mathsf{t}}}_{\mathsf{s}}^0,{\mathit{\mathsf{t}}}_{\mathsf{t}}^0 \) :

Critical cohesive traction in the normal and in the two shear directions, respectively

α :

Coefficient of the exponential damage evolution model

Δ :

Interface relative displacement during a modified napkin ring experiment

\( {\varDelta}_{\mathsf{gap}} \) :

Displacement measured by the clip-on gage during the double lap joint test

\( {\varDelta}_{\mathsf{tot}} \) :

Total displacement measured by the built-in sensor during the double lap joint test

\( {\delta}_{\mathsf{n}},{\delta}_{\mathsf{s}},{\delta}_{\mathsf{t}} \) :

Cohesive relative displacement in the normal and in the two shear directions, respectively

\( {\delta}_{\mathit{\mathsf{m}}} \) :

Effective separation

\( {\delta}_{\mathit{\mathsf{m}}}^0 \) :

Effective separation at onset of damage

\( {\delta}_{\mathit{\mathsf{m}}}^{\mathsf{f}} \) :

Effective separation at full cohesive fracture

\( {\delta}_{\mathit{\mathsf{m}}}^{\max } \) :

Maximum effective separation attained during the loading history

μ :

Coefficient of friction

ν :

Poisson’s ratio

σ 2 :

Calculated contact pressure on the interface

τ 1 :

Calculated interface shear stress along the global 1-direction

\( {\tau}_{\mathit{\mathsf{II}}} \) :

Measured shear stress during a modified napkin ring experiment

\( {\tau}_{\mathsf{f}} \) :

Shear stress amplitude corresponding to the estimated fatigue strength of the bonded and clamped interfaces

CZM:

Cohesive zone modelling

DLJ:

Double lap joint

FEM:

Finite element method

HSS:

High-strength steel

References

  1. Hurme S, Marquis G (2013) The effect of clamping stress on the fatigue strength of bonded high-strength steel interfaces. Weld World 57:285–292

    Google Scholar 

  2. Oinonen A, Marquis G (2011) A parametric shear damage evolution model for combined clamped and adhesively bonded interfaces. Eng Fract Mech 78:163–174

    Article  Google Scholar 

  3. Hurme S, Oinonen A, Marquis G (2011) Fatigue of bonded steel interfaces under cyclic shear loading and static normal stress. Eng Fract Mech 78:1644–1656

    Article  Google Scholar 

  4. Oinonen A, Marquis G (2011) Shear decohesion of clamped abraded steel interfaces reinforced with epoxy adhesive. Int J Adhes Adhes 31:550–558

    Article  Google Scholar 

  5. Dixon WJ, Mood AM (1948) A method for obtaining and analyzing sensitivity data. J Am Stat Assoc 43:109–126

    Article  Google Scholar 

  6. Dixon WJ (1965) The up-and-down method for small samples. J Am Stat Assoc 60:967–978

    Article  Google Scholar 

  7. Little RE (1974) The up-and-down method for small samples with extreme value response distributions. J Am Stat Assoc 69:803–806

    Article  Google Scholar 

  8. Nowell D, Dini D, Hills DA (2006) Recent developments in the understanding of fretting fatigue. Eng Fract Mech 73:207–222

    Article  Google Scholar 

  9. Ciavarella M, Demelio G (2001) A review of analytical aspects of fretting fatigue, with extension to damage parameters, and application to dovetail joints. Int J Solids Struct 38:1791–1811

    Article  Google Scholar 

  10. Nesládek M, Španiel M, Jurenka J, Růžička J, Kuželka J (2012) Fretting fatigue—experimental and numerical approaches. Int J Fatigue 44:61–73

    Article  Google Scholar 

  11. Benhamena A, Talha A, Benseddiq N, Amrouche A, Mesmacque G, Benguediab M (2010) Effect of clamping force on fretting fatigue behaviour of bolted assemblies: case of couple steel–aluminium. Mater Sci Eng A 527:6413–6421

    Article  Google Scholar 

  12. Chakherlou TN, Razavi MJ, Abazadeh B (2013) Finite element investigations of bolt clamping force and friction coefficient effect on the fatigue behaviour of aluminium alloy 2024-T3 in double shear lap joint. Eng Fail Anal 29:62–74

    Article  Google Scholar 

  13. Wagle S, Kato H (2009) Ultrasonic detection of fretting fatigue damage at bolt joints of aluminium alloy plates. Int J Fatigue 31:1378–1385

    Article  Google Scholar 

  14. Volkersen O (1938) The rivet load distribution in tensile loaded riveted joints with constant lap cross sections (Die Nietkraftverteilung in zugbeanspruchten Nietverbindungen mit konstanten Laschenquerschnitten). Luftfahrtforschung 15:41–47

    Google Scholar 

  15. Kwakernaak A, Hofstede J, Poulis J, Benedictus R (2010) Improvements in bonding metals (steel, aluminium). In: Dillard DA (ed) Advances in structural adhesive bonding. Woodhead Publishing Limited, Cambridge, pp 185–236

    Chapter  Google Scholar 

  16. De Bruyne NA (1944) The strength of glued joints. Aircr Eng 16:115–118

    Article  Google Scholar 

  17. Tsai MY, Oplinger DW, Morton J (1998) Improved theoretical solutions for adhesive lap joints. Int J Solids Struct 35:1163–1185

    Article  Google Scholar 

  18. Osnes H, McGeorge D (2009) Experimental and analytical strength analysis of double lap joints for marine applications. Compos B 40:29–40

    Article  Google Scholar 

  19. Gonçalves JPM, De Moura MFSF, de Castro PMST (2002) A three-dimensional finite element model for stress analysis of adhesive joints. Int J Adhes Adhes 22:357–365

    Article  Google Scholar 

  20. Griffith AA (1921) The phenomena of rupture and flow in solids. Philos Trans R Soc A221:163–198

    Article  Google Scholar 

  21. Castagnetti D, Dragoni E, Spaggiari A (2011) Failure analysis of complex bonded structures: experimental tests and efficient finite element modeling by tied mesh method. Int J Adhes Adhes 31:338–346

    Article  Google Scholar 

  22. De Moura MFSF, Gonçalves JPM, Chousal JAG, Campilho RDSG (2008) Cohesive and continuum mixed-mode damage models applied to the simulation of the mechanical behavior of bonded joints. Int J Adhes Adhes 28:419–426

    Article  Google Scholar 

  23. Roe KL, Siegmund T (2003) An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng Fract Mech 70:209–232

    Article  Google Scholar 

  24. Moroni F, Pirondi A (2011) A procedure for the simulation of fatigue crack growth in adhesively bonded joints based on the cohesive zone model and different mixed-mode propagation criteria. Eng Fract Mech 78:1808–1816

    Article  Google Scholar 

  25. Khoramishad H, Crocombe AD, Katnam KB, Ashcroft IA (2010) Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int J Fatigue 32:1146–1158

    Article  Google Scholar 

  26. Abaqus user manual, version 6.12, 2012

  27. Hobbacher A (2009) IIW recommendations for fatigue design of welded joints and components. WRC bulletin 520. The Welding Research Council, New York

    Google Scholar 

Download references

Acknowledgments

This work was supported by the Finnish Graduate School in Engineering Mechanics. Partial support was also provided by Ruukki Metals Oy and the Finnish Metals and Engineering Competence Cluster (FIMECC). CSC—IT Center for Science Ltd. is acknowledged for the allocation of computational resources.

Author information

Authors and Affiliations

  1. Department of Applied Mechanics, Aalto University, P.O. Box 14300, 00076, Aalto, Finland

    S. Hurme & G. Marquis

Authors
  1. S. Hurme
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. Marquis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Hurme.

Additional information

Doc. IIW-2472, recommended for publication by Commission XVI “Polymer Joining and Adhesive Technology.”

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hurme, S., Marquis, G. Fatigue experiments and finite element analysis of bolted/bonded double lap joints. Weld World 58, 771–785 (2014). https://doi.org/10.1007/s40194-014-0157-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40194-014-0157-4

Keywords

Search

Navigation