FormalPara Key Summary Points

Why carry out the study?

Patients undergoing cataract surgery who have previously undergone radial keratotomy (RK) face challenges in achieving accurate intraocular lens (IOL) power calculations due to altered corneal shape, necessitating a thorough evaluation of available calculation formulas.

The study aimed to assess the efficacy and predictability of 12 different IOL power calculation formulas in post-RK eyes, leveraging recent advances in technology and artificial intelligence (AI).

What was learned from this study?

AI-based formulas, particularly the Emmetropia Verifying Optical (EVO) 2.0 and Kane formulas, show promise in improving accuracy for post-RK eyes undergoing cataract surgery.

Established formulas like the American Society of Cataract and Refractive Surgery (ASCRS) and Barrett True K formulas remain effective options, while underutilized formulas such as the Equivalent Keratometry Reading (EKR) 65 and Camellin-Calossi formulas also demonstrate potential.

Panacea consistently underperformed compared to both established and newer generation formulas.

Introduction

During the 1970s and 1980s, radial keratotomy (RK), a refractive surgical procedure that involves making radial incisions in the cornea, emerged as a widely adopted surgical solution for myopia and astigmatism [1]. However, the refractive results of RK were highly variable, and were accompanied by numerous short- and long-term complications [2]. With the advent of excimer and femtosecond lasers in the late 1990s, more advanced corneal refractive surgeries replaced RK due to their improved predictability and safety [3]. As time has passed, a significant portion of the patient population that underwent RK has aged, resulting in an escalating number of post-RK eyes requiring cataract surgery.

Post-RK corneas pose unique challenges in eyes undergoing phacoemulsification. Specifically, RK alters normal corneal curvature, creates irregularities within the corneal surface, decreases the optical zone, and has been associated with diurnal variations in refraction. These factors create difficulty in determining the intra-ocular lens (IOL) power needed for cataract surgery and result in unexpected postoperative refractive outcomes. Specifically, the anterior–posterior corneal curvature ratio has been shown to decrease significantly after RK, which creates a challenge in calculating IOL power in post-RK eyes in comparison to virgin eyes [4]. As a result, the standard formulas developed to calculate IOL power for virgin eyes cannot be reliably employed to calculate IOL power in post-RK eyes because these formulas underestimate the IOL power, leaving the patient hyperopic [5].

Recent advances in topography/tomography devices have led to the development of more accurate measurements of true corneal power, which are particularly beneficial for post-RK eyes [6]. To aid in the calculation of IOL power in post-RK eyes, the American Society of Cataract and Refractive Surgery (ASCRS) has an online IOL power calculator specifically for post-RK eyes, which has been found to be a useful tool [7]. Additionally, evidence of fourth- and fifth-generation formulas, such as the Barrett True K formula, has been presented in current literature, showing an improved performance in reducing the mean absolute error (MAE) in the IOL calculation for post-RK eyes [8, 9].

Lastly, recent developments in artificial intelligence (AI) have led to the development of several AI-based IOL power calculation formulas, such as the Emmetropia Verifying Optical (EVO) 2.0, Kane, and Prediction Enhanced by Artificial Intelligence and output Linearization-Debellemanière, Gatinel, and Saad (PEARL-DGS) formulas. While these calculators have shown impressive results in reducing the MAE for both normal and atypical eyes, they have yet to be extensively reviewed in the literature [10, 11]. Other stand-alone formulas, such as the Camellin-Callossi and Panacea formulas, have been—and likely will continue to be—developed for this application so long as accuracy remains a concern.

Despite this extensive development of tools and methods, accuracy still poses a significant challenge, and further investigation is needed to assess the accuracy of these newly developed post-RK IOL calculation tools. Recently, an increasing number of studies have emerged to tackle this task, but many have yet to cover the breadth of formulas available for this purpose. In this context, the purpose of this study was to retrospectively assess the accuracy of 12 different formulas, both old and new, for IOL calculation in post-RK eyes. We also reviewed the relevant RK literature to compare the efficacy and predictability of these IOL calculations with those of our study.

Methods

A retrospective analysis was conducted on patients with a history of RK who presented for cataract surgery at Hoopes Vision Center, Draper, Utah (USA) between 2016 and 2023. This study was approved by The Biomedical Research Alliance of New York (BRANY) Institutional Review Board (#A20-12-547-823) and adhered to the tenets of the Declaration of Helsinki; it was also approved by the Hoopes Vision Ethics Committee.

This study included patients who had undergone uncomplicated cataract surgery, with a total of 37 eyes from 24 individuals. All cataract surgeries were performed by a single surgeon. Exclusion criteria included a history of laser-assisted in situ keratomileusis (LASIK) or refractive surgeries other than RK, complications post-phacoemulsification, post-RK wound complications, and insufficient preoperative and postoperative manifest refraction measurements taken at 6 months postoperatively.

Biometry measurements were taken using the Zeiss IOLMaster 700 version 1.90.12.05 (Carl Zeiss Meditec AG, Jena, Germany) and Lenstar 900 version i9.6.3.0 (Haag-Streit, Köniz, Switzerland) before cataract surgery. In cases where both devices provided biometric data, the values were averaged to ensure the most accurate measurements for subsequent calculations. Corneal topography was measured utilizing the Pentacam device (Optikgeräte GmbH, Wetzlar, Germany). Subjective refraction was obtained by experienced optometrists or ophthalmic assistants via phoropter at 6 m in the office at 6 months postoperatively.

A comprehensive literature review was conducted by two independent reviewers using the PubMED and Google Scholar databases for the period between 2016 and 2023. The initial search included the key terms 'IOL,' 'calculation,' and 'RK.' It was then broadened to include these key terms in conjunction with the names of the formulas utilized in this study. Selection of articles was guided by their relevance to the formulas in question and the adequacy of data evaluation. Exclusion criteria were applied to articles that did not employ the pertinent formulas or involved patients with RK alongside another prior refractive surgery, in alignment with the guidelines outlined by Wang et al. [12].

Surgical Procedure

A 2.4-mm clear corneal incision was created manually to avoid RK wounds. For patients with an increased risk of their RK incision opening with a corneal incision, a scleral approach was employed. Astigmatism of 0.1 was surgically induced. Duovisc (Alcon Laboratories, Inc., Fort Worth, TX, USA) viscoelastic was used. The surgeon performed a continuous curvilinear capsulorhexis ranging from 5.0 to 5.55 mm in size. Phacoemulsification, either in a horizontal chop or divide-and-conquer fashion, was carried out using the Infiniti Vision System (Alcon Laboratories, Inc). There were no complications related to the capsulotomy. Lenses were chosen by selecting the power that most closely approximated emmetropia, which was also the lowest myopic correction. All wounds were confirmed to be self-sealing.

Post-surgery, patients were instructed to use topical steroids 4 times a day, gradually tapering the dosage on a weekly basis over the course of 1 month. They were also advised to use topical non-steroid anti-inflammatory drug (NSAID) eyedrops twice daily for 6 weeks. Additionally, third- or fourth-generation fluoroquinolone antibiotic eyedrops were prescribed to be used 4 times daily for 1 week.

Formulas

The IOL power calculations were performed retrospectively utilizing 12 different formulas. The ASCRS calculation and the Barrett True K and Double K modified-Holladay 1 formulas were accessed from the ASCRS post-RK IOL online calculator (https://ascrs.org/tools/post-refractive-iol-calculator). This online calculator has the option to include pre- and post-RK refractive data, keratometry, axial length, anterior chamber depth (ACD), lens thickness, and white-to-white [13,14,15]. The Double K modified-Holladay 1 formula was also used in conjunction with the Holladay EKR65 values to yield an additional formula variation [16]. It should also be noted that the ASCRS calculation is reported as an average of the formulas utilized in the Barret True K, Double K modified-Holladay, and optical coherence tomography (OCT)-based calculations [17, 18]. In the online ASCRS calculator, the Double-K Holladay 1 formula takes into account the values from EyeSys effective refractive power (EffRP; EyeSys Vision LLC, Houston, TX, USA) and average central corneal power from the non-simulated keratometry (SimK) topography devices Atlas (Carl Zeiss AG, Germany), Pentacam (Oculus, Wetzlar, Germany), and IOLMaster/Lenstar (Carl Zeiss AG, Germany/Haag-Streit AG, Switzerland). In the clinic where the current study was performed, EyeSys EffRP, average central corneal powers from non-SimK values, and Atlas Ring 1-4-mm data were not collected for each patient. Therefore, an average of the Barret True K, OCT-Based, and Double K modified-Holladay formulas with optical biometry information from the Pentacam and IOLMaster/Lenstar systems was used.

For the EKR65 (Holladay) formula, K1 and K2 were calculated by using the aforementioned method, and values were taken based off a 4.5-mm pupillary zone. These can be used with any standard IOL calculation formula, but for the purposes of this study was isolated to the EKR65 (Holladay) formula [19].

The Haigis-L formula was accessed from the ASCRS post-myopic LASIK/PRK IOL online calculator (https://iolcalc.ascrs.org/wbfrmCalculator.aspx). This calculator had the option to include the aforementioned data, and keratometry, axial length, ACD, lens thickness, and white-to-white were utilized [20]. The Panacea formula was accessed via the Panacea IOL and Toric Calculator for MAC and has the option to include axial length, lens thickness, ACD, corneal posterior/anterior ratio (P/A) ratio, asphericity (Q), mean keratometry, and the IOL A constant (www.panaceaioltoriccalculator.com) [21]. All were used in its calculation. In this study, a0 was calculated using the preoperative ACD, axial length, and standardized a1 and a2 values equal to 0.1 and 0.4, respectively, by the ASCRS calculator. Customized a1 and a2 values are available for calculation but require a larger data set than was available for this study. The Camellin-Calossi formula was accessed online (https://3ccalculator.lasek.it) and gave the option to calculate IOL power using the K1, K2, AL, ACD, IOL constants, and the desired refraction [22]. Additional values were listed as optional and were omitted for the purpose of this calculation.

The EVO 2.0, Kane, and PEARL-DGS formulas were accessed from the European Society Of Cataract & Refractive Surgeons (ESCRS) online calculator (https://iolcalculator.escrs.org/). This online calculator included keratometry, axial length, ACD, lens thickness, central corneal thickness, white-to-white, and biological sex [10, 23].

The A-constants recommended by the EVO 2.0, Kane, and PEARL-DGS formulas were used for each lens type. For the TECNIS ZCB00 monofocal lens, recommended A-constants of 119.3, 119.36, and 119.3 were used for the EVO, Kane, and PEARL-DGS formulas, respectively. For the Bausch + Lomb enVista enhanced MX60E lens (Bausch + Lomb, Laval, QC, Canada), the recommended A-constant of 119.1 was used for each formula. For the AcrySof SN60WF lens (Alcon Laboratories, Inc.), the recommended A-constants of 118.93, 118.98, and 119 were used for the EVO, Kane, and PEARL-DGS formulas, respectively. For the remaining calculations, including the ASCRS calculation, and the Barrett True K and DK-Holladay formulas, recommended constants were not provided. Therefore, the suggested A-constants and SF constants were used by each lens’ manufacturer. This resulted in an A-constant of 119.3 and SF of 1.96 for the TECNIS ZCB00 monofocal lens (Johnson & Johnson Vision, Irvine, CA, USA); an A-constant of 119.1 and SF of 1.85 for the enVista enhanced MX60E lens; and an A-constant of 118.7 and SF of 1.81 for the AcrySoft SN60WF lens [8–11]. A K-index value of 1.3375 was utilized where required [24,25,26].

Methods of Comparison and Adjustments

Our methods were adapted from Wang et al. [ 12] and Moshirfar et al. [11]. Data collection and initial analysis were performed in Microsoft Excel (Microsoft Corp., Redmond, WA, USA).

To calculate the refractive predictive error (RPE), the predicted manifest refraction based on the implanted IOL power was subtracted from the actual postoperative manifest refraction at the latest post-operative date, which was at least 6 months postoperative. A negative RPE value indicates the true result is more myopic than the predicted refraction, whereas a positive RPE value indicates the true result is more hyperopic. For each formula, the average RPE across all patients was calculated to determine the arithmetic mean (AME) and its corresponding standard deviation. The maximum, minimum, and range RPE values were also recorded for each formula.

The refractive MEA and median absolute error (MedAE, respectively) were then calculated. The MAE was calculated as the average of absolute differences between actual and predicted refractive outcomes for each formula. Absolute errors do not follow a Gaussian distribution, and the MAE is impacted by outliers, so the MedAE was calculated, which represents the central location of the absolute errors and is less influenced by outliers. Both MAE and MedAE are important parameters to record as large deviations from the mean often represent poorer outcomes in cataract surgery [27].

In analyses of IOL power calculation of normal eyes, lens constant optimization is generally performed whereby the AME is reduced to 0. However, due to the high heterogeneity in post-RK eyes, optimized IOL constants are unlikely to be accurate and therefore optimization is not considered necessary. Optimization was not performed in this study, consistent with published reports in the literature [28, 29].

Our primary outcome measure was the MAE. The total number and percentage of eyes with RPEs within ± 0.50 D, ± 0.75 D, ± 1 D, and ± 2 D were also calculated.

Statistical Analysis

Statistical analysis was performed utilizing SPSS statistical software (IBM Inc. Armonk, NY, USA) and Microsoft Excel (Microsoft Corp.). Guidelines recommended by Wang et al. were followed to analyze and compare formula performance [12]. The Kolmogorov–Smirnov test was used to assess the normality of the data. The arithmetic predictive error was compared via the repeated-measure analysis of variance (ANOVA) and the Friedman test, and the Wilcoxon Signed Ranks test was used to analyze the differences in MAE between formulas. Due to the use of multiple statistical comparisons, the Bonferroni correction was used to reduce the risk of type I error and inter-eye variability was also accounted for [30]. Lastly, the differences in number of eyes with prediction errors within ± 0.50 D, ± 0.75 D, and ± 1 D between formulas were analyzed via Cochran’s Q tests. A P value < 0.05 was considered to be statistically significant for all tests. The power of the statistical analysis was calculated using G*Power software, with a one-tailed normal parent distribution using an A-Priori power analysis. Effect size ‘d’ was calculated as the test statistic divided by the square root of the sample size. A power of 80% was considered a large effect size and was achieved using a significance level of 5% and a sample size of 30 eyes [31].

Results

A total of 37 eyes of 24 patients were included in this study (Table 1). All 37 eyes were included in at least eight of the formulas, with 33 (89%) of the eyes included in all 12 formulas. Four eyes did not have the necessary Pentacam data available, resulting in four eyes excluded from the Potvin-Hill formula analysis and two from the EKR65 formula. Two eyes did not have OCT data and were excluded from the OCT-Based formula analysis. Three eyes did not have a P/A ratio or asphericity values and were excluded from the Panacea calculations.

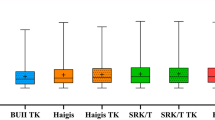
Table 1 Demographic and biometric data
Full size table

The AME, refractive prediction errors, MAE, and MedAE outcomes for each of the eight formulas were evaluated (Table 2). A significant difference in MAE was shown between the Panacea and ASCRS formulas (P < 0.05), between the Panacea and Barrett formulas (P < 0.05), and between the Panacea and the EKR65 variation of DK-Holladay formulas (P < 0.05); however, no additional differences were shown to be significant (Fig. 1). It should be noted that the same analysis using AME revealed a statistically significant difference in the following comparisons of formulas: Kane versus Potvin Hill (P = 0.042), Kane versus DK-Holladay (P = 0.021), Kane versus EKR65 Holladay (P = 0.018), Kane versus Haigis (P = 0.025), and Kane versus Panacea (P = 0.016). Cochran’s test also revealed a statistically significant difference between the ASCRS and EVO formulas (P = 0.046) in the percentage of eyes scoring within  ± 0.75 D of the target range, but no other differences were found to be significant.

Table 2 Measures of accuracy for the eight formulas in post-radial keratotomy eyes
Full size table
Fig. 1
figure 1

A 1:1 statistical comparison of each formula. Values in gray-shaded boxes indicate statistical significance.ASCRS The American Society of Cataract and Refractive Surgery, EKR65 EKR65 (Holladay), EVO Emmetropia Verifying Optical Formula 2.0, OCT optical coherence tomography, PEARL-DGS Postoperative spherical Equivalent prediction using Artificial Intelligence and Linear algorithms developed by Debellemaniere, Gatinel, and Saad

Full size image

The formula rankings of MedAE from least to greatest are as follows: Camellin-Calossi (0.515), ASCRS (0.535 D), EVO (0.545 D), Kane (0.555), Potvin-Hill (0.570), Panacea (0.579), EKR65 Holladay (0.584), DK-Holladay (0.603), OCT-Based (0.605), Haigis-L (0.629), and Barrett True K and PEARL-DGS (0.650).

The Kane formula achieved the greatest percentage of eyes within ± 1 D of the target range (75.68%), while the EVO 2.0 formula achieved the greatest percentage of eyes within ± 0.75 D of the target range (64.86%). The ASCRS, EVO, and Kane formulas performed similarly within ± 0.50 D of the target range, achieving 48.65% of eyes within this range (Table 3). It should also be noted the EKR65 Holladay formula achieved the greatest percentage of eyes within ± 0.25 D of the target range (35.14%) (Fig. 2).

Table 3 Percentage of eyes within prediction errors
Full size table
Fig. 2
figure 2

Refractive prediction error distribution. ASCRS American Society of Cataract and Refractive Surgery, EKR65 EKR65 (Holladay), EVO Emmetropia Verifying Optical Formula 2.0, IOL intraocular lens, OCT optical coherence tomography, PEARL-DGS Postoperative spherical Equivalent prediction using Artificial Intelligence and Linear algorithms developed by Debellemaniere, Gatinel, and Saad

Full size image

Discussion

This study aims to address gaps in the literature by providing a unique sample of IOL calculation formulas, encompassing fourth- and fifth-generation formulas such as the Barrett True K, established formulas such as OCT-based formulas, a combination of multiple RK-specific formulas (ASCRS), and AI-based formulas not specifically designed for post-RK eyes (Table 4).

Table 4 Summaries of recent studies comparing intraocular lens calculation formulas in post-radial keratotomy eyes
Full size table

The MAE in our analysis was found to be larger than what has been reported for AI-based formulas in previous studies. However, it is important to note that the MAE for the AI-based formulas in our study was comparable to that of the other formulas used. Therefore, for the following discussion, the focus will be on RPE for the AI-based formulas and a combination of MedAE and RPE for all other formulas. The culmination of our review of the literature and our analysis of our own results are discussed by formula in the following paragraphs.

The established formulas, including the Barrett True K, Potvin-Hill, and DK-Holladay formulas, the OCT-based formula, and the ASCRS calculation performed as expected, with the Barrett formula slightly outperforming the others. Though the difference in MAE between the Barrett formula and the others was not statistically significant (P = 0.441), the former achieved an impressive 32.43% of eyes within ± 0.25 D of the target range, 62.16% within ± 0.75 D of the target range, and 72.97% within ± 1 D of the target range. MedAE for the Barrett formula varies in the literature from 0.33 as reported by Turnbull et al. [29] to 0.77 as reported by Ma et al. [28], but in the present study it falls along the average reported MedAE at 0.65. Additionally, MedAE was shown to be lower in this study for the ASCRS calculation and the Potvin-Hill and OCT-based formulas, achieving 0.535, 0.57, and 0.605 respectively, as compared to values reported in the literature by Ma et al. [28] and Turnbull et al. [29], namely, 0.61, 0.632 and 0.77 respectively. Taken together, these data further support the use of the ASCRS calculation and its associated formulas in post-RK IOL calculation [6].

The EVO 2.0 formula, which is based on the theory of emmetropization, has displayed accuracy in extreme eyes [32]. The authors believe this formula, although not originally designated for post-RK eyes, demonstrated comparable accuracy to the ASCRS calculator due to this capability. It even surpassed the ASCRS calculation, achieving 64.86% of eyes within ± 0.75 D of the target range (P = 0.046), compared to ASCRS's values of 54.05% of eyes within ± 0.75 D of the target range (Table 3).

The Kane and PEARL-DGS formulas also showed promising results in post-RK IOL calculation, indicating the potential of these AI-based formulas [15]. An analysis of MAE did not differ significantly for either formula; however, an analysis of AME revealed that there was a statistically significant difference between the Kane and Potvin Hill (P = 0.042), DK-Holladay (P = 0.021), EKR65 (P = 0.018), Haigis (P = 0.025), and Panacea (P = 0.016) calculators. Kane outperformed each of these in the percentage ± 0.5 D, ± 0.75 D, and ± 1 D RPE categories, which is a notable correlation. Although intriguing, its performance was still not significantly different from that of ASCRS. The PEARL-DGS formula considers optical effects of lens thickness and shape factors, which may explain its better-than-expected performance in post-RK IOL calculation. These findings, especially those of Kane and EVO, corroborate the findings from Ferrara et al. [33] and may justify the use of these AI based formulas for this application.

The EKR65 formula yielded similar and statistically insignificant results [19]. MAE also did not differ significantly from that of the other accepted formulas, such as ASCRS, suggesting its potential applicability in post-RK eyes. The use of the EKR65 variation of the DK-Holladay formula has yet to be explored in the literature for this application. The results of the present study suggest that it may be worthy of further investigation due to this consistency that can be partially explained by its known characteristic of compensating for irregular posterior corneal curvatures in patients with keratoconus.

Conversely, the Panacea calculator, despite being included based on a recent study by Mena-Linares et al. [34], did not perform as well as other standardized formulas for post-RK IOL calculation. In contrast to the EVO 2.0 formula, Panacea achieved only 51.35% of eyes within ± 0.75 D of the target range and 62.16% of eyes within ± 1 D of the target range, contrary to the literature, suggesting its comparability to the Barrett True K formula [34]. The MAE was shown to be larger than that of ASCRS in this case as well (P = 0.01).

Utilization of the Haigis formula revealed findings in the present study that were comparable to those of Wang et al. [12], Leite de Pinho Tavares et al. [9], and Li et al. [8], but differed from Turnbull et al. [29], with the latter achieving 69.2% of eyes within ± 0.50 D of the target range, 86.5% of eyes within ± 0.75 D of the target range, and 92.3% of eyes within ± 1 D of the target range. In the Turnbull et al. study [29], the Haigis calculation was performed using both a standard approach and by using a - 0.50 D offset on target refraction, based on a study performed by Geggel et al. [35] who stated that it may be more accurate. The standard Haigis was found to be more effective, and its data were included in the present study. Consequently, it is difficult to draw a definitive conclusion as to precisely what the difference between our data and Turnbull et al.’s data [29] may have been. However, the results were comparable with the ASCRS overall, with 27.03% of eyes scoring within ± 0.25 D of the target range, 54.05% scoring within ± 0.75 D of the target range, and 72.97% scoring within ± 1 D of the target range. We speculate that this discrepancy from the literature might be due to variations in the calculation approach used in different studies. Further discussion and investigation are necessary to assess the effectiveness of the Haigis formula for post-RK eyes.

Lastly, the Camellin-Callosi formula showed promise in achieving the lowest MedAE of all the other formulas utilized, at 0.515. This formula was first developed in 2006 for IOL calculation following general refractive surgery, and it has since been evaluated in patients post-phototherapeutic keratectomy (PTK) and in normal cataractous eyes [36, 37]. However, its use following RK remains largely unexplored. Results from a 2006 study [22], which included eyes that had previously undergone different refractive surgeries, including PTK and RK, achieved 60% of eyes scoring within ± 0.50 D of the target range, 80% scoring within ± 1 D of the target range, and 93% scoring within ± 1.5 D of the target range. Our results did not entirely align with these findings, with 46% of eyes scoring within ± 0.50 D, 70% within ± 1 D, and 92% within ± 2 D of the target range, respectively. However, the results in the current study were shown not to differ significantly from ASCRS (P = 0.681), and its MedAE remains a noteworthy finding, indicating the need for future investigation for its use in this application. Preoperative and 6-month postoperative distance visual acuities are shown in Table 5.

Table 5 Preoperative and 6 month postoperative distance visual acuities
Full size table

This study has several limitations that should be taken into consideration when interpreting the findings. First, it could be said that our study has a relatively small sample size of 37 eyes and may not fully represent the diverse population of individuals with post-RK eyes undergoing cataract surgery. However, our sample size is well within the upper range of the current literature. Additionally, although all 37 eyes were included in at least eight of the formulas, only 33 (89%) of the eyes could be included in all 12 formulas due to missing data, potentially introducing selection bias, and further limiting the study's scope. As a single-center retrospective analysis, the study may be susceptible to both inherent biases in data collection and patient selection. Furthermore, the study did not explore potential confounding factors, such as age and number of RK incisions, which could influence IOL power calculations in post-RK eyes. Age was considered by stratifying the data based on number of incisions, but ultimately ignored due to its limitation on sample size. We note here that only two patients had more than 16 incisions, while 12 patients had no more than eight incisions. Most of our sample size (28 patients) had between 12 and 16 incisions. Our patient population was between the ages of 53 and 86 years with an average age of 69 years.

Some may argue that the use of different biometry devices may introduce variability in the accuracy of corneal measurements; however, we believe that using these two devices and averaging their results strengthens the accuracy of our measurements. Again, it should also be noted that the ASCRS calculation is reported as an average of the formulas utilized in the Barret True K, Double K modified-Holladay, and OCT-Based calculation methods, where the Double K modified-Holladay formula utilizes values from several devices, including EyeSys EffRP and average central corneal power from non-SimK topography devices, Atlas, Pentacam, and IOLMaster/Lenstar. For this study, an average of the three formulas was used for each patient in the reported ASCRS value, using only values gathered from Pentacam and IOLMaster/Lenstar. However, the result can vary greatly depending on the amount of data input in the online calculator, as the ASCRS value may still be reported with or without the inclusion of all values. For this reason, it is difficult to interpret its comparison in the existing literature, as other practices may include different data gathered from different device combinations. In addition, the three AI-based formulas employed in this study are not specifically designed for IOL calculation in eyes that have undergone RK procedures. However, the PEARL-DGS calculator includes a feature designated for "complex eyes," encompassing cases involving post-RK, post-myopic laser vision correction, post-hyperopic laser vision correction, post-implantable Collamer lens, and non-physiological corneas. It is noteworthy that, in our investigation, we did not utilize this option. Despite this, the proportion of eyes within ± 0.50 D and with ± 1 D of the target range using the PEARL-DGS calculator in our study aligns with a recent study conducted by Helaly et al. [38] that did incorporate the "complex eyes" option. Given the continuous updates with AI, further research regarding the accuracy of AI-based formulas in post-RK eyes is warranted. We also acknowledge that additional formulas, such as Ray Tracing, are available. However, our existing diagnostic devices provided us the ability to utilize all of the aforementioned formulas, while it did have the capability to utilize Ray Tracing.

Due to patients with RK inherently becoming increasingly hyperopic over time, some could argue that not following the patients for several years postoperatively may present another limitation to this study. While we acknowledge these hyperopic shifts, we feel that the 6-month postoperative refractions provided accurate results that reflect those reported in the current literature. Another limitation is that this study did not look at the diurnal variation in RK variability of correction from morning to evening among our cohort, which can confound results as patients with RK are more hyperopic in the morning and less hyperopic into the evening. Another limitation is our use of the data from both eyes for some patients, which some may say causes inter-eye variability. We acknowledge this; however, the data were included in order to maintain an adequate sample size for our analysis. Despite these limitations, the study serves as an important stepping stone in addressing the challenges of IOL power calculation in post-RK eyes, emphasizing the need for larger, multicenter studies with standardized approaches to validate and expand on the findings.

Conclusion

Despite the wide acceptance of the formulas discussed in the present study, accuracy has remained a concern. Overall, the results of this study affirm that established formulas, such as the Barrett True K and DK-Holladay formulas, as well as the ASCRS average calculation remain effective methods for determining post-RK IOL calculation. Our results are consistent with those reported in the current literature in this regard. Panacea and the EKR65 Holladay variation formulas are both under-reported in the literature for this application. Our study found that the Panacea calculator underperformed when compared with the more established formulas and that the EKR65 formula showed some promise, indicating that certain underutilized formulas may still prove advantageous. We also found that the newer age formulas, such as EVO and Kane, hold a slight superiority over some of the older established formulas. Lastly, the Camellin-Callossi calculator outperformed many old and new generation formulas and may prove to be a valuable resource for this application. Further studies with larger sample sizes will be needed to investigate the potential of these AI-based IOL calculation formulas as well as the Camellin-Callossi formula to confirm these results.