FormalPara Key Summary Points

Why carry out this study?

Refractive surprise is common after cataract surgery in people with high myopia.

Ocular biometry plays an important role in intraocular lens (IOL) power prediction.

The association between preoperative ocular biometry and postoperative prediction error has been unclear in patients with cataract and high myopia.

What was learned from the study?

Preoperative keratometry, anterior chamber depth, lens thickness, and axial length are possible error sources for IOL power prediction when Hoffer QST, Holladay 2, Holladay 2-NLR, Kane, T2, and VRF are used in high myopic eyes.

K6, Emmetropia Verifying Optical, Olsen, and Barrett Universal II displayed high accuracy in high myopia and were not influenced by preoperative biometry parameters.

Introduction

Currently, despite the wide application of optical biometry, some difficulties still exist in calculating and choosing an appropriately powered intraocular lens (IOL). Such difficulties have become more relevant with the increasing expectations of cataract surgery for achieving refractive accuracy. As shown by previous studies [1, 2], the IOL power calculation in patients with high myopia (HM) is especially challenging, as the refractive outcomes become less predictable in these patients, whose eyes are characterized by excessive elongation (axial length [AL] ≥ 26.50 mm) [3, 4].

The chance for refractive surprises in HM eyes is high for several reasons. First, traditional two-variable vergence formulas, such as SRK/T and Hoffer Q, depend on keratometry (K) and AL for effective lens position (ELP) prediction [5]. The absence of internal AL adjustments greatly affects the accuracies of these formulas in extreme ocular dimensions, such as HM cases. In addition, the calculation model used in two-variable and three-variable (Haigis) vergence formulas tends to overestimate K in long eyes [6], which further leads to unexpected ELP deepening and compromised predictive accuracy. Second, as a result of calibration of optical biometry to ultrasound immersion data [7], the ALs measured in people with high myopia may longer than they actually are. In addition, as nuclear opalescence is common in high myopic cataract [8], increased lens density in the visual axis could affect the group refractive index (GRI) and possibly give rise to inaccurate GRI-based AL measurements [9, 10]. As the precision of IOL calculation is essentially determined by the accuracy of the measurement of AL [7], inaccurate AL measurements in HM eyes are an important source of error in IOL power calculations. Third, the altered characteristics of the anterior segment in long eyes may interfere with the formulas’ assumptions of IOL power, which further results in inaccurate predictions.

Although some modern formulas have generally outperformed those of prior generations [1, 2], some of the newest formulas have yielded a prediction error (PE) beyond ± 0.50 D for more than 20% of patients with HM [11,12,13,14,15,16,17,18]. Therefore, for patients with HM, the refraction prediction performance of existing IOL power formulas remains far from perfect. Considering the important role of preoperative ocular biometry in ELP prediction and IOL power calculation [19], the biometric characteristics of HM eyes represent an important possible error source of IOL power prediction. However, for patients with HM, the influence of their biometric features on the predictive accuracy of different IOL power formulas has not been clarified thus far [20].

Therefore, we designed the present study to address two main questions: (1) What is the predictive accuracy of 10 currently popular IOL power formulas (the Barrett Universal II [BUII], Emmetropia Verifying Optical [EVO], Hoffer QST, Holladay 2, Holladay 2-NLR, Kane, K6, Olsen, T2, and VRF formulas) when calculating the IOL power for patients with HM? (2) How do certain ocular biometry parameters in patients with HM (AL, K, Q value, central corneal thickness [CCT], white-to-white [WTW], anterior chamber depth [ACD], and lens thickness [LT]) influence the predictive accuracy of the different formulas?

Methods

This study was approved by the Medical Ethics Committee of the Eye & ENT Hospital (Fudan University), Shanghai, China. Informed consent was obtained from all patients included in the study. The research protocols adhered to the tenets of the Declaration of Helsinki and its subsequent revisions.

Patients

This prospective cohort study comprised 202 cataractous eyes from 202 consecutive patients who underwent cataract surgery at the Eye and ENT Hospital, Fudan University (Shanghai, China). The inclusion criteria were (1) uneventful small-incision (≤ 2.6-mm-wide surgical wound) phacoemulsification cataract surgery with the insertion of one of the following six different IOL models: Zeiss CT Asphina 409 MP (n = 53), AMO Tecnis ZA9003 (n = 57), AMO Tecnis PCB00 (n = 23), HumanOptics MC X11 ASP (n = 25), Ophtec PC 525Y Ergomax (n = 13), and Rayner Superflex Aspheric 920H (n = 31); and (2) complete preoperative ocular biometry.

The exclusion criteria of this study included a history of contact lens wearing, corneal abnormalities, pterygium, glaucoma, uveitis, zonular weakness, lens luxation, diabetic retinopathy, invalid ocular biometry, missing postoperative refractive information, and postoperative corrected distance visual acuity (CDVA) less than 20/40. We ruled out patients who had undergone pterygium surgery [21], corneal refractive surgery [22], implantable collamer lens (ICL) implantation [23], or vitrectomy surgery [24]. These cases were excluded to avoid preexisting surgery-induced changes in ocular anatomical and optical properties. In addition, patients with pathological myopia featuring severe maculopathy were also excluded because of differences in the characteristics of their postoperative refractive success [25].

If both eyes with unequal CDVA in the same patient were eligible, the eye with better CDVA was selected. If both eyes with equal CDVA in one patient were eligible, the first eye that underwent cataract surgery was selected. After completion of consecutive enrollment and eye selection, the included eyes were divided into the HM group and the non-HM group according to their ALs [3, 4]. High myopia was defined as an AL exceeding 26.5 mm [3, 4].

Ocular Biometry Measurement

For all patients, ocular biometry was performed before surgery using an Oculus Pentacam HR (software version 1.25r15) for the Q value, a Tomey EM-3000 (software version 602-210S-2A5) for the CCT, and a Zeiss IOLMaster 700 (software version 1.88) for the AL, K, WTW, ACD, and LT. The Q value was assessed on the anterior corneal surface at the 6.0-mm-diameter aperture. Only the measurements with good quality indicators were considered qualified and used in this study.

IOL Power Calculation

The IOL power was calculated using 10 currently popular IOL power formulas: BUII, EVO, Hoffer QST, Holladay 2, Holladay 2-NLR, Kane, K6, Olsen, T2, and VRF. The EVO (available at https://www.evoiolcalculator.com/; accessed on 20 Sep 2023), Kane (available at https://www.iolformula.com/; accessed on 20 Sep 2023), K6 (available at https://cookeformula.com/Calculator; accessed on 20 Sep 2023), and Hoffer QST (available at https://hofferqst.com/; accessed on 20 Sep 2023) formulas are available on their respective websites. The T2 and VRF formulas were programmed into Excel spreadsheets [26, 27]. The BUII and Holladay 2 formulas are accessible via their respective Zeiss IOLMaster 700 software programs. The Olsen formula is available in a software package for IOL power calculation (PhacoOptics, IOL Innovations ApS, Aarhus, Denmark). We used the BUII formula as the actual formula for preoperative IOL power calculation.

Subjective manifest refraction was performed 1 month postoperatively. Then, the arithmetic PE was calculated as follows:

$${\text{Prediction error }}\left( {{\text{PE}}} \right) \, = {\text{ Actual postoperative refraction }}{-}{\text{ predicted refraction}}$$

PE was defined as positive for patients with hyperopic refractive outcomes and negative for patients with myopic refractive outcomes.

The Kane, K6, and EVO formulas were optimized by their corresponding authors. The Hoffer QST formula was optimized on its official website (available at https://hofferqst.com/; accessed on 20 Sep 2023) using the predefined Excel spreadsheet. During optimization, all recipients (including HM and non-HM recipients) of one certain IOL model were categorized into a subset and analyzed as a whole for optimization. The lens constant was modified, and for each IOL subset, the dataset was reran until the mean PE (MPE) equaled zero [1]. The new lens constants after optimization are presented in Table S1. After optimization, we calculated the median absolute error (MedAE) and mean absolute error (MAE) for the comparisons between different formulas.

Statistical Analysis

In this study, MAE and MedAE were used to compare the predictive accuracy between different formulas [1, 2], whereas PE was used to evaluate the predictive accuracy of the individual formulas, according to the method described by Savini et al. [28] The MAEs, MedAEs, MPEs, ranges of PE, standard deviations of the error (STDEVs), root mean square errors (RMSEs), quartiles of absolute error (AE), and skewness of AE are presented in Table 2.

First, to compare the predictive accuracy among the 10 formulas, we calculated and analyzed the MAE and MedAE using repeated-measures analysis of variance (ANOVA) and Friedman’s test, respectively. The Cochran’s Q test was employed to compare the percentage of eyes within 0.5 D and 1.0 D of AE [29]. If the null hypothesis was rejected, a post hoc analysis with Bonferroni correction for multiple comparisons was performed. G*power software (version 3.1.9.7, Faul, Erdfelder, Lang, & Buchner, 2020. Available at https://www.gpower.hhu.de; accessed on 26 Oct 2023) was used for post hoc power analysis of repeated measures [30].

Second, we used a multivariable linear regression model to assess the influence of the ocular biometry parameters on the predictive accuracy of each IOL power formula, according to the method described by Savini et al. [28] The dependent variable of the model was the PE of each formula after zeroing out the MPE. The arguments of the model included sex, age, AL, K, Q value, CCT, WTW, ACD, and LT. The linear regression coefficients (β values) and standardized β values were calculated using the regression model.

Data analysis was performed using IBM SPSS Statistics, version 23.0 (SPSS Inc., Chicago, Illinois, USA). P values were calculated using two-sided tests, and the significance threshold was set at 5% through all statistical analyses. The normality of the data was examined by the Kolmogorov-Smirnov test after zeroing out the MPE. The needed sample size was determined using G*power software [29, 30]. Given an effect size of 0.25, a significance level of 5%, and a test power of 95% [22], a sample size of 20 eyes would be necessary.

Results

Study Population

Our study comprised 202 eyes of 202 patients, including 108 HM eyes (53%) and 94 non-HM eyes (47%). Table 1 shows the demographics and biometry data of all patients. The mean age of all patients was 65.2 ± 11.3 years (median, 66.0 years; range, 30–97 years), and 61.9% were female. HM eyes had a mean AL of 30.30 ± 2.23 mm (median, 30.20 mm; range, 26.53–35.42 mm), a mean K of 44.0 ± 1.7 D (median, 43.8 D; range, 40.2–47.8 D), with a median IOL power of 7.0 D (mean, 7.3 ± 5.0 D; range, − 3.0–17.5 D), whereas non-HM eyes had a mean AL of 23.97 ± 1.31 mm (median, 23.85 mm; range, 21.11–26.46 mm), a mean K of 44.0 ± 1.3 D (median, 44.0 D; range, 41.4–47.1 D), with a median IOL power of 20.5 D (mean, 20.3 ± 3.1 D; range, 13.5–27.0 D).

Table 1 Demography and ocular biometry data of all cases, high myopic cases, and non-high myopic cases
Full size table

Comparison of Formula Performance

After the MPE was zeroed out, the PEs of the BUII, EVO, Hoffer QST, Holladay 2-NLR, Kane, K6, Olsen, and VRF formulas were normally distributed. In HM eyes, statistical analysis of the MAE with repeated-measures ANOVA showed a significant difference among all 10 formulas (P < 0.001). A significant difference was found predominantly between the formulas (EVO, K6, Olsen, and BUII) with the lowest MAEs (0.39, 0.41, 0.43, and 0.47, respectively) and the other six formulas (P < 0.05).

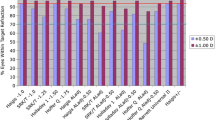
Comparison of the MedAE in HM eyes with Friedman’s test also significantly differed between all 10 formulas (P < 0.001). A significant difference was detected predominantly between the formulas (Hoffer QST, VRF, T2, and Holladay 2) with the highest MedAEs (0.45, 0.47, 0.48, and 0.61, respectively) and the remaining six formulas (P < 0.05). Figure 1 and Table 2 show the results of the 10 formulas in HM eyes. Figure 2 is a stacked histogram showing the percentages of patients within a given diopter range of the predicted refraction outcome among patients with HM. According to the results of post hoc power analysis, the power for repeated measures in the HM group was 93%.

Fig. 1
figure 1

Smoothed line graph showing the mean absolute errors and median absolute errors of the IOL power formulas in patients with high myopia. Error bars represent the 95% confidence intervals (BUII, Barrett Universal II; EVO, Emmetropia Verifying Optical; HQST, Hoffer QST; H2, Holladay 2; MAE, mean absolute error; MedAE, median absolute error; D, diopter)

Full size image
Table 2 Prediction performance of 10 intraocular lens power formulas in 108 patients with high myopia
Full size table
Fig. 2
figure 2

Stacked histogram showing the percentages of patients within a given diopter range of the predicted spherical equivalent refraction outcome among patients with high myopia. (BUII, Barrett Universal II; EVO, Emmetropia Verifying Optical; HQST, Hoffer QST; H2, Holladay 2; D, diopter)

Full size image

Cochran’s Q test in the HM group determined that there was a statistically significant difference in the constituent ratio of AE ranges between formulas (P < 0.001). BUII, EVO, K6, and Olsen yielded significantly more AE < 0.5 D than Holladay 2 (all P < 0.05). The proportion of AE exceeding 0.5 D when utilizing T2 and VRF was significantly higher than that when using EVO and K6 (all P < 0.05). For an AE greater than 1.0 D, it was more common when Holladay 2 and T2 were employed compared with calculations by EVO, K6, and Olsen (all P < 0.05).

In patients with HM with a K < 44.0 D, the K6 (MedAE, 0.29 D), Olsen (MedAE, 0.33 D), and EVO (MedAE, 0.34 D) formulas afforded the lowest MedAEs and outperformed the Holladay 2 (MedAE, 0.59 D) formula which had a significantly higher MedAE (all P < 0.05). In HM eyes with a K ≥ 44.0 D, the K6 (MedAE, 0.31 D), EVO (MedAE, 0.34 D), Olsen (MedAE, 0.37 D), and BUII (MedAE, 0.40 D) formulas showed significantly fewer MedAEs than the Holladay 2 (MedAE, 0.62 D) formula (all P < 0.05).

In non-HM eyes, repeated-measures ANOVA with post hoc analysis showed no significant difference in the MAE among all 10 formulas (P > 0.05). Additionally, analysis of the MedAE with Friedman’s test showed no significant difference among the 10 formulas (P > 0.05). According to the results of the post hoc power analysis, the power for repeated measures in the non-HM group was 90%. Cochran’s Q test determined that in non-HM eyes, the proportion of AE exceeding 1.0 D when using Holladay 2 was significantly higher than that when K6 was employed (P < 0.05).

In non-HM eyes with a K < 44.0 D, Friedman’s test determined no significant difference among the MedAEs of the 10 formulas (all P > 0.05). However, in patients without HM with a K ≥ 44.0 D, the BUII (MedAE, 0.37 D) and K6 (MedAE, 0.35 D) formulas had significantly lower MedAEs than the Holladay 2 formula (MedAE, 0.55 D) (all P < 0.05).

Relationship Between Ocular Biometry Parameters and Prediction Error

Figure 3 is a heatmap showing the Pearson’s correlations in HM eyes between the ocular biometry parameters and the PE of each formula. For HM eyes, there was a high correlation between a greater AL and a hyperopic outcome from the Holladay 2 formula (Pearson’s correlation coefficient [r], 0.62; P < 0.001). In addition, a more negative Q value in HM eyes was correlated with hyperopic outcomes from the Holladay 2 (r, − 0.28; P = 0.007) and T2 formulas (r, − 0.28; P = 0.007). In non-HM eyes, Pearson’s correlation analysis revealed a weak correlation between the LT and the PE of the VRF formula (r, 0.24; P < 0.05).

Fig. 3
figure 3

Heatmap analysis of the correlations between the ocular biometry parameters and prediction error of each IOL power formula in patients with high myopia. Data in the cells are Pearson’s correlation coefficients (BUII, Barrett Universal II; EVO, Emmetropia Verifying Optical; HQST, Hoffer QST; H2, Holladay 2)

Full size image

Table 3 summarizes the relationships of AL, K, ACD, and LT with the PEs of different formulas using the multivariable linear regression model. In HM eyes, a greater AL was associated with hyperopic refractive outcomes when using the Holladay 2 and T2 formulas (all P < 0.01) or myopic refractive outcomes when using the Kane, Hoffer QST, and VRF formulas (all P < 0.05). The formulas whose PEs had the strongest associations with AL were the Holladay 2 (β, 0.63) and Kane formulas (β, − 0.53) (Fig. 4a, b).

Table 3 Association between ocular biometry parameters and prediction error in 108 patients with high myopia
Full size table
Fig. 4
figure 4

a–e Scatter plots showing the correlations between the ocular biometry parameters and the prediction error in patients with high myopia (PE, prediction error; D, diopter)

Full size image

A hyperopic shift in HM eyes was also associated with a steeper K (for VRF, T2, and Holladay 2), greater ACD (for Kane, Holladay 2-NLR, Hoffer QST, T2, and Holladay 2), and larger LT (for Hoffer QST, Holladay 2-NLR, T2, and Holladay 2). The formulas whose PEs had the strongest association with the preoperative K, ACD, and LT were the VRF (β, 0.33), Kane (β, 0.38), and Hoffer QST formulas (β, 0.28), respectively (Fig. 4c–e). The multivariable model also revealed that WTW, CCT, and Q value had no association with the PE of any formula in the patients with HM (all P > 0.05).

According to multivariable linear regression analysis, the associations between the ocular biometry parameters and PEs that were significant in HM eyes were not present in patients without HM (all P > 0.05).

Discussion

Here, we showed that the K6, EVO, Olsen, and BUII formulas showed high accuracy in HM eyes. The accuracies of the K6, EVO, Olsen, and BUII formulas were not influenced by ocular biometry parameters. For the remaining six formulas, the preoperative K, ACD, LT, and AL were possible errors of the IOL power prediction in patients with HM.

Considering the wide variability of refractive outcomes in HM eyes [6], it is currently challenging for most ophthalmologists to choose the right IOL power formula for patients with HM, since recent studies [11,12,13,14,15,16,17,18] have demonstrated conflicting results. According to our study, we recommend the K6, EVO, Olsen, and BUII formulas for calculating the IOL power in HM eyes. The high precision of the EVO, Olsen, and BUII formulas in people with high myopia largely mirrors the findings of some recent studies [11,12,13].

According to several large cross-sectional studies [31,32,33], a greater AL was associated with lower K [31], wider WTW [32], and deeper ACD [33] in eyes with normative axial dimensions. However, the linear association between AL and K was absent when AL was greater than 28.00 mm [34]. Additionally, shallow ACD was identified in subjects with HM even with long ALs [35]. Moreover, as AL increased, the change in WTW was nonlinear, which was the same as the trend of the LT variation with ocular elongation [36]. Consideration should be given to ocular biometry alterations when calculating IOL power in high myopia.

AL is one of the most basic metrics used in IOL power formulas. Despite the constant optimization, Holladay 2 still predicts hyperopic shifts in patients with HM. In contrast, modern formulas, such as the Kane and VRF formulas, may tend to undercorrect when calculating the IOL power for long eyes to cope with the unwelcomed hyperopic shift, which is common in patients with HM [6].

It was interesting to find a relationship between the LT and the refractive outcomes of the Holladay 2 and Holladay 2-NLR formulas, as they have used the preoperative LT for calculation. According to a study by Satou et al. [37], the actual IOL position was effectively predicted by the equatorial surface depth and posterior surface depth of the crystalline lens rather than its thickness. Thus, there may be other lens biometry parameters that are more helpful than LT for predicting the ELP. According to previous findings [19], the influence of IOL position on postoperative PE was greater in normal eyes than in high-myopic eyes. A better integration of preoperative lens biometry for ELP prediction may greatly improve refractive outcomes in eyes with normative axial dimensions.

The IOLMaster 700 measures K using three different zones of the cornea. Thus, Q values are implicitly included in the K readings of the IOLMaster 700. An accurate measurement of the preoperative Q value is helpful for improving the predictive accuracy [38]. However, in our study, no relationship was found between the preoperative Q value and postoperative PE in HM eyes. According to previous large cross-sectional studies [39, 40], the Q value had a significant direct relationship with the K readings. Preoperative K is known to cause a trend error in the Haigis and SRK/T formulas in normal eyes [1, 41]. Whether the Q value was adjusted by K as a confounder in the multivariable model or whether the pattern by which the Q value and K influence IOL power in long eyes is different from that in normal eyes can only be confirmed by further studies.

Our study had several limitations. First, the optimization performed in this study is only for clinical research purposes to investigate the influence of ocular biometry on the formulas’ predictive accuracy. We did not perform an “overall optimization” of the formulas, which would be systematic work requiring a larger sample size and enough subjects from the whole AL spectrum [29]. Further investigations using lens constants from a group of normal eyes may be helpful to validate our findings. Second, more than one IOL model was used in this study, which may raise the degree of bias and affect the results of the correlation analysis. Although the MPE was zeroed separately for each IOL model, following the method described by Melles et al. [1], it would be preferable to use a single IOL model throughout the study. Third, our survey is a single-center hospital-based study with a limited sample size (total N = 202). Our study setting may enhance selection bias, which possibly gave rise to unsatisfactory normality of PE values calculated by Holladay 2 and T2. Further population-based studies with extensive sample enrollment are helpful in verifying our findings. Fourth, some new formulas, such as the Hill-RBF 3.0, PEARL-DGS, and Panacea formulas, are also attractive modern formulas deserving comprehensive investigation. However, as a result of limited space in one single paper, we confined the range of the present study to an evaluation of 10 formulas. Other new formulas, which were not included in this study, will be studied in our further survey.

Conclusions

The K6, EVO, Olsen, and BUII formulas achieved satisfactory results in HM eyes and were not influenced by preoperative ocular biometry parameters. The preoperative K, ACD, LT, and AL were possible error sources for IOL power prediction when using the Hoffer QST, Holladay 2, Holladay 2-NLR, Kane, T2, and VRF formulas in patients with HM. Our findings may provide information on the choice, optimization, improvement, and development of IOL power formulas with high predictive accuracy for patients with HM.