Introduction

Given the occurrence of destructive earthquakes in seismically intensive regions, the resultant human and financial losses, and the scientific inability to predict earthquakes, investigations into earthquake early warning systems (EEWSs), and their development are critical requirements. Accordingly, researchers have recently proposed many approaches to improving EEWS performance [1, 3, 4, 12, 14, 15, 17, 26, 27, 29]. Earthquake records generally contain valuable information on seismic sources [20]; records of the first waves of an earthquake contain information on magnitude, and those of second waves carry information on energy [2, 12]. For this reason, source parameters (magnitude and location) in EEWSs are estimated through an analysis of the initial phases of P-wave arrival. Because the frequency content carried by the initial seconds of a signal does not depend on epicentral distance, earthquake magnitude can be directly estimated using frequency parameters without correcting distance effects [6, 24, 25, 28]. This method enables the derivation of empirical magnitude–scaling relationships in EEWSs on the basis of frequency information from the first few seconds of P-wave arrival [1, 2, 6, 12, 16, 21,22,23,25, 28]. In this regard, two basic parameters, namely, \(\tau_{\text{P}}^{ \hbox{max} }\) and \(\tau_{\text{c}}\), were introduced for use in EEWSs in California [5, 13]. In the \(\tau_{\text{P}}^{ \hbox{max} }\)-based method proposed by Nakamura [16], \(\tau_{P}\) is measured through acceleration and velocity time series within the initial seconds of receiving P-waves (usually 3–4 s); the calculation proceeds as follows [1]:

$$\tau_{\text{P}} = 2\pi (X_{i} /D_{i} )^{1/2}$$
(1)
$$X_{i} = X_{i - 1} + x_{i}^{2}$$
(2)
$$D_{i} = D_{i - 1} + (\partial x/\partial t)_{i}^{2} ,$$
(3)

where i denotes the number of samples, \(x_{i}\) is the ground motion velocity within a sampling interval, \(X_{i}\) represents the smoothed ground velocity squared, \(D_{i}\) is the time derivation of the ground velocity (acceleration), and α stands for the smoothing regularization constant. Variable α is set to \(1 - (1/F_{\text{s}} )\). Allen and Kanamori [1] considered \(\tau_{\text{P}}^{ \hbox{max} }\) the maximum value of \(\tau_{\text{P}}\) within 2–4 s after P-wave arrival. The \(\tau_{\text{P}}\) measured within the initial seconds of P-wave arrival can be disregarded, because this parameter depends largely on pre-signal noise level [18, 19] [21]. Frequency parameter \(\tau_{\text{c}}\), proposed by Wu and Kanamori [24] for scaling earthquake magnitude, is calculated by thus:

$$\tau_{\text{c}} = 2\pi /\sqrt r$$
(4)
$$r = \mathop \smallint \limits_{{t_{0} }}^{t} v^{2 } (t){\text{d}}t/\mathop \smallint \limits_{{t_{0} }}^{t} u^{2} (t){\text{d}}t,$$
(5)

where \(u\) and \(v\) denote the displacement and velocity records of ground motions, respectively. The main weakness of \(\tau_{\text{P}}^{ \hbox{max} }\) and \(\tau_{c}\) theories is that they are justifiable for noise-free monochromatic signals [12, 18, 23, 29], yet an earthquake time series encompasses a wide range of frequencies characterized by unavoidable noise. Shieh et al. [21] indicated that \(\tau_{\text{P}}^{ \hbox{max} }\) is sensitive to the initial noise level of a signal. In an analysis of the underlying theory and characteristics of \(\tau_{\text{P}}^{ \hbox{max} }\), Wolfe [23] demonstrated that this parameter is a non-linear function of spectral amplitude and that it assigns considerable weight to high frequencies. Magnitude estimation grounded in \(\tau_{\text{P}}^{ \hbox{max} }\) is, therefore, probably associated with significant errors. As Wolfe [23] proposed, wavelet and multi-taper concepts can be used to decrease the weighted dependence of \(\tau_{\text{P}}^{ \hbox{max} }\) on frequency contents and precisely determine the correlation between \(\tau_{\text{P}}^{ \hbox{max} }\) and earthquake size. To define a new frequency parameter, namely, the log-average period (\(\tau_{ \log }\)), Ziv [29] used the power spectrum of a signal in the initial seconds of P-wave arrival. \(\tau_{ \log }\) is measured on the basis of the early proportion of the velocity spectrum as follows: (a) the initial few seconds of P-wave arrival are extracted from the total waveform, (b) the effects of a windowed signal on two ending edges of the signal are eliminated using a Hanning window, (c) power spectrum coefficient \(P_{i} \left( {\omega_{i} } \right)\) is calculated on the basis of Fourier transform, and (d) the \(\tau_{ \log }\) value is measured through the following equation:

$$\log (\tau_{\log } ) = \frac{{\mathop \sum \nolimits_{i} P_{i}^{*} \left( {\omega_{i} } \right)\log \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\omega_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\omega_{i} }$}}} \right)}}{{\mathop \sum \nolimits_{i} P_{i}^{*} (\omega_{i} )}},$$
(6)

where * shows that \(P_{i} \left( {\omega_{i} } \right)\) is resampled per 0.1 log unit of frequency within frequency ranges of 0.1–10 Hz. At the end of the calculation, the logarithm of the average \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{ \log }\) measurements of each event are plotted against earthquake magnitudes, and the best line is fitted using the least-squares method as follows:

$$M = a \log \left( \tau \right) + b \pm \sigma .$$
(7)

Earthquake early warning systems use this logarithmic–linear relationship in estimating earthquake magnitude. In this relationship, \(a\) and \(b\) denote linear regression coefficients, and \(\tau\) and \(M\) denote the frequency parameter and magnitude, respectively. We introduced a new magnitude-scaling parameter called \(\tau_{\text{fcwt}}\), which is based on time–frequency continuous wavelet transform (CWT) as a combination of spectral methods and wavelet transform.

Data

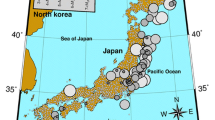
The data catalogue treated in this work consisted of vertical component accelerograms associated with 72 earthquakes with magnitudes (\(M_{\text{JMA}}\)) between 3 and 8 and epicentral distances smaller than 100 km. The data are also related to the borehole accelerometers recorded in the KiK-net strong-motion seismograph networks of Japan’s National Research Institute for Earth Science and Disaster (NIED) Prevention from 2000 to 2016 (Fig. 1). Vertical borehole records were used to eliminate near-surface effects. To reduce undesirable effects from background noise, records with high signal-to-noise ratio (> 5) were chosen among the vertical components. This ratio indicates the power of the main signal-to-background noise power. It is clear that a greater amount of this ratio represents the high quality of the seismic signal. Moreover, the earthquakes chosen were those occurring from inland and oceanic rim events with focal depths of less than 50 km. The data set likewise included the broadband signals of strong ground motion with a sampling frequency of 100 or 200 Hz.

Fig. 1
figure 1

Black circles show the epicenter of 72 studied earthquakes. The size of the circles corresponds to earthquake magnitude. All the earthquakes had a focal depth of less than 50 km; they occurred from 2000 to 2016 and were recorded in KiK-net

Full size image

Method based on \(\tau_{\text{fcwt}}\)

Similar to Ziv [29], we used the power spectrum of a signal within the first few seconds of P-wave arrival to determine the frequency features of the signal. However, Ziv [29] used Fourier transform to determine the power spectrum, similar to Atefi et al. [3], we adopted wavelet transform coefficients \({\text{C(}}\lambda ,\tau )\) for such calculation [3]:

$$C(\lambda ,\tau ) = \mathop \smallint \limits_{ - \infty }^{ + \infty } f\left( t \right)\psi_{\lambda ,\tau }^{*} \left( t \right){\text{d}}t,$$
(8)

in which \(\psi_{\lambda ,\tau } (t) \equiv \frac{1}{\sqrt \lambda }\psi \left( {\frac{t - \tau }{\lambda }} \right)\) indicates the wavelet function, * shows the complex conjugate operation, \(\lambda\) is the scale factor, and \(\tau\) denotes the translation controller in time. Different values of \(\lambda\) indicate stretched and compressed values of the wavelet family for improved correlation with the \(f\left( t \right)\) signal in low and high frequencies. The wavelet transform of a time–frequency \(f\left( t \right)\) (here, the initial few seconds after P-wave arrival) is defined as the inner product of \(f\left( t \right)\) and \(\psi\) (wavelet family), resulting in wavelet coefficient \(C\). This time–frequency transform of \(f\left( t \right)\) was formulated as Eq. (8) [7,8,9,10,11]. In this study, the average of all the samples of the wavelet transform coefficients was used to estimate the power spectrum at each scale of \(\lambda_{0}\). In general, \(\tau_{\text{fcwt}}\) values are measured as follows. (1) After the removal of a trend and mean, a Butterworth bandpass filter with cut-off frequencies of 0.1 and 10 Hz is applied to acceleration signals, and then, 4-s time windows are eliminated after obtaining P-waves from records. (2) To eliminate sudden cutting effects on two ends of a windowed signal, a cosine taper of 0.05 is applied on the signal. (3) Windowed signals are decomposed using wavelet transform (Eq. 8), and \({\text{C(}}\lambda ,\tau )\)s are calculated in the 1024 scale of \(\lambda\). Daubechies-12 is used for the frequency analysis of the signals. Subsequently, (4) a pseudo-frequency is calculated using the f = Fc/(λ × Δ) relation, in which Fc is the central frequency of the wavelet function, and Δ represents the sampling periods. The average power spectrum for each pseudo-frequency is calculated using the following equation:

$$P(f_{i} ) = \frac{{\mathop \sum \nolimits C^{2} (f_{i} ,\tau )}}{N},$$
(9)

where \(N\) denotes the number of \(C(f_{i} ,\tau )\) coefficients. (5) Finally, \(\tau_{\text{fcwt}}\) is the inverse of the pseudo-frequency, which has the highest value of \(P(f_{i} )\). To obtain the empirical magnitude–scaling relationship, the logarithm of the averaged \(\tau_{\text{fcwt}}\) measurements of each earthquake record is plotted against magnitude. Then, the best line is fitted to the measurements using the least-squares method. Atefi et al. [3] introduced a wavelet-based proxy, log-averaged scale λlog, using weighted average power spectrum of different scales to obtain empirical magnitude–scaling relationship. In this study, we use frequency values which have maximum power spectrum. To better cooperation, we use the same database used in Atefi et al. [3].

Results

Figure 2 presents the results obtained on the basis of \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\) in the 4-s time window. The figure shows the logarithm of the \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\) measurements against magnitude (gray circles). Obtaining a suitable empirical magnitude-scaling relationship necessitates the use of the average frequency parameters related to records of each earthquake. Correspondingly, the average values of the frequency parameters are plotted using black circles in Fig. 2. The best regression line was fitted to the logarithm of the event-average values of \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\) and earthquake magnitude through the least-squares method. The constant coefficients of \(a\) and \(b\) associated with the best fitted line (Eq. 7) are listed in Table 1. The mean and standard deviation of the difference between observed and estimated magnitude \(|M_{\text{est}} - M_{\text{obs}} |\) residuals were used to verify the accuracy of the proposed \(\tau_{{f{\text{cwt}}}}\) relationship. Figure 3 and Table 1 present the residuals against the observed magnitudes of earthquakes. The results showed that the mean residuals were 0.45 ± 0.43, 0.49 ± 0.36, and 0.66 ± 0.59 magnitude units in the 4-s time window, as determined by \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\), respectively. To further evaluate the accuracy of the results for earthquakes with \(M <\) 5.5, the mean and standard deviation of the residuals were separately derived (Table 1). The \(\tau_{p}^{ \hbox{max} }\)-based method was more precise for earthquakes with \(M <\) 5. The \(\tau_{{f{\text{cwt}}}}\)-based approach exhibited more acceptable precision in determining the magnitudes of medium- and small-scale earthquakes than did the conventional \(\tau_{\text{c}}\)-based method.

Fig. 2
figure 2

Relationship between the measured periods and earthquake magnitudes within the 4-s time window. The individual measurements and the mean values are shown using gray circles and black points from top to bottom for \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\). The black line is the line that best fits the mean values

Full size image
Table 1 Mean and standard deviation of the difference between the observed and estimated magnitudes and the constant coefficients of a and b
Full size table
Fig. 3
figure 3

Observed and estimated magnitude differences in the 4-s time window after P-wave arrival. The difference between the magnitudes is calculated using \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\) which are represented by solid gray circles, hollow black squares, and solid black triangles, respectively

Full size image

Conclusion and discussion

Earthquake early warning systems use the frequency information of ground motion within the first few seconds of P-wave arrival in estimating earthquake magnitude. To this end, \(\tau_{\text{P}}^{ \hbox{max} }\)- and \(\tau_{\text{c}}\)-based methods were proposed. However, these parameters were formulated on the basis of assumptions that are acceptable for monochromatic and noise-free signals. In other words, the parameters tend to be biased toward high frequencies. Therefore, magnitude estimations, particularly for areas with high noise levels, are associated with unavoidable errors. To improve the accuracy of magnitude estimation on EEWSs, we developed a new frequency-based parameter called \(\tau_{{f{\text{cwt}}}}\) using CWT as a tool for extracting the frequency contents carried by the first few seconds of P-wave arrival. For comparison, \(\tau_{\text{P}}^{ \hbox{max} }\) and \(\tau_{\text{c}}\) parameters were also measured using the same database for \(\tau_{{f{\text{cwt}}}}\). In general, three empirical magnitude–scaling relationships were extracted using \(\tau_{\text{P}}^{ \hbox{max} }\), \(\tau_{\text{c}}\), and \(\tau_{{f{\text{cwt}}}}\) at a 4-s time window. These relationships were as follows:

$$log \left( {\tau_{\text{P}}^{\hbox{max} } } \right) = \, 0.245 \, M_{\text{JMA}} - \, 1.572$$
(10)
$$log \, \left( {\tau_{\text{c}} } \right) = \, 0.121 \, M_{\text{JMA}} \, - \, 0.658$$
(11)
$$\log \, \left( {\tau_{\text{fcwt}} } \right) = \, 0.138 \, M_{\text{JMA}} \, - \, 1.259.$$
(12)

To compare the precision of relations (10)–(12), the average residuals for earthquakes with MJMA < 5.5 were calculated (Table 1). The \(\tau_{\text{P}}^{ \hbox{max} }\) parameter appeared to be more sensitive to magnitude ranges of earthquakes than were τfcwt and \(\tau_{\text{c}}\) (Fig. 3, Table 1). The values calculated using \(\tau_{{f{\text{cwt}}}}\) within 4 s were plotted against the calculated values at time windows of 2 and 3 s for comparison (Fig. 4). As expected, the values were close to one another for small values of \(\tau_{{f{\text{cwt}}}}\) (frequency content of small earthquakes). For larger values of \(\tau_{{f{\text{cwt}}}}\) (frequency content of large earthquakes), the calculated values clearly differed (particularly those calculated within 2 and 4 s). We can conclude that \(\tau_{{f{\text{cwt}}}}\) was positively correlated with magnitude. Therefore, given that the magnitude ranges of the earthquakes studied reached 8.0, relations for estimating the magnitude obtained at 4 s were proposed (relations 10–12). The \(\tau_{\text{P}}^{ \hbox{max} }\)- and \(\tau_{\text{c}}\)-based methods calculate the frequency content carried by a signal using two components of records, whereas the \(\tau_{{f{\text{cwt}}}}\)-based approach uses only a single component of acceleration. Nevertheless, processing is more complex and time-consuming with the use of \(\tau_{{f{\text{cwt}}}}\) (because of its inherent CWT). This challenge can be overcome by upgrading hardware and using powerful processing systems. In general, the precision of this parameter can be evaluated through early warning systems across the world.

Fig. 4
figure 4

Comparison of the mean values of \(\tau_{{f{\text{cwt}}}}\) in the 4-s time window with those derived in the 2- and 3-s time windows

Full size image

Data and resources

The used records are obtained from KiK-net on-line databases. Figures are prepared using Generic Mapping Tools ([22]; last accessed August 2016). Data processing is performed using Seismic Analysis Code (https://ds.iris.edu/ds/nodes/dmc/software/downloads/ sac, last accessed May 2014).