Introduction

Competitiveness in the business market, improvement, and profitability is the main goals of each manufacturing firms. To achieve these goals, they need to adapt themselves to business market conditions (Valipour et al. 2013, 2016). In the 21st century, a business environment can be described by extending the universal competition and customer-oriented resulting in high variety and low demand. Nowadays, consumers need both low cost and high quality simultaneously. From the customers’ perspective, a manufacturing firm should meet even the least market demand with best price and quality. The group technology (GT) or cellular manufacturing (CM) concept can be used at manufacturing systems with high variety and low demand to get superiority to environments with low variety and high demand. GT is a manufacturing technique, so that the parts with the same characteristics are grouped and a set of machines are assigned to these groups to process these parts (Singh and Rajamani 2012).

GT introduced by Mitrofanov (1966) can be defined by matching and classifying the parts into several families based on common characteristics of them. On the other hand, the machines are classified into several cells, to process part groups simultaneously. In fact, GT is a link between job shop and flow shop environments. This technology offers the possibility of manufacturing a wide variety of products in a low volume. GT facilitates the control of a big system by dividing this to several sub-systems. This technology has a significant impact on optimal production in terms of increasing the production flexibility, decreasing the setup costs and products flow (Jouzdani et al. 2014).

CM is one of the main applications of GT, where the parts grouped as part families are processed by groups of machines in a cell. The determination of producing part families with groups of machines is known as cell formation problem (CFP). CM has several advantages including more flexibility in producing of new parts, reducing the work-in-process (WIP), reducing required times for production (Heragu 1994; Wemmerlöv and Hyer 1989), reducing material handling costs and setup time, and increasing the production volume, profitability, and quality (Wemmerlöv and Hyer 1989). It should be noted that CFP is known as an NP-hard problem that has been approved in the literature (Ballakur 1985).

Because of the importance of CFP, many researchers have shown their interests to this area of knowledge and investigated the different viewpoints toward it (Reisman et al. 1997; Selim et al. 1998; Yin and Yasuda 2006). Furthermore, different methods have been used in CF such as visual inspection, coding, and classification (Singh and Rajamani 2012), similarity coefficient method (Yin et al. 2005), graph theory approach (John et al. 2009), mathematical programming model (Mahdavi et al. 2010), soft computing (Venkumar and Haq 2006), fuzzy-based technique (Li et al. 2007), and neural networks (Malavé and Ramachandran 1991; Venkumar and Haq 2006, b).

Cao and Chen (2004) developed a taboo search (TS) method to solve CFP. The objective function was to minimize inter-cell movement, setup, and machine operating costs. In their paper, the machine capacity constraint has been considered (Cao and Chen 2004). Nsakanda et al. (2006) solved a CFP with respect to multiple routes for parts by genetic algorithm (GA) (Nsakanda et al. 2006). Wu et al. (2009) presented a simulated annealing (SA) composed with the mutation to solve a CFP with alternative processing routes (Wu et al. 2009). Paydar and Sahebjamnia (2009) proposed a linear programming model to determine part families and machine grouping in a CFP with respect to scheduling problem simultaneously (Paydar and Sahebjamnia 2009). Chung et al. (2011) also solved CFP by SA, so that they considered alternative routes as well as machine reliability (Chung et al. 2011). Mahdavi et al. (2012) proposed a mathematical model considering a three-dimensional incidence matrix of machine-part-worker (Mahdavi et al. 2012). Yadollahi et al. (2014) developed a single objective mathematical model with respect to machines’ breakdown (Yadollahi et al. 2014). Jouzdani et al. (2014) proposed a mathematical model with alternative processing routes and machine reliability which is solved by improved SA (Jouzdani et al. 2014).

Many researchers assume that each part has a unique process routing. However, it is known that a part may be processed via alternative routes in any level of the production plan (Lozano et al. 1999). Considering the existence of routes, the CFP is transformed into a generalized CFP (Kusiak 1987). The alternative routings may result in additional flexibility in the CM system design. Furthermore, papers associated with breakdown and machines’ reliability in CFP are scarce (Das et al. 2007; Diallo et al. 2001; Ameli and Arkat 2008; Logendran and Talkington 1997; Zakarian and Kusiak 1997). This is common that all of the machines are assumed that have 100% reliability in CFP. However, this assumption is not logical in the real-life manufacturing systems. The machine breakdown can affect extremely on system performance and increase completion time over due date. Therefore, in CMS design, the machine breakdown should be taken into consideration to promote the system performance. In addition, the reliability of the machines becomes more important when each part has several routes and this can be influential on decision making for determining the part routes (Jouzdani et al. 2014). Another important issue is tools’ allocation to machines and incurred costs based on changing the tools. Another important issue is the tools’ assignment to machines and calculates the tools’ substitution cost on machines. In CMS design, when the parts can be processed by various tools on machines, the change ability of tools on machines will play a key role in decisions that is related to determining the processing route for parts and imposed costs into system. Thus, the tools’ existence and the change ability of them on machines are considered in this research. Another case which is considered in this paper is the demand number for each part. In this paper, inter- and intracellular movements as well as tool replacement on machines is based on sequence of operations for each part. In other words, the sequence of operations is very important for calculating movement, routes’ setup costs, tools’ replacement, and machines’ breakdown.

Table 1 extracted from Jouzdani et al. (2014) reviews the several recent researches in CFP. As it is seen in this table, the tool assignment distinguishes this research from the previous papers.

Table 1 Brief review of related works in the literature (from 2005 to 2014)
Full size table

Since there is a variety in production parts in factories, CMS can save time and cost and thus increasing productivity by processing similar parts by machines which are located in separate cells. Therefore, this research is considered some key parameters such as moving parts path, tools’ existence, and reliability for machines in production cells. It helps which the CMS to be practical as well as it considers the change ability of tools on machines. Therefore, it prevents the moving of parts on different machines. In some industries, the parts which have weight or high volume the tools’ substitution on machines for doing several different processes by machines can be useful.

After checking research done by the other authors and latest papers, we understood that ability to install and replace tools on machines in CMS is a weakness in the previous researches. Therefore, in this research it is considered and is focused to investigate tools in CF which is as innovation this paper. This study develops the paper that is presented by Jouzdani et al. (2014) and Ameli et al. (2008). In this paper, tools’ assignment to machines and its substitution costs are considered as key factor in CFP. Moreover, to reaching to cost minimum, B&B method is proposed.

Problem description

In this study, a CFP is formulated as a linear integer-programming problem including inter- and intra-cell movements, routes’ selection costs, alternative processing routes, tools’ allocation, and machines’ reliability. Furthermore, the processing time of each operation for each part on each machine in each route with each tool is known and deterministic. The capability of processing for each operation on each tool located on each machine in each route is given. The number of various tools for different machines is known and finite when a tool changing on machine \(j\) is done that operation \(s\) from part \(i\) on machine \(j\) in cell \(k\) with tool \(t\) is done and operation \(s + 1\) from the same part \(i\) on the same machine \(j\) in the same cell \(k\) with tool \(t^{\prime}\) is done.

Furthermore, the parts can be moved within and between cells. When the subsequent operations for a part should be processed in two different cells, an inter-cell movement for that part occurs. On the other hand, suppose that operation \(s\) of part \(i\) on machine \(j\) in cell \(k\) is processed. If operation \(s + 1\) for the same part on the other machines in the same cell \(k\) is processed, an intra-cell movement happens. In this study, several alternative routes are considered for processing of parts. In each route, several operations based on the sequence of operations are performed. The number of inter- and intra-cell movements for each part is also dependent on the sequence of operations. The machines’ reliability is calculated based on mean time between two failures (MTBF) and this number is exclusive for each machine.

Mathematical model

Indices

\(i\) : Index for parts, \(i = 1,2, \ldots ,P\)

\(j\) : Index for machines, \(j = 1,2, \ldots ,M\)

\(k\) : Index for cells, \(k = 1,2, \ldots ,C\)

\(r\) : Index for processing routes for part \(i,\) \(r = 1,2, \ldots ,R_{i}\)

\(s\) : Index for operations of part \(i\) in route \(r,\) \(s = 1,2, \ldots ,S_{ri}\)

\(t\) : Index for tool, \(t = 1,2, \ldots ,T\)

Parameters

\(C_{1i}\): Unit cost of parts movement between cells for part; \(i\); \(C_{2i}\): Unit cost of parts movement within cells for part; \(i\); \(C_{{jtt^{'} }}\): Unit cost of changing the tool \(t\) to \(t^{\prime}\) on machine \(j\)

\(\alpha_{ri}\) : cost of selection of route \(r\) for part \(i\)

\(\lambda_{sirjt}\) : processing time for operation \(s\) of part \(i\) in route \(r\) on the machine \(j\) by tool \(t\)

\(D_{i}\) : Demand for part \(i\)

\(L_{k}\) : Lower bound for number of machines in cell \(k\)

\(U_{k}\) : Upper bound for number of machines in cell \(k\); \(V_{t}\) : Maximum number of available tool \(t\); \(a_{sirjt}\) : 1 if operation \(s\) of part \(i\) in route \(r\) on machine \(j\) by tool \(t\) can be processed; 0 otherwise; \(MTBF_{j}\) : Mean time between two failures for machine \(j\); \(B_{j}\) : The failure cost for machine \(j\)

Decision variables

\(Z_{jk}\): 1 if machine \(j\) is assigned to cell \(k\); 0 otherwise \(X_{sirjkt}\) : 1 if operation \(s\) of part \(i\) in route \(r\) is processed on machine \(j\) in cell \(k\) by tool \(t\); 0 otherwise \(R_{ir}\) : 1 if route \(r\) is selected for part \(i\); 0 otherwise

Objective function

The objective function includes five cost terms: inter-cell, intra-cell, tool changing, machines’ failure, and routes’ selection costs. That is as follows:

$$\,Min\,z\, = \,\,\sum\limits_{i = 1}^{P} {\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{k = 1}^{C} {\sum\limits_{\begin{subarray}{l} k' = 1 \\ k \ne k^{\prime} \end{subarray} }^{C} {\sum\limits_{s = 1}^{{S_{ri} - 1}} {\sum\limits_{j = 1}^{M} {\sum\limits_{j' = 1}^{M} {\sum\limits_{t = 1}^{T} {\sum\limits_{{t^{\prime} = 1}}^{T} {C_{1i} } } } } } } } } } D_{i} X_{sirjkt} X_{{s + 1,irj^{\prime}k^{\prime}t^{\prime}}}$$
(1a)
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\sum\limits_{i = 1}^{P} {\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{k = 1}^{C} {\sum\limits_{\begin{subarray}{l} k' = 1 \\ k = k^{\prime} \end{subarray} }^{C} {\sum\limits_{s = 1}^{{S_{ri} - 1}} {\sum\limits_{j = 1}^{M} {\sum\limits_{\begin{subarray}{l} j' = 1 \\ j \ne j^{\prime} \end{subarray} }^{M} {\sum\limits_{t = 1}^{T} {\sum\limits_{{t^{\prime} = 1}}^{T} {C_{2i} } } } } } } } } } D_{i} X_{sirjkt} X_{{s + 1,irj^{\prime}k^{\prime}t^{\prime}}}$$
(1b)
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \sum\limits_{s = 1}^{{S_{ri} - 1}} {\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{i = 1}^{P} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{C} {\sum\limits_{t = 1}^{T} {\sum\limits_{{t^{\prime} = 1}}^{T} {C_{{jtt^{\prime}}} } D_{i} X_{sirjkt} } } } } } } X_{{s + 1,irjkt^{\prime}}}$$
(1c)
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{C} {\sum\limits_{i = 1}^{P} {\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{s = 1}^{{S_{ri} }} {\sum\limits_{t = 1}^{T} {\frac{{X_{sirjkt} D_{i} \lambda_{sirjt} B_{j} }}{{{\text{MTBF}}_{j} }}} } } } } }$$
(1d)
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\,\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{i = 1}^{P} {\alpha_{ri} } } R_{ir} \,.$$
(1e)

In the above equations, the term (1a) states that the inter-cell costs and (1b) represents intra-cell costs. Term (1c) calculates tools’ changing cost and term (1d) is related to machine breakdown costs and term (1e) is formulated as costs of route selection. Costs \(C_{1i}\) and \(C_{2i}\) can be dependent on the distance among machines within and between cells. In addition, these costs can be dependent on moving method for transmitting the parts between machines and cells. For instance, the small-size parts may be transferred between the machines manually, while the other parts need to be transferred by lift truck or other equipment. With considering these facts, the decision makers should calculate these costs. The cost \(C_{{jtt^{'} }}\) can be dependent to spend manpower cost for changing the tools, costs of tools’ transportation, and cost of lost opportunity for production as tool changing. Moreover, machine failure cost \(B_{j}\) for each machine \(j\) can be included fixed and variable cost of repair in addition to the machine breakdown opportunity. The cells and machines’ formation is done by route selection. It is obvious that route selection cost is dependent on relocation and setup costs of machines.

Constraints

$$\sum\limits_{r = 1}^{{R_{i} }} {R_{ir} } = 1\quad \forall \,i$$
(2)
$$\,\sum\limits_{k = 1}^{C} {\sum\limits_{j = 1}^{M} {\sum\limits_{t = 1}^{T} {a_{sirjt} X_{sirjkt} = } } } \,R_{ir\,} \quad \forall \,s,i,r$$
(3)
$$\,X_{sirjkt} \le Z_{jk} \quad \forall \,s,i,r,j,k,t,$$
(4)
$$\,\sum\limits_{j = 1}^{M} {Z_{jk} \ge L_{k} } \quad \forall \,k$$
(5)
$$\,\sum\limits_{j = 1}^{M} {Z_{jk} \le U_{k} } \quad \forall \,k$$
(6)
$$\,\sum\limits_{k = 1}^{C} {Z_{jk} = 1} \quad \forall \,j$$
(7)
$$\,\sum\limits_{s = 1}^{{S_{ri} - 1}} {\sum\limits_{i = 1}^{P} {\sum\limits_{r = 1}^{{R_{i} }} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{C} {X_{sirjkt} \le V_{t} \quad \forall \,t} } } } }$$
(8)
$$\,\,X_{sirjkt} ,R_{ir} ,Z_{jk} \in \left\{ {0,1} \right\}\quad \forall \,s,i,r,j,k,t.$$
(9)

The constraint 2 ensures that each part belongs to exactly one processing route. Constraint 3 states that if route \(r\) is selected for part \(i\), then this part should be processed exactly on one machine and by one tool and within one cell. Constraint 4 defines that if machine \(j\) is assigned to cell \(k\), each operation of part \(i\) can be processed on machine \(j\) by tool \(t\) in route \(r\) in cell \(k\). Constraints 5 and 6 present the maximum and minimum bounds for the number of machines in each cell, respectively. Constraint 7 guarantees that each machine is assigned to only one cell and constraint 8 states that the number of used tools cannot be more than available tools, while constraint 9 determines kind of each decision variable in the proposed model.

Linearization

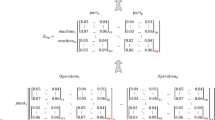
By considering three terms (1a), (1b), and (1c), the objective function is non-linear. However, these non-linear terms can be converted to linear ones by defining the new binary variables. In such condition, some further constraints should be added to the model. We can define two new binary variables as Eqs. 10 and 11 as follows:

$$\,\,W_{{sirjj^{\prime}kk^{\prime}tt^{\prime}}} = X_{sirjkt} X_{{s + 1,irj^{\prime}k^{\prime}t^{\prime}}} \quad \forall \,s,i,r,j,j^{\prime},k,k^{\prime},t,\,t^{\prime}$$
(10)
$$\,Q_{{sirjktt^{\prime}}} = X_{sirjkt} X_{{s + 1,irjkt^{\prime}}} \quad \forall \,s,i,r,j,k,t,\,t^{\prime}.$$
(11)

With respect to new variables, the further constraints like Eqs. 12–15 should be defined as follows:

$$X_{sirjkt} + X_{{s + 1,irj^{\prime}k^{\prime}t^{\prime}}} \le 1 + \,W_{{sirjj^{\prime}kk^{\prime}tt^{\prime}}} \quad \forall \,s,i,r,j,j^{\prime},k,k^{\prime},t,\,t^{\prime}$$
(12)
$$X_{sirjkt} + X_{{s + 1,irj^{\prime}k^{\prime}t^{\prime}}} \ge 2\,W_{{sirjj^{\prime}kk^{\prime}tt^{\prime}}} \quad \forall \,s,i,r,j,j^{\prime},k,k^{\prime},t,\,t^{\prime}$$
(13)
$$X_{sirjkt} + X_{{s + 1,irjkt^{\prime}}} \le 1 + \,Q_{{sirjktt^{\prime}}} \quad \forall \,s,i,r,j,k,t,\,t^{\prime}$$
(14)
$$X_{sirjkt} + X_{{s + 1,irjkt^{\prime}}} \ge 2\,Q_{{sirjktt^{\prime}}} \quad \forall \,s,i,r,j,k,t,\,t^{\prime}.$$
(15)

Numerical examples and validity of mathematical model

The GAMS software is known for integer linear and non-linear models. The most important features of this software are the high speed of model solving with many variables and construction. This capability helps which it be distinct in comparison to the other software. To validate the model and show its efficiency and performance, several numerical examples are generated and solved by branch and bound (B&B) method under SOLVER of linear programming called CPLEX in the GAMS software on a personal computer (Intel Core i5-3230 M 2.6 GHz and 6 GIG) under windows 8.

Solving the model in small-sized problem

An example including 4 parts, 4 machines, 8 processing routes (2 routes for each part), and 3 kinds of tools (5 units for each kind) is considered. Moreover, there are two cells with minimum and maximum capacities of 1 and 3, respectively. The required data for this example are given in Table 2. In this table, three initial columns are according to machine type, costs of machines’ breakdown, and MTBF, respectively. In addition, the part type, the demand for each part type, the alternative processing routes for each part type, and costs of route selection are represented in rows 1, 2, 3, and 4. The number of within the table in parentheses is operations processing time and out of parentheses is the sequence of operations and tool type used.

Table 2 Small-sized problem data
Full size table

For example, the number of 3–2(4) in intersection related to machine \(M_{3}\) and route \(R_{1}\) of part \(P_{1}\) is defined, so that “4 min is required for processing of the second operations of part type 1 in the first processing route on the machine type 3 by tool type 3”.

The data associated with inter-cell movement costs (\(C_{1i} )\), intra-cell movement costs (\(C_{2i}\)), and tool-changing costs on each machine type (\(C_{{jtt^{'} }}\)) are given in Table 3. In this example, four different relations between the above costs are considered. These relations are as follows:

Table 3 Small-sized problem data
Full size table
  1. 1.

    \(C_{1i}\), \(C_{2i}\), and \(C_{{jtt^{'} }}\) have not any relations

  2. 2.

    \(C_{1i} > C_{2i}\) and \(C_{{jtt^{'} }}\)

  3. 3.

    \(C_{2i} > C_{1i}\) and \(C_{{jtt^{'} }}\)

  4. 4.

    \(C_{{jtt^{'} }} > C_{1i}\) and \(C_{2i}\)

Computational results of small-sized problem

After solving the above problem by the proposed algorithm, the obtained results for \(X_{sirjkt}\), \(Z_{jk}\) and \(R_{ir}\) and related costs together with solving time considering the different states for \(C_{1i}\), \(C_{2i}\), and \(C_{{jtt^{'} }}\) are represented in Tables 4, 5, 6, and 7. The first row shows the part type. In addition, the second row indicates that the selected processing routes for each part and the last row, the obtained costs for five terms in the objective function, total cost, and solving time of the software are given. Moreover, the number of within parentheses is tool type and out of parentheses shows the sequence of operations.

Table 4 Results from GAMS for the small-sized problem/1
Full size table
Table 5 Results from GAMS for the small-sized problem/2
Full size table
Table 6 Results from GAMS for the small-sized problem/3
Full size table
Table 7 Results from GAMS for the small-sized problem/4
Full size table

Analysis of results for small-sized problem

From Table 4, it is deduced that machines 1, 3, and 4 are assigned to cell 1 and machine 2 to cell 2. In addition, the first processing route is selected for part type 1 and the second processing route for part types 2, 3, and 4. Besides, the mathematical model is so that as producing part type 4, inter- and intra-cell and tools’ changing occurs and all of the machines are used and there are not any idle machines.

As an example, the first process of part type 2 is performed on machine 2 in cell 2; while the second process of part type 2 occurs on machine 1 in cell 1, there is an inter-cell movement. On the other hand, the first process of part type 1 is performed on machine 1 in cell 1, while the second process of that part is performed on machine 3 from the same cell; thus, there is an intra-cell movement. The second process of part type 4 is produced on machine 1 in cell 1 by tool 3 and the third process of that part is produced on the same machine and in the same cell but by tool 2, and as a result, a tool changing occurs for part type 4. With respect to Table 5, the inter-cell movement in Table 6, and intra-cell movement in Table 7, the tool changing is not performed. Furthermore, the cost resulting movements and tool changing in the objective function are equal to zero. It should be noted that machine 4 is idle in states 2 and 3 (\(C_{1i} > C_{2i}\) and \(C_{{jtt^{'} }}\); \(C_{2i} > C_{1i}\) and \(C_{{jtt^{'} }}\)).

In the above example, a small-sized problem is designed and solved for several states and the analysis of the problem is showed model accuracy and performance. A large-sized problem is developed as follows.

Solving the model in large-sized problem

A shop decides to produce 6 part types on the 6 machine types by 3 tool types (number of 20 for each tool type). The engineering unit in shop suggests 3 processing routes for each part type. With respect to designing of the shop, 2 cells with capacities minimum and maximum 2 and 4, respectively. Table 8 includes data associated with the large-sized example. Table 9 also consists of inter-cell, intra-cell, and tools’ changing costs obtained by accounting unit located in the shop. Now, the manager of the production unit wants to know that what operations in which processing routes on which machines in which cells and by which tool should be processed. The outputs are the selected processing routes and cell formation, so that all of the demands are met. In addition, the incurred cost to shop for reaching the plan should be determined (notably, the descriptions related to data in the next tables are similar to the previous tables).

Table 8 Large-sized problem data
Full size table
Table 9 Large-sized problem data
Full size table

Computational results of large-sized problem

After solving the mathematical model proposed in this research, the obtained results are given in Table 10.

Table 10 Results from GAMS for the large -sized problem
Full size table

Analysis of results for large-sized problem

As it is seen in Table 10, machines 1, 3, and 5 are allocated to cell 1 and machines 2, 4, and 6 are assigned to cell 2. Machine 4 is idle over the planning horizon. The processing route 2 for part type 1 and processing route 3 is selected for the rest of part types. In addition, inter- and intra-cell movement and tool changing are as follows:

  • Part types 1 and 5: these two part types are transmitted only within one cell on the various machines.

  • Part type 2: machine 3 performs all of the processes of this part by several tools.

  • Part type 3: processes of this part are produced in one cell with an intra-cell movement and a tool changing.

  • Part type 4: this part needs only machine 1 with twice tool changing on it.

  • Part type 5: this part requires only to machines within one cell.

  • Part type 6: this part has one inter-cell movement and only one to change.

With solving of two examples, the proposed model is pursuing the optimal solutions among all solutions. In the other terms, for states that cost of movement is higher than tool-changing cost, although a part can have the inter- and/or intra-cell movements, the model tries to find a solution which part is allocated to one cell and with changing the tools, and processes of that part are completed. On the other hand, for states that cost of tool-changing cost is higher than movement costs, model decides to move the parts between or within different cells. Notably, because solving procedure used is able to solve even large-sized problems in a reasonable computational time thus, using the approximate methods is not required.

Conclusion

In this paper, an efficient model for CFP was developed with taking into account several important factors. Based on our knowledge, there is no similar research which considered inter- and intra-cell movement, tools’ changing, and route selection with respect to alternative routes, tools’ allocation, and machines’ reliability simultaneously. The tools’ allocation and tools’ changing capability on the machines are contributions of paper that they can prevent from further inter- and intra-cell movements. It means that with one or more tool changing on the one machine, the subsequent operations which may be required to other cells can be processed by one machine in one cell with changing of tools on that machine. To prevent the movement, some parts are necessary because of high cost and this results in using the tool-changing policy. Furthermore, it was observed that when different part types have more than one processing route, the cost of selected route and sum of breakdown costs for used machines in each of routes play an important role in selecting the processing route for each part.

Future researchers

In this research, the number of demand of parts, cells, machines, and available tools are deterministic and fixed in advanced. Each of these parameters can be considered uncertain for future researchers. Moreover, the number of machines for each type was considered equal to one. As a result, more than one machine can be challenging for this proposed model. Using the other solving method to solve with less computational time like heuristics and meta-heuristics can be an open study for the future. In addition, on machine tools’ replacement, this study suggests those conditions that could be considered in another way for future researchers.