Introduction

Forecasting is the process of making projections about future performance based on existing historic data. An accurate estimate aids in policy making and planning for the future. There are several motivations for trying to estimate the behavior of stock market prices. The most basic of these is financial gain. From the beginning of time, it has been man’s common goal to make his life easier. The prevailing notion in society is that wealth brings comfort and luxury, so it is not surprising that there has been so much work done on ways to predict the behavior of markets (Singh and Borah 2014; Vella and Ng 2014; Anbalagan and Maheswari 2015; Chen and Chen 2015; Dash et al. 2015; Sun et al. 2015; Rafiei et al. 2014). Any system that can consistently pick winners and losers in the dynamic market place would make the owner of the system very wealthy. Thus, many individuals including researchers, investment professionals, and average investors are continually looking for this superior system which will yield them high returns. In predicting stock value fluctuations, two hypotheses have emerged (Asadi et al. 2012; Aryanezhad et al. 2012; Jahromi et al. 2012):

  1. 1.

    It has been proposed in the Efficient Market Hypothesis (EMH) that markets are efficient in that opportunities for profit are discovered so quickly that they cease to be opportunities. The EMH effectively states that no system can continually beat the market because if this system becomes public, everyone will use it, thus negating its potential gain. Despite its rather strong statement that appears to be untrue in practice, there has been inconclusive evidence in rejecting the EMH. Different studies have concluded to accept or reject the EMH.

  2. 2.

    Prices always fully reflect the available information and, therefore, the past values of the time series summarize all the relevant information. In particular, the prices are determined by previous values in the time series and some researchers attempted to use artificial intelligent to validate their claims.

There has been no consensus on the EMH’s validity; therefore, various methods have been proposed and used for stock price forecasting with varying results. To reach this goal, two approaches can be employed: statistical and artificial intelligence (AI). The statistics approach includes autoregressive integrated moving average (ARIMA), generalized autoregressive conditional heteroskedasticity (GARCH) volatility and smooth transition autoregressive (STAR) (Sarantis 2001). These models depend on the assumption of linearity among variables and normal distribution. However, the assumption of linearity and normal distribution may not hold, even though it has been shown successful in dealing with stock price movement in the past decades. On the other hand, with greater in the stock market and the increasing need for more efficient forecasting models, the AI, operating without the limitation of such an assumption, outperforms the conventional statistical methods experimentally (Chen and Chen 2015; Dash et al. 2015; Ferreira et al. 2008; Jasemi and Kimiagari 2012). Artificial intelligence techniques such as artificial neural networks (ANNs), fuzzy logic, and genetic algorithms (GAs) are popular research subjects, since they can deal with complex engineering problems which are difficult to solve by classical methods. These techniques have been successfully used in the place of the complex mathematical systems for forecasting of time series (Singh and Borah 2014; Hadavandi et al. 2010; Shahrabi et al. 2013; Niaki and Hoseinzade 2013).

One of the major developments in AI over the last decade is the model combining or ensemble modeling. The basic idea of this multi-model approach is the use of each component model’s unique capability to better capture different patterns in the data. Both theoretical and empirical findings have suggested that combining different models can be an effective way to improve the predictive performance of each individual model (Mousavi et al. 2014; Hwang and Oh 2010; Alizadeh et al. 2011; Shen et al. 2011; Kar et al. 2015).

Baba et al. (2000) applied NNs and GAs to design an intelligent decision support system (DSS) for analyzing the Tokyo Stock Exchange Prices Indexes (TOPIX). The necessary feature of their DSS was that it projected the high and low TOPIX values 4 weeks into the future and proposed buy and sell decisions based on the average projected value and the then-current value of the TOPIX.

Su and Hsu (2005) proposed new method with two-stage architecture for improved stock price prediction. The self-organizing map (SOM) clustering at first used to decompose the whole input space into regions where data points with similar statistical distributions are grouped together. After decomposing heterogeneous data points into several homogenous regions, support vector regression (SVR) is applied to predict financial indices. The suggested technique is empirically tested by stock price series from seven markets. The results indicate that the performance of stock price prediction can be enhanced using the two-stage architecture in comparison with a single SVR model.

Chang and Liu (2008) for stock price prediction used a Takagi–Sugeno–Kang (TSK) type fuzzy rule-based system (FRBS). They used simulated annealing (SA) for tuning the best parameters of fuzzy systems. They detected that the forecasted results from TSK fuzzy rule based model were better than back propagation network (BPN) or multiple regressions.

Esfahanipour and Aghamiri (2010) used Adaptive neuro Fuzzy Inference System (ANFIS) for stock price forecasting. The TSK fuzzy model uses the technical index as the input variables. Results indicated that their model has better performance and effectively improved the forecasting accuracy of other models.

Fuzzy expert systems (FES) have demonstrated their superb ability as system identification tools. FES processes knowledge sequentially and formulates it into rules. They can be used to formulate trading rules based on input variable (Asadi and Shahrabi 2016a, b). The advantage of FES is that they can explain how they derive their results. With neural networks, it is difficult to analyze the importance of input data and how the network derived its results. The major problem with applying FES to the stock market is the difficultly in formulating knowledge of the markets, because we ourselves do not completely understand them. In a highly chaotic and only partially understood environment, such as the stock market, this is an important factor. It is hard to extract information from experts and formalize it in a way usable by FES (Trawiński et al. 2012, 2013). Hence in recent years, it is based on evolutionary algorithms to automatically extract fuzzy expert system by identifying and estimating the fuzzy rule base while keeping a generic structure. In fact, the automatic definition of fuzzy systems can be considered as an optimization or search process and nowadays, evolutionary algorithms, particularly genetic algorithm, are considered as the more known and used global search technique. Genetic algorithm has been successfully applied to learn fuzzy systems in the last years, giving a way to the appearance of the so-called genetic fuzzy systems (GFS). GFS offers a better way to represent complicated situations and has been applied very practically in many fields where classical models are difficult to implement for the design and learning (Trawiński et al. 2013; Herrera 2008; De et al. 2015).

Hadavandi et al. (2010) presented an integrated approach based on genetic fuzzy systems (GFS) and artificial neural networks for constructing a stock price prediction expert system. They used stepwise regression analysis to determine factors which have most influence on stock prices, then divided the raw data into k clusters by means of self-organizing map (SOM) neural networks. Finally, all clusters fed into independent GFS models with the ability of rule base extraction and data base tuning. Results for IBM stock price showed that their approach outperforms other methods such as ANN and ARIMA.

Data mining is the process of extracting useful information from data sets by incorporating tools and techniques. In time series forecasting, using data mining for preprocessing impacts forecasting performance. Some of the data preprocessing stages are used to choose the key variables, make our raw data clean, reduce the complexity of the whole data space to something more homogeneous and also reduce the effects of noisy data (Asadi et al. 2012, 2013).

However, in drawing conclusions, FES approaches are considered as good tools to assist; as a matter of fact, the accuracy is extremely dependent on the suitable feature of input parameters. On the other hand, one of the problems associated with this kind of modeling is that the accuracy and the interpretability of the obtained model are contradictory properties directly depending on the learning process and/or the model structure (Alcala-Fdez et al. 2011; Galar et al. 2011). Furthermore, in complex multidimensional problems with highly nonlinear input–output relations, many redundant, inconsistent, and conflicting rules are usually found in the obtained rule base; on the other hand, the number of rules goes up exponentially with the number of input variables; this drawback is called the “curse of dimensionality,” which is detrimental to the linguistic fuzzy model performance and interpretability. In any case, these rules could not cooperate appropriately and dramatically affect the performance of the model (Trawiński et al. 2012, 2013). A number of studies in the literature have discussed “curse of dimensionality” and proposed a variety of FES structures. The conventional FES is proved to be a very promising tool for dealing with forecasting (Herrera 2008).

Extracting high-quality rules and coordinating them to establish teamwork are among the most challenging issues in the existing literature on the rule learning problem. In this paper, firstly, the best rules are learned using an evolutionary approach. Next, a binary GA is used to identify redundant rules. In this stage, a fuzzy system of high-quality rules is already formed which contains no redundancy. Finally, to coordinate the rules and enhance teamwork, a GA is employed and the rule base of the fuzzy system is tuned.

This paper presents a hybrid artificial intelligence model to develop a Mamdani type fuzzy rule-based system with approximate rules. The hybrid model uses data mining to improve accuracy and uses genetic algorithm and evolutionary strategy to evolve the knowledge base of FES (DEFES). We evaluate the capability of the proposed approach by applying it to the forecasting case studies of International Business Machines Corporation (IBM) stock price, and compare the outcomes and the results of the other methods with MAPE metric and Wilcoxon signed ranks test.

Case studies of International Business Machines Corporation (IBM) have been used in different studies to test forecasting accuracy of different approaches. Hassan and Nath (2005) proposed a Hidden Markov Model (HMM) to generate 1-day forecasts of stock prices in a novel way. Hassan et al. (2007) proposed and developed a fusion model combining the HMM with an Artificial Neural Network and a Genetic Algorithm to achieve better forecasts. In their model, ANN was used to transform the input observation sequences of HMM and the GA was used to optimize the initial parameters of the HMM. Hassan (2009) proposed a novel combination of the HMM and the fuzzy models for forecasting stock market data. The model used HMM to identify data patterns and then used fuzzy logic to generate appropriate fuzzy rules and obtain a forecast value for next day stock price. The forecast accuracy of the combination HMM–fuzzy model was better when compared to the ARIMA and ANN and other HMM-based forecasting models. Moreover, he performed a comparison of profit for the proposed models for the mentioned stocks that the transaction decision was made based on forecasting of the stock price. He concluded that the method which has the lowest MAPE value gains much more profit.

The remainder of the paper is organized as follows: In “Data mining-based evolutionary fuzzy expert system (DEFES)”, the methodology is presented. This section gives a brief description on the theory and discusses the proposed approach (DEFES). In “Application of the DEFES”, DEFES is applied to financial markets forecasting and its performance is compared with those of other models. The paper ends with proper conclusions.

Data mining-based evolutionary fuzzy expert system (DEFES)

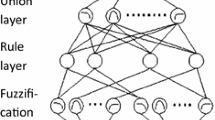
General framework of DEFES is shown in Fig. 1. DEFES consists of two main procedures:

Fig. 1
figure 1

DEFES structure

Full size image
Fig. 2
figure 2

Encoded chromosome for extraction of approximate Mamdani type fuzzy rule-based system

Full size image

Data mining: In stages 1, 2 and 3, noise filtering, SRA and clustering are used to reduce the complexity of the whole data space.

Constructing FES: In stage 3, 4 and 5 the knowledge base (KB) of the FES for each subpopulation is extracted by means of genetic algorithm and evolutionary strategy.

At the stage 7, tuning of parameter’s model, it has tested efficiency of the model. In the following, we will describe each stage.

Data mining: noise filtering by Savitzky–Golay smoothing filter

Data quality is a key issue with forecasting concepts. To increase the accuracy of the forecasts, we may perform data mining techniques, otherwise, garbage in may lead to garbage out. Data cleaning is one of the most important steps of data mining, because real-world data are naturally noisy, incomplete and inconsistent. In this study, we apply one of the well-adapted noise filtering techniques which is called Savitzky–Golay smoothing filter (SGF) (Angrisani et al. 2014) to clean and smooth out our noisy data and prepare more appropriate data to be fed into our AI model. The smoothing process attempts to estimate the average of the distribution of each response value. The estimation is based on a specified number of neighboring response values. We may consider smoothing as a local fit because a new response value is created for each original response value.

Recall that a digital filter is applied to a series of equally spaced data values \(f_{i} \equiv f(t_{i} )\), where \(t_{i} \equiv t_{0} + i\Delta\) for some constant sample spacing Δ and \(i = . . . - 2, - 1, 0, 1, 2, \ldots\). Simplest type of digital filter replaces each data value f i by a linear combination gi of itself and some number of nearby neighbors:

$$g_{i} = \mathop \sum \limits_{{k = - n_{\text{L}} }}^{{n_{\text{R}} }} c_{n} f_{i + n}$$
(1)

Here, n L is the number of points used “to the left” of a data point i, i.e., earlier than it, while n R is the number used to the right, i.e., later. A so-called causal filter would have \(n_{\text{R}}\). The idea of Savitzky–Golay filtering is to find filter coefficients c n that preserve higher moments. Equivalently, the idea is to approximate the underlying function within the moving window not by a constant, but by a polynomial of higher order, typically quadratic or quartic: For each point \(f_{i}\), we least-squares fit a polynomial to all \(n_{\text{L}} + n_{\text{R}} + 1\) points in the moving window, and then set g i to be the value of that polynomial at position i. We make no use of the value of the polynomial at any other point. When we move onto the next point f i  + 1, we do a whole new least-squares fit using a shifted window. All these least-squares fits would be laborious if done as described. Luckily, since the process of least-squares fitting involves only a linear matrix inversion, the coefficients of a fitted polynomial are themselves linear in the values of the data. That means that we can do all the fitting in advance, for fictitious data consisting of all zeros except for a single 1, and then do the fits on the real data just by taking linear combinations. This is the key point, then: there are particular sets of filter coefficients \(c_{n}\), for which Eq. (1) “automatically” accomplishes the process of polynomial least-squares fitting inside a moving window.

To derive such coefficients, consider how g 0 might be obtained: we want to fit a polynomial of degree M in \(i\), namely \(a _{0} + a _{1} i + \cdots + a _{M} i^{M}\) to the values \(f_{{ - n{\text{L}}}} , . . . , f_{{n{\text{R}}}}\). Then, g 0 will be the value of that polynomial at \(i = 0\), namely \(a_{0}\). The design matrix for this problem is:

$$A_{ij} = i^{j} , i = - n_{\text{L}} \ldots n_{\text{R}} , \;j = 0, \ldots ,M$$
(2)

and the normal equations for the vector of a j ’s in terms of the vector of \(f_{i}\)’s are in matrix notation

$$(A^{\text{T}} .A).a = A^{\text{T}} .f \; {\text{or}} \; a = (A^{\text{T}} .A)^{ - 1} .(A^{\text{T}} .f)$$
(3)

We also have the specific forms:

$$\left\{ {A^{\text{T}} .A} \right\}_{ij} = \mathop \sum \limits_{{k = - n_{\text{L}} }}^{{n_{\text{R}} }} A_{ki} .A_{kj} = \mathop \sum \limits_{{k = - n_{\text{L}} }}^{{n_{\text{R}} }} k^{i + j} (14.8.4)$$
(4)
$$\left\{ {A^{\text{T}} .f} \right\}_{j} = \mathop \sum \limits_{{k = - n_{\text{L}} }}^{{n_{\text{R}} }} A_{ki} f_{k} = \mathop \sum \limits_{{k = - n_{\text{L}} }}^{{n_{\text{R}} }} k^{i} f_{k} (14.8.4)$$
(5)

Since the coefficient c n is the component a 0 when f is replaced by the unit vector e n ,

\(- n_{\text{L}} \le n \le n_{\text{R}}\), we have:

$$c_{n} = \left\{ {(A^{\text{T}} .A)^{ - 1} .(A^{\text{T}} .e_{n} )} \right\}_{0} = \mathop \sum \limits_{m = 0}^{M} \left\{ {(A^{\text{T}} .A)^{ - 1} } \right\}_{0m} n^{m}$$
(6)

Note that Eq. (6) says that we need only one row of the inverse matrix. (Numerically, we can get this by LU decomposition with only a single backsubstitution.)

Data mining: variables selection by stepwise regression analysis

Variable selection is the process of selecting an optimum subset of input variables from the set of potentially useful variables which may be available in a given problem. Different researchers have applied variety of feature selection methods, such as genetic algorithm (El Alami 2009), principal component analysis (Zhang and Zhang 2002) and stepwise regression analysis (SRA) to select the key factors in their forecasting systems. Among them, in recent years some researcher have used SRA for input variable selection in the field of stock market forecasting and they have obtained very promising results (Chang and Liu 2008). So, in this paper we adopt stepwise regression to analyze and select the variables and, as its consequence, to improve the forecasting accuracy of the system. Stepwise regression method determines the set of factors that most closely determine the dependent variable. This task is carried out by means of the repetition of a variable selection.

To illustrate the procedure (as described in Niknam and Amiri 2010), assume that we have K candidate variables \(x_{1} ,x_{2} , \ldots ,x_{k }\) and a single response variable y. In classification, the candidate variables correspond to the polynomial-expanded elements of the feature vectors and the response variable corresponds to the class label. Note that with the intercept term β 0 we end up with \(K + 1\) variables. In the procedure, the polynomial weights (or the regression model) are iteratively found by adding or removing variables at each step. The procedure starts by building a one variable regression model using the variable that has the highest correlation with the response variable y. This variable will also generate the largest partial F-statistic. In the second step, the remaining K − 1 variables are examined. The variable that generates the maximum partial F-statistic is added to the model provided that the partial F-statistic is larger than the value of the F-random variable for adding a variable to the model, such an F-random variable is referred to as f in. Formally, the partial F-statistic for the second variable is computed by:

$$f_{2} = \frac{{{\text{SS}}_{\text{R}} (\beta_{2} |\beta_{1} ,\beta_{0} )}}{{{\text{MS}}_{\text{E}} (x_{2} ,x_{1} )}}$$
(7)

where MSE (x 2, x 1) denotes the mean square error for the model containing both \(x_{1}\) and \(x_{2}\). SSR(β 2|β 1, β 0) is the regression sum of squares due to β 2 given that β 1, β 0 are already in the model. In general, the partial F-statistic for variable j is computed by:

$$f_{j} = \frac{{{\text{SS}}_{\text{R}} (\beta_{j} |\beta_{0} ,\beta_{1} , \ldots ,\beta_{j - 1} ,\beta_{j + 1} , \ldots ,\beta_{k} )}}{{{\text{MS}}_{\text{E}} }}$$
(8)

If variable x 2 is added to the model, then the procedure determines whether the variable x 1 should be removed. This is determined by computing the F-statistic:

$$f_{1} = \frac{{{\text{SS}}_{\text{R}} (\beta_{2} |\beta_{1} ,\beta_{0} )}}{{{\text{MS}}_{\text{E}} (x_{2} ,x_{2} )}}$$
(9)

If f 1 is less than the value of the F-random variable for removing variables from the model, such an F-random variable is referred to as f out. The procedure examines the remaining variables and stops when no other variable can be added or removed from the model. It is also worth mentioning that one cannot arrive to the conclusion that all of the regressors that are important for predicting the response variable have been retained in the stepwise procedure. This is so because such a procedure retains regressors based on the use of sample estimates of the true model weights.

Data mining: data clustering by K-means

Clustering algorithms are classified into two groups: the agglomerative hierarchical algorithms such as the centroid and Ward methods, and the nonhierarchical clustering (de Oliveira and Pedrycz 2007), such as K-means and SOM neural networks. Each of these algorithms has their own advantages and disadvantages. Depending on the application, a particular type of clustering method should be chosen. Among clustering algorithms, because of simplicity and fast convergence of K-means, it has been used in a wide range of applications (Yiakopoulos et al. 2011).

The K-means method (Niknam and Amiri 2010) is a technique employed for partitioning a set of objects into k groups such that each group is homogeneous with respect to certain attributes based on the specific criterion. We use K-means data clustering to divide the data into sub-populations and reduce complexity of the whole data space, decompose complicated patterns to a set of simple patterns and decrease effects of noise by focusing on similar data in each cluster and consequently have higher accuracy.

Given a set of observations(x 1, x 2, …, x n ), where each observation is a dimensional real vector then K-means clustering aims to partition the observations into sets (k < n), the procedure of K-means method is summarized below:

Step 1: Randomly select k initial cluster centroids, where k is the number of the clusters.

Step 2: Assigned each object to the cluster to which it is the closest based on the distance between the object and the cluster mean (we use Euclidean metric as the distance function).

$$d(x_{i} ,m_{i} ) = x_{i} - m_{i} = \sqrt {\mathop \sum \limits_{k = 1}^{d} (x_{ik} - m_{jk} )^{2} }$$
(10)

where \(x_{i}\) is the ith observation, m j is the centroid of the jth cluster and is the dimension of input vectors.

Step 3: Calculate the new mean for each cluster and reassign each object to the cluster.

Step 4: Stop if the criterion converges (the algorithm is deemed to have converged when the assignments no longer change). Otherwise go back to Step 2.

Extraction of approximate Mamdani type fuzzy rule-based system

In a very broad sense, an FES can be used as the basis for the representation of different forms of system knowledge, or to model the interactions and relationships among the system variables. FESs have proven to be an important tool for modeling complex systems, in which, due to the complexity or the imprecision, classical tools are unsuccessful. In this sense, a large amount of methods have been proposed to automatically generate fuzzy rules from numerical data. Usually, they use complex rule generation mechanisms such as neural networks or genetic algorithms. Recently, a great number of publications explore the use of Genetic Algorithms (GAs) for designing fuzzy expert systems. These approaches receive the general name of Genetic Fuzzy Systems (GFSs). The automatic definition of an FES can be considered in many cases as an optimization or search process (Trawiński et al. 2013; Herrera 2008). GAs is the best known and most widely used global search technique with an ability to explore and exploit a given operating space using available performance measures (Asadi et al. 2012, 2013; Shahrabi et al. 2013; Razavi et al. 2015). GAs is known to be capable of finding near optimal solutions in complex search spaces. A prior knowledge may be in the form of linguistic variables, fuzzy membership function parameters, fuzzy rules, number of rules, etc. The generic code structure and independent performance features of GAs make them suitable candidates for incorporating a priori knowledge. These advantages have extended the use of GAs in the development of a wide range of approaches for designing fuzzy expert systems over the last few years. As is well known, the Knowledge Base (KB) of an FES is composed of two components, a Data Base (DB), containing the definitions of the scaling factors and the membership functions of the fuzzy sets specifying the meaning of the linguistic terms, and a Rule Base (RB), constituted by the collection of fuzzy rules. GAs may be applied to adapting/learning the DB and/or the RB of an FRBS (Ishibuchi et al. 2005).

The shape of membership functions is based on two variants, depending on the fuzzy model, whether approximate (Herrera 2008) or descriptive (Cordón et al. 2001). The descriptive fuzzy model is essentially a qualitative expression of the system. A KB in which the fuzzy sets giving meaning (semantic) to the linguistic labels is uniformly defined for all rules included in the RB. It constitutes a descriptive approach since the linguistic labels take the same meaning for all the fuzzy rules contained in the RB. The system uses a global semantics. In the approximate fuzzy model, a KB is considered for which each fuzzy rule presents its own meaning, i.e., the linguistic variables involved in the rules do not take as their values any linguistic label from a global term set. In this case, the linguistic variables become fuzzy variables. The approximate fuzzy model is more precise than descriptive fuzzy model; therefore, in this paper it is used approximate fuzzy model (Cordón and Herrera 2001).

In this paper, it is used a Mamdani type fuzzy rule-based system (FRBS) for simulation behavior stock price. In a Mamdani type FRBS, a common rule is represented as follows:

\({\text{if}} \;X_{1} \; {\text{is}}\; A_{i} \; {\text{and }}\;X_{2} \; {\text{is}}\; A_{i} \; {\text{THEN}} \;Y \;{\text{is}}\; B_{i},\) where \(X_{1}\),\(X_{2}\) and Y are linguistic variables and \(A_{i}\), \(B_{i}\) and are corresponding fuzzy sets. In the following, we will describe evolutionary process that we use in this paper for evolving knowledge base of FRBS. In this study, we use a novel genetic fuzzy system (GFS) type based on a method proposed by Cordon and Herrera (2001) to extracting the whole KB of Mamdani type fuzzy rule-based system for each sub-population and construct expert system with the ability of simulating behavior of stock price. The expert system extraction process can be decomposed in six steps that have shown in Fig. 3. In the following, we will discuss these steps.

Fig. 3
figure 3

Extraction of approximate Mamdani type fuzzy rule-based system

Full size image

Step 1: Coding

In the proposed model, a previously defined DB constituted by uniform fuzzy partitions with triangular membership functions crossing at height 0.5 is considered. The number of linguistic terms forming each of them can be specified by the designer. A chromosome C encoding a candidate rule is composed of two different parts, C 1 and C 2, each one corresponding to each one of the fuzzy rule base components. The first part of the chromosome encodes the composition of the fuzzy rule and the second one the membership functions involved in it. To represent the first part, there is a need to number the primary fuzzy sets belonging to each one of the variable fuzzy partitions considered. A fuzzy variable x i taking values in a primary set \(T(x_{i} ) = \{ L_{1} (x_{1} ),L_{2} (x_{2} ), \ldots ,L_{ni} (x_{{n_{i} }} )\}\) has associated the ordered set \(T^{'} (x_{i} ) = \left\{ {1,2, \ldots ,n_{i} } \right\}\). On the other hand, the second part is based on triangular membership functions composing the rule; L i (x i ) is encoded by means of its associated 3-tuple \(\{ a_{{L_{i} (x_{i} )}} ,b_{{L_{i} (x_{i} )}} ,c_{{L_{i} (x_{i} )}} \}\) that is shown in Fig. 2.

Step 2: Generating the initial population

A third of the initial gene pool is created making use of the training data set \(D_{\text{p}}\) and other third is initiated totally at random. The initialization of the individuals belonging to the remaining third takes common characteristics of the other two. The first part of them is initiated from the examples and the second one at random. With M being the GA population size and \(t = { \hbox{min} }\left\{ {D_{\text{p}} ,\frac{M}{3}} \right\}\), let t examples be selected at random from \(E_{\text{p}}\). Then, the initial population generation process is performed in three steps as follows (Fig. 3):

1. Making use of the existing linguistic variable primary fuzzy partitions, generate t individuals by taking the rule best covering each one of the t randomly obtained examples. Initiate C 1 and C 2 by coding, respectively, the rule primary fuzzy sets and their meaning in the said way.

2. Generate another t individual initiating C 1 in the same way that in the previous step, and computing the values of C 2 at random, each gene varying in its respective interval.

3. Generate the remaining \(M - 2 t\) individuals by computing at random the values of the first part, C 1, and making use of these for randomly generating the C 2 part, each gene varying in its respective interval.

Step 3: Fitness function

The fitness function measuring the adaptation of each rule of the population is a multiobjective function-based high three criteria: frequency value, high average covering degree over positive examples and high average covering degree over positive examples, shown in Fig. 4.

Fig. 4
figure 4

Fitness function for extraction of approximate Mamdani type fuzzy rule

Full size image
Fig. 5
figure 5

Fitness function for rule filtering and tuning KB

Full size image

Step 4: Genetic operator

Due to the special nature of the chromosomes involved in this generation process, the design of the genetic operators able to deal with it becomes a main task. As there exists a strong relationship between both chromosomes parts, operators working cooperatively in C 1 and C 2 are required to make the best use of the representation used. It can be clearly observed that the existing relationship will present several problems if not handled adequately. For example, modifications in the first chromosome part have to be automatically reflected in the second one. It makes no sense to modify the primary fuzzy set and continue working with the previous membership function. On the other hand, there is a need to develop the recombination in a correct way to obtain meaningful offsprings. Taking into account these aspects, the following operators are going to be considered:

Selection and elitism: The best 10 % of the population are copied without changes in the elitism set. Elitism set ensures that the best chromosomes will not be destroyed during crossover and mutation. The selection process is then implemented. We use binary tournament selection scheme to selecting chromosomes for mating pool. The size of the mating pool equals 90 % of the population size.

Crossover: With regard to the recombination process, two different crossover operators are employed depending on the two parents’ scope:

  1. a.

    Crossover when both parents encode the same rule:

If \(C_{v}^{t} = (c_{1} , \ldots ,c_{k} , \ldots ,c_{H} )\) and \(C_{w}^{t} = (c{\prime }_{ 1} , \ldots , c{\prime }_{k} , \ldots , c{\prime }_{H} )\) are to be crossed, the following four offsprings are generated:

$$C_{1}^{t + 1} = aC_{w}^{t} + (1 - a)C_{v}^{t}$$
$$C_{2}^{t + 1} = aC_{v}^{t} + (1 - a)C_{w}^{t}$$
$$C_{3}^{t + 1} \; {\text{with}} \;C_{3k}^{t + 1} = \hbox{min} \{ c_{k} ,c'_{k} \}$$
$$C_{4}^{t + 1} \;{\text{with}}\; C_{4k}^{t + 1} = \hbox{max} \{ c_{k} ,c'_{k} \}$$
(11)

This operator can use a parameter which is either a constant or a variable whose value depends on the age of the population. The resulting descendents are the two best of the four aforesaid offspring.

  1. b.

    Crossover when the parents encode different rules:

In this second case, it makes no sense to apply the previous operator because it will provoke the obtaining of disrupted descendents. This fact is because the combination of two membership functions associated with different primary fuzzy sets makes the obtaining of two new fuzzy sets not belonging to the intervals of performance determined by the initial fuzzy partition. A standard crossover operator is applied over both parts of the chromosomes. A crossover point c p is randomly generated in C 1 and the two parents are crossed at the c p th and \(n + 1 + 3. c_{\text{p}}\) genes.

$$C_{t} = (c_{1} , \ldots ,c_{p} ,c_{p + 1} , \ldots ,c_{n + 1} ,a_{{ c_{1} }} ,b_{{ c_{1} }} ,c_{{ c_{1} }} , \ldots ,a_{{ c_{p} }} ,b_{{ c_{p} }} ,c_{{ c_{p} }} ,a_{{ c_{p + 1} }} ,b_{{ c_{p + 1} }} ,c_{{ c_{p + 1} }} , \ldots ,a_{{ c_{n + 1} }} ,b_{{ c_{n + 1} }} ,c_{{ c_{n + 1} }} )$$
$$C^{\prime }_{t} = (c^{\prime }_{1} , \ldots ,c^{\prime }_{p} ,c^{\prime }_{p + 1} , \ldots ,c^{\prime }_{n + 1} ,a^{\prime }_{{ c^{\prime }_{1} }} ,b^{\prime }_{{ c^{\prime }_{1} }} ,c^{\prime }_{{ c^{\prime }_{1} }} , \ldots ,a^{\prime }_{{ c^{\prime }_{p} }} ,b^{\prime }_{{ c^{\prime }_{p} }} ,c^{\prime }_{{ c^{\prime }_{p} }} ,a^{\prime }_{{ c^{\prime }_{p + 1} }} ,b^{\prime }_{{ c^{\prime }_{p + 1} }} ,c^{\prime }_{{ c^{\prime }_{p + 1} }} , \ldots ,a^{\prime }_{{ c^{\prime }_{n + 1} }} ,b^{\prime }_{{ c^{\prime }_{n + 1} }} ,c^{\prime }_{{ c^{\prime }_{n + 1} }} )$$

the two resulting offsprings are:

$$C_{t + 1} = (c_{1} , \ldots ,c_{p} ,c'_{p + 1} , \ldots ,c'_{n + 1} ,a_{{ c_{1} }} ,b_{{ c_{1} }} ,c_{{ c_{1} }} , \ldots ,a_{{ c_{p} }} ,b_{{ c_{p} }} ,c_{{ c_{p} }} , \ldots ,a'_{{c_{p + 1}^{'} }} ,b'_{{c_{p + 1}^{'} }} ,c'_{{c_{p + 1}^{'} }} , \ldots ,a'_{{c_{n + 1}^{'} }} ,b'_{{c_{n + 1}^{'} }} ,c'_{{c_{n + 1}^{'} }} )$$
$$C'_{t + 1} = (c'_{1} , \ldots ,c'_{p} ,c_{p + 1} , \ldots ,c_{n + 1} ,a_{{c_{1}^{'} }}^{'} ,b_{{c_{1}^{'} }}^{'} ,c_{{c_{1}^{'} }}^{'} , \ldots ,a_{{c_{p}^{'} }}^{'} ,b_{{c_{p}^{'} }}^{'} ,c_{{c_{p}^{'} }}^{'} ,a_{{ c_{p + 1} }} ,b_{{ c_{p + 1} }} ,c_{{ c_{p + 1} }} , \ldots ,a_{{ c_{n + 1} }} ,b_{{ c_{n + 1} }} ,c_{{ c_{n + 1} }} )$$

Mutation: Mutation on C 2 is based on a real-coding scheme; Michalewicz’s non-uniform mutation operator is employed (Hassan et al. 2007). If \(C_{v}^{t} = \left( {c_{1} , \ldots ,c_{k} , \ldots ,c_{H} } \right)\) is a chromosome and the element c k was selected for this mutation (the domain of c k is [c kl ; c kr ]), the result is a vector \(C_{v}^{t} = \left( {c{\prime }_{1} , \ldots ,c{\prime }_{k} , \ldots ,c_{H} } \right)\) with k ∊ {1, …, H} and

$$c{\prime }_{k} = \left\{ {\begin{array}{*{20}c} {c_{k} + \Delta \left( {t,c_{kr} - c_{k} } \right) \quad {\text{if}}\,\, a = 0} \\ {c_{k} + \Delta \left( {t,c_{k} - c_{kl} } \right) \quad {\text{if}}\,\, a = 1} \\ \end{array} } \right.$$
(12)

where a is a random number that may have a value of zero or one, and the function \(\Delta (t,y)\) returns a value in the range [0, y] such that the probability of \(\Delta (t,y)\) being close to 0 increases as t increases:

$$\Delta (t,y) = y\left( {1 - r^{{\left( {1 - \frac{t}{T}} \right)^{b} }} } \right)$$
(13)

\(r\) is a random number in the interval \(\left[ {0 , 1} \right],\) T is the maximum number of generations and b is a parameter chosen by the user.

Evolution strategy (ES): ESs were at first developed by Rechenberg and Schwefel in 1964 with a powerful focus on building systems proficient of solving difficult real-valued parameter optimization problems (Cordón 2001; Cordón and Herrera 2001).

In this paper, each time a GA generation is performed; the ES will be applied over a percentage α of the best different population individuals existing in the current genetic population. This optimization technique has been selected and integrated into the genetic recombination process to perform a local tuning of the best population individuals in each generation. It allows us to improve again a strong exploitation over the promising space zones found in each generation by adjusting the C 2 part values of the chromosomes located at them. Now we are going to describe the adaptation of this algorithm to our problem.

In the (1 + 1) − ES, the mutation strength relies directly on the value of the parameter \(\sigma\), which determines the standard deviation of the normally distributed random variable \(z_{i}\). In our case, the step size σ cannot be a single value because each one of the membership functions encoded in the second part of the chromosome is defined over different universes and so requires different order mutations. Therefore, a step size σ i  = σ × s i for each component has already been used in the (1 + 1) − ES. Anyway, the relations of all σ i were fixed by the values s i and only the common factor σ is adapted. In our problem, each of the three correlative parameters (x 1, x 2, x 3) defines a triangular-shaped membership function and the property \(x_{1} \le x_{2} \le x_{3}\) must be confirmed to obtain significant fuzzy sets.

With C i  = (x 0, x 1, x 2) being the membership function currently adapted, the associated interval of performance is \(\left[ {C_{i}^{\text{l}} ,C_{i}^{\text{r}} } \right] = \left[ {x_{0} - \frac{{x_{1} - x_{0} }}{2},x_{2} - \frac{{x_{2} - x_{1} }}{2}} \right]\). The adaptation is based on generating the mutated fuzzy set C ’ i  = (x ′0 , x ′1 , x ′2 ) by first adapting the modal point x 1 obtaining the mutated value x ′1 and then adopt x 0, x 2, respectively, in Fig. 6:

Fig. 6
figure 6

Adapting membership function with ES

Full size image

Step 5: Covering value

The covering method is developed as an iterative process that allows us to obtain a set of fuzzy rules covering the example set. In each iteration, it runs the generating method, obtaining the best fuzzy rule according to the current state of the training set, considers the relative covering value this rule provokes over it, and removes from it the examples with a covering value greater than \(\varepsilon\). The covering value of an example e l  ∊ E l s is defined as:

$${\text{CV}}_{\text{R}} (e_{l} ) = \mathop \sum \limits_{l = 1}^{p} R_{i} (e_{l} )$$
(14)

Rule filtering

Due to the iterative nature of the genetic generation process, an overlearning phenomenon may appear. This occurs when some examples are covered at the high degree (an instance covered by several rules). To solve this problem and improve its accuracy, it is necessary to simplify the rule set obtained from the previous stage to deriving final RB. The simplification process is designed as follows:

Step 1: Coding

It is based on a binary-coded GA. Considering the rules contained in the rule set B g derived from the previous stage counted from 1 to m, an m bit string C = (c 1, c 2, …, c m ) represents a subset of candidate rules to form the RB finally obtained as this stage; it is shown in Fig. 7. If c i s one indicates that i rule is active in this RB, otherwise it is nonnative.

Fig. 7
figure 7

Encoded chromosome rule filtering

Full size image

Step 2: Generating the initial population

The initial population is generated by introducing a chromosome representing the complete previously obtained rule set B g that is, with all c i  = the remaining chromosomes are selected at random.

Step 3: Fitness function

It is based on an application-specific measure usually employed in the design of GFSs, the mean square error (MSE) over a training data set and training set completeness degree of R(C j ) which is shown in Fig. 5.

Step 4: Genetic operator

Selection of the individuals is developed using the stochastic universal sampling procedure together with an elitist selection scheme and the generation of the offspring population is put into effect using the classical binary multipoint crossover (performed at two points) and uniform mutation operators.

Genetic tuning process

After generation of rule base, this tuning process slightly adjusts the shape of the membership functions of a preliminary DB defined. This approach can be decomposed in the following steps:

Step 1: Coding

The GA designed for tuning process presents a real-coding issue. Taking into account the parametric representation of the triangular-shaped membership functions based on a 3-tuple of real values, each one of the rules is encoded in pieces of the chromosome \(C_{i}^{j} ,i = 1, \ldots ,n = m + 1\) in the following way:

$$C_{i}^{j} = (a_{i1}^{j} ,b_{i1}^{j} ,c_{i1}^{j} ,a_{i2}^{j} ,b_{i2}^{j} ,c_{i2}^{j} , \ldots ,a_{iN}^{j} ,b_{iN}^{j} ,c_{iN}^{j} )$$
(15)

Therefore, the complete RB with an associated DB is represented by a complete chromosome C j s, shown in Fig. 8:

Fig. 8
figure 8

Encoded chromosome for tuning process

Full size image
$$C_{j} = C_{1}^{j} C_{2}^{j} C_{3}^{j} \ldots C_{M - 1}^{j} C_{M}^{j}$$
(16)

Step 2: Generating the initial population

The initial gene pool is created from the initial KB. This KB is encoded directly into a chromosome, denoted as \(C_{j}\). The remaining individuals are generated by associating an interval of performance [\(c_{h}^{\text{l}} , c_{h}^{\text{r}}\)] to every gene c h in \(C_{1} , h = 1,2, \ldots ,3NM\). Each interval of performance will be the interval of adjustment for the corresponding variable, \(c_{h} \in [c_{h}^{\text{l}} ,c_{h}^{\text{r}} ]\). If \(t \bmod 3 = 1,\) then c t is the left value of the support of a triangular fuzzy number. The triangular fuzzy number is defined by the three parameters (c t , c t+1, c t+2) and the intervals of performance are as the following:

$$\begin{aligned} c_{t} \in \left[ {c_{t}^{\text{l}} ,c_{t}^{\text{r}} } \right] = \left[ {c_{t} - \frac{{c_{t + 1} - c_{t} }}{2}, c_{t} + \frac{{c_{t + 1} - c_{t} }}{2} } \right] \hfill \\ c_{t + 1} \in \left[ {c_{t + 1}^{l} ,c_{t + 1}^{r} } \right] = \left[ {c_{t + 1} - \frac{{c_{t + 1} - c_{t} }}{2}, c_{t + 1} + \frac{{c_{t + 2} - c_{t + 1} }}{2} } \right] \hfill \\ c_{t + 2} \in \left[ {c_{t + 2}^{l} ,c_{t + 2}^{r} } \right] = \left[ {c_{t + 2} - \frac{{c_{t + 2} - c_{t + 1} }}{2}, c_{t} + \frac{{c_{t + 3} - c_{t + 2} }}{2} } \right] \hfill \\ \end{aligned}$$
(17)

Step 3: Fitness function

It is based on the mean square error (MSE) over a training data.

Step 4: Genetic operator

The GA designed for both tuning process presents a real-coding issue and uses the stochastic universal sampling as selection procedure together with an elitist scheme. The operators employed for performing the individual recombination and mutation are Michalewicz’s nonuniform mutation, and the max–min arithmetical crossover.

Particle swarm optimization for tuning fuzzy expert system (PSOFEX)

In this subsection, the database of the fuzzy expert system is tuned using PSO as follows. PSO is one of the optimization techniques and belongs to evolutionary computation techniques developed by Kennedy and Eberhart. The method has been developed through a simulation of simplified social models. The features of the method are as follows (Niknam and Amiri 2010; Asadi et al. 2012):

(1) The method is based on researches on swarms such as fish schooling and bird flocking.

(2) It is based on a simple concept. Therefore, the computation time is short and it requires few memories.

According to the research results for bird flocking, birds are finding food by flocking (not by each individual). It leads to the assumption that information is owned jointly in flocking. According to the observation of behavior of human groups, behavior pattern on each individual is based on several behavior patterns authorized by the groups, such as customs and the experiences by each individual (agent). The assumptions are basic concepts of PSO.

PSO is basically developed through simulation of bird flocking in two-dimension space. The position of each individual is represented by XY axis position and also the velocity is expressed by vx (the velocity of X axis) and vy (the velocity of Y axis). Modification of the agent position is realized by the position and velocity information.

An optimization technique based on the above concept can be described as follows: namely, bird flocking optimizes a certain objective function. Each agent knows its best value so far (pbest) and its XY position. Moreover, each agent knows the best value so far in the group (gbest) among pbests. Each agent tries to modify its position using the following information:

  • the current positions (x, y),

  • the current velocities (vx, vy),

  • the distance between the current position, and pbest and gbest.

This modification can be represented by the concept of velocity. Velocity of each agent can be modified by the following equation:

$$v_{i}^{k + 1} = w^{k} \times v_{i}^{k} + c_{1} {\text{rand}}(p{\text{best}}_{i} - s_{i}^{k} ) + c_{2} {\text{rand}} \times \left( {g{\text{best}} - s_{i}^{k} } \right)$$
(18)

where \(v_{i}^{k}\) is the velocity of agent i at iteration k, w is the weighting function, c j is the weighting factor, rand is the random number between 0 and 1, s k i is the current position of agent i at iteration k, pbest i is the best position of agent i, and gbest is the best position of group.

Using the above equation, a certain velocity, which gradually gets close to pbest and gbest, can be calculated. The current position (searching point in the solution space) can be modified by the following equation:

$$s_{i}^{k + 1} = s_{i}^{k} + v_{i}^{k + 1}$$
(19)

Figure 9 shows a searching concept with agents in a solution space and Fig. 10 shows a concept of modification of a searching point by PSO.

Fig. 9
figure 9

DEFES model prediction of IBM stock price (train & test data)

Full size image
Fig. 10
figure 10

Searching concept with agents in a solution space by PSO

Full size image

For tuning purposes, the solutions need to be encoded first. As described in “Genetic tuning process”, in PSO, particle encodings are analogous to chromosomes in the GA.

Application of the DEFES

To demonstrate the appropriateness and effectiveness of the proposed method, consider the following application in financial time series forecasting. We have used stock price data of IBM. Data are collected from http://www.finance.yahoo.com. Table 1 shows the information of the training and test datasets. As in the previous study, the four attributes: open, high, low and close price from the daily stock market are used to form the observation vector. Description of the variables is shown in Table 2. The forecast variable here is the next day’s closing price.

Table 1 Training and testing dataset
Full size table
Table 2 Variables description
Full size table

Constructing DEFES for estimating behavior of stock price

In the first stage, we use SRA to eliminate low impact factors and choose the most influential ones. The statistical software SPSS was used for applying stepwise regression analysis in this research. After the elimination process, two factors of: open and close price were selected. The selected variables will be inputted into intelligent models. In third stage, SGF is applied on collected data to make our raw data clean and smooth. It is obvious that the noisy data and outliers will cause a bad training process and, as its consequence, it will decrease the forecasting performance. By applying SGF smoothing filter, not only we do not eliminate the outliers but also we change them into suitable and useful data. We use trail-and-error process for determining the size of number of clusters, after examination of different number of clusters such as 2, 3 and 4 we obtained that in our cases the suitable number of clusters (k) that provides minimum MAPE values for test data of IBM.

In the subsequent stages with Extraction of Mamdani type fuzzy rule-based system, Rule filtering and Genetic tuning process, it builds a DEFES for each cluster using related training data. Finally, in the testing stage, the data are first clustered and stock price forecasting is done by means of each cluster’s test data. The proposed DEFES is applied for forecasting the next day’s closing price and we examined 2, 3 and 4 sub-populations and best results obtained by dividing dataset into two clusters that is shown in Table 3. The estimated value of the proposed model for both test and training data is plotted in Fig. 11. The suitable features of DEFES and number of train and test observations for each cluster and each case after examination of different feature of parameters are shown in Table 4. In Table 5, the PSO parameters used to tune the database of the fuzzy expert system (i.e., PSOFES) are shown.

Table 3 MAPE values of the forecasting results for different clusters
Full size table
Fig. 11
figure 11

Concept of modification of a searching point by PSO

Full size image
Table 4 The suitable features of DEFES for each cluster
Full size table
Table 5 The suitable features of PSOFES
Full size table

In our case, seven fuzzy rules for cluster 1 and eight fuzzy rules for cluster 2 have been evolved by DEFES to simulate the behavior of stock price shown in Fig. 12. The simulated fuzzy expert system is illustrated in Fig. 13. This fuzzy expert system formulates the mapping from the input space to output space.

Fig. 12
figure 12

The extracted rule bases of cluster 1 (left) and cluster 2 (right)

Full size image
Fig. 13
figure 13

The simulated fuzzy expert system cluster 1 (left) and cluster 2 (right)

Full size image

MAPE metric

The performance of the proposed method is measured in terms of Mean Absolute Percentage Error (MAPE). It is calculated by first taking the absolute deviation between the actual value and the forecast value. Then, the total of the ratio of deviation value with its actual value is calculated. The percentage of the average of this total ratio is the mean absolute percentage error. The following equation shows the process to calculate the MAPE (Asadi et al. 2013). The Mean Absolute Percentage Error (MAPE) is:

$${\text{MAPE}} = \frac{{\mathop \sum \nolimits_{i = 1}^{r} \left( {\frac{{{\text{abs}}\left( {p_{i} - y_{i} } \right)}}{{y_{i} }}} \right)}}{r} \times 100\;\%$$
(20)

where r is the total number of test data sequences, y i is the actual stock price on day i, and p i is the forecast stock price on day i.

Table 6 reports the forecast performance of the developed DEFES model in terms of the forecast error using the MAPE metric and compares the forecast accuracy of the developed model with other models. Table 6 testifies to superior performance of DEFES compared to other algorithms.

Table 6 Comparison of the performance of the proposed model with those of other
Full size table

Both GA and PSO are inherently probabilistic; thus, their time complexity is cannot be directly considered. Instead, we compare the algorithms’ execution times. Algorithms X and Y execute in 2435 and 1678 s, respectively. Thus, despite its higher accuracy, algorithm X requires a larger amount of time to complete.

Conclusion

Improving forecasting, especially estimating the behavior of stock price accuracy, is an important difficult task. Combining several models or using hybrid models can be an effective way to improve estimating accuracy. With neural networks, it is difficult to analyze the importance of input data and the way the network derives its results. The advantage of fuzzy expert systems is that they can explain how they derive their results. The major problem with applying fuzzy expert systems to the stock market is the difficultly in formulating knowledge of the markets because we ourselves do not completely understand them. In fact, the automatic definition of fuzzy systems can be considered as an optimization or search process. Nowadays, evolutionary algorithms, particularly genetic algorithm, are used for automatic extraction fuzzy expert systems. In this paper, it has presented a novel tool to estimate the behavior of stock price in seven stages. It is the first study on using an approximate fuzzy rule base system and evolutionary strategy with the ability of extracting whole knowledge base of fuzzy expert system for stock price forecasting problems. This tool combines data mining, fuzzy expert system, evolutionary strategy and genetic algorithm. Beginning in three stages, DEFES is equipped with data mining concept. Data mining process includes application of three preprocessing methods: noise filtering, stepwise regression and data clustering. It is used for refining and improving the tool performance. Continued genetic algorithm and evolutionary strategy extract whole knowledge base of a fuzzy expert system. To evaluate the proposed approach, we applied it to stock price data of IBM Corporation which had been used in different papers as the case study. Results have showed that forecasting accuracy of DEFES outperforms the rest of approaches regarding MAPE. So DEFES is able to cope with the fluctuations of stock price values and it can be used as a suitable tool to simulation behavior of stock price.