A stochastic model for the cell formation problem considering machine reliability

Abstract

This paper presents a new mathematical model to solve cell formation problem in cellular manufacturing systems, where inter-arrival time, processing time, and machine breakdown time are probabilistic. The objective function maximizes the number of operations of each part with more arrival rate within one cell. Because a queue behind each machine; queuing theory is used to formulate the model. To solve the model, two metaheurstic algorithms such as modified particle swarm optimization and genetic algorithm are proposed. For the generation of initial solutions in these algorithms, a new heuristic method is developed, which always creates feasible solutions. Both metaheurstic algorithms are compared against global solutions obtained from Lingo software’s branch and bound (B&B). Also, a statistical method will be used for comparison of solutions of two metaheurstic algorithms. The results of numerical examples indicate that considering the machine breakdown has significant effect on block structures of machine-part matrixes.

Introduction

The concept of group technology (GT) has emerged to reduce setups, batch sizes, and travel distances. In essence, GT tries to retain the flexibility of a job shop with the high productivity of a flow shop. Cellular manufacturing (CM) is an application of GT in a manufacturing system. CM involves processing a collection of similar parts (part families) on a dedicated cluster of machines or manufacturing processes (cells). The cell formation (CF) problem in CM systems is the decomposition of the manufacturing systems into cells (Singh and Rajamani 1996). Cellular manufacturing problems can be under static or dynamic conditions. In static conditions, CF is done for a single-period planning horizon. In real problems, some input parameters such as costs, demands, processing times, and setup times are uncertain and this uncertainty can affect the results. In the static stochastic problems, it is assumed that our information on model parameters is incomplete. In other words, the exact value of the parameters is unknown. It can only be predicted with probability; however, parameters are uncertain, static and do not change during time. In the following, a review of previous studies about static stochastic cell formation problem is presented in four parts such as processing time, the mix product, the demand, and the reliability, respectively.

Saidi-Mehrabad and Ghezavati (2009) assumed the processing time and the time between two successive arrivals to cell described by exponential distribution in the CF problem. For analyzing this problem, they used queuing theory in which machine has been considered as a server and the part as a customer. The aim of this model is to minimize the summation of three costs: (1) the idleness costs for machines (2) total cost of sub-contracting for exceptional elements, and (3) the cost of resource underutilization. Ghezavati and Saidi-Mehrabad (2010) proposed a mathematical model for the CM problem integrated with group scheduling in an uncertain space. Within this model, CF and scheduling decisions are optimized concurrently. It is assumed that processing time of parts on machines is stochastic and described by discrete scenarios. Their model minimizes the expected total cost including maximum tardiness cost among all parts, the cost of sub-contracting for exceptional elements, and the cost of resource underutilization. Egilmez and Suer (2011a, b) presented a mathematical model for CF which minimized the number of tardy jobs and total probability of tardiness. They assumed that processing time of each job has a normal distribution. Ghezavati and Saidi-Mehrabad (2011) assumed that each machine works as a server and each part is a customer where servers should provide service to customers. Accordingly, they defined formed cells as a queue system which can be optimized by queuing theory. The optimal cells and part families were formed by maximizing the probability that a server is busy. Ghezavati (2011) evaluated the CF problem, scheduling, and layout decisions, concurrently. Also, he considered processing time as stochastic with discrete scenarios under supply chain characteristics. This model minimized holding cost and the costs with respect to the suppliers network in a supply chain in order to outsource exceptional operations. Fardis et al. (2013) examined the CF problem considering that the arrival rate of parts into cells and machine service rate are stochastic parameters, which have described by an exponential distribution. The objective function of presented model minimized summation of the idleness cost of machines, the sub-contracting cost for exceptional parts, non-utilizing machine cost, and the holding cost of parts in the cells.

The mix product is defined as the set of part types in a factory which can be produced and each factory looks for the best mix product. The mix product and value of demand for each product in the mix product due to customized products, shorter product life cycles, and unpredictable patterns of demand, are not known exactly at the time of designing the manufacturing cells. The composition of the product mix is determined by demand and is probabilistic in nature. Seifoddini (1990) proposed a stochastic CF model in which for each mix product a probability had been attributed. He calculated the expected intercellular material handling cost for each machine cell arrangement under all possible product mixes. Madhusudanan Pillai and Chandrasekharan (2010) evaluated the CF problem under probabilistic product mix. Each product mix is specified with a scenario and to each scenario has been attributed probability of occurrence. They minimized inter-cell material handling. Jayakumar and Raju (2011) presented a mathematic model for the CF problem in which for each scenario probability of occurrence has been attributed. The objective function of this model is to minimize the total machine constant (investment) cost, the operating cost, the inter-cell material handling cost, and the intra-cell material handling cost for a particular product mix.

A review of studies done in the demand area is provided in the following. Cao and Chen (2005) offered CF with scenarios for product demand. In this model, an occurrence probability had been assigned for each scenario. The objective function of this model minimized machine cost and the expected inter-cell material handling cost. Tavakkoli-Moghaddam et al. (2007) examined a mathematical model to solve a facility layout problem in CM systems with stochastic demands. The main purpose of their study is to minimize the total costs of inter-cell and intra-cell movements in both machine and cell layout problems in CM system simultaneously. They considered part demands as an independent variable with the normal probability distribution. Egilmez and Suer (2011a, b) proposed a two-phase hierarchical methodology to find the optimal manpower assignment and cell loads simultaneously. In the first phase, the manufacture cells are formed with the objective function of the production rate maximization. Then, the manpower is assigned to the manufacture cells to minimize number of labors. In both the models, the processing time and demand have the normal distribution. Ariafar et al. (2011) purposed the model for cell layout in the shop and machines in the machine cells. The demand has been considered as stochastic and with a uniform distribution. This model minimizes the inter-cell and intra-cell material handling costs. Egilmez et al. (2012) considered processing times and customer demand uncertain with the normal distribution. The objective is to design a CM system with product families that are formed with the most similar products and minimum number of cells and machines for a specified risk level. Ariafar et al. (2012) examined the effect of demand fluctuation on cell layout in shop and machine layout in cell. This model minimizes the inter-cell and intra-cell material handling costs. They assumed which demand has the normal distribution. Rabbani et al. (2012) proposed a bi-objective CF problem with demand of products expressed in a number of probabilistic scenarios. Their model in the first objective minimizes the sum of machine constant cost, expected machine variable cost, cell fixed-charge cost, and expected intercell movement cost and in the second objective minimizes the expected total cell loading variation. Egilmez and Suer (2014) offered two models for analyzing the interaction between CF stage and cell scheduling stage in terms of the risk taken by decision-makers. The first model formed manufacturing cells with the objective of maximizing total pair-wise similarity among products assigned to cells and minimizing the total number of cells. The second model maximizes the number of early jobs. The demand and the processing time in both models are random variables with the normal distribution.

Jabal Ameli et al. (2008) investigated the effects of machine breakdowns in the CF problem with a new perspective. The results of their study showed that although considering machine reliability can increase the movement costs, it significantly reduces the total costs and total time for CM system. Jabal Ameli and Arkat (2008) have conducted a study on the configuration of machine cells considering production volumes and process sequences of parts. Further, they studied on alternative process routings for part types and machine reliability considerations. They found out that the reliability consideration has significant impacts on the final block diagonal form of machine-part matrixes. Chung et al. (2011) found that machine reliability has meaningful effects on reducing the total system cost in the CF problem. Arkat et al. (2011) presented the CF problem in general state and considering the reliability. The generalized CF problem follows selecting the best process plan for each part and assigning machines to the cells. In this model, it has been assumed that the number of breakdowns for each machine follows a Poisson distribution with a known failure rate. Because of the probabilistic nature of the machine breakdowns, a set of chance constraints have been introduced. These constraints guarantee that the number of breakdowns for each machine never exceeds a predefined percentile. The objective function of this model minimized intercellular and intracellular movement costs and machine breakdown costs.

Many articles investigate CM system problems in certain conditions, demand, machine availability, processing time, raw materials, and etc., but they are uncertain in real world and are changed randomly during the time horizon. Therefore, cellular manufacturing in uncertainty condition is an important area for investigation for making more accurate decisions. In this paper, uncertainty in processing time, time between two successive arrivals to cell, and reliability are considered to fill this gap in literature. The structure of this paper is as follows. In Sect. “Problem formulation”, the problem formulation is described. The MPSO algorithm and GA are described in Sect. “Notation”. The computational results and conclusion are reported in Sects. “Mathematical model” and “The proposed algorithms”, respectively.

Problem formulation

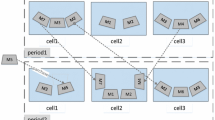
In this section, a new mathematical model is proposed for static stochastic cell formation problem. The presented model forms manufacturing cells considering three stochastic parameters including the processing time, the time between two successive arrival parts to the cell, and the machine availability, simultaneously. In this model, cells are assigned to the parts according to priority of arrival rate, i.e., at first, the cell is assigned to the part which has the most arrival rate. In fact, exceptional elements (EEs) are minimized in this way. EEs are defined as parts which must be processed in different cells, and therefore they have intercellular movements. In this paper, EEs will be outsourced to be operated. M/G/1 queuing model is used to formulate the problem and the machine is assumed as a server and the part as a customer. In the M/G/1 model, the time between two successive arrival customers is exponentially distributed and service time is generally distributed. Service discipline is based on first come, first service. In the M/G/1 model, when those entities that are lost are included, the output stream is Poisson. This assumption is supported by several empirical results which have been pointed out by these researchers in the article presented by the Cruz et al. (2010). Since the arrival rate to each queuing system is less than the service rate in the presented model, the arrival rate is equal to the output rate. Besides, the arrival time or output time of parts is exponentially distributed. The queuing system is shown in Fig. 1.

Fig. 1

An example of queuing system in the CM system

Notation

Indexing sets

• $i$ index for parts $i = 1,. . .,P$

• $j$ index for machines $j = 1,. . .,M$

• $k$ index for cells $k = 1,. . .,C$

Parameters

• $\lambda_{i}$ mean arrival rate for part $i$ (mean number of parts entered per unit time)

• $\mu_{j}$ mean service rate for machine j (mean number of customers served per unit time by machine j)

• M _max The maximum number of machines per cell

• MTBFj Mean time between failures for machine j

• MTTRj Mean time to repair for machine j

$$a_{{ij}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if part }}i\,{\text{is to be processed on machine }}j} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right.$$

Decision variables

$$ x_{{ik}} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if part }}i\,{\text{is assigned to cell }}k} \\ 0 & {{\text{otherwise}}} \\ \end{array} } \right. $$

$$ y_{jk} = \left\{ {\begin{array}{*{20}c} 1 & {{\text{if machine }}j {\text{is assigned to cell }}k} \\ 0 & {\text{otherwise}} \\ \end{array} } \right. $$

Mathematical model

Machine reliability has a probabilistic nature. It is assumed that the breakdown time for each machine follows a general distribution with known mean time to repair (MTTR) and known mean time between failures (MTBF). In this section, the reliability of machines into the CF model is discussed. The approach presented by Ameli et al. (2008) has been used for considering the reliability. For investigation of the effect of the reliability on the CF problem, two definitions are given. The number of machine breakdowns for machine j, N _j (t), can be acquired by dividing the production time for machine j, t _j, by the MTBF _j .

$$ N_{j} \left( t \right) = \frac{{t_{j} }}{{{\text{MTBF}}_{j} }}. $$

(1)

By multiplying the MTTR_j by the number of breakdowns calculated in Eq. (1), the total repair time for machine j, T _j (t), can be obtained as follows:

$$ T_{j} \left( t \right) = \frac{{t_{j} \times {\text{MTTR}}_{j} }}{{{\text{MTBF}}_{j} }}. $$

(2)

In order to obtain the total time for a machine, the repair time for the machine is added to its production time.

$$ \begin{aligned} {\text{mean of total time for machine }}j & = \frac{{E_{j} (t) \times {\text{MTTR}}_{j} }}{{{\text{MTBF}}_{j} }} + E_{j} \left( t \right) = \frac{{{\text{MTTR}}_{j} }}{{\mu_{j} \times {\text{MTBF}}_{j} }} + \frac{1}{{\mu_{j} }} \\ {\text{mean of total time for machine }}j & = \frac{1}{{\mu_{\text{j}} }}\left( {\frac{{{\text{MTTR}}_{j} + {\text{MTBF}}_{j} }}{{{\text{MTBF}}_{j} }}} \right) \\ \end{aligned}, $$

(3)

where $E_{j} \left( t \right)$ is the production time expectation for machine j. Finally, the production rate can be obtained considering the reliability as follows:

$$ {\text{the production rate for machine }}j = \mu_{j} \left( {\frac{{{\text{MTBF}}_{j} }}{{{\text{MTTR}}_{j} + {\text{MTBF}}_{j} }}} \right) $$

(4)

As might be expected, the value of production rate is reduced by considering reliability. As said by above contents, the reliability affects only on the production rate.

According to the queuing model and the Fig. 1, the inter-arrival time of parts is uncertain and it is described by the exponential distribution. Also, as each machine processes different parts with different arrival rates, according to this property, the minimum of independent exponential random variables with the arrival rate of $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{P}$ is also exponential with rate $\mathop \sum \nolimits_{i = 1}^{P} \lambda_{i}$ (Frederick and HillIer 2001). Hence, the minimum of the inter-arrival times has an exponential distribution with parameter $\lambda_{\text{eff}}$ (effective arrival rate). The $\lambda_{\text{eff}}$ can be computed as follows:

$$ \lambda_{\text{eff}} = \mathop \sum \limits_{i = 1}^{\text{P}} \lambda_{i}, $$

in which $\lambda_{i}$ is the arrival rate for the part i and $P$ is the number of parts that are processed on the same machine. Based on the presented description, the proposed model can be formulated as follows:

$$ {\text{Max }}z = \frac{1}{M}\mathop \sum \limits_{k = 1}^{\text{C}} \mathop \sum \limits_{j = 1}^{\text{M}} \mathop \sum \limits_{i = 1}^{\text{P}} \lambda_{i} {\text{a}}_{ij} {\text{x}}_{ik} {\text{y}}_{jk} $$

(5)

$$ {\text{s}}.{\text{t}}: \begin{array}{*{20}c} {\mathop \sum \limits_{k = 1}^{C} x_{ik} = 1} & {\forall i} \\ \end{array} $$

(6)

$$ \begin{array}{*{20}c} {\mathop \sum \limits_{k = 1}^{\text{C}} y_{jk} = 1} & {\forall j} \\ \end{array} $$

(7)

$$ \begin{array}{*{20}c} {\mathop \sum \limits_{j = 1}^{\text{M}} y_{jk} \le M_{ \hbox{max} } } & {\forall k} \\ \end{array} $$

(8)

$$ \begin{array}{*{20}c} {\mathop \sum \limits_{k = 1}^{\text{C}} \mathop \sum \limits_{i = 1}^{\text{P}} \lambda_{i} {\text{a}}_{ij} {\text{x}}_{ik} {\text{y}}_{jk} < \mu_{j} \left( {\frac{{{\text{MTBF}}_{j} }}{{{\text{MTTR}}_{j} + {\text{MTBF}}_{j} }}} \right)} & {\forall j} \\ \end{array} $$

(9)

$$ \begin{array}{*{20}c} {x_{ik} , y_{jk} \in \left\{ {0,1} \right\}} & {\forall i,j,k} \\ \end{array}. $$

(10)

The objective function (5) maximizes the average effective arrival rate. Maximizing the average effective arrival rate increases processing operations of the part with more arrival rate within one cell. Hence, the number of intercellular movement becomes lower. The main point in the objective function is that the arrival rate for each part is added to the effective arrival rate for each machine when part needs to be operated on the machine, and the part and the machine allowed in each cell. Constraint (6) guarantees that each part must be allocated to one cell only. Constraint (7) guarantees that each machine must be allocated to one cell only. Constraint (8) guarantees that the number of machines to be allocated to each cell should be less than the maximum number of machines allowed in each cell. Constraint (9) avoids instability of the queuing system, that is, the effective arrival rate will be necessarily less than the service rate. Constraint (10) specifies the type of decision variables.

In the proposed mathematical model, the objective function (5) and constraint (9) are nonlinear. For linearization, new binary integer variable $V_{ijk}$ is defined which is computed by the following equation:

$$ \begin{array}{*{20}c} {V_{ijk} = x_{ik} \times y_{jk} } & {\forall i,j,k} \\ \end{array}. $$

(11)

For linearization of the objective function (5) and constraint (9), the following equations should be added to the proposed model by enforcing these two linear inequalities simultaneously:

$$ \begin{array}{*{20}c} {V_{ijk} - x_{ik} - y_{jk} + 1.5 \ge 0} & {\forall i,j,k} \\ \end{array} $$

(12)

$$ \begin{array}{*{20}c} {1.5V_{ijk} - x_{ik} - y_{jk} \le 0} & {\forall i,j,k} \\ \end{array}. $$

(13)

The proposed algorithms

The CF problem is NP-hard problem (King and Nakornchai 1982). Therefore, precise solution procedures and commercial optimization softwares are unable to reach global optimum in an acceptable amount of time for medium- and large-scale problems. To deal with this deficiency, two algorithms based on MPSO and GA metheuristics have been developed in this paper.

Particle or chromosome structure

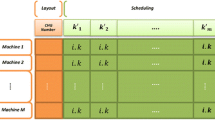
The particle representation or the chromosome representation involves two sections: the first section indicates the cells assigned to machines and the second section represents the cells assigned to parts. The used particle or the used chromosome for the proposed model has been presented in Fig. 2.

Fig. 2

The sample of particle (chromosome) structure

The proposed generating initial population

To present a qualified initial population, a heuristic method is proposed that always produces a feasible solution. The heuristic method has been presented in Fig. 3. In the first step, machines are allocated to cells based on the capacity of cells, and in the second step parts are allocated to cells considering constraint (9) for all machines.

Fig. 3

Heuristic algorithm to generate a feasible initial population

The MPSO algorithm

Particle swarm optimization (PSO) algorithm by Kennedy and Eberhart (1995), (Eberhart and Kennedy 1995) has been presented for problems which have continuous solution space. PSO is a nature-based evolutionary algorithm and starts with an initial population of random solutions. Each potential solution is called particle (${\vec{\text{x}}}$). Particles move around in a multidimensional search space, and during movement, each particle adjusts its position based on its own past and the experience of neighbor particles. Particle’s fitness is compared with its ${\text{pbest}}_{i}$ (value of the best function result so far, for particle $i$). If existing value is better than ${\text{pbest}}_{i}$, then set ${\text{pbest}}_{i}$ equal to the current value, and $p_{i}$ equal to the current location ${\vec{\text{x}}}_{\text{i}}$ in multidimensional space. Value of the best function result so far for all particles is called ${\text{gbest}}$, and its location is assigned to $p_{\text{g}}$.

In the original PSO process, the velocity of each particle is iteratively adjusted so that the particle stochastically oscillates around ${\vec{\text{p}}}_{\text{i}}$ and ${\vec{\text{p}}}_{\text{g}}$ locations. In fact, the velocity of a particle must be understood as an ordered set of transformations that operate on a solution. The MPSO algorithm uses this concept for optimizing.

The pseudocode main steps of the MPSO algorithm are as follows:

• 1. Initial population is generated using the proposed heuristic algorithm (Fig. 3).

• 2. The fitness value of all particles is calculated by the linearization objective function.

• 3. The fitness value of each particle is assigned to ${\text{pbest}}_{i}$ and its location to ${\vec{\text{p}}}_{\text{i}}$. Identification of the particle in whole swarm with the best success so far, and assignment of its fitness value to ${\text{gbest}}$ and its location to ${\vec{\text{p}}}_{\text{g}}$.

• 4. Producing a new population is based on the repetition of the following steps:

  • 4.1. A new vector P is generated to record the positions where the ${\vec{\text{x}}}_{\text{i}}$ and ${\vec{\text{p}}}_{\text{i}}$ elements are not equal. A vector Q is defined with the same length with the vector P. Binary elements for the vector Q are generated randomly.

  • 4.2. In each position of the vector Q, if the element is 0, the change is not made, but if the element is 1, the element of the same position of vector P is selected. This element in the vector P shows the position of vector ${\vec{\text{p}}}_{\text{i}}$ which should be copied in the vector ${\vec{\text{x}}}_{\text{i}}$. Then, the feasibility of constraints (8) and (9) is evaluated. The procedure continues, if it is true, otherwise, the made changes return and the next element of vector P will be tested, which is specified by the vector Q (see Fig. 4).

    Fig. 4

    

    An example for the first stage of the new population generation of the MPSO algorithm

  • 4.3. For the new location ($\overrightarrow {\text{x'}}_{\text{i}}$) a new vector P is generated to record the positions where the $\overrightarrow {\text{x'}}_{\text{i}}$ and ${\vec{\text{p}}}_{\text{g}}$ elements are not equal. A new vector Q, is defined with the same length with vector P. Binary elements for vector Q are generated randomly.

  • 4.4. In each position of vector Q, if the element is 0, the change is not made, but if the element is 1, the element of the same position of vector P is selected. This element in the vector P shows the position of vector ${\vec{\text{p}}}_{\text{g}}$ which should be copied in vector $\overrightarrow {\text{x'}}_{\text{i}}$. Then, the feasibility of constraints (8) and (9) is evaluated. The procedure continues, if it is true, otherwise, the made changes return and the next element of vector P will be tested, which is specified by vector Q.

• 5. Comparing particle’s fitness value with its ${\text{pbest}}_{i}$. If current value is better than ${\text{pbest}}_{i}$, then set ${\text{pbest}}_{\text{i}}$ equal to the current value, and set ${\vec{\text{p}}}_{\text{i}}$ equal to the current location ${\vec{\text{x}}}_{\text{i}}$. Comparing previous ${\text{gbest}}$ with current ${\text{gbest}}$. If current value is better than previous ${\text{gbest}}$, then set ${\text{gbest}}$ equal to the current value, and assign its location to ${\vec{\text{p}}}_{\text{g}}$.

• 6. Check stopping criteria (number of iterations).

• 7. If the stopping condition is not met, go to step four.

The proposed genetic algorithm

Genetic algorithms (GAs) are search algorithms based on mechanics of the natural selection and the natural genetics. GA exploits the idea of the survival of the fittest and the interbreeding population to create a novel and innovative search strategy. A population of the strings representing solution to the specified problem is maintained by GA, which then iteratively creates the new population from the old by ranking the strings and interbreeding the fittest to create the new strings, which are closer to the optimum solution to a specified problem (Venkata 2011).

The pseudocode main steps of the proposed GA are as follows:

• 1. Initial population is generated using the proposed heuristic algorithm (see Fig. 3).

• 2. The fitness value of a chromosome is calculated by the linearization of objective function.

• 3. Producing a new population is based on the repetition of the following steps:

  • 3.1. Crossover operator:

    • 3.1.1. Selection of two parent chromosomes in one population is based on the tournament selection method. Tournament selection involves running several “tournaments” among a few individuals chosen (two or three) at random from the population. The winner of each tournament (the one with the best fitness) is selected for crossover.

    • 3.1.2. Two parents are selected from the selection population. Then a number between 1 and M + P (M is the number of machines and P is the number of parts) is selected. A single crossover point on both parents’ chromosome is selected. All data beyond that point in either chromosome are swapped between the two parent chromosomes. The resulting combinations are the children. After crossover, the feasibility of constraints (8) and (9) are evaluated. The procedure continues, if it is true, otherwise, the made change returns.

  • 3.2. The fraction of the initial population is selected with a probability and then mutations are performed on them. Used mutation alters one array value in a chromosome from its initial state. A number between 1 and M + P is selected. Then, mutation operator of the source (Mahdavi et al. 2009) is used for the mutation. After mutation, the feasibility of constraints (8) and (9) are evaluated. The procedure continues, if it is true, otherwise, the made change returns.

• 4. The size of the next population is the same as the previous one, that is derived from selecting the best solutions by comparing the previous generations and the solutions generated by mutation and crossover operators.

• 5. Check stopping criteria (number of iterations).

• 6. If the stopping condition is not met, go to step two.

Computational results

For finding high-quality solutions, some computational experiments are implemented to validate and verify the proposed model and evaluate the efficiency and performance of the proposed GA and MPSO algorithms. For this purpose, 19 sample problems are defined and then solved by Lingo software’s B&B algorithm, MPSO, and GA. Finally, the generated solutions will be compared with each other using the criteria of solution quality and solving time. The proposed model is coded in the LINGO 8.0 optimization software and the proposed metaheurstic algorithms are coded in MATLAB 2010a on a computer with 2.99 GB RAM and core i3 with 3.1 GHz processor. For each problem, it is allowed to run for 5400 s (1.5 h). In the B&B algorithm (obtained by Lingo software package), if the problem can be solved in less than 5400 s (1.5 h), it is categorized as small-, medium-sized problems; otherwise, it is categorized as large-sized problems. This procedure is similar to Safaei et al. (2008). Since the efficiency of the metaheurstics algorithms depends strongly on the operators and the parameters, the design of experiments is done to set parameters. Design of experiments finds the combination of control factors that have the lowest variation, which aims for robustness in solutions. To cover different sizes, problems with small size (8 × 11), medium size (9 × 18), and large size (16 × 30) have been selected. The MPSO and GA parameters are set using a full factorial design and Taguchi technique design, respectively. A summary of all obtained MPSO and GA parameters are given in Tables 1 and 2, respectively.

Table 1 The obtained values for MPSO parameters

Table 2 The obtained values for GA parameters

According to the Lingo software’s documents, the ${\text{F}}_{\text{best}}$ shows the best feasible objective function value (OFV) which has been found so far. $F_{\text{bound}}$ indicates the bound on the objective function value. Thus, a possible domain for the optimum value of objective function ($F^{ *}$) is limited between $F_{\text{best}} \le F^{ *} \le F_{\text{bound}}$. Table 3 and Table 4 indicate the comparison of the Lingo software’s B&B algorithm results with MPSO and GA corresponding to 19 test problems for states of ignoring reliability and considering reliability, respectively. Each problem is ran 10 times and the average of OFV ($Z_{\text{ave}}$), the best OFV ($Z_{\text{best}}$), and also average of run time ($T_{\text{MPSO}}$) are represented in this two tables. The relative gap between the best OFV found by Lingo ($F_{\text{best}}$) and $Z_{\text{ave}}$ that is found by the metaheurstic algorithms are shown in column ‘‘$G_{\text{ave}}$’’. The $G_{\text{ave}}$ is calculated as $G_{\text{ave}} = \left[ {\left( {Z_{\text{ave}} - F_{\text{best}} } \right)/F_{\text{best}} } \right] \times 100$. Also, the relative gap between $F_{\text{best}}$ and $Z_{\text{best}}$ is shown in column ‘‘$G_{\text{best}}$’’. In a similar manner, the $G_{\text{best}}$ is calculated as $G_{\text{best}} = \left[ {\left( {Z_{\text{best}} - F_{\text{best}} } \right)/F_{\text{best}} } \right] \times 100$. In Lingo software’s B&B algorithm, if $F_{\text{bound}} = F_{\text{best}}$, the optimal solution is achieved. In Tables 3 and 4, in some cases, ${\text{Z}}_{\text{ave}}$ and $Z_{\text{best}}$ are between $F_{\text{bound}}$ and $F_{\text{best}}$ that shows a feasible better solution, under this condition $G_{\text{ave}}$ and $G_{\text{best}}$ are positive. But in cases where $Z_{\text{ave}}$ and $Z_{\text{best}}$ are out of the domain of $\left[ { F_{\text{best}} ,F_{\text{bound}} } \right],$ $G_{\text{ave}}$ and $G_{\text{best}}$ will be negative numbers. For comparing MPSO and GA, some columns are defined as Ga-ave, Ga-best, and R that are formulated as follows: ${\text{Ga}}^{\text{ave}} = \left( {Z_{\text{ave}}^{\text{MPSO}} - Z_{\text{ave}}^{\text{GA}} } \right)/Z_{\text{ave}}^{\text{MPSO}}$, ${\text{Ga}}^{\text{best}} = \left( {Z_{\text{best}}^{\text{MPSO}} - Z_{\text{best}}^{\text{GA}} } \right)/Z_{\text{best}}^{\text{MPSO}},$ and $R = \left( {T_{\text{MPSO}} - T_{\text{GA}} } \right)/T_{\text{GA}}$, respectively.

Table 3 Comparison of B&B, MPSO, and GA results for state of ignoring machine reliability

Table 4 Comparison of B&B, MPSO, and GA results for state of considering machine reliability

As mentioned above in small, medium-sized examples, a limited run time (1.5 h) is considered for Lingo solver to find optimal solutions. Therefore, as it can be concluded from Tables 3 and 4, the percent error of optimal solution is very low when different problems are selected. Also, in large-sized examples, MPSO and GA perform better than the Lingo software’s B&B algorithm in most problems in limited time. It implies that MPSO and GA algorithms are so effective to solve the proposed model in all class of problems. Also, performance of MPSO and GA in two states of ignoring reliability and considering reliability has been indicated in Figs. 5, 6, 7, 8, and 9. From Figs. 6, 7, 8, and 9, it can be gathered that $Z_{\text{ave}}$ and $Z_{\text{best}}$ solutions for small- and medium-sized problems are so close to $F_{\text{best}}$ and even coincided. In large-sized problems, the metaheurstic algorithms which have been used, generate better solutions from lingo software’s B&B algorithm or solve problems with negligible error. Figures 10 and 11 represent the time for solving the metaheurstic algorithms and the Lingo software’s B&B algorithm for two states of ignoring reliability and considering reliability, respectively. It is obvious that the solving time for the metaheurstic algorithms with the increasing size of the problem is much less than the Lingo software’s B&B algorithm. Two series of paired t test were conducted to analyze significant difference between the obtained solutions of the metaheurstic algorithms for two states of ignoring reliability and considering reliability, respectively. The statistical details are shown in Tables 5 and 6. Tests show that there is no statistically significant difference between solutions obtained by MPSO and GA in both states.

Fig. 5

Comparison of B&B, MPSO, and GA results (Table 3) for state of ignoring machine reliability

Fig. 6

Comparison of B&B, MPSO, and GA results (Table 3) for state of ignoring machine reliability

Fig. 7

Comparison of B&B, MPSO, and GA results (Table 4) for state of considering machine reliability

Fig. 8

Comparison of B&B, MPSO, and GA results (Table 4) for state of considering machine reliability

Fig. 9

Comparison of solving time for state of ignoring machine reliability

Fig. 10

Comparison of solving time for state of considering machine reliability

Fig. 11

Optimal solution of example 7 for state of ignoring machine reliability

Table 5 Detailed statistics of paired t test for state of ignoring machine reliability

Table 6 Detailed statistics of paired t test for state of considering machine reliability

In Table 7, the best solution obtaining from three algorithms for each problem has been used for comparison of effect of machine failure. Based on the constraint (9), the solution space of the proposed model in the state of considering machine reliability is less than the state of ignoring machine reliability. The small solution space is the reason that some values given for state of considering machine reliability are less than that for state of ignoring machine reliability. Because the objective function of this model is maximization, the values for reduction percent mentioned in Table 7 are positive. The optimal solutions of example 7 for two states of ignoring reliability and considering reliability have been given to evaluate the effect of reliability (see Figs. 11, 12). The results of solving numerical examples show that the reliability consideration has significant impacts on the final block diagonal form of machine-part matrixes. Besides, the reduction of reliability reduces the right side of the constraint (9) (see appendix A). Therefore, some operations of some parts do not process within the cell as there is an unreliable machine, although they need that machine for processing. Thus, an unreliable machine tends to form a smaller cell. The optimal solutions for example 2 for three states of MTBF of the machine 1 are presented in Figs. 13, 14, and 15. At the state MTBF = 1.9, the machine 1 cannot process any part within the cell 2 because the processing time of parts is more than the service capacity of the machine 1. Thus, those operations of parts are outsourced. Indeed, machine 1 can be deleted at this state.

Table 7 Comparison of effect of machine failure for two states of ignoring reliability and considering reliability

Fig. 12

Optimal solution of example 7 for state of considering machine reliability

Fig. 13

Optimal solution of example 2 for state of MTBF = 60

Fig. 14

Optimal solution of example 2 for state of MTBF = 4.1

Fig. 15

Optimal solution of example 2 for state of MTBF = 1.9

Conclusion and future work

In this paper, a new stochastic nonlinear model to solve CF problem within the queuing theory framework with random variables such as time between two successive arrival parts, processing time, and machine availability has been presented. To find out the optimal solution in a reasonable time, the proposed nonlinear model was linearized using auxiliary variable. The time between two successive arrival customers had exponential distribution and service time is distributed generally. Numerical examples showed that the reliability consideration has meaningful effects on the final block diagonal form of machine-part matrixes. Because of complexity class of this problem that was categorized as NP-hard, two metaheurstic algorithms based on genetic and MPSO algorithms were developed to solve problems. Also, since the efficiency of metaheurstic algorithms depends strongly on the operators and the parameters, design of experiment was done for set parameters. Deterministic method of the Lingo software’s B&B algorithm was used to evaluate the results of both metaheurstic algorithms. The results indicated that proposed metaheurstic algorithms have better performance in quality of final answer and solving time against the method of Lingo software’s B&B. For future research, considering machine capacity and costs in stochastic CF problem are offered.

Appendix A

The reliability function is expressed as

$$ R\left( t \right) = P\left( {T > t} \right) = \mathop \int \limits_{t}^{\infty } f(x){\text{dx}} $$

where $f\left( x \right)$ is the failure probability density function and $t$ is the length of the period of time (which is assumed to start from time zero). On the other hand, the MTBF can be defined in terms of the expected value of the density function $f\left( x \right)$,

$$ {\text{MTBF}} = \mathop \int \limits_{0}^{\infty } xf\left( x \right){\text{dx}}. $$

Thus,

$$ {\text{MTBF}} = \mathop \int \limits_{0}^{\infty } xf\left( x \right){\text{dx}} = \mathop \int \limits_{0}^{\infty } {\text{P}}\left( {{\text{T}} > x} \right){\text{dx}} = \mathop \int \limits_{0}^{\infty } R(x){\text{dx}}. $$

The reliability has straight relationship with the mean time between failures. Hence, reduction of the reliability reduces the right side of the constraint (9). Figure 16 is presented for more illustration of the relationship between MTBF and coefficient $\frac{\text{MTBF}}{{{\text{MTTR}} + {\text{MTBF}}}}$ of the constraint (9) in the constant value of MTTR.

Fig. 16

The relationship between MTBF and $\frac{\text{MTBF}}{\text{MTTR + MTBF}}$