A hybrid solution approach for a multi-objective closed-loop logistics network under uncertainty

Abstract

The design of closed-loop logistics (forward and reverse logistics) has attracted growing attention with the stringent pressures of customer expectations, environmental concerns and economic factors. This paper considers a multi-product, multi-period and multi-objective closed-loop logistics network model with regard to facility expansion as a facility location–allocation problem, which more closely approximates real-world conditions. A multi-objective mixed integer nonlinear programming formulation is linearized by defining new variables and adding new constraints to the model. By considering the aforementioned model under uncertainty, this paper develops a hybrid solution approach by combining an interactive fuzzy goal programming approach and robust counterpart optimization based on three well-known robust counterpart optimization formulations. Finally, this paper compares the results of the three formulations using different test scenarios and parameter-sensitive analysis in terms of the quality of the final solution, CPU time, the level of conservatism, the degree of closeness to the ideal solution, the degree of balance involved in developing a compromise solution, and satisfaction degree.

Introduction

Recently, due to increasing environmental and social concerns and associated economic benefits (Uster et al. 2007), an increasing number of companies have focused on reverse logistics in addition to forward logistics. Forward logistics encompasses material supply, production, distribution, and consumption (Krikke et al. 2003). In reverse logistics, the flow of used products includes collection, inspection/separation, recovery, disposal, and redistribution (Fleischmann et al. 2001). In a closed-loop logistics (CLL) network, which is the focus of this study, integrated management of bidirectional material movements that occur in the form of forward and reverse flows is of interest.

At the planning level, different decision-making problems arise in CLL networks. The facility location–allocation problem is one such problem, which occurs specifically at the strategic level. This type of problem includes designing a logistics configuration, selecting a facility location, assigning facilities, and determining the flow of quantity among facilities and consumers.

Real-world network design problems are often characterized by multiple and conflicting objectives. Network responsiveness is an important issue in reverse logistics. It is undesirable for customers to keep used products for an extended period of time because of the related holding costs. Therefore, companies should consider customer satisfaction in addition to minimizing costs. Optimizing such a network to trade-off between objectives is not compatible with the traditional methods. An interactive fuzzy goal programming method, by combining interactive methods, goal programming, and fuzzy programming, is highly applied to solve multi-objective problems because of its capability in controlling the satisfaction level and the compromise degree among the objectives implicitly (Torabi and Hassini 2008).

Clearly, in CLL problems, some data cannot be absolutely reliable, e.g., one can hardly believe that the demand for a product is exactly known. As an alternative, the robust optimization (RO) approach produces an uncertainty-immunized solution to an optimization problem with uncertain data. In this paper, we are interested in determining the most effective and efficient robust counterpart formulation for multi-period, multi-product and multi-objective closed-loop logistics network model that could support facility expansion with the uncertainty in the quantity of returned products and demand. Based on the aforementioned considerations, the main contributions of this research work can be described as follows:

• 1. The design and modeling of a multi-product, multi-period and multi-objective CLL network with respect to facility expansion.

• 2. The development of the proposed CLL model based on the hybridization of a robust counterpart optimization formulation and interactive fuzzy goal programming as an equivalent auxiliary crisp closed-loop logistics model (EACLLM).

• 3. A comparison of Soyster’s, Lin’s, and Bertsimas’ robust counterpart optimization formulations based on the hybrid solution approach and the proposal of an appropriate formulation for facility location-allocation problems under uncertainty.

The remainder of the paper is organized as follows: first, we present a brief review of the literature on CLL networks. Then, a generalized mixed integer non-linear programming formulation is developed to design a multi-period, multi-product and multi-objective CLL network with respect to facility expansion. The model is linearized by defining new variables and adding new constraints to the model. Then, the model is converted to an equivalent auxiliary crisp model by applying the hybridization of the robust counterpart optimization formulation (for each of the three RO formulations) and interactive fuzzy goal programming to address the uncertainty in demands and returned products with respect to multiple objectives. The computational experiments are conducted based on these three auxiliary crisp models using different test scenarios and parameter-sensitive analysis. Their performance is then evaluated in terms of the quality of the final solution, CPU time, the level of conservatism, the degree of closeness to the ideal solution, the degree of balance involved in developing a compromise solution, and satisfaction degree. Finally, conclusions are drawn and further research is discussed.

Literature review

As mentioned in the previous section, the focus of the current paper is on using a closed-loop logistics network as a combination of forward and reverse logistics. Therefore, we review papers that consider the facility location–allocation problem in CLL networks.

The minimization of total costs is the most common objective in CLL problems. In most papers, it is used as a single objective by summing different types of costs that depend on the set of decisions modeled. In contrast, multi-objective approaches have received much less attention from researchers. Most of them used fuzzy goal programming as a whole or part of their solution approach (Lee et al. 2007; Pishvaee and Torabi 2010; Mehrbod et al. 2012; Vahdani et al. 2012). Pishvaee et al. (2010) and Ramezani et al. (2013) obtained a set of pareto-optimal solutions by using a memetic algorithm and the $\varepsilon$-constraint method to deal with a multi-objective problem, respectively.

The deterministic model is the most common framework used by many researchers (Marin and Pelegrin 1998; Jayaraman et al. 1999; Fleischmann et al. 2001; Krikke et al. 2003; Lee et al. 2007a; Lu and Bostel 2007; Ko and Evans 2007; Min and Ko 2008; Lee and Dong 2008; Easwaran and Uster 2009; Wang and Hsu 2010; Zarei et al. 2010; Easwaran and Uster 2010; Mehrbod et al. 2014). Recently, because of the significance of uncertainty, more researchers have incorporated uncertain parameters into CLL networks. Listes (2007) formulated a generic stochastic model to solve a problem on a large-scale for a number of alternative scenarios. He considered a decomposition approach to this model based on the branch-and-cut procedure known as the integer L-shaped method. Lee et al. (2007b) explored a stochastic approach for a dynamic and multi-product problem. To solve the proposed model, a solution approach integrating a sample average approximation method with a simulated annealing-based heuristic algorithm was developed. In 2010, Lee et al. (2010) presented a two-stage stochastic model that accounts for a number of alternative scenarios. The model was constructed based on stochastic demand and used products with known distribution. Wang and Hsu (2010) proposed a generalized model in which stochastic demand, the reusable rate of used products, and the disposal rate are expressed by fuzzy numbers. Pishvaee et al. (2009, 2011) developed CLL networks in a stochastic programming and a robust counterpart optimization formulation, respectively. In the latter paper, a single-objective, single-product, single-period CLL problem was developed by using Ben-Tal’s robust formulation. Then, the result was compared with the deterministic model under different test scenarios. In 2010, a possibilistic mixed integer programming model was proposed to address multi-period closed-loop logistics under uncertainty by Pishvaee and Torabi (2010). To solve the proposed model, an interactive fuzzy solution approach was developed by combining a number of efficient solution approaches from the recent literature. In 2010, a CLL network was constructed under risk in a stochastic mixed integer linear programming formulation as a multi-stage stochastic program by El-Sayed et al. (2010), Vahdani et al. (2012) developed a hybrid solution approach by combining Ben-Tal’s robust optimization, queuing theory, and fuzzy programming to solve a multi-objective CLL model.

As can be seen from Table 1, a few authors considered facility expansion in their models. Ko and Evans (2007) presented a mixed integer nonlinear programming model that is a multi-period, two-echelon, multi-commodity, capacitated network design problem, considering forward and reverse flows simultaneously. In this paper, 3PLs must handle facility opening, facility closing, and expansion decisions over time to manage their networks based on the trade-offs for the various customers. Finally, to solve the model, they proposed a GA-based heuristic that consists of genetic operations and simplex transshipment algorithm.

Table 1 Review of papers in CLL network

In 2008, Min and Ko (2008) proposed a multi-product multi-period closed-loop logistics network with regard to facility expansion as a facility location-allocation problem and a genetic algorithm that can solve the mixed-integer programming model.

A more detailed classification of the literature is illustrated in Table 1. The characteristics of the problem that will be discussed in this paper are presented in the last row of Table 1. As shown in Table 1 the main difference of the problem in question compared to those discussed in the literature are the solution approach and also network structure.

Research problem

Problem definition

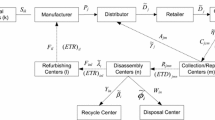
A depiction of the CLL network considered in this paper is provided in Fig. 1. The network is multi-echelon, consisting of a plant, retailers, and distribution, collection, hybrid, recovery and recycling centers. In such a logistics network, hybrid centers offer potential cost savings by hosting distribution and collection centers in the same location. In the forward flow, the plants and recovery centers are connected to retailers through distribution and hybrid centers. In the reverse flow, returned products are sent to collection and hybrid centers by retailers, and after separating, the recoverable products are shipped to recovery centers and scrapped products are carried to recycling centers. Recovered products are inserted in the forward network and are considered identical to new products.

Fig. 1

The structure of CLL network considered

Facility expansion is the process of adding capacity over time to satisfy rising demand. Facility expansion decisions in the business sector generally add up to a massive commitment of capital. The efficient investment of capital depends on making appropriate decisions in individual expansion undertakings. Planning for facility expansion consists, primarily, of determining future expansion times, sizes, and locations to support anticipated demand growth. This activity forms a crucial part of the strategic level decision making in many applications. Examples can be found in heavy process industries (Sahinidis and Grossmann 1992), communication networks (Laguna 1998), electric utilities (Murphy and Weiss 1990), automobile industries (Eppen et al. 1989), service industries (Berman and Ganz 1994), and in electronic goods and semiconductor industries (Swaminathan 2000).

This model, unlike the existing location models, considers facility expansion over time to manage the network based on the trade-offs for various situations. Thus, we may increase the utilization rate of facilities and decrease the total cost in addition to more closely approximating real cases.

We consider a decision horizon that includes multiple-periods and multiple-products in the proposed model. The flow quantities between facilities belonging to different echelons are determined according to demand, return, and other periodic-based parameters during each period. As such, this paper assumes that the demand for products and the number of returned products are uncertain over the planning time horizon.

The other main assumptions used in the problem formulation are as follows:

• a) All returned products from retailers must be collected, and all demand from retailers must be satisfied.

• b) There is no direct connection between plants/recovery/recycling centers and retailers in either direction.

• c) A recycling center is a storage place for scrapped products. Therefore, we do not consider any processing cost for this type of facility.

• d) There is no missing product during the process of forward logistics.

• e) The model supported facility expansion for each facility except for plants and recycling centers.

In this network, cost minimization and the minimization of the total delivery and collection times are considered the two major objectives. The first objective is related to supply chain network efficiency, and the second is related to network responsiveness. Optimizing the network involves trade-offs between these two objectives.

Model formulation

The following notation is used in the formulation of the CLL problem.

I, i\ J, j\ K, k\ L, l\ R, r\ S, s :

Set and index of plants\ distribution\ retailer\ collection\ recovery\ recycling centers;

P, p :

Set and index of products;

T, t :

And index of time periods;

$AC_{p}$ :

Per unit storage capacity by product p;

$AR_{kp}^{t}$ :

Rate of return percentage of product p from retailer k at period t;

$AS_{p}^{t}$ :

Rate of unrecoverable percentage of product p at period t;

CD\CC:

Cost of delay in product delivery\collection for per product in per unit of time;

$CI_{ip}$ :

Maximum production capacity of plant i for product p at each period;

$CJ_{j} /CL_{l} /CR_{r} /CS_{s}$ :

Maximum capacity of distribution center j\collection center l\recovery center r\recycling center s at each period;

$\widetilde{DP}_{kp}^{t}$ :

Demand of product p at retailer k at time period t;

$EC_{kp}^{t}$ :

Expected collection time of product p for retailer k at period t;

$ED_{kp}^{t}$ :

Expected delivery time of product p for retailer k at period t;

$EJ_{j}^{t} /EL_{l}^{t} /ER_{r}^{t}$ :

Operating cost of expanding standard size in distribution center j\collection center l\recovery center r at period t;

$FH_{h}^{t}$ :

Fixed saving cost associated with opening distribution centers and collection center at location h at period t, $h \in H,\quad H \subset J,\quad H \subset L$;

$FJ_{j}^{t} /FL_{l}^{t} /FR_{r}^{t} /FS_{s}^{t}$ :

Fixed cost of opening distribution center j\collection center l\recovery center r\recycling center s at period t;

$GJ_{j} \backslash GL_{l} \backslash GR_{r}$ :

Standard expansion size of distribution center j\collection center l\recovery center r;

$MJ_{j}^{t} /ML_{l}^{t} /MR_{r}^{t}$ :

Maximum number for standard expansion size of distribution center j\collection center l\recovery center r at period t;

$PI_{ip}$ :

Manufacturing cost per unit of product p at plant i;

$PJ_{jp} /PL_{lp}$ :

Processing cost per unit of product p at distribution center j\collection center l;

$PR_{rp}$ :

Remanufacturing cost per unit of product p at recovery center r;

$TC_{klp}$ :

Collection time of product p from retailer k by collection center l;

$TD_{jkp}$ :

Delivery time of product p from distribution center j to retailer k;

$D^{t} = \left\{ {j\left| {TD_{jkp} \ge ED_{kp} } \right.} \right\}$ :

And $C^{t} \left\{ {l\left| {TC_{klp} \ge EC_{kp} } \right.} \right\}$ at period t;

$TI_{ijp} /TJ_{jkp} /TK_{klp} /TL_{lrp} /TS_{lsp} /TR_{rjp}$ :

Transportation cost per unit of product p from i to j\ j to k\ k to l\ l to r\ l to s\ r to j;

$QI_{ijp}^{t}$ :

Quantity of product p shipped from plant i to distribution center j at period t;

$QJ_{jkp}^{t}$ :

Quantity of product p shipped from distribution center j to retailer k at period t;

$QK_{klp}^{t}$ :

Quantity of product p shipped from retailer k to collection center l at period t;

$QL_{lrp}^{t}$ :

Quantity of product p shipped from collection center l to recovery center r at period t;

$QR_{rjp}^{t}$ :

Quantity of product p shipped from recovery center r to distribution center j at period t;

$QS_{lsp}^{t}$ :

Quantity of product p shipped from collection center l to recycling center s at period t;

$XJ_{j}^{t} = 1$ :

If a distribution center is opened at location j at period t, zero otherwise;

$XL_{l}^{t} = 1$ :

If a collection center is opened at location l at period t, zero otherwise;

$XR_{r}^{t} = 1$ :

If a recovery center is opened at location r at period t, zero otherwise;

$XS_{s}^{t} = 1$ :

If a recycling center is opened at location s at period t, zero otherwise;

$ZJ_{j}^{t} /ZL_{l}^{t} /ZR_{r}^{t}$ :

Number of standardized expansion in distribution center j\collection center l\recovery center r at period t;

The CLL problem can be formulated as follows:

$$ {\text{Min }}Z_{1} = {\text{Opening cost }} + {\text{ Expansion cost }} + {\text{ Transportation cost }} + {\text{ Processing cost}} $$

(1)

$$ \begin{gathered} \sum\nolimits_{j} {FJ_{j}^{1} XJ_{j}^{1} } + \sum\nolimits_{t \ge 2} {\sum\nolimits_{j} {FJ_{j}^{t} } } XJ_{j}^{t} \left( {1 - XJ_{j}^{t - 1} } \right) + \hfill \\ \sum\nolimits_{l} {FL_{l}^{1} XL_{l}^{1} } + \sum\nolimits_{t \ge 2} {\sum\nolimits_{l} {FL_{l}^{t} } } XL_{l}^{t} \left( {1 - XL_{l}^{t - 1} } \right) + \hfill \\ \sum\nolimits_{r} {FR_{r}^{1} XR_{r}^{1} } + \sum\nolimits_{t \ge 2} {\sum\nolimits_{r} {FR_{r}^{t} } } XR_{r}^{t} \left( {1 - XR_{r}^{t - 1} } \right) + \hfill \\ \sum\nolimits_{s} {FS_{s}^{1} XS_{s}^{1} } + \sum\nolimits_{t \ge 2} {\sum\nolimits_{s} {FS_{s}^{t} } } XS_{s}^{t} \left( {1 - XS_{s}^{t - 1} } \right) - \hfill \\ \sum\nolimits_{h = j = l} {FH_{h}^{1} XJ_{h}^{1} XL_{h}^{1} } - \sum\nolimits_{t \ge 2} {\sum\nolimits_{h = j = l} {FH_{h}^{t} } } XJ_{h}^{t} XL_{h}^{t} \left( {1 - XJ_{h}^{t - 1} XL_{h}^{t - 1} } \right) \hfill \\ + \sum\nolimits_{t} {\sum\nolimits_{j} {EJ_{j}^{t} } } ZJ_{j}^{t} + \sum\nolimits_{t} {\sum\nolimits_{l} {EL_{l}^{t} } } ZL_{l}^{t} + \sum\nolimits_{t} {\sum\nolimits_{r} {ER_{r}^{t} } } ZR_{r}^{t} \hfill \\ + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{j} {\sum\nolimits_{i} {TI_{ijp} QI_{ijp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{k} {\sum\nolimits_{j} {TJ_{jkp} QJ_{jkp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{l} {\sum\nolimits_{k} {TK_{klp} QK_{klp}^{t} } } } } \hfill \\ + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{r} {\sum\nolimits_{l} {TL_{lrp} QL_{lrp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{s} {\sum\nolimits_{l} {TS_{lsp} QS_{lsp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{j} {\sum\nolimits_{r} {TR_{rjp} QR_{rjp}^{t} } } } } \hfill \\ + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{j} {\sum\nolimits_{i} {PI_{ip} QI_{ijp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{k} {\sum\nolimits_{j} {PJ_{jp} QJ_{jkp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{r} {\sum\nolimits_{l} {PL_{lp} Ql_{lrp}^{t} } } } } \hfill \\ + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{s} {\sum\nolimits_{l} {PL_{lp} QS_{lsp}^{t} } } } } + \sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{j} {\sum\nolimits_{r} {PR_{rp} QR_{rjp}^{t} } } } } + \hfill \\ \end{gathered} $$

$$ \begin{gathered} {\text{Min Z}}_{ 2} = {\text{ Delivery time }} + {\text{ Collection time}} \hfill \\ CD\sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{k} {\sum\nolimits_{{j \in D^{t} }} {(TD_{jkp} } } } } - ED_{kp}^{t} )\;QJ_{jkp}^{t} + CC\sum\nolimits_{t} {\sum\nolimits_{p} {\sum\nolimits_{k} {\sum\nolimits_{{l \in C^{t} }} {(TC_{klp} } } } } - EC_{kp}^{t} )\;QK_{klp}^{t} \hfill \\ \end{gathered} $$

(2)

subject to:

$$ \sum\nolimits_{j} {QJ_{jkp}^{t} } \ge DP_{kp}^{t} \quad \forall t,\;p,\;k $$

(3)

$$ \sum\nolimits_{l} {QK_{klp}^{t} } \ge AR_{kp}^{t} DP_{kp}^{t} \quad \forall t,\;p,\;k $$

(4)

$$ \sum\nolimits_{i} {QI_{ijp}^{t} } + \sum\nolimits_{r} {QR_{rjp}^{t} } = \sum\nolimits_{k} {QJ_{jkp}^{t} } \quad \forall t,\;p,\;j $$

(5)

$$ (1 - AS_{p}^{t} )\;\sum\nolimits_{k} {QK_{klp}^{t} } = \sum\nolimits_{r} {QL_{lrp}^{t} } \quad \forall t,\;p,\;l $$

(6)

$$ AS_{p}^{t} \sum\nolimits_{k} {QK_{klp}^{t} = \sum\nolimits_{s} {QS_{lsp}^{t} } } \quad \forall t,\;p,\;l $$

(7)

$$ \sum\nolimits_{l} {QL_{lrp}^{t} } = \sum\nolimits_{j} {QR_{rjp}^{t} } \quad \forall t,\;\;p,\;\;r $$

(8)

$$ \sum\nolimits_{j} {QI_{ijp}^{t} } \le CI_{ip} \quad \forall t,\;p,\;i $$

(9)

$$ \sum\nolimits_{p} {AC_{p} } (\sum\nolimits_{i} {QI_{ijp}^{t} } + \sum\nolimits_{r} {QR_{rjp}^{t} ) \le CJ_{j} XJ_{j}^{t} + \sum\limits_{\theta = 1}^{t} {GJ_{j}^{{}} ZJ_{j}^{\theta } } } \quad \forall t,\;j $$

(10)

$$ \sum\nolimits_{p} {AC_{p} \sum\nolimits_{k} {QK_{klp}^{t} } } \le CL_{l} XL_{l}^{t} + \sum\limits_{\theta = 1}^{t} {GL_{l}^{{}} } ZL_{l}^{\theta } \quad \forall t,\;l $$

(11)

$$ \sum\nolimits_{p} {AC_{p} \sum\nolimits_{l} {QL_{lrp}^{t} \le CR_{r} XR_{r}^{t} } } + \sum\limits_{\theta = 1}^{t} {GR_{r}^{{}} } ZR_{r}^{\theta } \quad \forall t,\;r $$

(12)

$$ \sum\nolimits_{p} {AC_{p} \sum\nolimits_{l} {QS_{lsp}^{t} } } \le CS_{s} XS_{s}^{t} \quad \forall t,\;s $$

(13)

$$ XJ_{j}^{t + 1} \ge XJ_{j}^{t} \quad \forall t,\;j $$

(14)

$$ XL_{l}^{t + 1} \ge XL_{l}^{t} \quad \forall t,\;l $$

(15)

$$ XR_{r}^{t + 1} \ge XR_{r}^{t} \quad \forall t,\;r $$

(16)

$$ XS_{s}^{t + 1} \ge XS_{s}^{t} \quad \forall t,\;s $$

(17)

$$ ZJ_{j}^{t} \le MJ_{j}^{t} *XJ_{j}^{t} \quad \forall t,\;j $$

(18)

$$ ZL_{l}^{t} \le ML_{l}^{t} *XL_{l}^{t} \quad \forall t,\;l $$

(19)

$$ ZR_{r}^{t} \le MR_{r}^{t} *XR_{r}^{t} \quad \forall t,\;r $$

(20)

$$ XJ_{j}^{t} ,\;XL_{l}^{t} ,\;XR_{r}^{t} ,\;XS_{s}^{t} \in \{ 0,1\} \quad \forall t,\;j,\;r,\;l,\;s $$

(21)

$$ QI_{ijp}^{t} ,QJ_{jkp}^{t} ,\;QK_{klp}^{t} ,\;QL_{lrp}^{t} ,\;QS_{lsp}^{t} ,\;QR_{rjp}^{t} \ge 0\quad \forall t,\;p,\;i,\;j,\;k,\;l,\;r,\;s $$

(22)

$$ ZJ_{j}^{t} ,\;ZL_{l}^{t} ,\;ZR_{r}^{t}\quad \text{integer} \quad \forall t,\;j,\;l,\;r $$

(23)

Constraint (3) ensures that the demands of all of the customers are satisfied. Constraint (4) ensures that the returned products from all of the customers are collected. Constraints (5, 6, 7, 8) impose the flow balance at the distribution, collection, recovery and recycling centers. Constraints (9, 10, 11, 12, 13) are capacity constraints on facilities, including that on expansion size over the time period, prohibiting a certain number of products, returned products, and recoverable and recyclable products from being transferred to facilities that are not open. Constraints (14, 15, 16, 17) guarantee that the open facilities cannot be closed during the following periods. Constraints (18, 19, 20) ensure that the expansion of a facility is only possible if the facility has already been opened and impose a maximum standardized expansion for each type of facility at each time period. Finally, Constraints (21, 22, 23) enforce binary, non-negativity, and integer restrictions on decision variables.

In the objective function, there are several nonlinear terms to be considered. These are associated with the fixed cost of opening distribution, collection, recovery, and recycling centers and the fixed savings cost of a hybrid facility. Each of them involves the multiplication of two binary variables $(XJ_{j}^{t} ,XJ_{j}^{t - 1} )$, $(XL_{l}^{t} ,XL_{l}^{t - 1} )$, $(XR_{r}^{t} ,XR_{r}^{t - 1} )$, $(XS_{s}^{t} ,XS_{s}^{t - 1} ),$ and $(XJ_{h}^{t} ,XL_{h}^{t} )$. Therefore, the above model is linearized by defining new variables as follows.

First, using $X^{\prime}J_{j}^{t} = XJ_{j}^{t} \left( {1 - XJ_{j}^{t - 1} } \right)$, the following constraints are added to the model:

$$ XJ_{j}^{t} + XJ_{j}^{t - 1} + X^{\prime}J_{j}^{t} \le 2\quad \quad \forall t \ge 2,\;j $$

(24)

$$ XJ_{j}^{t} + XJ_{j}^{t - 1} - X^{\prime}J_{j}^{t} \ge 0\quad \quad \forall t \ge 2,\;j $$

(25)

$$ 2XJ_{j}^{t} - XJ_{j}^{t - 1} - X^{\prime}J_{j}^{t} \le 1\quad \quad \forall t \ge 2,\;j $$

(26)

$$ - 2XJ_{j}^{t} + XJ_{j}^{t - 1} + X^{\prime}J_{j}^{t} \le 1\quad \quad \forall t \ge 2,\;j $$

(27)

Constraint (24) ensures that if $XJ_{j}^{t} = 1$ and $XJ_{j}^{t - 1} = 1$, $X^{\prime}J_{j}^{t}$ should be zero; constraint (25) ensures that if $XJ_{j}^{t} = 0$ and $XJ_{j}^{t - 1} = 0$, $X^{\prime}J_{j}^{t}$ should be zero; constraint (26) ensures that if $XJ_{j}^{t} = 1$ and $XJ_{j}^{t - 1} = 0$, $X^{\prime}J_{j}^{t}$ should be one; and constraint (27) ensures that if $XJ_{j}^{t} = 0$ and $XJ_{j}^{t - 1} = 1$, $X^{\prime}J_{j}^{t}$ should be zero.

Second, using $X^{\prime}L_{l}^{t} = XL_{l}^{t} \left( {1 - XL_{l}^{t - 1} } \right)$, $X^{\prime}R_{r}^{t} = XR_{r}^{t} \left( {1 - XR_{r}^{t - 1} } \right)$, and $X^{\prime}S_{s}^{t} = XS_{s}^{t} \left( {1 - XS_{s}^{t - 1} } \right)$, based on the same logic was applied for the fixed cost of opening a distribution center, the following constraints should also be added to the model:

$$ XL_{l}^{t} + XL_{l}^{t - 1} + X^{\prime}L_{l}^{t} \le 2\quad \quad \forall t \ge 2,\;l $$

(28)

$$ XL_{l}^{t} + XL_{l}^{t - 1} - X^{\prime}L_{l}^{t} \ge 0\quad \quad \forall t \ge 2,\;l $$

(29)

$$ 2XL_{l}^{t} - XL_{l}^{t - 1} - X^{\prime}L_{l}^{t} \le 1\quad \quad \forall t \ge 2,\;l $$

(30)

$$ - 2XL_{l}^{t} + XL_{l}^{t - 1} + X^{\prime}L_{l}^{t} \le 1\quad \quad \forall t \ge 2,\;l $$

(31)

$$ XR_{r}^{t} + XR_{r}^{t - 1} + X^{\prime}R_{r}^{t} \le 2\quad \quad \forall t \ge 2,\;r $$

(32)

$$ XR_{r}^{t} + XR_{r}^{t - 1} - X^{\prime}R_{r}^{t} \ge 0\quad \quad \forall t \ge 2,\;r $$

(33)

$$ 2XR_{r}^{t} - XR_{r}^{t - 1} - X^{\prime}R_{r}^{t} \le 1\quad \quad \forall t \ge 2,\;r $$

(34)

$$ - 2XR_{r}^{t} + XR_{r}^{t - 1} + X^{\prime}R_{r}^{t} \le 1\quad \quad \forall t \ge 2,\;r $$

(35)

$$ XS_{s}^{t} + XS_{s}^{t - 1} + X^{\prime}S_{s}^{t} \le 2\quad \quad \forall t \ge 2,\;s $$

(36)

$$ XS_{s}^{t} + XS_{s}^{t - 1} - X^{\prime}S_{s}^{t} \ge 0\quad \quad \forall t \ge 2,\;s $$

(37)

$$ 2XS_{s}^{t} - XS_{s}^{t - 1} - X^{\prime}S_{s}^{t} \le 1\quad \quad \forall t \ge 2,\;s $$

(38)

$$ - 2XS_{s}^{t} + XS_{s}^{t - 1} + X^{\prime}S_{s}^{t} \le 1\quad \quad \forall t \ge 2,\;s $$

(39)

Finally, the nonlinear terms, with respect to the fixed savings cost of a hybrid facility, are linearized through following two steps.

In the first step, a new variable $XH_{h = j = l}^{t} = XJ_{j}^{t} XL_{l}^{t}$ is defined as.

$XH_{h = j = l}^{t} = 1$ if a distribution center and a collection center are opened at location $h$ in period t and zero otherwise. According to the new variable, the transformed terms are

$$ \sum\nolimits_{t = 1} {\sum\nolimits_{h = j = l} {FH_{h}^{1} } } XH_{h}^{1} - \sum\nolimits_{t \ge 2} {\sum\nolimits_{h = j = l} {FH_{h}^{t} } } XH_{h}^{t} \left( {1 - XH_{h}^{t - 1} } \right) $$

However, though the objective function minimizes costs, it has a tendency to make the value of the variable $XH_{h}^{t}$ equal to 1, and we should only limit the value of $XH_{h}^{t}$ to 1 when both $XJ_{j}^{t}$ and $XL_{l}^{t}$ are equal to 1. This can be achieved by adding the following constraints to the model.

$$ 2XH_{h = j = l}^{t} \le XJ_{j}^{t} + XL_{l}^{t} \quad \forall t,\;j,\;l $$

(40)

$$ - XH_{h = j = l}^{t} + XJ_{j}^{t} + XL_{l}^{t} \le 1\quad \forall t,j,l $$

(41)

In the second step, using $X^{\prime}H_{h}^{t} = XH_{h}^{t} \left( {1 - XH_{h}^{t - 1} } \right)$, based on the same logic that was applied for the fixed cost of opening other centers, the following constraints should be added to the model:

$$ XH_{h}^{t} + XH_{h}^{t - 1} + X^{\prime}H_{h}^{t} \le 2\quad \quad \forall t \ge 2,\;h $$

(42)

$$ XH_{h}^{t} + XH_{h}^{t - 1} - X^{\prime}H_{h}^{t} \ge 0\quad \quad \forall t \ge 2,\;h $$

(43)

$$ 2XH_{h}^{t} - XH_{h}^{t - 1} - X^{\prime}H_{h}^{t} \le 1\quad \quad \forall t \ge 2,\;h $$

(44)

$$ - 2XH_{h}^{t} + XH_{h}^{t - 1} + X^{\prime}H_{h}^{t} \le 1\quad \quad \forall t \ge 2,\;h $$

(45)

Solution approach

The proposed CLL network model is a multi-objective mixed integer linear programming formulation under uncertainty. To solve this model, a two-phase approach is proposed. In the first phase, the original model is formulated into a robust counterpart optimization problem by applying three well-known robust optimization formulations. Then, in the second phase, using an interactive fuzzy goal programming method, each of the robust optimization models is converted to an equivalent auxiliary crisp closed-loop logistics model (EACLLM) to find the final preferred compromise solution.

Robust optimization formulations

Sensitivity analysis (SA) and stochastic optimization (SO) are two classical approaches to addressing parameter uncertainty. The goal of SA is only to analyze a solution, not to produce a solution that is uncertainty-immunized to data changes (Mulvey and Vanderbei 1995).

Under SO, the feasibility of a solution is determined by chance constraints; these constraints can destroy the convexity properties and considerably increase the level of complexity of the initial model (Sim 2004). They immunize the solution in some probabilistic sense to stochastic uncertainty.

A more recent approach to optimization under uncertainty is robust optimization (RO). In contrast to SO, RO does not require uncertainty data with a known probability distribution and chance constraints. Unlike SO, RO generates a solution that is optimal for all realization of uncertain data. In the following section, we present the three most well-known RO formulations based on the nominal mixed integer linear model below:

$$ \begin{gathered} {\text{Minimize cx}} \hfill \\ {\text{s}}.{\text{t}}\;\sum\limits_{j} {a_{ij} x_{j} \le b_{i} } \quad \quad \forall i \hfill \\ \;\;\;\;L \le x \le U \hfill \\ x_{j} \;{\text{binary or continuous}}\;\forall j \hfill \\ \end{gathered} $$

(46)

In this paper, we assume that data uncertainty affects only the elements of the right-hand-side (RHS) column coefficients. To address the assumption in Soyster’s and Bertsimas’ RO formulations, we can introduce a new variable $x_{n + 1}$, which is a binary variable with a fixed value of 1, and rewrite model (46) as follows:

$$ \begin{gathered} {\text{Minimize cx}} \hfill \\ {\text{s}}.{\text{t}}\;\sum\limits_{j} {a_{ij} x_{j} - \widetilde{b}_{i} } x_{n + 1} \le 0\quad \quad \forall i \hfill \\ \;\;\;\;L \le x \le U \hfill \\ x_{j} \;{\text{binary or continuous}}\;\forall j \hfill \\ 1 \le x_{n + 1} \le 1 \hfill \\ \end{gathered} $$

(47)

The uncertainty parameter, $\widetilde{b}_{i}$, takes on values according to a symmetric distribution with a mean equal to the nominal value $b_{i}$ in the interval $[b_{i} - \widehat{b}_{i} ,b_{i} + \widehat{b}_{i} ]$, where $\widehat{b}_{i}$ represents the variation amplitude.

Soyster’s formulation

Soyster (1973) was one of the first researchers to propose a RO formulation to produce a solution that is feasible for any realization of uncertain data that belong to a convex set. The formulation admits the maximum degree of conservatism.

$$ \begin{gathered} {\text{Minimize}}\quad cx \hfill \\ {\rm s.t}\quad \quad \sum\limits_{j} {a_{ij} } x_{j} + \sum\limits_{{j \in J_{i} }} {\hat{a}_{ij} } u_{j} \le b_{i} \quad \forall i \hfill \\ \quad \quad \quad \quad \quad L \le x \le U \hfill \\ \quad \quad \quad \quad \quad - u_{j} \le x_{j} \le u_{j} \quad \forall j \hfill \\ \quad \quad \quad \quad \quad u_{j} \ge 0\quad \quad \quad \;\;\;\,{\kern 1pt} {\kern 1pt} \forall j \hfill \\ \end{gathered} $$

(48)

where $J_{i}$ is the set of coefficients in row i that are subject to uncertainty. Each entry $a_{ij} ,\;j \in J_{i}$ is formulated as a symmetric and bounded random variable $\tilde{a}_{ij} ,\;j \in J_{i}$ (Ben-Tal and Nemirovski 2000) that takes on values $\left[ {a_{ij} - \hat{a}_{ij} ,\;\,a_{ij} + \hat{a}_{ij} } \right].$ Based on the above formulation, model (47) adopts the following form:

$$ \begin{gathered} {\text{Minimize cx}} \hfill \\ {\rm s.t}\quad \quad \sum\limits_{j} {a_{ij} x_{j} - b_{i} } x_{n + 1} - \hat{b}_{i} u_{n + 1} \le 0\quad \forall i \hfill \\ \quad \quad \quad \quad L \le x \le U \hfill \\ \quad \quad \quad \quad {\text{x}}_{j} {\text{ binary or continuous}}\quad \forall {\text{j}} \hfill \\ \quad \quad \quad \quad 1 \le x_{n + 1} \le 1,\; - u_{n + 1} \le x_{n + 1} \le u_{n + 1} \hfill \\ \end{gathered} $$

(49)

As seen, in this formulation, the maximum variation is considered that affords the highest protection against uncertainty.

Lin’s formulation

To address the extreme conservatism in Soyster’s formulation, Ben-Tal and Nemirovski (2000) developed a number of RO formulations and applications and presented a detailed analysis of the RO framework in linear programming. In 2004, Lin et al. (2004) extended Ben-Tal’s formulation to mixed integer programming problems as follows:

$$ \begin{gathered} {\text{Minimize}}\quad cx \hfill \\ {\rm s.t}\quad \sum\limits_{j} {a_{ij} x_{j} } + \varepsilon \left[ {\sum\limits_{{j \in J_{i} }} {\left| {a_{ij} } \right|u_{ij} + \varOmega \sqrt {\sum\limits_{{j \in J_{i} }} {a_{ij}^{2} z_{ij}^{2} + b_{i}^{2} } } } } \right] \hfill \\ \quad \quad \quad \quad \quad \le b_{i} + \delta \hbox{max} \;\left[ {1,\left| {b_{i} } \right|} \right]\quad \forall i \hfill \\ \quad \quad \quad \quad \quad - u_{ij} \le x_{j} - z_{ij} \le u_{ij} \quad \forall i,j \hfill \\ \quad \quad \quad \quad \quad L \le x \le U \hfill \\ \end{gathered} $$

(50)

where the coefficient and the right-hand-side parameters (respectively $a_{ij} \;{\text{and}}\;b_{i}$) in row i are subject to uncertainty.

In the following, we present model (46) according to the Lin’s formulation for bounded and symmetric uncertainty:

$$ \begin{gathered} {\text{Minimize}}\quad cx \hfill \\ {\rm s.t}\quad \quad \sum\limits_{j} {a_{ij} x_{j} } + \varepsilon \varOmega b_{i} \le b_{i} + \delta \hbox{max} \left[ {1,\left| {b_{i} } \right|} \right]\quad \forall i \hfill \\ \quad \quad \quad L \le x \le U \hfill \\ \quad \quad \quad x_{j} \,{\text{binary}}\;{\text{or}}\;{\text{continuous}}\quad \forall j \hfill \\ \end{gathered} $$

(51)

where δ and ε are infeasibility tolerance and uncertainty level, respectively. Assume that the uncertain data are distributed as follows:

$$ \widetilde{b}_{i} = \left( {1 + \varepsilon \xi_{i} } \right)\;b_{i} $$

(52)

where ξi are random variables that are distributed symmetrically over the interval [−1,1]. As shown by the authors (Lin et al. 2004), in this formulation, the probability that the i constraint is violated is at most k = exp(${{ - \varOmega_{i}^{2} } \mathord{\left/ {\vphantom {{ - \varOmega_{i}^{2} } 2}} \right. \kern-0pt} 2}$), where $\varOmega$ is a positive parameter that depends on the decision maker to tradeoff robustness and quality of the solution.

Bertsimas’ formulation

Because Ben-Tal’s formulation leads to a non-linear model and no guarantee regarding the probability that the robust solution is feasible, it is highly desirable to develop a method that addresses these drawbacks. Bertsimas and Sim (2004) proposed a new RO formulation with a parameter $\varGamma_{i}$ for every constraint. In this formulation, each uncertainty parameter is assumed to take on a value from within a symmetric interval around a nominal value, and the parameter $\varGamma_{i}$ for each constraint limits the uncertainty parameters that can simultaneously take on their worst-case value. The parameter $\varGamma_{i}$ controls the trade-off between the probability of violation and the effect to the objective function of the nominal problem. They proposed the following non-linear formulation:

$$ \begin{gathered} {\text{Minimize}}\quad cx \hfill \\ {\rm s.t}\quad \quad \sum\limits_{j} {a_{ij} x_{j} } + \hfill \\ \quad \quad \quad \mathop {\hbox{max} }\limits_{{\left\{ {S_{i} \cup \left. {\left\{ {t_{i} } \right\}} \right|S_{i} \subseteq J_{i} ,\left| {S_{i} } \right| = \left\lfloor {\varGamma_{i} } \right\rfloor ,t_{i} \in J_{i} \backslash S_{i} } \right\}}} \left\{ {\sum\limits_{{j \in S_{i} }} {\widehat{a}_{ij} } u_{j} + (\varGamma_{i} - \left\lfloor {\varGamma_{i} } \right\rfloor )a_{{it_{i} }} u_{{t_{i} }} } \right\} \le b_{i} \quad \forall i \hfill \\ \quad \quad \quad L \le x \le U \hfill \\ \quad \quad \quad - u_{j} \le x_{j} \le u_{j} \quad \forall j \hfill \\ \quad \quad \quad u_{j} \ge 0\quad \quad \quad \;\;\;\,{\kern 1pt} {\kern 1pt} \forall j \hfill \\ \end{gathered} $$

(53)

where $J_{i} = \left\{ {j\left| {\widehat{a}_{ij} \succ 0} \right.} \right\}$, $\varGamma_{i} = \left[ {0,\left| {J_{i} } \right|} \right]$ and can also take non-integer value, $S_{i}$ represents the subset that contains $\left\lfloor {\varGamma_{i} } \right\rfloor$ uncertain parameters in the constraint, and $t_{i}$ is an index used to describe an additional uncertain parameter if $\varGamma_{i}$ is not an integer. Thus, when $\varGamma_{i} = 0$, constraint (53) is equivalent to that of the nominal problem. Similarly, if $\varGamma_{i} = \left| {J_{i} } \right|$, we have Soyster’s formulation. Therefore, this allows for an adjustment between the robustness of the formulation and the level of conservatism of the solution. The above robust formulation has an equivalent linear formulation on whose basis model (47) is rewritten as follows:

$$ \begin{gathered} {\text{Minimize}}\quad cx \hfill \\ {\rm s.t}\quad \quad \sum\limits_{j} {a_{ij} } x_{j} - b_{i} x_{n + 1} - z_{i} \varGamma_{i} - \sum\limits_{{j \in J_{i} }} {p_{ij} } \le 0\quad \forall i \hfill \\ \quad \quad \quad z_{i} + p_{ij} \ge \widehat{b}_{i} u_{n + 1} \quad \forall i,j \hfill \\ \quad \quad \quad - u_{n + 1} \le x_{n + 1} \le u_{n + 1} \hfill \\ \quad \quad \quad p_{ij} \ge 0\quad \forall i,j \hfill \\ \quad \quad \quad z_{i} \ge 0\quad \forall i \hfill \\ \quad \quad \quad u_{n + 1} \ge 0 \hfill \\ \quad \quad \quad 1 \le x_{n + 1} \le 1 \hfill \\ \quad \quad \quad L \le x \le U \hfill \\ \quad \quad \quad x_{j} \;{\text{binary}}\,{\text{or}}\,{\text{continuous}}\quad \forall j \hfill \\ \end{gathered} $$

(54)

For this robust counterpart formulation, Bertsimas and Sim calculated the probability of violation of the ith constraint. Specifically, if the uncertain coefficient parameter $\tilde{b}_{i}$ follows a symmetric distribution and takes values in the range $[b_{i} - \widehat{b}_{i} ,b_{i} + \widehat{b}_{i} ]$, then the probability that the ith constraint is violated satisfies the following constraint as follows:

$$ \begin{gathered} P\left( {\sum\limits_{j} {a_{ij} } x_{{^{j} }}^{{}} - \tilde{b}_{i} x_{n + 1}^{*} \ge 0} \right) \le \frac{1}{{2^{n} }}\left\{ {\left( {1\;\;\, - \mu } \right)\left( {_{\left\lfloor \nu \right\rfloor }^{n} } \right) + \sum\limits_{l = \left\lfloor \nu \right\rfloor + 1}^{n} {\left( {_{l}^{n} } \right)} } \right\} \hfill \\ \le \left( {1 - \mu } \right)C\left( {n,\left\lfloor \nu \right\rfloor } \right) + \sum\limits_{l = \left\lfloor \nu \right\rfloor + 1}^{n} {C\left( {n,l} \right)} \hfill \\ \end{gathered} $$

(55)

where $n = \left| {J_{i} } \right|,\;\nu = \frac{{\varGamma_{i} + n}}{2},\;{\text{and}}\;\mu = \nu - \left\lfloor \nu \right\rfloor$

$$ C(n,\;l) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{2^{n} }}\quad \quad ({\text{if}}\,l = 0\,\;{\text{or}}\;l = n)} \\ {\frac{1}{{\sqrt {2\pi } }}\sqrt {\frac{n}{(n - l)l}} .\exp \left\{ {n\;\log \left( {\frac{n}{{2\left( {n - l} \right)}}} \right) + l\;\log \left( {\frac{n - l}{l}} \right)} \right\}\quad {\text{otherwise}}} \\ \end{array} } \right. $$

Interactive fuzzy goal programming (IFGP)

In 1955, Charnes introduced goal programming (GP) in a single-objective linear programming problem (Deb 2008). The application quickly spread to a number of areas, such as multi-objective decision-making problems (Chao-Fang 2007). GP is the most popular approach used to handle multiple and conflicting objective problems. Instead of trying to optimize the objective function, the decision maker is asked to specify a goal or target value as a linguistic variable that is the most desirable value for that function. This facility makes impreciseness in a system which fuzzy set theory gives an opportunity to handle linguistic terms. The notion of a fuzzy set spread widely to various fields after Zimmermann and Zysno (1983) generalized the classical concept of connectives in fuzziness by combining an “and-operator” and an “or-operator” using a parameter γ $\in$ [0, 1] to solve fuzzy linear programming problems. Because of the nonlinear structure of these connectives in mathematical programming problems and because the efficiency of the solution yielded by the max–min operator is not guaranteed (Li et al. 2006), various approaches have been proposed to remove these deficiencies. In 2008, Torabi and Hassini (2008) developed an interactive fuzzy goal programming (IFGP) formulation based on the Lai and Hwang’s approach (Lai and Hwang 1993) and Werners’ approach (Werners 1988). They proved that not only can the new model (4) produce both unbalanced and balanced efficient solutions but also offer enough flexibility to provide different solutions based on the decision maker’s preferences.

$$ {\text{Minimize}}\quad \gamma \lambda + \left( {1 - \gamma } \right)\sum\limits_{k} {\theta_{K} \mu_{k} } \left( {Z^{k} \left( x \right)} \right) $$

(56)

$$ {\rm s.t}\quad \quad \lambda \le \mu_{k} \left( {Z^{k} \left( {\text{x}} \right)} \right)\quad \forall k = 1,2, \ldots ,K;\;x \in X $$

(57)

$$ g_{i} (x_{j} ) \le b_{i} \quad \forall i = 1,2, \ldots ,m;\;j = 1,2, \ldots .n $$

(58)

$$ x_{j} \ge 0\quad \forall j $$

(59)

$$ \lambda ,\,\lambda_{k} ,\,\gamma \in \left[ {0,1} \right] $$

(60)

where K is the total number of fuzzy objectives, $Z^{k} (x)$ denotes the kth objective function, $\mu_{k} \left( {Z^{k} \left( {\text{x}} \right)} \right)$ is the membership function of fuzzy goal k, which denotes the satisfaction degree of the kth objective function, based on the following formulation:

$$ \mu_{k} \left( {Z^{k} \left( {\text{x}} \right)} \right) = \left\{ \begin{gathered} 1 \hfill \\ \frac{{U_{k} - Z^{k} (x)}}{{U_{k} - L_{k} }} \hfill \\ 0 \hfill \\ \end{gathered} \right.\;\;\;\;\begin{array}{*{20}l} {if\quad Z^{k} \left( x \right) \le L_{k} } \\ {if\quad L_{k} < Z^{k} \left( x \right) < U_{k} } \\ {if\quad Z^{k} \left( x \right) \ge U_{k} } \\ \end{array} $$

(61)

$\theta_{k}$ represents the relative importance of objective k that is determined by the decision makers based on their preferences such that $\sum\nolimits_{k} {\theta_{k} } = 1,\;\theta_{k} \ge 0$, and γ is the coefficient of compensation defined within the interval [0, 1] that can be determined through a consensus decision-making process. The coefficient of compensation controls the minimum satisfaction degree and the compromise degree among the objectives implicitly (Torabi and Hassini 2008); in other words, it is the degree of decision makers’ willingness of to sacrifice their aspiration levels for their goals (Selim and Ozkarahan 2008). In this process, complete unanimity is not the goal and rarely possible. Constraints 58 and 59 include all constraints from the robust counterpart formulation.

According to the above discussion, in this paper, the proposed hybrid solution approach can be summarized in the following steps:

Step1: Develop the conventional linear programming formulation of the problem similar to the model presented in Sect. 3.

Step 2: Rewrite the model based on a robust optimization formulation.

Step 3: Define the uncertainty and reliability levels, if applicable.

Step 4: Solve the first objective function as a single objective problem. Continue this process K times for the K objective functions. If the decision makers select one of them as a preferred compromise solution, then go to the final step. Otherwise go to the next step.

Step 5: Evaluate the objective function at the Kth solution and determine the best lower bound (L _k ) and the worst upper bound (U _k ).

Step 6: Define the coefficient of compensation ($\gamma$) and relative importance of each objective ($\theta_{k}$).

Step 7: Determine a membership function for each objective function according to formulation 61.

Step 8: Convert the robust counterpart optimization formulation (in step 2) to EACLLM based on the IFGP model (56, 57, 58, 59, 60).

Step 9: Solve the model and present the solution to the decision makers. If the decision makers are satisfied with the solution, go to the final step. Otherwise go to the next step.

Step 10: Modify the coefficient of compensation (γ), relative importance ($\theta_{k}$), or the membership functions by considering only the following variations: a) an increase in the lower bound for the maximization objective and b) a decrease in the upper bound for the minimization objective; then, go to Step 7. Otherwise, go to the next step.

Step 11: Back to Step 3.

Step 12: Stop.

Computational experiments

To assess the performance of the three robust counterpart optimization formulations in the CLL model, all three EACLLMs are solved in CPLEX 12.2 using a PC with a 2.3-GHZ CPU and 1 GB of RAM. They are examined in two steps. In the first step, the EACLLMs are tested on 8 test scenarios with different sizes, uncertainty, and reliability levels by fixing the coefficient of compensation and relative importance. In the second step, the EACLLMs are examined based on the various coefficients of compensation and relative importance for one scenario. We set a bounded and symmetric uncertainty in demand and return products. Let us consider a demand with 40 % variability; it takes on values in the range [80,190] and has a nominal value of 135. The other parameters are generated randomly using the uniform distribution specified in Table 2.

Table 2 The value of the parameters used in the test scenarios

Different scenarios

Through EACLLM, Bertsimas’ formulation is solved based on four uncertainty levels (0, 0.2, 0.5, 1) and four reliability levels (50 %, 62.5 %, 70 %, 75 %), which indicate the probability that the constraint is violated. Under Lin’s formulation, we assume three uncertainty levels (0, 0.2, 0.5), three reliability levels with a minimum of 62.5 % (because a smaller amount causes the model to be infeasible), and an infeasibility tolerance level equal to zero. By supposing that the first objective function is the most important objective, we consider that $\gamma = 0.4$ and $\theta = 0.6$.

Table 3 shows that the results of the deterministic formulation are the same as those of Bertsimas’ and Lin’s formulations presented in Tables 4 and 5 when the uncertainty and reliability levels are zero and 75 %, respectively. In Table 3, Soyster’s formulation shows the same results obtained using Bertsimas’ formulation (Table 4) when the uncertainty level is 1 and the reliability level is 50 %. This means that for scenario 1, the cost is guaranteed to be below 33,903 with a probability of 50 % in the presence of 100 % uncertainty in the amount of demand and return products.

Table 3 Results of deterministic and Soyster’s formulations

Table 4 Results of Bertsimas’ formulation

Table 5 Results of Lin’s formulation

Comparing Bertsimas’ and Lin’s formulations in terms of the objective reveals that Bertsimas’ formulation outperforms Lin’s for all scenarios and different uncertainty and reliability levels, as shown in Tables 4 and 5. These tables show the gap between the two formulations, which widens as the scenario size and uncertainty level increase along with a decrease in reliability level. Furthermore, in Bertsimas’ formulation, the increase in CPU time with the scenario size is smaller than that in Lin’s formulation.

As summarized in Table 6, we can conclude that among the three robust formulations, Soyster’s formulation, with the highest level of conservatism, is not flexible to adjust the degree of robustness. In Lin’s formulation, this adjustment is made by changing the uncertainty level or probability of constraint violation (reliability level) or both. The combination of uncertainty and reliability levels makes Lin’s model more conservative and more likely to obtain infeasible solutions. Bertsimas’ formulation is able to adjust the degree of conservatism through the uncertainty level (level of robustness).

Table 6 Short summary of the differences between Bertsimas’ and Lin’s formulations

Different compromise solutions

In this step, EACLLMs are evaluated based on the different coefficients of compensation $\left( {\gamma = 0 - 1} \right)$ and relative importance $\left( {\theta = 0 - 1} \right)$ for one scenario (Table 7). Due to space limitations, the details of the compromise solutions obtained using the different parameters are not presented here, but can be made available upon request.

Table 7 The size of the test scenario and value of some parameters

The solutions show that in approximately 85 % of cases, Bertsimas’ EACLLM presents a better satisfaction degree for the first objective. However, this amount decreases to approximately 60 % for the second objective. For a better assessment, we analyze and compare the performance of the EACLLMs using the following distance and dispersion measures.

To determine the degree of closeness of each EACLLM to the ideal solution, we define the following family of distance functions (Torabi and Hassini 2008; Steuer 1986):

$$ \begin{gathered} {\text{D}}_{\text{p}} \left( {{\text{Z}}^{\text{k}} \left( {\text{x}} \right)} \right){ = }\left[ {\sum\limits_{\text{k = 1}}^{\text{K}} {\theta_{\text{k}}^{\text{p}} } \left( { 1 { - }\mu_{\text{k}} \left( {{\text{Z}}^{\text{k}} \left( {\text{x}} \right)} \right)} \right)^{{{\raise0.7ex\hbox{$ 1$} \!\mathord{\left/ {\vphantom { 1p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} } \right]\quad \quad \quad p \ge 1\;{\text{and integer}} \hfill \\ \hfill \\ \end{gathered} $$

(62)

where the power p is a distance parameter, p = 1, 2 indicate the longest and shortest distances, in the geometrical sense, respectively, and p = ∞ is the shortest distance, in the numerical sense. Thus, the best approach producing a preferred compromise solution is that in which the minimum $D_{p} \left( {Z^{k} \left( {\text{x}} \right)} \right)$ is achieved by the solution with respect to some p.

The range of satisfaction degrees (ARSD) is a dispersion index that is computed as follows [21]:

$$ {\text{RSD}}\left( {{\text{Z}}^{\text{k}} \left( {\text{x}} \right)} \right){ = }\mathop { \hbox{max} }\limits_{\text{k}} \left( {\mu_{\text{k}} \left( {{\text{Z}}^{\text{k}} \left( {\text{x}} \right)} \right)} \right){ - }\mathop { \hbox{min} }\limits_{\text{k}} \left( {\mu_{\text{k}} \left( {{\text{Z}}^{\text{k}} \left( {\text{x}} \right)} \right)} \right) $$

(63)

This index helps us measure the degree of balance involved in developing a compromise solution by considering the maximum difference between the satisfaction degrees of objectives.

By comparing the EACLLMs of Soyster, Bertsimas and Lin based on the above two measures over the change in γ and θ values, we can derive the following information:

• Table 8 shows the minimum distance measure over the change in γ and θ. It is clear that Bertsimas’ EACLLM presents minimum distance values for all distance parameters (p) when θ ≥ 0.3. Otherwise, Soyster’s EACLLM provides a better degree of closeness to the ideal solution than the other EACLLMs.

  Table 8 Performance comparison based on the minimum distance measure

• Table 9 shows that all three EACLLMs present almost the same dispersion measure over the change in γ and θ values for both objectives.

  Table 9 Performance comparison based on the minimum dispersion measure

• Considering the same dispersion measure for all EACLLMs, Bertsimas’ EACLLM is the best choice, with a minimum degree of closeness to the ideal solution and nearly the highest satisfaction degree with respect to both objectives for decision makers, except when θ ≤ 0.2.

• Overall, according to the above analysis (in Sects. 5.1–5.2), Bertsimas’ EACLLM presents the most effective and efficient robust counterpart formulation at least for location-allocation problems.

Facility location problems locate a set of facilities (resources) to minimize the cost of satisfying some set of demands (of the customers) with respect to some set of constraints. Facility location decisions are critical elements in strategic planning for a wide range of private and public firms. The branches of locating facilities are broad and long-lasting, influencing numerous operational and logistical decisions. High costs associated with property acquisition and facility construction make facility location or relocation projects long-term investments. Decision makers must select sites that will not only perform well according to the current system state, but also continue to be profitable for the facility’s lifetime, even as environmental factors change, populations shift, and market trends evolve. Finding robust facility locations is thus a difficult task, demanding decision makers to account for uncertain future events.

The results of paper show that the formulation proposed by Bertsimas and Sim is the most effective and efficient robust counterpart formulation for finding robust facility locations, with its unique advantages, that is,

• It does not increase the problem size substantially. From the results, we can see that the size of robust formulations do not increase much, because the increase in the number of constraints and variables is at the same scale as the number of the uncertain parameters.

• It maintains its linearity.

• It guarantees the feasibility for the robust optimization problem.

• It needs less CPU time and random-access memory (RAM) to be solved.

• It has the ability to control the degree of conservatism for every constraint.

• It provides a better final solution.

Conclusions

Unlike previous studies, which consider only a single product or single period in multi-objective function problems, this paper proposed a mathematical model for multi-period multi-product CLL problems. We considered the issue of balancing cost and delivery/collection times by considering a multi-objective model. Moreover, the model supported facility expansion for each facility except for plants and recycling centers and also considered cost savings associated with hybrid centers.

By considering multiple objectives and unknown parameters, the above CLL network was studied by developing a hybrid solution approach based on the IFGP model and three robust counterpart optimization formulations proposed by Soyster, Bertsimas, and Lin. The numerical results showed that Soyster’s EACLLM is the most conservative formulation without the ability to adjust the degree of robustness, which means it gives up too much optimality for the nominal problem. Between the other two with the ability to adjust the level of conservatism, Bertsimas proposed a more appropriate formulation based on modeling and numerical aspects. Bertsimas’ EACLLM does not increase the problem size considerably and preserves linearity. The numerical results showed that it outperforms Lin’s and Soyster’s EACLLM in terms of the final solutions obtained, the degree of closeness to the ideal solution, satisfaction degree and the level of conservatism, in addition to guaranteeing the feasibility of the RO formulation. Additionally, the results indicated that in Bertsimas’ EACLLM, the growth in CPU time with increasing scenario size is less than that exhibited by Lin’s EACLLM.

There are several possible extensions to this work that may be interesting lines of future research. These include

• A comparative study between the proposed hybrid solution approach and other solution approaches used to solve multi-objective models under uncertainty.

• Considering the model proposed in this paper under different types of uncertainties and risk.

• Using the model and hybrid solution approach for real-world cases.