Free vibration characteristics of stiffened plates

Abstract

The free vibration characteristics, such as fundamental frequency and mode shape of stiffened plates employing standard finite element analysis, are investigated in this paper. The parametric study is presented for free vibration characteristics of stiffened plates with various parameters, such as type, orientation and number of stiffeners, boundary conditions and aspect ratio of plates and stiffener depth to plate thickness ratio. Typical mode shapes are also presented for clamped square eccentrically stiffened plates. Finally, design charts with non-dimensional parameters are proposed to determine the fundamental frequency of commonly adopted clamped stiffened plates in construction. These charts will be very much useful for designers for obtaining the fundamental frequencies of the stiffened plates of different dimensions without doing much complicated analysis or using standard computer codes.

Introduction

Stiffened plates are extensively used in various engineering structures. The technique of stiffening a plate by providing beams is rather common and it also gives higher value of strength to weight ratio of the structure. This has also made the structure more attractive in practice. Further, these structures are frequently subjected to dynamic loading in their service life. Hence, the dynamic behaviour of stiffened plates is of much interest to the structural engineers. The resonance may occur due to undesirable vibrations due to which the stiffened structure may have sudden failure. It is, therefore, important to know the natural frequencies of these structures accurately. Hence, an in-depth study of free vibration behaviour of these stiffened plates is required to exploit their use. On the other hand, the designers have limited scope and also face difficulty in obtaining the natural frequencies of stiffened plates with conventional techniques. It is also tedious for designers to obtain natural frequencies of the stiffened plates employing numerical tools like finite element method (FEM)/finite difference method (FDM)/other approximate methods. Therefore, a user friendly design chart should be available to the designers for easy and immediate calculation of natural frequencies of stiffened plates of different dimensions.

If the density of stiffeners is very high, the stiffened plate can be analysed using orthotropic plate theory. Kirk (1970) used this approach to evaluate the vibration characteristics of beam plate systems. On the other hand, when the density of the stiffeners is low, an approximate method has to be employed, since the governing differential equations for this case are very cumbersome to solve. Aksu and Ali (1976) used FDM for the vibration analysis of rectangular plate having single stiffener and obtained good results. Other approximate analyses of stiffened plate structures like grillage and finite strip methods were presented by Balendra and Shanmugam (1985) and Filiatrault et al. (1990), respectively. A survey of the earlier works on the vibration analysis of stiffened plates was reported by Mukherjee and Mukhopadhyay (1986) and Mukhopadhyay and Mukherjee (1989). The free and forced vibration responses of square clamped plate were studied by Dharaneepathy and Sudhesh (1990) with different stiffener patterns to obtain an optimal layout of the stiffeners for a given mass subjected to blast loads.

The FEM is the most successful tool used for vibration analysis of plates having discrete stiffeners. A number of research works were carried out by several investigators (Olson and Hazell 1977; Gupta et al. 1986; Mukherjee and Mukhopadhyay 1988; Koko and Olson 1992; Palani et al. 1993; Harik and Guo 1993; Chen et al. 1994; Holopainen 1995) for free vibration study of stiffened plates employing FEM. Further, the vibration analysis of stiffened plates was studied by Barrette et al. (2000) using hierarchical finite elements. Barik and Mukhopadhyay (2002) presented a new four node stiffened plate element to include arbitrary shaped plates without shear locking phenomena. The vibration, buckling and dynamic instability of stiffened plates subjected to in-plane partial and concentrated edge loading were investigated by Srivastav et al. (2003a, b) employing FEM. The results show that the stiffened plate is less susceptible to bucking for the position of loading near the supported edges as well as near the position of stiffeners. Moreover, the location, size and number of stiffeners have a significant effect on the location of the boundaries of the principal instability region. Akl et al. (2008) optimised the static and dynamic characteristics of plate stiffener assembly by taking the orientation angles of stiffeners arranged in the form of iso-grid configuration over a flat plate. Vörös (2009) presented a new stiffener element with 7 degrees of freedom per node considering the stiffener and the plate as separate elements. The vibration analysis of stiffened plates was made by Hamedani et al. (2012) employing both conventional and super finite element methods. Srivastava et al. (2004, 2005, 2013) and Srivastava (2012) investigated vibration characteristics of stiffened plates with cut-outs subjected to in-plane uniform and partial edge loadings at the plate boundaries using FEM. These studies show that aspect ratio of the plate, position and number of stiffeners, and size of cut-outs have pronounced effects on the dynamic instability characteristics in comparison to unstiffened plate.

On the other hand, Nguyen-Thoi et al. (2013) developed a cell-based smoothed discrete shear gap method (CS-FEM-DSG3) using triangular elements to study the free vibration and buckling characteristics of eccentrically stiffened plates. Huang et al. (2015) also developed a finite element model for buckling analysis of grid stiffened laminated composite plates using 6-noded triangular curve shell element based on three-dimensional degenerated shell theory and a compatible 3-noded curved beam element based on a similar hypothesis for the modelling of the stiffeners. It was found from the study that the performance of the model is very good for the problems related to grid stiffened plates with ortho-grid, x-grid, bi-grid and iso-grid stiffening arrangements. A procedure for the vibration analysis of stiffened panels with arbitrary edge constraints was presented by Cho et al. (2015). It is based on the assumed mode method, where natural frequencies and modes are determined by solving an eigen value problem of a multi-degree of freedom system matrix equation derived using Lagrange’s equations of motion. Shi et al. (2015) developed a element method-based approach to study the static, vibration, and buckling characteristics of curvilinear stiffened plates in the presence of in-plane compressive and tensile stresses using the first-order shear deformation theory for both plate and the Timoshenko beam modelling. Rajanna et al. (2016) studied the influence of uniaxial and biaxial partial edge loads on buckling and vibration characteristics of stiffened laminated plates employing finite element method.

From the above discussion, it is evident that most of the researchers have attempted to develop models employing various methods to study static, vibration, buckling and dynamic instability of stiffened plates. There is limited research work focusing on the extensive parametric study of stiffened plates to obtain the effects of various parameters on their static, vibration, buckling and dynamic stability characteristics. Moreover, the user friendly design charts are yet to be developed which will be useful to the designers in obtaining these characteristics of the stiffened plates directly without using any complicated method available in the literature.

To fulfil the some of the lacunae mentioned above, this paper presents the extensive parametric study for free vibration characteristics of stiffened plate, such as fundamental frequency and mode shapes, by developing finite element code as per Nayak and Bandyopadhyay (2002). Then, design charts with non-dimensional parameters are proposed using the computer code based on the present finite element formulation, which will be very much useful to the designers in the practice. Finally, the frequencies of different physical problems of stiffened plates obtained from the proposed design charts and those obtained from the present code are also compared for verifying the accuracy in the design charts.

Mathematical formulation

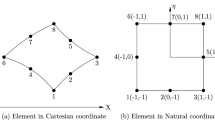
The present formulation of the stiffened plate has been modified by omitting the curvature in the formulation of the stiffened shells developed by Nayak and Bandyopadhyay (2002). Accordingly, the nine node isoparametric plate element and three node beam elements are appropriately combined together to get the stiffness and mass matrices of the stiffened plate element. The plate element has five degrees of freedom, u, v, w, α and β. Here, u, v and w are displacements along x, y and z axes, respectively, and α and β are the rotations along x and y axes, respectively. Considering the first-order shear deformation theory of thin plates in the formulation, the strain–displacement relation is expressed as follows:

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } & {\varepsilon_{y}^{0} } & {\gamma_{xy}^{0} } & {\kappa_{x} } & {\kappa_{y} } & {\kappa_{xy} } & {\gamma_{xz}^{0} } & {\gamma_{yz}^{0} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {\left( {\frac{\partial u}{\partial x}} \right)} & {\left( {\frac{\partial v}{\partial y}} \right)} & {\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)} & {\left( {\frac{\partial \alpha }{\partial x}} \right)} & {\left( {\frac{\partial \beta }{\partial y}} \right)} & {\left( {\frac{\partial \alpha }{\partial y} + \frac{\partial \beta }{\partial x}} \right)} & {\left( {\alpha + \frac{\partial w}{\partial x}} \right)} & {\left( {\beta + \frac{\partial w}{\partial y}} \right)} \\ \end{array} } \right]^{T}$$

(1)

where $\varepsilon_{x}^{0} ,\;\varepsilon_{y}^{0} ,\;\gamma_{xy}^{0} ,\;\gamma_{xz}^{0} \;{\text{and}}\;\gamma_{yz}^{0}$ are usual mid surface strains and $\kappa_{x} ,\;\kappa_{y} \;{\text{and}}\;\kappa_{xy}$ are usual curvatures of the plate element.

The element stiffness and mass matrices of the plate element are derived following the procedure mentioned in Nayak and Bandyopadhyay (2002).

The beam elements considered for stiffeners have four degrees of freedom, i.e., u_sx, w_sx, α_sx and β_sx for the x-directional stiffener and v_sy, w_sy, α_sy and β_sy for the y-directional stiffener. The strain displacement relations for both the stiffener elements are given below:

$$\left\{ {\varepsilon^{\text{sx}} } \right\} = \left[ {\begin{array}{*{20}c} {u_{{{\text{sx}},x}} } & {\alpha_{{{\text{sx}},x}} } & {\beta_{{{\text{sx}},x}} } & {(\alpha_{\text{sx}} + w_{{{\text{sx}},x}} )} \\ \end{array} } \right]^{{{\kern 1pt} {\text{T}}}} \;{\text{for}}\;x{\text{ - direction}}\;{\text{stiffener}}$$

(2)

$$\left\{ {\varepsilon^{\text{sy}} } \right\} = \left[ {v_{{{\text{sy}},y}} \quad \alpha_{{{\text{sy}},y}} \quad \beta_{{{\text{sy}},y}} \quad (\alpha_{\text{sy}} + w_{{{\text{sy}},y}} )} \right]^{{{\kern 1pt} {\text{T}}}} \;{\text{for}}\;y{\text{ - direction}}\;{\text{stiffener}}$$

(3)

Here, $\varepsilon^{\text{sx}} \;{\text{and}}\;\varepsilon^{\text{sy}}$ are strain matrices for x- and y-directional stiffeners, respectively, and comma (,) denotes for differentiation.

Employing the procedure available in the literature (Nayak and Bandyopadhyay 2002), the stiffness and mass matrices of x- and y-direction stiffeners are obtained. Finally, the stiffness and mass matrices of the plate element are obtained as follows:

$$\left[ {{\kern 1pt} K_{\text{e}} } \right] = \left[ {{\kern 1pt} K_{\text{pe}} } \right] + \left[ {{\kern 1pt} K_{\text{xe}} } \right] + \left[ {{\kern 1pt} K_{\text{ye}} } \right]$$

(4)

$$\left[ {{\kern 1pt} M_{\text{e}} } \right] = \left[ {{\kern 1pt} M_{\text{pe}} } \right] + \left[ {{\kern 1pt} M_{\text{xe}} } \right] + \left[ {{\kern 1pt} M_{\text{ye}} } \right]$$

(5)

where [K_e], [K_pe],[K_xe] and [K_ye] are stiffness matrices of stiffened plate, unstiffened plate, x-directional stiffener and y-directional stiffener elements, respectively. Similarly, [M_e], [M_pe], [M_xe] and [M_ye] are mass matrices of stiffened plate, unstiffened plate, x-directional stiffener and y-directional stiffener elements, respectively.

Thereafter, these matrices are assembled to get overall stiffness [K] and mass [M] matrices of the stiffened plate. The equation of free vibration without damping is expressed in the form of Eigen value problem as follows:

$$\left( {\left[ K \right] - \omega^{2} \left[ M \right]} \right)\left\{ d \right\} = \left\{ 0 \right\}$$

(6)

where ω and {d} are Eigen values (natural frequencies) and corresponding Eigen vector (mode shape) of the stiffened plate. The subspace iteration method is used to determine the natural frequencies and corresponding mode shapes of the stiffened plates.

Numerical results and discussions

Convergence study

The convergence study of the present finite element code has been studied with respect to the element mesh size for the square plate with central stiffener (Fig. 1) available in the literature (Olson and Hazell 1977; Koko and Olson 1992; Hamedani et al. 2012). The non-dimensional fundamental frequencies $[\varpi = \omega b^{2} \{ 12\rho (1 - \nu^{2} )/(Eh^{2} )\}^{1/2} ]{\kern 1pt}$ of the above study are presented in Fig. 2 for both simply supported (SS) and clamped (CC) boundary conditions. The element mesh size is made finer till the desired results do not change by more than 1% with further refinement of the grid. It is observed that the non-dimensional fundamental frequencies of the above problem converge to nearly the same value. It is found that 6 × 6 mesh size and 8 × 8 mesh size are required to obtain the converged results of the non-dimensional fundamental frequencies of the above problem for simply supported and clamped boundary conditions, respectively. These two element mesh sizes are further considered to obtain the converged fundamental frequencies of the stiffened plates with simply supported and clamped boundary conditions.

Fig. 1

Square clamped plate with one central stiffener

Fig. 2

Convergence study of stiffened plate elements for the square plate with central stiffener (Fig. 1) available in the literature (Olson and Hazell 1977; Koko and Olson 1992; Hamedani et al. 2012)

Validation of FEM code

The present FEM code is validated by comparing the present free vibration results with those of specific problems available in the literature. The results of the natural frequencies of a square clamped plate with one central stiffener along y-direction (Fig. 1) available in the literature (Olson and Hazell 1977; Koko and Olson 1992; Hamedani et al. 2012) are presented in Table 1 along with those obtained from the present FEM code. Similarly, the results of the natural frequencies for a square clamped plate stiffened with equally spaced two number of stiffeners along y-direction (Fig. 3), obtained from the present code, are also furnished in Table 2 with those obtained by Olson and Hazell (1977), Mukherjee and Mukhopadhyay (1988), Harik and Guo (1993), Chen et al. (1994), Hamedani et al. (2012) and Bhimaraddi et al. (1989). From Tables 1 and 2, it is found that there is good agreement between the present results and those available in the literature and hence the accuracy of the present FEM code is established.

Table 1 Natural frequencies (Hz) of square clamped plate stiffened with one central stiffener (Fig. 1)

Fig. 3

Square clamped plate with two stiffeners along y-direction

Table 2 Natural frequencies (Hz) of square clamped plate stiffened with double stiffeners (Fig. 3)

Parametric study

Several examples of stiffened plates are considered to study the influence on the fundamental frequency with respect to type, orientation and number of stiffeners, boundary conditions and aspect ratio of plates, and stiffener depth to plate thickness ratio. Thereafter, the influence of stiffeners on mode shapes has also been studied. Finally, typical design charts of clamped plates with cross-stiffeners in non-dimensional form are also presented which can be used by the designers to find the fundamental frequency of the stiffened plates directly from the charts.

Types, orientations and numbers of stiffeners

To study the influence of number, types and orientations of stiffeners on square and rectangular clamped stiffened plates, the non-dimensional parameters considered here are as follows:

$$a/b = 1.0,\;1.5,\;{\text{and}}\;2.0;\quad b/h = 200;\quad d_{\text{st}} /h = 5,\quad b_{\text{st}} /h = 1.5\;{\text{and}}\;n = 0.15$$

where a, b and h are length, breadth and thickness of the plate, respectively, b_st and d_st are breadth and depth of stiffeners, respectively, and ν is Poisson’s ratio of the material.

The non-dimensional fundamental frequency of the stiffened plate, $\varpi$, is expressed as follows:

$$\varpi {\kern 1pt} \, = \,\omega \,b^{2} \,\left[ {\frac{{12\,\rho \,\left( {1 - \nu^{2} } \right)}}{{E\,h^{2} }}} \right]^{{\frac{1}{2}\quad }}$$

(7)

where a, b, h, b_st, d_st, ν and ω are defined earlier. E and ρ are Young’s modulus and density of the stiffened plate, respectively.

The values of $\varpi \;$ of stiffened plates have been obtained for various types of stiffeners, i.e., concentric and eccentric, different orientations, i.e., along x-/y-/both x- and y-directions and for increasing number of stiffeners, i.e., 0–10 numbers which are presented in Figs. 4, 5 and 6 for clamped stiffened plates with aspect ratios of 1.0, 1.5 and 2.0, respectively. In case of the plates, other than the square plates, x-directional stiffeners are considered as the stiffeners placed along the longer span while the y-directional stiffeners are considered as the stiffeners placed along the shorter span of the plate.

Fig. 4

Variation of non-dimensional fundamental frequency of a clamped stiffened plate of a/b = 1.0 with different types of stiffeners along different orientations

Fig. 5

Variation of non-dimensional fundamental frequency of a clamped stiffened plate of a/b = 1.5 with different types of stiffeners along different orientations

Fig. 6

Variation of non-dimensional fundamental frequency of a clamped stiffened plate of a/b = 2.0 with different types of stiffeners along different orientations different orientation

From Figs. 4, 5, 6, it is clearly seen that the values of ϖ of clamped stiffened plates increase with the addition of number of stiffeners. This increase is considerable at the early stage with stiffeners of all orientations and types of stiffeners. However, it becomes insignificant gradually after a specific number of stiffeners. It is worthy to mention that further addition of stiffeners may also reduce the fundamental frequency of stiffened plates as observed in Figs. 4, 5, 6 for nine number of stiffeners along x-, y-, and both x- and y-orientations. Both stiffness and mass of the stiffened plates influence the natural frequencies in an interactive manner as expressed in Eq. (6). The addition of stiffeners to the plate increases both mass and stiffness. In some cases, the extra mass due to addition of stiffeners influences more on the natural frequencies than the additional stiffness developed so that the fundamental frequency of the stiffened plates decreases.

Figures 4, 5 and 6 reveal that the eccentric stiffeners in any orientation are showing superior performance in increasing the values of ϖ of clamped stiffened plates in comparison to that of the concentric ones. This may be due to the fact that the first and second moments of area of the stiffeners of plates stiffened with eccentric stiffeners are more than those with concentric stiffeners because of eccentricity of the stiffeners. Therefore, the stiffness of the stiffened plates increases without increase of eccentricity. The eccentric at top and bottom stiffeners has yielded the same result ofϖ.

To compare the performance of plates stiffened with eccentric stiffeners in different orientations, various problems of eccentrically stiffened plates with aspect ratio (a/b) of 1, 1.5 and 2 are considered keeping other non-dimensional parameters constant. The percentage of increase in ϖ of stiffened plates with respect to that of unstiffened plate of same dimension has been obtained and furnished in Table 3. This table reveals that for the aspect ratio 1, the cross-stiffened plates show superior performance to the stiffened plates with equal number of stiffeners along other two orientations with respect to percentage increase in fundamental frequency due to addition of stiffeners. For example, cross-stiffened plates with n_x × n_y = 1 × 1 or 2 × 2 or 3 × 3 have higher ϖ than stiffened plates with n_x or n_y equals to 2 or 4 or 6, respectively. Here, n_x, n_y and n_x x n_y are number of stiffeners along x-, y- and both x- and y-directions, respectively. For aspect ratios 1.5 and 2, stiffened plates with eccentric stiffeners along x-direction show poor performance in comparison to other two orientations. Further, 1 × 1 cross-stiffened plate shows better performance than the y-directional stiffened plate with two numbers of stiffeners. When the number of stiffeners increases, y-directional stiffened plates have higher increase in fundamental frequency than the cross-stiffened plates with equal number of stiffeners.

Table 3 Comparison of increase in percentage of non-dimensional fundamental frequencies of stiffened plate of various dimensions with stiffeners along different directions with the fundamental frequencies of unstiffened plates

The above discussion clearly establishes the better performance of the orthogonal stiffeners for square stiffened plates and the y-directional stiffeners (stiffeners along short span) for rectangular stiffened plates. Hence, other parametric studies are taken up for both orthogonal and y-directional stiffeners.

Boundary condition and aspect ratio

The non-dimensional fundamental frequencies (ϖ) for rectangular and square stiffened plates are obtained for both simple supported and clamped boundary conditions for three different aspect ratios (a/b), i.e., 1, 1.5 and 2 and presented in Figs. 7 and 8 for orthogonal and y-directional stiffeners, respectively.

Fig. 7

Variation of non-dimensional fundamental frequency of eccentrically cross-stiffened plate with respect to boundary conditions and aspect ratios [CC clamped, SS simply supported]

Fig. 8

Variation of non-dimensional fundamental frequency of eccentrically y-directional stiffened plate with respect to boundary conditions and aspect ratios [CC clamped, SS simply supported]

The values of ϖ shown in Figs. 7 and 8 clearly establish the superiority of clamped plates when compared to the simply supported ones for different aspect ratios and for any particular number of stiffeners considered here with two different orientations (i.e., along y- and both x- and y-directions). For such clamped plates, the preference of the aspect ratio is 1.0, 1.5 and 2.0 for higher enhancement of fundamental frequency. It is evident from the above figures that for the same aspect ratio, the value of ϖ in case of simply supported boundary conditions is much less than that of the same number of stiffeners placed on the clamped plates. Hence, the clamped plates are preferred over the simply supported plates with/without placing any number of stiffeners with any type of orientation. Comparing the aspect ratios, it is observed that the square plates with aspect ratio 1 are more efficient than the rectangular plates having aspect ratios 1.5 and 2.0. Hence, the non-dimensional fundamental frequencies (ϖ) decrease with the increase in aspect ratios.

Stiffener depth to plate thickness ratio

As mentioned earlier, the y-directional stiffeners are provided along the shorter span of the plate while x-directional stiffeners are provided along the longer span of the plate. Further, it is found from the study that the plate stiffened along the shorter span shows superior performance with respect to ϖ in comparison to the plate stiffened along the longer span. Hence, the non-dimensional fundamental frequencies (ϖ) for rectangular and square stiffened clamped plates are obtained for different values of stiffener depth to plate thickness ratios (d_st/h) for increasing number of eccentric stiffeners along y-direction and presented in Figs. 9, 10, 11 for aspect ratios 1, 1.5 and 2.0, respectively. From the figures, it is clearly seen that, for a specific plate thickness, the depth of stiffeners does not have significant role particularly for lower number of stiffeners. However, with increasing number of stiffeners, the depth of stiffeners plays an important role. It is also evident from the figures that the increase ofϖ, though appreciable initially with the increase of the number of stiffeners, is not significant with the further increase after 8 number of stiffeners. It is also seen that the value of ϖ decreases with further increase of the number of stiffeners beyond 8 due to the same reason as discussed in the previous section.

Fig. 9

Variation of non-dimensional fundamental frequency of clamped plate (a/b = 1.0) stiffened with eccentric y-directional stiffeners with stiffener depth to plate thickness ratio of plate

Fig. 10

Variation of non-dimensional fundamental frequency of clamped plate (a/b = 1.5) stiffened with eccentric y-directional stiffeners with stiffener depth to plate thickness ratio of plate

Fig. 11

Variation of non-dimensional fundamental frequency of clamped plate (a/b = 2.0) stiffened with eccentric y-directional stiffeners with stiffener depth to plate thickness ratio of plate

Further, it is found that ϖ increases initially with the increase in d_st/h up to certain value of d_st/h and thereafter, there is marginal or no increase in ϖ with further increase of d_st/h. However, ϖ increases with further increase in d_st/h, if the number of stiffeners is increased. The above figures are useful in deciding the corresponding depth of stiffeners for a specific and thickness of the plate. Moreover, for specific values of both d_st and h, the optimum number of stiffeners can be determined in order to attain the desired value of ϖ, if any.

Mode shapes

To study the influence of stiffeners on the mode shapes of clamped plates with different number and orientation of stiffeners at equal spacing, eccentric stiffeners are taken with two different values of the stiffener depth to plate thickness ratio. One value of d_st/h is taken in lower range, i.e., 2 and other value is taken in higher range, i.e., 10 to observe the influence of stiffeners on mode shapes and the corresponding fundamental frequency. The above stiffened plates have the following dimensions:

$$a/b = 1,\quad b/h = 100,\quad b_{\text{st}} /h = 2,\quad d_{\text{st}} /h = 2\;{\text{and}}\;10\,,\quad b = 20.0 \,{\text{m}}, \quad \nu = 0.15,\quad \rho = 2500\,{\text{kg}}/{\text{m}}^{3} ,\quad E = 22.36\,{\text{GPa}}\;{\text{and}}\;\varpi {\kern 1pt} \, = \left[ {wb^{2} \{ 12\rho(1 - \nu^{2} )/\left( {Eh^{2} } \right)\}^{1/2} } \right]$$

Mode shape for the first mode of vibration of clamped square plate without stiffener is prepared and presented in Fig. 12. It is worth mentioning that the variation of fundamental frequency has been studied for the plates stiffened with number of stiffeners 1–10 in each direction, i.e., in x-, y- and x- and y-directions, which gives 30 cases. In order to make this paper compact by avoiding repeating trends, out of 30 cases, only 9 typical cases are considered to study the behaviour of mode shape with lower range of d_st/h = 2 and higher range of d_st/h = 10. The mode shapes of clamped square stiffened plate having d_st/h values of 2 and 10 are plotted for these typical cases and are furnished in Figs. 13 and 14, respectively.

Fig. 12

Mode shape for first mode of vibration of clamped square plate without stiffeners

Fig. 13

First mode of vibration of square clamped plates with varying number and orientation of stiffeners having d_st/h = 2

Fig. 14

First mode of vibration of square clamped plates with varying number and orientation of stiffeners having d_st/h = 10

For unstiffened plate, symmetric modes of vibration (one half sine curve) are seen along both x- and y-axes (Fig. 12) with maximum displacements along the central lines parallel to x- and y-axes. The mode shapes for nine cases of clamped stiffened square plate with varying number and orientations of stiffeners having d_st/h equal to 2, i.e., with one x-directional, one x-directional and one y-directional, two x-directional, two x-directional and two y-directional, three x-directional, three x-directional and three y-directional, five x-directional, five x-directional and five y-directional, and ten x-directional and ten y-directional stiffeners are presented in Fig. 13a–i. The mode shapes of all the above stiffened plates are similar to that of unstiffened plate, i.e., symmetric (one half sine curve) modes of vibration along both axes. The effect of stiffeners is not seen on the mode shapes of the above stiffened plates though there is significant enhancement of the fundamental frequency of these plates due to addition of stiffeners (31–115%) in comparison with that of unstiffened plate (Fig. 13a–i). On the other hand, the mode shapes of the above nine stiffened plates having d_st/h equal to 10 show different trend as shown in Fig. 14. It is worth mentioning that the mode shapes of the stiffened plates with one x-directional, one x-directional and one y-directional, two x-directional, two x-directional and two y-directional, three x-directional and three x-directional and three y-directional stiffeners having d_st/h equal to 10 show complete different pattern of mode shapes in comparison to that of unstiffened plate and the enhancement of the fundamental frequency varies from 126 to 667% due to the addition of stiffeners. Thus, the effects of stiffeners are clearly observed on the mode shapes of these plates (Fig. 14a–f). The plate stiffened with one central stiffener along x-direction produces symmetric mode (one half sine curve) and anti-symmetric mode (two half sine curves) along x- and y-directions, respectively, and increase in fundamental frequency is more than 126% (Fig. 14a). Similarly for other cases, different mode shape patterns are produced. However, these plates with higher number of stiffeners, i.e., with five x-directional, five x-directional and five y-directional and ten x-directional and ten y-directional stiffeners having d_st/h equal to 10, as shown in Fig. 14g–i show the same pattern as in case of the unstiffened one and the presence of stiffeners is not visible on the mode shapes of these stiffened plates though there is very significant enhancement in the fundamental frequency (up to 667%).

From the above results of the mode shape, it is inferred that the stiffened plate having any number and orientation of stiffeners at equal spacing, and lower d_st/h such as 2 behaves as equivalent plate of higher thickness and produces the same mode shape as in case of unstiffened one (Figs. 12, 13). However, the stiffened plate having less number of stiffeners, i.e., up to three numbers in any orientation, and higher d_st/h, such as 10, produces different mode shape indicating the clear presence of stiffeners (Figs. 12, 14). On the other hand, when the stiffeners having higher d_st/h are closely spaced, i.e., more numbers of stiffeners such as five or more are provided with higher d_st/h in any orientation, the stiffened plate also behaves like an equivalent plate of higher thickness and produces the same mode shape as produced in the plate without stiffeners (Figs. 12, 14). In all the above cases, the fundamental frequency of the stiffened plate is higher than that of unstiffened one (Figs. 12, 13, 14).

Design charts for clamped stiffened plates

To propose design charts, a number of clamped stiffened plates of commonly adopted dimensions with cross-stiffeners having eccentricity at bottom with various combinations of the non-dimensional parameters are considered to obtain the non-dimensional fundamental frequency [ϖ = ωb²{12ρ(1 − ν²)/(Eh²)}^1/2]. The constant non-dimensional parameters are b_st/h and ν which are taken as 2.0 and 0.15, respectively. The varying non-dimensional parameters are a/b assigned with values of 1.0, 1.5 and 2.0 and b/h with values of 100, 200 and 300 to include the varying range of thickness of plate and span of plate from practical consideration. The non-dimensional fundamental frequencies (ϖ) are obtained for these problems for d_st/h ratio up to 10. Figures 15, 16, 17, 18, 19, 20, 21, 22, and 23 show the values of the non-dimensional fundamental frequency (ϖ) for these problems.

Fig. 15

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-I)

Fig. 16

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-II)

Fig. 17

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-III)

Fig. 18

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-IV)

Fig. 19

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-V)

Fig. 20

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-VI)

Fig. 21

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-VII)

Fig. 22

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-VIII)

Fig. 23

Variation of the non-dimensional fundamental frequency of eccentric cross-stiffened clamped plate with stiffener depth to plate thickness ratio (case-IX)

The usefulness of Figs. 15, 16, 17, 18, 19, 20, 21, 22, 23 is established by selecting six typical problems of clamped stiffened plates with eccentric cross-stiffeners at bottom. The plates taken up are made of three isotropic materials, such as concrete (four examples having different modulus of elasticity, density and Poisson’s ratio), steel (one example) and aluminium (one example). The plate parameters such as, a, b, h, d_st and n_x, n_y are chosen from practical consideration to cover commonly adopted dimensions of such plates and indicated in Table 4. The values of b_st/h for all examples are kept constant that is equal to 2.0. At first, the dimension parameters of the given practical examples are converted to non-dimensional parameters. The values of ϖ are obtained directly from the design charts (Figs. 15, 16, 17, 18, 19, 20, 21, 22, 23) with linear interpolation for these plates of these non-dimensional values of a/b, b/h, d_st/h and (n_x, n_y) without using the present mathematical formulation. Then, the fundamental frequency (ω) of these example is obtained from the corresponding non-dimensional fundamental frequency (ϖ) by putting the values of the dimension parameters of these stiffened plates in the relation ϖ = ωb²{12ρ(1 − ν²)/(Eh²)}^1/2. Further, the fundamental frequencies of these examples are obtained from the present code using present mathematical formulation. The fundamental frequencies of these examples obtained from both the sources are presented in Tables 4 along with the percentage of deviations between these two sets of results. It is found that the above percentages of deviation are within 6%, which are acceptable for engineering point of view. It is worth mentioning that though the design charts are prepared for the concrete material having Poisson’s ratio as 0.15, the fundamental frequency of other materials such as steel and aluminium having Poisson’s ratio as 0.3 and 0.33, respectively, has been obtained from these charts limiting to the error within 6%. It is worth mentioning that since the design charts (Figs. 15, 16, 17, 18, 19, 20, 21, 22, 23) are presented in non-dimensional form and the non-dimensional fundamental frequency can be obtained from these charts for the stiffened clamped plates of any dimension and material properties. Therefore, the fundamental frequency of the plate can be found out using the dimensions and material properties using the relation mentioned above. Therefore, Figs. 15, 16, 17, 18, 19, 20, 21, 22 and 23 can be used as design charts by the designers to determine the fundamental frequency for clamped stiffened plates of different isotropic materials easily without the help of any computer code or any cumbersome computations. Hence, the above charts (Figs. 15, 16, 17, 18, 19, 20, 21, 22 and 23) are recommended as “Design-aids” for the use in the design of clamped stiffened plates of any isotropic material. Similar design charts can be prepared for other boundary conditions, such as simply supported and cantilever, and for stiffened plates of other orientations, such as x- and y-directional stiffeners. Similarly, the design charts can also be prepared for different b_st/h and, hence, the values of b_st can be chosen suitably by linear interpolation as per the requirement of the designers.

Table 4 Fundamental frequencies (ω) of clamped plates with eccentric cross-stiffeners obtained from the design charts and computer code

Conclusions

Free vibration characteristics, such as fundamental frequency and mode shapes, of stiffened plate are investigated to study the effect of stiffeners employing standard finite element method. Moreover, design charts with non-dimensional parameters are also proposed which will be used by the designers in practice. From the above study, following conclusions are made:

The study of the effects of aspect ratio on the fundamental frequency leads to infer that the increase of the fundamental frequency is maximum for the square plate (a/b = 1) followed by the rectangular and long and narrow plates (a/b = 1.5 and 2) considering the value of ϖ for both simply supported and clamped boundary condition. The clamped boundary condition, however, shows its superiority to the simply supported one for the free vibration behaviour of the stiffened plates.

The fundamental frequency increases with the increase in number of stiffeners. However, the rate of increase of the fundamental frequency, though considerable at the early stage, gradually diminishes with the increase of the number of stiffeners beyond some specific number depending on the plate form and orientations, type and depth to thickness ratio of the stiffeners. At higher number of stiffeners, fundamental frequency may decrease with further addition of stiffeners.

The clamped square plate with cross-stiffeners is seen to be superior to that with equal number of stiffeners along x- or y-direction. However, in rectangular clamped square plate, cross-stiffeners with lower number of stiffeners and y-directional stiffeners with higher numbers show the superior performance in comparison to other two orientations in increasing the fundamental frequency of the clamped stiffened plates.

The detailed study of the effects of the values of d_st/h on the free vibration characteristics reveals that the fundamental frequency increases with increase in the value of d_st/h up to certain value and increase in number of stiffeners up to certain number beyond which there may be marginal increase or no increase or even marginal decrease of fundamental frequency.

The clamped square stiffened plate having any number and orientation of stiffeners at equal spacing, and lower d_st/h, or having more numbers of stiffeners in any orientation and higher d_st/h, behaves as equivalent plate of higher thickness and produces the same mode shape as in case of unstiffened one. However, the stiffened plate having less number of stiffeners and higher d_st/h produces different mode shape indicating the clear presence of stiffeners. In all the cases, the fundamental frequency of the stiffened plate is higher than that of the plate without stiffeners.

The recommended design-aids in non-dimensional parameters (Figs. 15, 16, 17, 18, 19, 20, 21, 22, 23) predict the values of the fundamental frequencies of six typical clamped cross-stiffened plates of different materials, which are fairly close to those obtained from the numerical computation using the computer program (Table 4). These design charts can be used for the designers to determine the fundamental frequency of clamped stiffened plates of any isotropic materials having dimensions from practical consideration.