Introduction

Seismic loading can induce large damages in industrial facilities and their complex components (e.g. Babič and Dolšek 2016; Demartino et al. 2017a, b, c). The loss of the structural integrity of these structures can have severe consequences on the population, the environment and the economy (Krausmann et al. 2010; Rodrigues et al. 2017). Looking at power/chemical/petrochemical plants, storage tank containers are widely employed. These hold liquids, compressed gases or mediums used for the short- or long-term storage of heat or cold. Liquid storage tanks and piping systems are considered as critical components of those industrial facilities (Vathi et al. 2017; Bakalis et al. 2017).

The seismic response of tanks has been widely studied in the past, starting from the pioneering studies of Housner (1957, 1963). In particular, Housner (1957) first presented the simplified formulae to compute the dynamic pressures developed on accelerated liquid containers and successively (Housner 1963) studied the dynamic behavior of ground-supported elevated water tanks considering equivalent spring–mass systems. Current practice for the seismic design of storage tanks is mainly based on Appendix E of API 650 (2007) standard and on Eurocode 8 (1998). Generally speaking, there are many different types of equipment used for the storage of liquids and gases. The characteristics of the different tanks adopted mainly depend on: (a) the quantity of fluid being stored, (b) the nature of the fluid, (c) the physical state of the fluid and (d) the temperature and pressure. In industrial plants, gases are usually stored under high-pressure, often in liquid form since the volume is largely reduced. Spherical storage is preferred for storage of high-pressure fluids. A sphere is usually characterized by even distribution of stresses on the surface and by the smaller surface area per unit volume than any other shapes. These tanks are usually named Horton sphere and are used for storage of compressed gases such as propane, liquefied petroleum gas or butane in a liquid–gas stage.

The seismic analysis of spherical storage tanks requires to account for the fluid–structure interaction and for the soil–structure interaction. The first phenomenon is generated by the presence of a free surface allowing for fluid motions. This phenomenon, referred to as “liquid sloshing”, is generally caused by external tank excitation, and may have a significant influence on the dynamic response (Patkas and Karamanos 2007). The second phenomenon is related to the interaction between the structure and the soil (Mylonakis and Gazetas 2000). In particular, in the case of tanks, EN 1998-4 with reference to foundations on piles, recognizes the importance of kinematic interaction and the effects of dynamic soil–structure interaction.

For spherical pressure vessels, failure modes include steel yielding (possibly leading to plastic collapse) and buckling (elastic or elasto-plastic). Different failure modes exist (e.g., low-cycle fatigue), but yielding and buckling are preeminent. The analysis of the two failure modes is usually done by performing a stress analysis (for yielding) and a stability analysis (for buckling). This paper focuses only on yielding, and shortly deals with buckling. Anyway, for sake of completeness, it should be pointed out that, differently from cylindrical vessels for which different types of buckling can occur under seismic action, directly involving the cylinder (e.g., diamond or elephant foot buckling), in the case of spherical tanks, if provided with a braced lateral load-resisting system, buckling mainly arises in the form of failure of the columns of the supporting system until the vessel becomes unstable (Djermane et al. 2014; Moschonas et al. 2014). With reference to this latter case, Eurocode 3 (2005) classifies cylindrical column sections (which represent the typical cross-section adopted for the supporting system of spherical pressure vessels) in three classes, in relation to the diameter-to-thickness situation ratio. According to this classification, the buckling failure of a column is expected to be caused by local buckling of critical sections for class 2 and 3 sections and by global buckling of the column for class 1 sections.

Although the seismic performance of spherical liquid storage tanks was studied by different authors, little attention has been paid to the assessment of the seismic performances on real cases. Within this framework, the present paper describes an interesting case study concerning the seismic performance of a spherical storage tank containing “butane”. As above underlined, attention is mainly paid to the stress analysis, while the stability analysis is just mentioned since it falls outside the scope of this study. The analysis comprises a sophisticated numerical FE modeling as well as a simplified model for the estimation of the dynamic properties of the tank structure. The paper is organized as follows: First, the steel-spherical pressure vessel containing butane adopted for the case study is presented (Sect. "Case-study"). Sections "Sloshing" and "Soil–structure interaction" describe the mathematical model adopted for accounting for the sloshing and the soil–structure interaction, while Sect. "Fundamental period" focuses on the fundamental period of the structure. Results of the analyses are given in Sect. "Stress analysis" and a parametric analysis is given in Sect. "Sensitivity analysis". Finally, conclusions are given in Sect. "Conclusions".

Case study

The research focuses on a steel-spherical pressure vessel containing pressurized butane (density ρL = 625 kg/m3), with external diameter D = 12.4 m and thickness t = 0.018 m. The sphere is supported by a steel structural system composed of ten circular vertical legs and X-braces. The ten columns are in turn supported by bottom-reinforced concrete (RC) columns. The geometrical and mechanical characteristics of the spherical vessel are summarized in Tables 1 and 2, respectively. The tank is founded on a structural system constituted by a circular beam and piles.

Table 1 Geometrical properties of the spherical vessel
Full size table
Table 2 Mechanical properties of the spherical vessel
Full size table

In the present study, the seismic input is given using the acceleration response spectrum defined according to the Italian code (MIT 2008). The following design conditions are adopted:

  • Nominal expected life of the structure: Vn = 50 years;

  • Utilization coefficient of the structure: 4th class (Cu = 2);

  • Reference period for the seismic action: VR = 100 years;

  • Behavior factor: q = 1.

Seismic zone is identified by the following characteristics: ground type: C; soil type T1 (soil factor S = 1.5).

Seismic hazard parameters of the site are given by:

  • Design ground acceleration for the significant damage requirement (SLV): ag = 0.05 g;

  • Maximum amplification factor of the acceleration response spectrum: F0 = 2.6;

  • Upper period of the constant acceleration branch of the response spectrum: T *C  = 0.5 s.

The above values are representative of low seismicity areas in Italy (Vanzi et al. 2015).

Sloshing

Seismic design provisions of liquid-storage tanks such as API 650 (2007) and Eurocode 8 (1998) are based on a mechanical spring-mass analogy initially developed by Graham and Rodriguez (1952), Jacobsen (1949) and Housner (1963) for rigid tanks and by Haroun and Housner (1982) for flexible tanks.

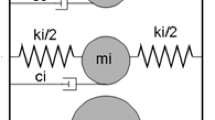
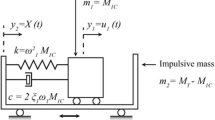
According to this analogy, a tank subjected to a seismic motion may be reduced to a simpler model with lumped masses and springs. More precisely, a portion of the mass of the liquid content (MI) is considered as rigidly connected to the tank walls while the remaining portion (MC) is flexibly attached to the tank walls. The liquid (with mass MI) that synchronizes with the vibration of the tank is called impulsive while the sloshing component of the fluid (with mass MC), generating free surface waves and characterized by its own frequency of vibration, is referred to as the convective component.

In this study, the procedure from Karamanos (2004) is adopted to develop the mechanical spring-mass tank model. For broad tanks, the simplified model reported in Fig. 1 can be applied, where the tank-liquid system is represented by the first impulsive and first convective modes only. In fact, numerical calculations of hydrodynamic forces in horizontal cylinders and spheres showed that, in this case, considering only the first mode may provide a very accurate prediction of the convective and impulsive forces.

Fig. 1
figure 1

Mechanical spring-mass analogy of a liquid-storage tank

Full size image

In Fig. 1, y2 = X (t) represents the motion of the external source, while y1 = u1 (t) expresses the motion of the liquid mass associated to sloshing.

The total mass MT is split into two parts m1 and m2, corresponding to y1 and y2 and expressing the “convective” or “sloshing” motion (M1C) and “impulsive” motion (MI), respectively.

As suggested by Eurocode 8 (1998), the seismic design force FD can be calculated through the SRSS combination of the convective and impulsive maximum values FC,max and FI,max:

$$F_{\text{D}} = \sqrt {\left( {F_{\text{C,max}} } \right)^{2} + \left( {F_{\text{I,max}} } \right)^{2} } .$$
(1)

The maximum convective FC,max and impulsive FI,max forces, neglecting the higher modes of vibration are given by:

$$F_{\text{C,max}} = M_{{ 1 {\text{C}}}} S_{\text{A}} \left( {T_{{ 1 {\text{C}}}} } \right);\quad F_{\text{I,max}} = M_{\text{I}} S_{\text{A}} \left( {T_{\text{I}} } \right);$$
(2)

where SA (T1C) and SA (TI) represent the spectral acceleration calculated in correspondence of the fundamental sloshing and impulsive periods, respectively.

The above quantities can be computed by utilizing the graphs and the tables reported in (Karamanos 2004), which refer to a spherical tank belonging to the same typology of the one herein analyzed. The procedure can be so summarized: (1) calculating the liquid mass ML on the basis of the fluid level in the tank; (2) calculating the total moving mass MT = ML + Mtank, Mtank being the mass of the empty tank; (3) deriving the convective mass M1C from Table 4 in (Karamanos 2004); (4) computing the impulsive mass MI = MT − M1C; (5) obtaining the fundamental sloshing period T1C and the fundamental impulsive period TI from Table 8 in (Karamanos 2004). In the same Table 8 also the maximum convective force FC,max, impulsive force FI,max, and the total design force FD for different liquid levels within the sphere are reported. It can be noted that, since sloshing is a low-frequency motion, the corresponding spectral values are small and as a consequence, the impulsive component of the response prevails. Thus, the maximum seismic design force, i.e., the most unfavorable condition is obtained in corresponding of the maximum possible liquid fill height in the sphere, that is when the fluid mass tends to behave like an impulsive mass and sloshing effects become negligible.

Application to the case study

On the basis of the above considerations, the seismic analysis of the spherical tank object of study was carried out under the most unfavorable hypothesis of maximum seismic force, that is with the sphere filled with butane up to the “block level” equal to 75.5% in height. The 75.5% filling height corresponds to the 85% filling volume. Table 3 shows the deriving values of the involved parameters.

Table 3 Dynamic properties of the spherical tank and seismic forces
Full size table

From Table 3, by comparing the values of FD, FC,max and FI,max, it can be deduced that the convective component of the fluid motion is negligible. Thus, dynamic spectral analyses were carried out by modeling the liquid mass through its impulsive component only. In this way, an accuracy higher than 99% was obtained.

Fundamental period

The fundamental period of the spherical tank was determined by adopting two different approaches:

  1. 1.

    A detailed finite element (FE) model;

  2. 2.

    A simplified methodology based on a single-degree-of-freedom (SDOF) inverted pendulum analogy.

The structure was assumed perfectly constrained at the basis, as it will be better clarified in Sect. "Soil–structure interaction".

As to the first approach (Resta et al. 2013), the tank was modeled by the FE structural analysis code Midas Gen 2017. Different typologies of FEs were used (Fig. 2): (1) plate elements to model the sphere walls and the vertical legs; (2) truss elements to model the X-braces; (3) solid elements to model the foundations and the connections between vertical legs and X-braces.

Fig. 2
figure 2

FE model of the spherical tank

Full size image

The FEM was used to mesh all the components of the tank except for the liquid (butane) which was simulated by masses applied to the sphere nodes. With regard to the mesh size, it is well known that it has a great effect on the accuracy of numerical results. A small mesh size would lead to better results but longer computational time. Thus, it is necessary to find out the suitable mesh size, that for the spherical tank object of study was equal to 0.3 m for plate elements and 0.04 m for solid elements. The mesh size was tightened in correspondence of the sphere-column connections, that were modeled to ensure the node continuity (Fig. 2c). A fundamental period equal to 0.5103 s was so obtained (Fig. 3).

Fig. 3
figure 3

First three modes of vibration of the spherical tank

Full size image

With regard to the second approach, the vessel was assimilated to an inverted pendulum with the mass given by the sum of three contributions: the sphere steel mass, the steel mass of half legs and half X-braces, and the butane mass. The pendulum stiffness can be schematized by a system of springs arranged in series or in parallel (Fig. 4).

Fig. 4
figure 4

SDOF inverted pendulum analogy of the spherical tank

Full size image

More precisely, it was achieved by considering three in series subsystems: the first one is represented by the foundation stiffness (including the contributions of the circular beam and of the piles); the second one is constituted by the stiffness of the bottom RC columns; the third one is given by the stiffness aliquots of the vertical legs and X-braces arranged in parallel. By recalling that the flexibility, f, of a serial system is given by the sum of the component flexibilities and conversely the stiffness, k, of a parallel system is given by the sum of the different stiffness aliquots, it can be written:

$$k = \frac{1}{f} ; \quad f = f_{1} + f_{2} + f_{3 - 4} ; \quad k_{3 - 4} = k_{3} + k_{4}$$
(3)

where f1 is the flexibility of the foundation; f2 is the flexibility of the bottom RC columns; f3–4 and k3–4 are the flexibility and the stiffness of the parallel system constituted by the vertical legs (f3, k3) and the X-braces (f4, k4), respectively.

Since the foundation system is extremely rigid (k1 → ∞), the value of f1 tends to zero; similarly, the value of f2 is rather small, the bottom slabs being very squat structural elements. Thus, the quantities f1 and f2 can be neglected, anyway obtaining an increase of the safety level. In fact, a higher total stiffness k would cause an increase of the fundamental period of the overall system, leading to reduced design spectral values and then to reduced seismic forces. By observing Fig. 4, the following expressions were derived for k3 and k4:

$$k_{3} = 10 \times \frac{{12 \times E_{\text{s}} \times j_{\text{leg}} }}{{H_{\text{leg}}^{ 3} }}; \quad k_{4} = \mathop \sum \limits_{i = 1}^{9} \frac{{E_{\text{s}} A_X{\text{-brace}} }}{{L_X{\text{-brace}} }} \times \left( {\cos \varTheta_{v} } \right)^{2} \cdot \left( {\cos \varTheta_{hi} } \right)^{2} ;$$
(4)

where Θv = 60° and Θhi = (90° − i.36°).

By the described approach a fundamental period equal to 0.519 s was achieved, in perfect accordance with the value obtained through the FE model. It was calculated by the simple expression T = 2π (MI/k); the values of the stiffness parameters are summarized in Table 4.

Table 4 Stiffness parameters of the inverted pendulum model
Full size table

Soil–structure interaction

The analysis of soil–foundation–structure interaction can be carried out by different methods, depending on the part of the system that is examined. These methods can be classified into: (1) analytical, usually referring to simple foundation geometries lying on elastic half-space; (2) semi-analytical, combining analytical formulations for the half-space with numerical procedures; (3) numerical, usually FEM; (4) simplified discrete models, which allow fast calculation of the foundation–soil–structure system properties.

Discrete models for the analysis of soil–foundation–structure system have been developed by various researchers and are the most used for practice purposes. Focusing on pile foundations, according to these methods, the restraining action of soil is simulated by distributed springs and dashpots which substantially result in the evaluation of dynamic impedances for a single pile foundation.

Different formulations can be found in the literature to calculate the dynamic impedances, depending on various parameters among which the frequency of seismic excitation.

The general expression of a dynamic impedance along an arbitrary degree of freedom is given by: k + iΩc, where k and c represent the foundation stiffness and damping, while Ω is the circular excitation frequency.

Gazetas et al. (1993) for the dynamic impedances of a single pile in vertical and lateral directions proposed the following frequency-dependent expressions:

$$k_{z} = 0.6E_{\text{s}} \left( {1 + \frac{1}{2}\sqrt {a_{0} } } \right);$$
(5)
$$c_{z} = 2\xi_{\text{s}} \frac{{k_{z} }}{\varOmega } + \rho_{\text{s}} V_{\text{s}} R\left( {a_{0} } \right)^{ - 1/4} ;$$
(6)
$$k_{x} = 1.2E_{\text{s}} ;$$
(7)
$$c_{x} = 2\xi_{\text{s}} \frac{{k_{x} }}{\varOmega } + 6\rho_{\text{s}} V_{\text{s}} R\left( {a_{0} } \right)^{ - 1/4} ;$$
(8)

where Es is the Young’s modulus of elasticity of soil; ρs is the mass density of soil; ξs is the hysteretic damping coefficient of soil; Vs is the shear wave velocity of soil; R is the radius of the pile transversal section; a0 = Ω R/Vs is a dimensionless frequency parameter.

Gazetas (1984) also proposed approximate expressions not depending on the excitation frequency of soil.

Velestos and Tang (1990), for the calculation of lateral and rocking impedances of a single pile, furnished the following relations:

$$k_{x} = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\alpha_{x} ;$$
(9)
$$c_{x} = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\beta_{x} \frac{R}{{V_{\text{s}} }};$$
(10)
$$k_{\theta } = \frac{{8G_{\text{s}} R^{3} }}{{3\left( {1 - \nu_{\text{s}} } \right)}}\alpha_{\theta } ;$$
(11)
$$c_{\theta } = \frac{{8G_{\text{s}} R^{3} }}{{3\left( {1 - \nu_{\text{s}} } \right)}}\beta_{\theta } \frac{R}{{V_{\text{s}} }};$$
(12)

where Gs is the shear modulus of elasticity of soil and νs is the Poisson ratio of soil. For νs ~ 1/3, the coefficients α and β are given by:

$$\alpha_{x} = 1;\quad \beta_{x} = 0.65;$$
(13)
$$\alpha_{\theta } = 0.5\frac{{\left( {0.8a_{0} } \right)^{2} }}{{1 + \left( {0.8a_{0} } \right)^{2} }};\quad \beta_{\theta } = 0.4\frac{{\left( {0.8a_{0} } \right)^{2} }}{{1 + \left( {0.8a_{0} } \right)^{2} }}.$$
(14)

Finally, Maravas et al. (2014) proposed the following expressions, not depending from Ω:

$$k_{x} = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\lambda_{x} ;$$
(15)
$$c_{x} = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\chi_{x} \frac{R}{{V_{\text{s}} }};$$
(16)
$$k_{\theta } = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\lambda_{\theta } ;$$
(17)
$$c_{\theta } = \frac{{8G_{\text{s}} R}}{{2 - \nu_{\text{s}} }}\chi_{\theta } \frac{R}{{V_{\text{s}} }}.$$
(18)

The coefficients λ and χ are given by:

$$\lambda_{x} = 1;\quad \chi_{x} = 0.575;$$
(19)
$$\lambda_{\theta } = 0.15;\quad \chi_{\theta } = 0.15.$$
(20)

As to the influence of pile group configuration, in current engineering practice, the dynamic impedances of pile groups are usually estimated using the impedances of a single pile and accounting for the group effect by means of interaction factors (static or dynamic). These group effects, due to the kinematic component of the pile-soil dynamic interaction, are quite small and can be neglected when, as in the case under examination, the ratio Ep/Es (L) between the pile and the soil (at the pile extremity) Young’s moduli of elasticity is \(\ll 1000\) (Gazetas et al. 1993).

Application to the case study

As above underlined, in the proposed study, it is possible to refer to single pile impedances, without accounting for the group effects. With reference to the analyzed spherical pressure vessel, the lateral impedance kx of a single pile was calculated by Eqs. (7), (9) and (15), so obtaining comparable values (~ 571,337.5 N/m). The total number of piles is 40. The period resulting from the simplified model described in Sect. "Fundamental period" is equal to 0.87 s. As a consequence, the consideration of soil–structure interaction would be beneficial in this case, leading to a higher value of natural period and to reduced seismic spectral forces. For this reason, this effect was neglected and the vessel was assumed perfectly constrained at the basis.

Stress analysis

The stress analysis was performed using the FE model of the spherical pressure tank depicted in Sect. "Fundamental period". The following load cases were considered:

  • Dead load (G1);

  • Internal pressure (Pi = 6 bar);

  • Hydrostatic pressure (PH, due to butane);

  • Seismic spectral loads in all three directions.

Verifications were carried out in terms of Von-Mises stresses. The following load combination resulted to be the most unfavorable condition: 1 × G1 + 1 × Pi + 1 × PH − 1 × Seism X − 0.3 × Seism Y + 0.3 × Seism Z.

Figure 5a–d shows the corresponding stress distributions; in particular Fig. 5a focuses on the sphere and the vertical legs, Fig. 5b highlights stresses in the X-braces and Fig. 5c, d reports stresses in connections between vertical legs and X-braces. As it emerges from Table 5, in all elements, stresses are lower than the corresponding design limit strengths, that is the analyzed spherical tank has a good level of safety against seismic action. Displacement diagrams for the same load combination are finally given in Fig. 6.

Fig. 5
figure 5

Stress configuration in correspondence of the most unfavorable seismic load combination (Von-Mises stresses)

Full size image
Table 5 Stress verifications (Von-Mises stresses)
Full size table
Fig. 6
figure 6

Resultant displacements in correspondence of the most unfavorable seismic load combination

Full size image

It is worth to note that global and local buckling phenomena were also checked. For the case study, buckling safety margins were high, and, for the sake of conciseness, buckling verification is not documented in the paper. Global buckling verification was made on legs, under normal stress and bending moment. The compressed brace within each X-brace couple was obviously removed from the FE model since its buckling stress is very low. Local buckling verification was made at the maximum compression stress locations in legs, and at leg-sphere intersection sections. In both cases, local stresses were low and compatible with buckling verifications. It should be noted that this is not a general feature of this type of tanks, and buckling behavior was satisfactory for this case study tank, under the case study seismic action.

Sensitivity analysis

With the aim to analyze the stress–strain configuration of the spherical tank also under different boundary conditions, other three structural schemes were taken into account: (1) the same vessel previously considered but with spherical hinges at the basis (referred to as model B); (2) the same vessel previously considered but without X-braces (referred to as model C); the vessel with spherical hinges at the basis and without X-braces (referred to as model D). The vessel analyzed in previous sections, perfectly constrained at the basis and with X-braces, is referred to as model A. The overall studied models are summarized in Table 6.

Table 6 Structural models considered for the sensitivity analysis
Full size table

The described structural schemes allow examining all the configurations that could affect the spherical tank, due for example to an unexpected seismic event or to a malfunctioning of constraints or so far to the development of a plastic mechanism in the X-braces.

Strength verifications were carried out under the most unfavorable seismic load condition.

The fundamental periods, the maximum stresses and the maximum displacements of the four models are compared in Table 7. It emerges that the fundamental period of the structure increases as boundary constraints decrease. It can be also noted that the extremity release at the basis (model B) produces effects, in terms of fundamental period, similar to the elimination of X-braces (model C), coherently with the reciprocal values of stiffness (Table 4), derived from the simplified model depicted in Sect. "Fundamental period". Maximum stresses are obtained in correspondence of Model A, proving its effectiveness in terms of structural safety.

Table 7 Structural models considered for the sensitivity analysis
Full size table

In all the models, maximum Von-Mises stresses occurred in sphere walls, in the proximity of vertical legs. The sensitivity analysis was aimed at assessing structural safety in case of unexpected behavior of braces and constraints, due to braces and foundation stem yielding. Such behavior could arise for structural properties (e.g., materials; construction details) different from the assumed ones. The analysis showed that the stress level was similar to that computed for model A (the reference one). A further useful result was the estimation of the maximum displacement. This was an important piece of information for verification of the tubes connecting the sphere to the external services. The tubes, in fact, may be torn by displacements incompatible with their flexibility.

Conclusions

In this study, the seismic behavior of a spherical pressure vessel containing butane was analyzed, accounting for the influence of sloshing effects and of the soil–structure interaction. Both a detailed FE model of the spherical tank and a simplified SDOF-inverted pendulum model were implemented. It was shown which are the most unfavorable conditions to be considered under sloshing and soil–structure interaction effects: (1) liquid in the sphere up to the “block level”; (2) structure perfectly constrained at the basis. Structural robustness was also checked: plastic mechanisms in the X-braces or malfunctioning of the base constraints were independently modeled, thus showing structural performance in case of unexpected high (i.e., higher than code design earthquakes) seismic event or malfunctioning of constraints.

In conclusion, a significant case study concerning the seismic behavior of a spherical tank containing butane was presented in this paper. In spite of the limitations due to the uniqueness of the real case object of study, some specific issues dealing with spherical tanks were simultaneously addressed (sloshing, soil–structure interaction, FE modeling), so providing a rational framework for the analysis of such special structures, particularly useful for practical purposes. Whereas the detailed observations may be dependent on the analyzed case study, the broad conclusions, such as the considerations about simplified modeling, sloshing or soil–structure interaction, should apply to many practical cases.