Free vibration analysis of axisymmetric laminated composite circular and annular plates using Chebyshev collocation

Abstract

Solutions, based on principle of collocating the equations of motion at Chebyshev zeroes, are presented for the free vibration analysis of laminated, polar orthotropic, circular and annular plates. The analysis is restricted to axisymmetric free vibration of the plates and employs first-order shear deformation theory for the displacement field, in terms of midplane displacements, u, α and w. The eigenvalue problem is defined in terms of three equations of motion in terms of the radial co-ordinate r, the radial variation of the displacements being represented in polynomial series, with appropriate boundary conditions. Numerical results are presented to show the validity and accuracy of the proposed method. Results of parametric studies for laminated polar orthotropic circular and annular plates with different boundary conditions, orthotropic ratios, lamination sequences, number of layers and shear deformation are also presented.

Introduction

Fiber-reinforced composite structures are often subjected to dynamic loading caused by time-dependent loads causing vibrations or wave propagation. Then, the response of these structures under time-varying loads depends not only on the distribution of the stiffness of material in the structure, but also on the distribution of mass inertia. The analyst has to then consider the effect of inertia forces set up within the structure at any instant. The studies of flexural vibrations of plates subjected to different boundary conditions have thus received considerable interest because of their technological importance, and also give a good idea of response characteristics of the structure under dynamic loads.

Circular and annular plates are commonly used structural components in aerospace, civil, mechanical, electronic and nuclear engineering applications. In industrial situations, it is often required to predict the free vibration characteristics of these plates. For the free vibration analysis of various plates, there are a number of solution techniques, such as analytical methods, energy methods, finite difference methods and finite element methods. Analytical solutions form an important basis for comparison and verification of results obtained by numerical methods such as the finite element method. Among the different m is also the Chebyshev collocation method.

There have been a number of investigations of the free vibration of homogeneous isotropic circular and annular plates such as Han and Liew (1999), Haterbouch and Benamar (2005), Liew et al. (1997), Liew and Yang (1999), Liew and Yang (2000), Selmane and Lakis (1999) and Zhou et al. (2003). There are works employing solutions using differential quadrature and generalized differential quadrature methods for the study of this class of problems and so also a few finite element solutions for the analysis of laminated plates and shells such as Han and Liew (1997), Lin and Tseng (1998), Ding and Xu (2000), Liew and Liu (2000), Wu et al. (2002), Tornabene et al. (2009) and Hosseini-Hashemi et al. (2010). In a recent paper (Xiang et al. 2014), the equations of motion of composite laminated annular plates, conical and cylindrical shells, with various boundary conditions based on the first-order shear deformation theory, have been solved for natural frequencies using an innovative, Haar wavelet discretization method. However, there are not many studies showing use of collocation at Chebyshev zeroes as an effective solution methodology for the determination of natural frequencies of laminated circular and annular plates.

In the present work, it is proposed to study the free vibration characteristics of laminated polar orthotropic circular and annular plates by Chebyshev collocation method. The possible application of orthogonal collocation to boundary value problems has been discussed by Villadsen and Stewart as early as (1967). Carey and Finlayson (1974) have explored the concept of orthogonal collocation in finite element analysis. The method has been used earlier for solving problems of free vibration analysis and large amplitude deflection analysis of isotropic and orthotropic spherical shells—static analysis (Dumir et al. 1984; Nath and Jain 1986). Dumir et al. (2001) have presented geometrically nonlinear analysis of a moderately thick, laminated composite annular plate subjected to uniformly distributed ring loads. Narasimhan (1992) has analyzed the problem of dynamic response analysis of laminated spherical shells using the same method. Herein, the possible application of the methodology for solution of axisymmetric free vibration response of circular and annular (polar) orthotropic plates has been illustrated.

In the present research, the reference plane displacements u, α and w are expanded in polynomial series and then orthogonal point collocation method is used to discretise the governing equations. The eigenvalue problem is derived from the equations of motion, neglecting the rotary inertia and inplane inertia terms. To demonstrate the convergence of the method, numerical results are presented for clamped and simply supported isotropic and polar orthotropic circular and annular plates. The validity of the solution methodology adopted is confirmed by comparing nondimensional frequencies for isotropic and polar orthotropic plates obtained from the proposed solution with data obtained from open literature. It is observed that the present method is efficient in obtaining the free vibration frequencies and mode shapes of the laminated circular and annular plates made of composite materials. Parametric studies are also conducted and it is concluded that free vibration frequencies are dependent not only on the boundary conditions, but also on the parameters such as fiber orientation, lamination sequence and hole diameter.

Methods

Mathematical formulation

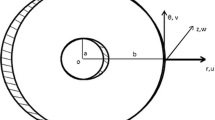
The laminated plate of constant thickness h is composed of polar orthotropic laminae stacked in any arbitrary sequence, but with their fiber reinforcement aligned either in radial or circumferential directions only is considered. Polar co-ordinates (r, θ, z) are used for plate co-ordinates as shown in Fig. 1, where u, v, w denote the displacements of any point of the plate in the corresponding r, θ, z directions.

Fig. 1

Geometry of n-layered laminate

First-order shear deformation theory is employed in the present study and the displacement field is assumed to be of the form

$$ \begin{aligned} u(r,\theta ,z) &= u^{0} (r,\theta ) + z\alpha_{1} (r,\theta ), \hfill \nonumber \\ v(r,\theta ,z) &= v^{0} (r,\theta ) + z\alpha_{2} (r,\theta ), \hfill \nonumber\\ w(r,\theta ,z) &= w^{0} (r,\theta ) \hfill \\ \end{aligned} $$

(1)

where u ⁰, v ⁰, w ⁰ denote the displacements of any point on the middle surface and α ₁, α ₂ are the rotations of the normal to the midplane about θ, r axes, respectively.

The linear strain displacement relations for the general motion of a point on the reference surface of laminated orthotropic circular plates are given by

$$ \varepsilon_{r} = \varepsilon_{r}^{0} + \,z \cdot \kappa_{r} ,\quad \varepsilon_{\theta } = \varepsilon_{\theta }^{0} + z \cdot \kappa_{\theta } ,\quad \gamma_{r\theta } = \gamma_{r\theta }^{0} + z \cdot \kappa_{r\theta } ,\quad \gamma_{rz} = \gamma_{rz}^{0} ,\quad \gamma_{\theta z} = \gamma_{\theta z}^{0} $$

(2)

where the reference surface strains and curvatures are given by

$$ \begin{aligned} \varepsilon_{r}^{0} &= \frac{{\partial u^{0} }}{\partial r}, \quad \varepsilon_{\theta }^{0} = \frac{1}{r} \cdot \left( {\frac{{\partial v^{0} }}{\partial \theta } + u^{0} } \right) \hfill \nonumber \\ \gamma_{r\theta }^{0} &= \frac{1}{r} \cdot \left( {\frac{{\partial u^{0} }}{\partial \theta } - v^{0} } \right) + \frac{{\partial v^{0} }}{\partial r},\nonumber \\ \gamma_{rz}^{0} &= \alpha_{1} + \frac{\partial w}{\partial r},\quad \gamma_{\theta z}^{0} = \alpha_{2} + \frac{1}{r} \cdot \left( {\frac{\partial w}{\partial \theta }} \right) \hfill \nonumber \\ \kappa_{r} &= \frac{{\partial \alpha_{1} }}{\partial r},\quad \kappa_{\theta } = \frac{1}{r} \cdot \left( {\frac{{\partial \alpha_{2} }}{\partial \theta } + \alpha_{1} } \right),\nonumber \\ \kappa_{r\theta } &= \frac{1}{r} \cdot \left( {\frac{{\partial \alpha_{1} }}{\partial \theta } - \alpha_{2} } \right) + \frac{{\partial \alpha_{2} }}{\partial r} \hfill \\ \end{aligned} $$

(3)

According to the shear deformation theory, the constitutive equations for the kth layer of a polar orthotropic laminated plate can be written in the following form in polar co-ordinates

$$ \begin{aligned} & \left\{ \begin{array}{l} \sigma_{r} \hfill \\ \sigma_{\theta } \hfill \\ \tau_{r\theta } \hfill \\ \end{array} \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]^{(k)} \,\,\left\{ \begin{array}{l} \varepsilon_{r} \hfill \\ \varepsilon_{\theta } \hfill \\ \gamma_{r\theta } \hfill \\ \end{array} \right\}^{(k)} ,\\ & \left\{ \begin{array}{l} \tau_{rz} \hfill \\ \tau_{\theta z} \hfill \\ \end{array} \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {C_{44} } & 0 \\ 0 & {C_{55} } \\ \end{array} } \right]^{(k)} \,\,\left\{ \begin{array}{l} \gamma_{rz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{array} \right\}^{(k)} , \end{aligned} $$

(4)

where the elastic constants are expressed in terms of material constants of the lamina in the plate co-ordinates as

$$ \begin{aligned} {C_{11}} &= \frac{{E_{r} }}{{1 - \upsilon_{r\theta } \upsilon_{\theta r} }}\quad {C_{12}} = \frac{{\upsilon_{r\theta } E_{\theta } }}{{1 - \upsilon_{r\theta } \upsilon_{\theta r} }} = \frac{{\upsilon_{\theta r} E_{r} }}{{1 - \upsilon_{r\theta } \upsilon_{\theta r} }} \\ {C_{22}} &= \frac{{E_{\theta } }}{{1 - \upsilon_{r\theta } \upsilon_{\theta r} }} \hfill \\ C_{44} &= \, G_{rz} , \quad C_{55} = \, G_{\theta z} , \quad C_{66} = G_{r\theta } \hfill \\ \end{aligned} $$

(5)

where E _r and E _θ are Young’s moduli of elasticity in r and θ directions. υ _rθ and υ _θr are Poisson’s ratios. G _rθ , G _θz and G _rz are the shear moduli in the respective planes.

The stress resultants acting on a laminate are obtained as:

$$ \begin{aligned} \left[{\begin{array}{lll} {N_{r} } & {M_{r} } \\ {N_{\theta } } & {M_{\theta } } \\ {N_{r\theta } } & {M_{r\theta } } \\ \end{array} } \right] &= \int\limits_{ - h/2}^{h/2} {\left\{ \begin{array}{l} \sigma_{r} \hfill \\ \sigma_{\theta } \hfill \\ \tau_{r\theta } \hfill \\ \end{array} \right\} (1,z) {\text{d}}z} \\ &= \sum\limits_{k = 1}^{n} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \sigma_{r} \hfill \\ \sigma_{\theta } \hfill \\ \tau_{r\theta } \hfill \\ \end{array} \right\}^{(k)} \,(1,} } z)\,{\text{d}}z, \hfill \\ \left\{ \begin{array}{l} Q_{r} \hfill \\ Q_{\theta } \hfill \\ \end{array} \right\} &= K^{2} \,\int\limits_{ - h/2}^{h/2} {\left\{ \begin{array}{l} \tau_{rz} \hfill \\ \tau_{\theta z} \hfill \\ \end{array} \right\}} \,{\text{d}}z = \,K^{2} \,\sum\limits_{k = 1}^{n} {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \tau_{rz} \hfill \\ \tau_{\theta z} \hfill \\ \end{array} \right\}^{(k)} } } {\text{d}}z \hfill \\ \end{aligned} $$

(6)

where z is the distance of the lamina from the middle plane.

The first-order shear deformation theory used herein assumes a constant state of transverse shear strain through the thickness of the plate and hence requires shear correction factors introduced to account for non-uniform distribution of the transverse shear strains through the thickness of the plate. In Eq. (6), K ² is the Shear correction factor introduced to account for non-uniform distribution of the transverse shear strains through the thickness of the plate, which is taken as π ²/12.

Substituting the stress strain relations in the expressions for stress resultants, we have

$$ \begin{aligned} &\left\{ \begin{array}{l} N_{r} \hfill \\ N_{\theta } \hfill \\ N_{r\theta } \hfill \\ \end{array} \right\} = \sum\limits_{k = 1}^{n} {\left[ {\begin{array}{lll} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]^{(k)} \left\{ {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \varepsilon_{r}^{^\circ } \hfill \\ \varepsilon_{\theta }^{^\circ } \hfill \\ \gamma_{r\theta }^{^\circ } \hfill \\ \end{array} \right\}\,{\text{d}}z\,\,\, + \,\,\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \kappa_{r} \hfill \\ \kappa_{\theta } \hfill \\ \kappa_{r\theta } \hfill \\ \end{array} \right\}\,\,z\,{\text{d}}z} } } \right\}} \hfill \nonumber \\ &\left\{ \begin{array}{l} M_{r} \hfill \\ M_{\theta } \hfill \\ M_{r\theta } \hfill \\ \end{array} \right\} = \sum\limits_{k = 1}^{n} {\left[ {\begin{array}{lll} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]}^{(k)} \left\{ {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \varepsilon_{r}^{^\circ } \hfill \\ \varepsilon_{\theta }^{^\circ } \hfill \\ \gamma_{r\theta }^{^\circ } \hfill \\ \end{array} \right\}\,z\,{\text{d}}z + \int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \kappa_{r} \hfill \\ \kappa_{\theta } \hfill \\ \kappa_{r\theta } \hfill \\ \end{array} \right\}\,z^{2} {\text{d}}z} } } \right\} \hfill \nonumber\\ &\left\{ \begin{array}{l} Q_{r} \hfill \\ Q_{\theta } \hfill \\ \end{array} \right\} = \,\,\,K^{2} \,\,\sum\limits_{k = 1}^{n} {\left[ {\begin{array}{ll} {C_{44} } & 0 \\ 0 & {C_{55} } \\ \end{array} } \right]}^{(k)} \left\{ {\int\limits_{{z_{k - 1} }}^{{z_{k} }} {\left\{ \begin{array}{l} \gamma_{rz}^{^\circ } \hfill \\ \gamma_{\theta z}^{^\circ } \hfill \\ \end{array} \right\}\,{\text{d}}z} } \right\}. \hfill \\ \end{aligned} $$

(7)

Since $\varepsilon_{r}^{0} ,\varepsilon_{\theta }^{0} ,\gamma_{r\theta }^{0} ,\kappa_{r} , \, \kappa_{\theta } , \, \kappa_{r\theta } ,\gamma_{rz}^{0} ,\gamma_{\theta z}^{0}$ are middle surface strains and curvatures and not functions of z, they can be taken out of the integration signs. Thus, the total plate constitutive equations can be written as

$$ \left\{ \begin{array}{l} N_{r} \hfill \\ N_{\theta } \hfill \\ N_{r\theta } \hfill \\ M_{r} \hfill \\ M_{\theta } \hfill \\ M_{r\theta } \hfill \\ Q_{r} \hfill \\ Q_{\theta } \hfill \\ \end{array} \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 & 0 & 0 \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 & 0 & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } & 0 & 0 \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 & 0 & 0 \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 & 0 & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {K^{2} A_{44} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {K^{2} A_{55} } \\ \end{array} } \right]\left\{ \begin{array}{l} \varepsilon_{r}^{^\circ } \hfill \\ \varepsilon_{\theta }^{^\circ } \hfill \\ \gamma_{r\theta }^{^\circ } \hfill \\ \kappa_{r} \hfill \\ \kappa_{\theta } \hfill \\ \kappa_{r\theta } \hfill \\ \gamma_{rz}^{^\circ } \hfill \\ \gamma_{\theta z}^{^\circ } \hfill \\ \end{array} \right\} $$

(8)

$$ {\text{where}},\;A_{ij} = \sum\limits_{k = 1}^{n} {(C_{ij} )^{(k)} \left( {z_{k} - z_{k - 1} } \right),} \quad i, \, j = 1, \, 2,6,4,5 $$

$$ B_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{n} {(C_{ij} )^{(k)} } (z_{k}^{2} - z_{k - 1}^{2} ),\quad i, \, j \, = \, 1, \, 2,6 $$

$$ D_{ij} = \frac{1}{3}\sum\limits_{k = 1}^{n} {(C_{ij} )^{(k)} (z_{k}^{3} } - z_{k - 1}^{3} ),\quad i, \, j \, = \, 1, \, 2,6 $$

(9)

A _ij is the extensional stiffness, B _ij is the bending–extension coupling stiffness, D _ij is the bending stiffness.

If the plates are subjected to transverse loads only, the stress resultants and stress couples must satisfy the following equilibrium equations (Ravichandran 1989)

$$ \begin{aligned} &\frac{{\partial N_{r} }}{\partial r} + \frac{1}{r}\frac{{\partial N_{r\theta } }}{\partial \theta } + \frac{{(N_{r} - N_{\theta } )}}{r} = 0,\quad \frac{{\partial Q_{r} }}{\partial r} + \frac{1}{r}\frac{{\partial Q_{\theta } }}{\partial \theta }\,\, + \frac{{Q_{r} }}{r}\,\, = \,\,I_{o} \,\frac{{\partial^{2} w}}{{\partial t^{2} }},\frac{{\partial M_{r} }}{\partial r} + \frac{1}{r}\frac{{\partial M_{r\theta } }}{\partial \theta } + \frac{{(M_{r} - M_{\theta } )}}{r} = Q_{r} \hfill \nonumber \\ & \frac{{\partial N_{r\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial N_{\theta } }}{\partial \theta } + 2\frac{{N_{r\theta } }}{r} = 0,\quad \frac{{\partial M_{r\theta } }}{\partial r} + \frac{1}{r}\frac{{\partial M_{\theta } }}{\partial \theta } + 2\frac{{M_{r\theta } }}{r} = Q_{\theta } \hfill \\ \end{aligned} $$

(10)

$$ {\text{where}}\;I_{0} \, = \,\sum\limits_{k = 1}^{n} {\int\limits_{{h_{k - 1} }}^{{h_{k} }} {\rho^{(k)} \,dz} } = \,\,\rho h\,\,\sum\limits_{k = 1}^{n} {\left\{ {\frac{{\rho^{(k)} }}{\rho h}\,\,\left( {h_{k} \, - \,h_{k - 1} } \right)} \right\}} = \,\rho \,\,h\,R_{m} \, $$

(11)

$$ {\text{where}}\;R_{m} \, = \,\sum\limits_{k = 1}^{n} {\left\{ {\frac{{\rho^{(k)} }}{\rho \,h}\left( {h_{k} \, - \,h_{k - 1} } \right)} \right\}} $$

(11a)

and ρ is a reference density.

For axisymmetric case, the stresses and strains are independent of θ and τ _rθ  = τ _zθ  = 0, v ⁰ = 0, α ₂ = 0 and also $\frac{\partial }{\partial \theta }(\,\,\,)$ = 0. This also leads to N _rθ  = 0, M _rθ  = 0 and Q _θ  = 0.

Substituting for stress resultants and stress couples in Eq. (10) in terms of strains and curvatures which in turn are substituted in terms of displacements given by Eq. (3), the equations take the form

$$ A_{11} \left( {\frac{{\partial^{2} u^{0} }}{{\partial r^{2} }} + \frac{{\partial u^{0} }}{r \cdot \partial r}} \right) - A_{22} \frac{{u^{0} }}{{r^{2} }} + B_{11} \left( {\frac{{\partial^{2} \alpha_{1} }}{{\partial r^{2} }} + \frac{{\partial \alpha_{1} }}{r \cdot \partial r}} \right) - B_{22} \frac{{\alpha_{1} }}{{r^{2} }} = 0 $$

$$ B_{11} \left( {\frac{{\partial^{2} u^{0} }}{{\partial r^{2} }} + \frac{{\partial u^{0} }}{r \cdot \partial r}} \right) - B_{22} \frac{{u^{0} }}{{r^{2} }} + D_{11} \left( {\frac{{\partial^{2} \alpha_{1} }}{{\partial r^{2} }} + \frac{{\partial \alpha_{1} }}{r \cdot \partial r}} \right) - D_{22} \frac{{\alpha_{1} }}{{r^{2} }} = K^{2} A_{44} \left( {\alpha_{1} + \frac{\partial w}{\partial r}} \right) $$

$$ K^{2} A_{44} \left( {\frac{{\partial \alpha_{1} }}{\partial r} + \frac{{\alpha_{1} }}{r} + \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial w}{r \cdot \partial r}} \right) = I_{0} \,\frac{{\partial^{2} w}}{{\partial \,t^{2} }}. $$

(12)

The following dimensionless parameters are introduced for convenience

$$ \begin{aligned} U &= \frac{{u^{0} \cdot (a - b)}}{{h^{2} }},\quad W = \frac{{w^{0} }}{h},\quad\alpha = \frac{{\alpha_{1} \cdot (a - b)}}{h}, \nonumber \\ \xi &= \frac{r - b}{a - b},\quad p = \frac{{q \cdot (a - b)^{4} }}{{E_{T} \cdot h^{4} }}, \hfill \nonumber \\ a_{44} &= \frac{{K^{2} \cdot A_{44} }}{{E_{T} \cdot h}},\quad b_{ij} = \frac{{B_{ij} }}{{E_{T} \cdot h^{2} }},\quad d_{ij} = \frac{{D_{ij} }}{{E_{T} \cdot h^{3} }}. \hfill \\ \end{aligned} $$

(13)

Here, E _T is the reference Young’s modulus. In case of laminated composites with layers of same material, E _T can be taken conveniently to be the Young’s modulus in the direction transverse to fiber direction.

Using the nondimensional quantities defined in (13), a set of equations of motion can now be written as

$$ \begin{aligned} &a_{11} \left( {\frac{1}{{(a - b)^{2} }} \cdot \frac{{\partial^{2} U}}{{\partial \xi^{2} }} + \frac{1}{(\xi \,a + (1 - \xi )b) * (a - b)} \cdot \frac{\partial U}{\partial \xi }} \right) - a_{22} \frac{U}{{(\xi \,a + (1 - \xi )b)^{2} }} \hfill \nonumber \\ &\quad + b_{11} \left( {\frac{1}{{(a - b)^{2} }} \cdot \frac{{\partial^{2} \alpha }}{{\partial \xi^{2} }} + \frac{1}{(\xi \,a + (1 - \xi )b) * (a - b)} \cdot \frac{\partial \alpha }{\partial \xi }} \right) - b_{22} \frac{\alpha }{{(\xi \,a + (1 - \xi )b)^{2} }} = \,0 \hfill \nonumber \\ &\quad b_{11} \left( {\frac{1}{{(a - b)^{2} }} \cdot \frac{{\partial^{2} U}}{{\partial \xi^{2} }} + \frac{1}{(\xi \,a + (1 - \xi )b) * (a - b)} \cdot \frac{\partial U}{\partial \xi }} \right) - b_{22} \frac{U}{{(\xi \,a + (1 - \xi )b)^{2} }} \hfill \nonumber \\ &\quad + d_{11} \left( {\frac{1}{{(a - b)^{2} }} \cdot \frac{{\partial^{2} \alpha }}{{\partial \xi^{2} }} + \frac{1}{(\xi \,a + (1 - \xi )b) * (a - b)} \cdot \frac{\partial \alpha }{\partial \xi }} \right) - d_{22} \frac{\alpha }{{(\xi \,a + (1 - \xi )b)^{2} }} = \frac{{a_{44} }}{{h^{2} }}\left( {\alpha + \frac{\partial W}{\partial \xi }} \right) \hfill \nonumber \\ &\quad a_{44} E_{T} h^{2} \left( {\frac{1}{(a - b)} \cdot \frac{\partial \alpha }{\partial \xi } + \frac{\alpha }{(\xi \,a + (1 - \xi )b)} + \frac{1}{(a - b)} \cdot \frac{{\partial^{2} W}}{{\partial \xi^{2} }} + \frac{1}{(\xi \,a + (1 - \xi )b)} \cdot \frac{\partial W}{\partial \xi }} \right) = \,I_{o} \,\frac{{\partial^{2} W}}{{\partial t^{2} }}. \hfill \\ \end{aligned} $$

(14)

Polynomial series solution by collocation at Chebyshev zeroes

To set up the eigenvalue problem for determination of free vibration frequencies and the corresponding mode shapes, in the present work, Chebyshev collocation method is used. The dependent variables U, α and W and their derivatives are expressed in Chebyshev series as

$$ \{ U(\xi ,t),\alpha (\xi ,t),W(\xi ,t)\} = \left\{ {\sum\nolimits_{n = 1}^{N + 1} {(U_{n} } ,\alpha_{n} ,W_{n} )\xi^{n - 1} } \right\}e^{i\omega t} . $$

(15)

Using Eq. (15) the equations of motion can now be written as

$$ \begin{aligned} & a_{11} \sum\limits_{n = 1}^{N + 1} {\left( {\frac{{(n - 1)(n - 2)U_{n} \xi^{n - 3} }}{{(a - b)^{2} }} + \frac{{(n - 1)U_{n} \xi^{n - 2} }}{(\xi \,a + (1 - \xi )b) * (a - b)}} \right)} - a_{22} \sum\limits_{n = 1}^{N + 1} {\frac{{U_{n} \xi^{n - 1} }}{{(\xi \,a + (1 - \xi )b)^{2} }}} \hfill \nonumber \\ &\quad + b_{11} \sum\limits_{n = 1}^{N + 1} {\left( {\frac{{(n - 1)(n - 2)\alpha_{n} \xi^{n - 3} }}{{(a - b)^{2} }} + \frac{{(n - 1)\alpha_{n} \xi^{n - 2} }}{(\xi \,a + (1 - \xi )b) * (a - b)}} \right)} - b_{22} \sum\limits_{n = 1}^{N + 1} {\frac{{\alpha_{n} \xi^{n - 1} }}{{(\xi \,a + (1 - \xi )b)^{2} }}} = 0 \hfill \nonumber \\ &\quad b_{11} \sum\limits_{n = 1}^{N + 1} {\left( {\frac{{(n - 1)(n - 2)U_{n} \xi^{n - 3} }}{{(a - b)^{2} }} + \frac{{(n - 1)U_{n} \xi^{n - 2} }}{(\xi \,a + (1 - \xi )b) * (a - b)}} \right)} - b_{22} \sum\limits_{n = 1}^{N + 1} {\frac{{U_{n} \xi^{n - 1} }}{{(\xi \,a + (1 - \xi )b)^{2} }}} \hfill \nonumber \\ &\quad + d_{11} \sum\limits_{n = 1}^{N + 1} {\left( {\frac{{(n - 1)(n - 2)\alpha_{n} \xi^{n - 3} }}{{(a - b)^{2} }} + \frac{{(n - 1)\alpha_{n} \xi^{n - 2} }}{(\xi \,a + (1 - \xi )b) * (a - b)}} \right)} - d_{22} \sum\limits_{n = 1}^{N + 1} {\frac{{\alpha_{n} \xi^{n - 1} }}{{(\xi \,a + (1 - \xi )b)^{2} }}} \hfill \\ \end{aligned} $$

(16)

$$ - \frac{{a_{44} }}{{h^{2} }}\sum\limits_{n = 1}^{N + 1} {\left( {\alpha_{n} \xi^{n - 1} + (n - 1)W_{n} \xi^{n - 2} } \right)} = 0 $$

(17)

$$ \frac{{a_{44} \cdot a^{4} }}{{(a - b)d11 \cdot h^{2} }}\sum\limits_{n = 1}^{N + 1} {\left( {\frac{{(n - 1)\,\alpha_{n} \,\xi^{n - 2} }}{(a - b)}\, + } \right.\frac{{\alpha_{n} \xi^{n - 1} }}{(\xi \,a\, + \,(1 - \xi )b)}\, + \,\frac{{(n - 1)(n - 2)\,W_{n} \xi^{n - 3} }}{(a - b)}} \left. { \, + \frac{{(n - 1)\,W_{n} \xi^{n - 2} }}{(\xi \,a + (1 - \xi )b)}} \right)\, = \, - \lambda \,^{2} \,\sum\limits_{n = 1}^{N + 1} {W_{n} \,\xi^{n - 1} } $$

(18)

$$ {\text{where }}\lambda \, = \, \omega \, a^{2} \sqrt {\rho h/D_{11} } . $$

(19)

Boundary conditions considered: The following combinations of boundary conditions have been considered in the present work.

Clamped boundary condition

$$ {\text{At outer boundary}}\;r = a,\quad u^{0} = \alpha_{ 1}^{0} = w^{0} = 0\quad {\text{ for both circular plate and annular plate}} . $$

$$ \begin{aligned} {\text{At inner boundary}}\;r = b,\quad \begin{array}{ll} u^{0} = \alpha_{ 1}^{0} = {\text{d}}w^{0} /{\text{d}}r = 0& {\text{ for circular plates and}} \hfill \\ u^{0} = \alpha_{ 1}^{0} = w^{0} = 0 & {\text{ for annular plates}}. \end{array} \hfill \\ \end{aligned} $$

Simply supported condition type

$$ {\text{At outer boundary}}\;r = a,\quad u^{0} = M_{r} = w^{0} = 0\quad {\text{ for both circular plate and annular plate}} . $$

$$ \begin{aligned} {\text{At inner boundary }} r = b,\quad\begin{array}{ll} u^{0} = \alpha_{ 1}^{0} = {\text{d}}w^{0} /{\text{d}}r = 0 & {\text{ for circular plates and}} \hfill \\ u^{0} = M_{r} = w^{0} = 0 & {\text{ for annular plates}} \end{array}\hfill \\ \end{aligned}. $$

Simply supported condition type

$$ {\text{At outer boundary}}r = a,\quad N_{r} = M_{r} = w^{0} = 0\quad{\text{ for both circular plate and annular plate}} . $$

$$ \begin{aligned} {\text{At inner boundary}}\;r = b,\quad\begin{array}{ll}u^{0} = \alpha_{ 1}^{0} = {\text{d}}w^{0} /{\text{d}}r = 0&{\text{ for circular plates and}} \hfill \\ N_{r} = M_{r} = w^{0} = 0&{\text{ for annular plates}}. \end{array}\hfill \\ \end{aligned} $$

The Nth-degree Chebyshev polynomial T ^* _N has N zeroes at

$$ \xi_{i} = \frac{1}{2}\left\{ {1 + \cos \left[ {\frac{(2 * i - 1)\pi }{2N}} \right]} \right\}\quad i \, = \, 1, \, 2,{ \ldots },N. $$

(20)

By forcing the satisfaction of each of the three differential equations at the (N − 1) zeroes of T ^*_(N−1) (ξ), 0 ≤ ξ ≤ 1—the (N − 1)th degree shifted Chebyshev Polynomial, along with the stipulation of the three boundary conditions at each edge the dynamic equilibrium equations, can be expressed by a set of algebraic equations as

$$ \left[ {L_{11} } \right]\left\{ U \right\} + \, \left[ {L_{12} } \right]\left\{ \alpha \right\} + \, \left[ {L_{13} } \right]\left\{ q \right\} + \, \left[ {L_{14} } \right]\left\{ W \right\} \, = \, \left\{ 0 \right\} $$

$$ \left[ {L_{21} } \right]\left\{ U \right\} + \, \left[ {L_{22} } \right]\left\{ \alpha \right\} + \, \left[ {L_{23} } \right]\left\{ q \right\} + \, \left[ {L_{24} } \right]\left\{ W \right\} \, = \, \left\{ 0 \right\} $$

$$ \left[ {L_{31} } \right]\left\{ U \right\} + \, \left[ {L_{32} } \right]\left\{ \alpha \right\} + \, \left[ {L_{33} } \right]\left\{ q \right\} + \, \left[ {L_{34} } \right]\left\{ W \right\} \, = \, - \lambda^{2} \left[ M \right]\left\{ W \right\} $$

(21)

where {U}, {α}, {q} and {W} are the vectors containing the unknown coefficients which are defined by following equations

$$ \left\{ U \right\}^{T} = \, \left\{ {U_{1} , \, U_{2} ,{ \ldots },U_{n + 1} } \right\}, $$

$$ \left\{ \alpha \right\}^{T} = \, \left\{ {\alpha_{1} , \, \alpha_{2} ,{ \ldots },\alpha_{n + 1} } \right\}, $$

$$ \left\{ q \right\}^{T} = \, \left\{ {W_{1} , \, W_{2} } \right\}, $$

$$ \left\{ W \right\}^{T} = \, \left\{ {W_{3} , \, W_{4} ,{ \ldots },W_{n + 1} } \right\}. $$

(22)

The Eq. (21) can be written together in matrix form as

$$ \left[ {\begin{array}{*{20}c} {[\bar{L}_{11} ]} & {[\bar{L}_{12} ]} \\ {[\bar{L}_{21} ]} & {[\bar{L}_{22} ]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\{ x\} } \\ {\{ y\} } \\ \end{array} } \right\}\, = \,\,\lambda^{2} \left[ {\begin{array}{*{20}c} 0 & 0 \\ {[\bar{M}_{21} ]} & {[\bar{M}_{22} ]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\{ x\} } \\ {\{ y\} } \\ \end{array} } \right\} $$

(23)

$$ {\text{where}}\quad \left\{ x \right\}^{T} = \left\{ {\left\{ U \right\}^{T} \left\{ \alpha \right\}^{T} \left\{ q \right\}^{T} } \right\}, \, \left\{ y \right\}^{T} = \left\{ W \right\}^{T} . $$

(24)

By matrix condensation, Eq. (23) can be rewritten as

$$ [\overline{K} ]\,\{ y\} \, = \,\lambda^{2} \,[\overline{M} ]\,\{ y\} . $$

(25)

The solution of the above eigenvalue problem leads to the determination of the natural frequencies and mode shapes of the laminated orthotropic circular and annular plates undergoing axisymmetric vibrations.

Results and discussion

A C-program developed by Antia (2002) is used in the present work for the free vibration analysis of laminated polar orthotropic circular and annular plates based on the solution methodology described in the preceding sections. Convergence and comparison studies were made to establish the validity of the method. Results of parametric studies are also presented. In all the results presented here, the orientations of the fibers in the layers are identified either as 0° or 90°, depending upon whether the layer is reinforced radially or circumferentially. The material properties along the principal directions are assumed to be the same in all the layers.

Free vibration frequencies of clamped isotropic circular plate are shown in Table 1. It can be seen from the results that converged results are obtained with 10–12 terms of the Chebyshev series approximation. Comparisons between the present results and those of the existing results based on the classical plate theory, three-dimensional plate theory and first-order shear deformation theory are made. Table 2 shows the fundamental natural frequencies of clamped isotropic circular plate which are in good agreement with the results obtained by Lin and Tseng (1998).

Table 1 Free vibration frequencies of isotropic circular plate for convergence study

Table 2 Fundamental natural frequencies of clamped isotropic circular plates

Good agreement between the present results and those of Lin and Tseng (1998) and Han and Liew (1999) for isotropic annular plates clamped at both edges is also seen in Table 3.

Table 3 Fundamental natural frequencies of clamped–clamped isotropic annular plate

Parametric study

Free vibration analysis has been carried out on orthotropic circular and annular plates. Material properties of specimens used in this study as obtained from literature (Lin and Tseng 1998) are as given below.

Material I: E _θ /E _r  = 5, G _rθ /E _r  = 0.35, G _rz /E _r  = 0.292, G _θz /E _r  = 0.292, υ _θr  = 0.3, ρ = 1.0.

Material II: E _θ /E _r  = 50, G _rθ /E _r  = 0.6613, G _rz /E _r  = 0.5511, G _θz /E _r  = 0.5511, υ _θr  = 0.26, ρ = 1.0.

Material III (ultra-high-modulus graphite epoxy): E _r  = 310 × 10³ N/mm², E _θ  = 6.2 × 10³ N/mm², G _rθ  = 4.1 × 10³ N/mm², υ _rθ  = 0.26, ρ = 1.613 × 10³ kg/m³.

In all the parametric studies reported herein, a 12-term solution is adopted hereafter, in computation of the free vibration response of different plates.

The results of parametric study to know the effect of the number of layers on the free vibration frequencies of a laminated annular plate with both the edges clamped are presented in Fig. 2. Figure 3 presents the results of a study conducted to study the effect of boundary conditions on free vibration frequencies of a laminated polar orthotropic annular plate. Effect of the size of the hole on the fundamental frequency of annular plates clamped at both edges is shown in Fig. 4.

Fig. 2

Effect of number of layers on fundamental natural frequencies of laminated polar orthotropic annular plates

Fig. 3

Effect of boundary conditions on fundamental natural frequencies of laminated polar orthotopic annular plates

Fig. 4

Effect of hole radius on fundamental natural frequencies of laminated polar orthotropic annular plates

Figure 5 shows the results of a study conducted to know the effect of orthotropy ratio on the free vibration frequencies of a two-layered asymmetric cross-ply annular plate with both the edges clamped.

Fig. 5

Effect of orthotropy ratio on fundamental natural frequencies of laminated polar orthotropic annular plates

A comparison of the natural frequencies calculated from the present shear deformation theory with those predicted by CPT is presented in Fig. 6. It can be observed that the effect of shear deformation is to decrease the free vibration frequencies in case of thick plates.

Fig. 6

Effect of shear deformation on fundamental natural frequencies of circular plates

Fundamental natural frequencies of polar orthotropic laminated circular plates with clamped and simply supported boundary conditions are listed in Table 4. Results show that natural frequencies are influenced by stacking sequence and the order of the magnitude of the fundamental frequency for the five different laminates. For annular plates, the effects of stacking sequence on natural frequencies when the inner and outer edges are either clamped or simply supported are illustrated in Table 5 and are similar to those for circular plates.

Table 4 Fundamental frequencies of polar orthotropic laminated circular plates composed of different materials; $\lambda = \omega a^{2} \sqrt {\rho h/D_{11} }$

Table 5 Fundamental frequencies of polar orthotropic laminated annular plates composed of different materials; $\lambda = \omega a^{2} \sqrt {\rho h/D_{11} }$

Results of the fundamental frequency of several polar orthotropic laminated circular plates with clamped or simply supported boundary conditions are shown in Table 6. The ultra-high-modulus graphite epoxy composites are used in the examples. They reveal that among these different stacking sequences, the smallest natural frequency occurs when the plate is composed of laminae in which fibers are oriented in circumferential direction only. It seems to be reasonable, since the displacement and curvature of the first vibration mode of the plates are varied in the radial direction only. Hence, the laminated plate having higher stiffness in the radial direction would produce higher natural frequency and vice versa. Because the fibers are placed along circumferential direction in this laminate, the stiffness in the radial direction is smaller than any other laminates.

Table 6 Fundamental natural frequencies of polar orthotropic laminated circular plates: effect of fiber orientation; material III; $\lambda = \omega a^{2} \sqrt {\rho h/D_{66} }$

Fundamental frequencies of C–C, S^a–C, C^a–S and S–S polar orthotropic laminated annular plates listed in Table 7 show that the order of the magnitude of the fundamental frequency for these five laminates is (0°) > (0°/90°//90°/0°) > (90°/0°/90°/0°) > (90°/0°/0°/90°) > (90°). The same behavior has been found for laminated plates given by Lin and Tseng (1998). Typical axisymmetric mode shapes (torsionless) corresponding to fundamental natural frequencies for the laminated circular and annular plates with different boundary conditions, showing the effect of stacking sequences, are plotted in Figs. 7, 8, 9, 10, 11 and 12.

Table 7 Fundamental natural frequencies of polar orthotropic laminated annular plates: effect of fiber orientation; material III; $\lambda = \omega a^{2} \sqrt {\rho h/D_{66} }$

Fig. 7

Fundamental mode shapes for laminated polar orthotropic clamped circular plates

Fig. 8

Fundamental mode shapes for laminated polar orthotropic simply supported circular plates

Fig. 9

Fundamental mode shapes for laminated polar orthotropic C–C annular plates

Fig. 10

Fundamental mode shapes for laminated polar orthotropic S^a–C annular plates

Fig. 11

Fundamental mode shapes for laminated polar orthotropic C^a–S annular Plates

Fig. 12

Fundamental mode shapes for laminated polar orthotropic S–S annular plates

Conclusions

Free vibration characteristics of composite circular and annular plates were studied in detail, with formulation based on a first-order shear deformation theory and a solution methodology employing the Chebyshev collocation technique. Convergence tests were conducted for the Chebyshev collocation technique and it can be seen that there is excellent convergence even when we take four or six terms in the series for the problem considered. Further, numerical results have aided to conclude that

• The solution method, based on collocating the equations of motion at Chebyshev zeroes as proposed herein, developed systematically in polar co-ordinates, is reliable and effective for finding natural frequencies and mode shapes of polar orthotropic circular and annular plates. The fundamental frequency of polar orthotropic laminated annular plates increases with an increase in number of layers, hole size and orthotropy ratio. Fundamental frequencies are higher for clamped boundary conditions.

• Transverse shear effects are more significant for polar orthotropic laminated plates than isotropic plates. Further, the transverse shear effects are negligible in case of thin plates.

• For polar orthotropic laminated circular and annular plates with clamped edges, the laminate stacked with all layers having fibers oriented along the radial direction has the highest fundamental frequency.

• Parametric studies conclude that free vibration frequencies are dependent not only on the radius to thickness ratio, but also on plate parameters such as the fiber orientation, lamination sequence, hole diameter and the boundary conditions.

Author contributions

A. Powmya carried out the study under the guidance of MCN. MCN also participated in the sequence alignment and drafted the manuscript. Both authors read and approved the final manuscript.