Buckling characteristic of multi-laminated composite elliptical cylindrical shells

Abstract

Fiber-reinforced composite materials continue to experience increased adoption in aerospace, marine, automobile, and civil structures due to their high specific strength, high stiffness, and light weight. This increased use has been accompanied by applications involving non-traditional configurations such as compression members with elliptical cross-sections. To model such shapes, we develop and report an improved generalized shell element called 4EAS-FS through a combination of enhanced assumed strain and the substitute shear strain fields. A flat shell element has been developed by combining a membrane element with drilling degree-of-freedom and a plate bending element. We use the element developed to determine specifically buckling loads and mode shapes of composite laminates with elliptical cross-section including transverse shear deformations. The combined influence of shell geometry and elliptical cross-sectional parameters, fiber angle, and lay-up on the buckling loads of an elliptical cylinder is examined. It is hoped that the critical buckling loads and mode shapes presented here will serve as a benchmark for future investigations.

Introduction

Because of their inherent light weight, high strength, and high durability, the proliferation of FRP (fiberglass reinforced plastic) composite materials, which are traditionally used in aerospace, shipbuilding, and automobile industries is gradually moving towards applications in newer areas such as the construction industry. Concurrent with this expanded use, emphasis on beauty and symbolism in such structures continues with non-traditional cross-sections such as elliptical sections becoming common. Subsequently, the use of these structures with non-traditional cross-sections as compression members gives rise to interesting buckling problems. Typically, buckling in compressive forces results in reduction in stiffness and load carrying capacity. There are two types of buckling, namely, global and local buckling of a member comprising the structural system. In both cases, it is important to make sure that local buckling does not precede global buckling; gas buckling of a component may cause re-distribution of stress leading to a consequential reduction in load carrying capacity of the entire member.

As a result, there is a need for a computational model to predict buckling for laminated composite compression members with non-traditional geometry such as an elliptical cross-section. Robust finite element particularly suited for buckling analysis of such structures could offer a substantially powerful analysis/design tool. In this paper, therefore, we develop an improved generalized shell element suitable for such configurations. Using the element, we will address the buckling characteristic of anisotropic laminated cylinders with elliptical cross-section considering the influence of various factors such as aspect ratio, lamination scheme, and slenderness ratio. It is believed that by presenting a study of linearized buckling mode shapes, a useful body of literature for understanding the stability of such structures will be made available for analysts and designers.

The variation of linearized buckling of isotropic cylindrical shells under axial loads with various parameters such as geometric shapes and initial defects were analyzed by a number of researchers including Koiter (1956), Sobel et al. (1976), and Chryssanthopulos et al. (1991). Kim et al. (2001) derived a design equation that solves the buckling stress simply through regression analysis. The research, which had been limited to isotropic material, was gradually expanded with growing interest in composite materials. Yoon (1999) and Park et al. (2000) performed the analysis of free vibration and buckling based on Mindlin Theory, which considers shear deformation effects. Park et al. (2000) analyzed the influences of initial geometric defects and the vibration amplitude in eigenvalue and nonlinear analyses of carbon fiber reinforced polymer (CFRP) circular panels. Based on those results, they further investigated sensitivity of geometric defects in CFRP circular panels and suggested the ‘knock-down’ factor used in the design of composite material panels. Recently, Chun et al. (2002) performed large deformation analysis of anisotropic cylindrical shells through derivation of governing equations considering geometric nonlinear terms. Yoon and Chae (1998) and Park et al. (2004) studied the buckling stability of laminated cantilever structures with channel cross-sections. They also investigated the effect of geometric shape factors on linearized buckling modes. Chang (2004) analyzed the buckling behaviors of multi-laminated cylindrical shells with transverse ribs for various parameters (the position and shape of the stiffener, the geometric shape of a shell, fiber angle, etc.). Based on their results, they suggested effective lamination design schemes applicable to stiffened laminated shells. With regard to shells of elliptical cross-section, the works of Sambandam et al. (2003) and Ganapathi et al. (2004) who reported on buckling and free vibration analysis are among the firsts. However, their results were limited to cross-ply and angle-ply laminations only. Further, their results did not address the global and local nature of the ensuing buckling mode shapes.

This current research, therefore, intends to fill in the gap that exists in modeling buckling behaviors of multi-laminated cylinders in composite material with elliptical cross-section and any general lay-up scheme. The versatile shell element developed in this study (called ‘4EAS-FS’) will be used to compare and analyze buckling load and modes for various parameters. The use of enhanced assumed strains and substitute shear strains help prevent shear and membrane locking phenomenon and spurious zero energy mode. The subspace iteration method, which analyzes eigenvalue problems with the Jacobi method, is applied in the subspace formed by substitution of the total space basic vector with the subspace basic vector.

Theory and formulations

Geometric shape and material data

Figure 1 shows an idealized model of laminated cylinders with elliptical cross-section that forms the focus of this paper. The lengths of each minor radius and major radius of the ellipse are given by ‘a’ and ‘b’. L defines the length in y-axis. The mid-plane of the component is set up as the xy-plane and the axis perpendicular to the mid-plane as the z-axis, and $\mathit{\theta }$ represents the fiber angle (see Fig. 2). The orthotropic material properties used in the analysis are $E_1/E_2=40$, $G_{12}=G_{13}=0.6E_2$, $G_{23}=0.5E_2$, and $\mathit{\nu }=0.25$. Layers with the same thickness and material are assumed to be laminated in the upward direction (+z direction) while the fiber angle is measured counterclockwise from the x-axis. A sketch of a typical model is shown in Fig. 3.

Fig. 1

Geometric shape of a laminated cylinder with elliptical cross-section

Fig. 2

Lamination components and coordinate system

Fig. 3

Finite element modeling formulation of finite elements

Formulation of Finite Elements

To improve the capability of laminated shell elements based on Mindlin-Reissner theory, we introduce (1) Donea and Lamain’s (1987) and Bathe and Dvorkin's (1986) assumed strain fields to the shear strain and (2) Hu-Washizu’s variational formulation of enhanced assumed strain to in-plane and bending strain (Simo and Rifai 1990; Andelfingr and Ramm 1993). In addition, a membrane element with drilling degrees of freedom is combined with a plate bending element to form a flat shell. We also use Allman’s (1988) shape functions for the displacement field corresponding to drilling degrees of freedom as well as the variational equation suggested by Hughes and Brezzi (1989). To eliminate membrane locking and secure accurate rank, and hence prevent a spurious zero energy mode, a 5-point integration scheme is adopted (Chun and Kassegne 2005).

The geometric stiffness matrix for buckling analysis for membrane loads, $N_x$, $N_y$ and $N_{xy}$, is presented in Eq. (1).

$$\begin{array}{cc}\hfill {\left[K_{\mathit{\sigma }}\right]}_{24\times 24}& ={\int }_V{[G]}_{24\times 2}\left[\begin{array}{cc}{N}_x& N_{xy}\\ N_{xy}& N_y\end{array}\right]{\left[G\right]}_{2\times 24}dV\hfill \\ \hfill & ={\int }_1^{-1}{\int }_1^{-1}{\left[G_I\right]}^T{\left[J\right]}^{-T}\left[\begin{array}{cc}{N}_x& N_{xy}\\ N_{xy}& N_y\end{array}\right]{\left[J\right]}^{-1}\left[G_I\right]\left|J\right|d\mathit{\xi }d\mathit{\eta }\hfill \\ \hfill \end{array}$$

(1)

$$[G]={[J]}^{-1}[G_I]$$

(2)

$$\left|[K_S]-\overline{\mathit{\lambda }}[K_{\mathit{\sigma }}]\right|=0.$$

(3)

Here, $[J]$ represents the Jacobian matrix, $|J|$ represents the Jacobian determinant, and $[G_I]$ stands for differential terms about $\mathit{\xi }$, $\mathit{\eta }$ of a shape function. Buckling analysis is expressed as an eigenvalue problem as in Eq. (3), $\overline{\mathit{\lambda }}$ stands for the linearized buckling load $N_{cr}$, and $K_S$ stands for the stiffness matrix.

Constitutive equation considering shear deformation

The strain-displacement and the stress-strain relationships in multi-laminated flat shells are not presented here since they are widely available in the literature (Reddy 2003). The constitutive equations of laminated shells are summarized as Eqs. (4) and (5).

$$\left\{\begin{array}{c}N\\ M\\ Q\end{array}\right\}=\left[\begin{array}{ccc}{A}_{ij}^1& A_{ij}^2& 0\\ A_{ij}^2& A_{ij}^3& 0\\ 0& 0& E_{ij}\end{array}\right]\left\{\begin{array}{c}\mathit{\epsilon }\\ \mathit{\kappa }\\ \mathit{\gamma }\end{array}\right\}$$

(4)

$A_{ij}^{\mathit{\alpha }}=\frac{1}{\mathit{\alpha }}\sum _{k=1}^{NL}{Q}_{ij}^{(k)}(h_{k-1}^{\mathit{\alpha }}-h_k^{\mathit{\alpha }})$,

$$E_{ij}=\frac{5}{4}\sum _{k=1}^{NL}{Q}_{ij}^{(k)}\left\{(h_{k-1}^{}-h_k^{})-\frac{4}{3h^2}(h_{k-1}^3-h_k^3)\right\}$$

(5)

where, $NL$ is number of lamina. $A_{ij}^1$ represents the extensional stiffness, $A_{ij}^3$ is the bending stiffness, $A_{ij}^2$ is the bending-extensional coupling stiffness, and $E_{ij}$ represents the shear stiffness. In order to ensure the continuity of the shear stress distribution in the thickness direction, the interpolation functions suggested by Vinson and Chou (1975) are applied instead of shear correction factor as in the second part of Eq. (5).

Fig. 4

Analysis model and critical buckling mode shape

Numerical result

Here, we specifically investigate buckling loads for various geometric shapes and fiber angles of laminated cylinders with elliptical cross-section. The geometric shape parameters of interest are elliptical aspect ratio ($a/b$) and slenderness ratio ($L/R$). In this case, $R(=c/2\mathit{\pi })$ is defined as the equivalent radius of the elliptical cross-section, and $c$ is the circumference of the ellipse as calculated from $c=\mathit{\pi }(a+b)\mathit{\beta }$, $\mathit{\beta }=1+3e^2/(10+{(4-3e^2)}^{1/2})$, and $e=(a-b)/(a+b)$ (Ramanujan 1913). The non-dimensionalized buckling loads reported here are expressed as $P=N_{cr}{R}^2/(E_2{t}^3)$. The basic model is a fixed-end supported laminated cylinder where $R=100\mathrm{mm}$ and $t=5\mathrm{mm}$ under an axial compressive load. First, we establish the validity of the element by comparing its performance with established results. Then, cross-ply laminated cylinders with circular and elliptical cross-sections are investigated followed by the same geometry with the angle-ply lamination scheme.

Validation of element (4EAS-FS)

The validity of the four-node enhanced assumed strain flat shell element developed here is first evaluated by comparing its performance with established results reported in the literature (Jaunky et al. 1999; Rikards et al. 2001) and general structural analysis software (STAGS, ANSYS, LUSAS). The convergence for various numbers of elements for each aspect ratio is also investigated. Figure 4 shows the details of the model considered and the critical buckling mode shape. A summary of the results is given in Table 1. It is shown that the results from the finite element, 4EAS-FS, developed here show very good agreement with those reported in the literature.

Table 1 Buckling load of cylindrical laminated shell (lbs/in)

Figure 5 demonstrates the convergence for buckling mode for various numbers of elements in laminated cylinders with elliptical cross-sections. The figure shows that convergence of >99 % is achieved for number of elements equal to or >40. Therefore, the number of elements used in the buckling analysis in this study is set to 40 in the circumferential direction and 20 in the axial direction.

Fig. 5

Convergence study for numbers of elements

Buckling behaviors of cross-ply laminated cylinders with circular and elliptical cross-sections

In this section, the variation of buckling behavior of laminated composite cylinders of elliptical cross-section (limited to cross-ply cases) with aspect ratio and the lamination scheme is investigated.

Symmetric cross-ply laminates show structurally more stable behaviors because the coupling stiffness, $B_{ij}$ is zero. In general, therefore, for a lamination scheme of realistic structures in composite materials, a symmetric laminate is preferred to minimize influence from coupling of stiffness terms. Figure 6 shows a summary of convergence study of symmetric laminate scheme with numbers of layers ($n$). It is observed that the buckling load converges for $n=5$ and above. Subsequently, this result helped establish the basic lamination scheme as ${(0/90)}_{5S}$.

Fig. 6

Convergence study for numbers of laminations

Figure 7 shows the comparison of critical buckling loads versus geometrical shape variations in the cases of symmetric cross-ply laminates. As shown in Fig. 7a, as the length L increases, the buckling load of the analysis model increases slowly followed by a steep decrease. A closer look at the corresponding mode shapes before and after ‘the point of inflection’ reveals a transition from two-dimensional buckling modes to three-dimensional buckling. In other words, above the point of inflection, buckling behavior identical to a column structure occurs more easily than buckling in a cross-section of the shell. Moreover, it can be seen that as the aspect ratio $a/b$ increases, total buckling occurs with relatively smaller slenderness ratio ($L/R$). This is largely because the curvature of the curved surface in the minor axis of the ellipse decreases and, therefore, the structural stiffness decreases correspondingly.

Fig. 7

Non-dimensional and standardized critical buckling load for various slenderness ratios

Table 2 compares a typical coupling stiffness term (B₁₁) in cross-ply laminate with numbers of layers and the corresponding critical buckling loads. The coupling stiffness, which is actually a function of material stiffness from lamination arrangement only decreases with the number of laminations. Further, as the influence of the coupling stiffness decreases, the buckling load is observed to increase by as much as 1.5 times (Yoon 1999; Chun et al. 2002). An overview of the results also indicates that change in buckling load for various numbers of layers becomes large when the $a/b$ ratio increases or slenderness ratio ($L/R$) decreases. In other words, the comparison of buckling loads with lamination numbers of 2 ($n=1$) and 16 ($n=8$) demonstrates differences of 1.44 times for $a/b=1.0$ and 1.58 times for $a/b=2.0$ (for $L/R=5.0$), and 1.4 times for $a/b=1.0$ and 1.53 times for $a/b=2.0$ (for $L/R=10.0$). In addition, when the number of layers is greater than 4 ($n=2$), the rate of decrease in the buckling load for various $a/b$ is about 40 %. Such phenomenon may be verified with a standardized buckling load distribution in Fig. 7b. For both anti-symmetric and symmetric laminates with number of layers equal to or greater than 16, the analysis results can be curve-fitted to the function, $y=-0.6Ln(x)+1.04$. Furthermore, the same curve-fitting method can be used to find the function for the thickness ratio ($R/t$) as illustrated in Fig. 7b.

Table 2 Non-dimensional critical buckling load for various numbers of laminations and aspect ratios

Table 3 gives a comprehensive comparison of critical buckling loads with elasticity coefficient ratio, $E_1/E_2$ and aspect ratio, a/b. The values in parenthesis in the table indicate normalization with respect to the buckling loads corresponding to a circular cross-section. The table shows that (1) decreasing curvature ($1/R_{\mathit{\alpha }}$) due to increase in the aspect ratio causes a corresponding decrease in the buckling stability (up to ~50 % for E ₁ /E ₂  = 10 and a/b = 2.00), and (2) stability in elliptical cross-section cylindrical shells seems to depend on material stiffness more strongly than in cylinders with a circular cross-section. Likewise, as the aspect ratio ($a/b$) is increased from 1.0 to 2.0 (from circular cross-section to elliptical cross-section), the buckling loads show a modest increase from 50 to 56 % with increased E ₁ /E ₂ ratios. The table also shows that increase in orthotropy (i.e., E ₁ /E ₂ ) has more severe consequences in lowering buckling loads for high aspect ratios (i.e., elliptical cross-sections) than lower ones (i.e., circular cross-section).

Table 3 Non-dimensional critical buckling load for various elasticity coefficient ratios and aspect ratios [$L/R=5.0$, ${(0/90)}_{5S}$]

Figure 8 compares different buckling modes of a circular cylinder ($a/b=1$) and an elliptical cylinder ($a/b=2$). The buckling mode shapes for laminated cylinders with elliptical cross-sections show repetitive 2-dimensional symmetric and anti-symmetric deformations about the main axis. In general, the buckling seems to occur accompanied with small curvatures on a 2-dimensional plane. This phenomenon is seen even for higher modes where the entire side face seems to participate. The fundamental and a higher buckling modes (9th-mode) for $L/R=5$ (which represents relatively long cylinders in axial direction) are presented in Fig. 9 for a/b = 1, 1.5, and 2.0. The figure suggests a development of side preferentiality of buckling mode both in circumferential- and axial-directions as the aspect ratio increases.

Fig. 8

Buckling modes of laminated cylinders with symmetric cross-ply ($L/R=2.5$) (a/b = 1.0, circular cross-section. a/b = 2.0, elliptical cross-section)

Fig. 9

Buckling modes of laminated cylinders ($L/R=5$, 1st & 9th-mode)

Buckling behaviors of angle-ply laminated cylinders with circular and elliptical cross-sections

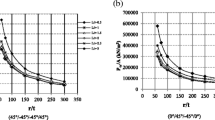
In this section, buckling loads are investigated for circular and elliptical cross-section cylinders with symmetric angle-ply ${(\mathit{\theta }/-\mathit{\theta })}_{5S}$ laminates for various aspect ratios ($a/b$). because of bending-extensional coupling of stiffness terms, anti-symmetric angle-ply laminates (for example, $(\mathit{\theta }/-\mathit{\theta })$ and ${(\mathit{\theta }/-\mathit{\theta })}_2$) have been reported to exhibit quite peculiar behavior accompanying decrease in buckling loads (Park et al. 2000 and Chun et al. 2002). The first set of results are summarized in Fig. 10 which illustrates that (1) the buckling loads for circular cross-section cylindrical shells are, in general, higher than those corresponding to elliptical cross-section shells for both single-layer and multi-laminates (converge to same values at 90° fiber angle for single-layers); (2) for single-layer cylinders, the effect of slenderness ratio tends to vanish at 90° fiber angle; (3) for symmetric laminates, the effect of slenderness ratio tends to vanish at a 45^o fiber angle for circular cylinders, and at about a 60° fiber angle for elliptical cross-section cylinders; and (4) for symmetric laminates, fiber reinforcement at the angle of $\pm 15$ about the axial direction seems to result in the greatest buckling load.

Fig. 10

Non-dimensional critical buckling load vs. aspect ratios and fiber angles

Table 4 contains a comprehensive summary of numerical results of non-dimensionalized buckling load versus various slenderness ratios ($L/R$) and aspect ratios ($a/b$). The following observations are made based on these summarized results. For fiber angle of $\pm 75$, the effect of slenderness ratio in decreasing the buckling load is minimum for all aspect ratios. For cases, when the fiber arrangement is in circumferential direction—that is, when the fiber angle is $\pm 15$, $\pm 30$ or $\pm 45$ —three-dimensional global buckling occurs and the buckling load decreases sharply for slenderness ratio roughly >5 or 10. For fiber angle ${(0/90)}_{5S}$, the buckling loads increase till a slenderness ratio of 20 for circular cylinders and 10 for elliptical cylinders. As shown in Fig. 11 as well, the buckling load corresponding to fiber angle of ${(75/-75)}_{5S}$ is greater than that of ${(0/90)}_{5S}$ fiber angle for slenderness ratios >22 or so for elliptical cylinders and 26 for circular cylinders. At lower slenderness ratios, a fiber angle of ${(0/90)}_{5S}$ gives higher buckling loads. In general, therefore, laminated cantilever cylinders with elliptical cross-section are structurally more stable with symmetric angle-ply of ${(75/-75)}_{5S}$ than with symmetric cross-ply of ${(0/90)}_{5S}$ after a certain length. By investigating the corresponding lengths versus aspect ratios, which result in greater buckling load with angle-ply laminates than cross-ply, curve-fitting gives a relation $y=5x^2-21x+42$. At a point above this function’s line, cylindrical shells with ${(75/-75)}_{5S}$ are more stable against axial compressive buckling than shells with ${(0/90)}_{5S}$ fiber angles.

Table 4 Non-dimensional critical buckling load versus various slenderness ratios and fiber angles

Fig. 11

Comparison of critical buckling loads of cross-ply and angle-ply

Figure 12 compares different modes of buckling deformations for various aspect ratios with a fiber angle of ${(75/-75)}_{5S}$, which showed the greatest buckling load documented in Table 4. The figure shows that the critical buckling mode of the fixed end supported shells tends to deform first at the free end. Our results indicate that similar deformations occur until the eighth mode. On the other hand, for the case of both ends fixed or simply supported, buckling is observed to occur predominantly along the axis of fiber reinforcements.

Fig. 12

Buckling modes of symmetric angle-ply laminates [${(75/-75)}_{5S}$, $L/R=5$]

Conclusion

In this research, the characteristics of buckling mode of laminated cantilever cylinder with elliptical cross-section subject to axial compressive force are presented. A program using the developed four-node EAS flat shell finite element is written. The assumed strain (substitute shear strain) and the enhanced strain are jointly applied to this finite element, and the capacity improved by the introduction of 5-point integration scheme to prevent the membrane locking and spurious zero energy mode.

Based on the numerical results obtained, the following conclusions are made:

• 1. Buckling analysis of a laminated cylinder with elliptical cross-section model for various parameters such as the aspect ratio, the slenderness ratio, and the fiber reinforcement angle shows that buckling occurs preferentially at a curved surface with a relatively small curvature in elliptical shells, and the buckling load decreases as the aspect ratio of cross-section increases.

• 2. Eigenvalue analysis of symmetric cross-ply laminates for various slenderness ratios demonstrates that the buckling load decreases linearly and then converges to a linear distribution.

• 3. Buckling modes corresponding to increasing slenderness ratio show a tendency towards three-dimensional buckling deformation (global buckling) at a slenderness ratio greater than a certain length. Subsequently, the corresponding slenderness ratio decreased as the aspect ratio increased.

• 4. Increase in orthotropy (i.e., E ₁ /E ₂ ) has more severe consequences in lowering buckling loads for elliptical cylindrical shells than circular cylindrical shells.

• 5. For symmetric angle-ply, the greatest buckling load occurred at the reinforcement angle of ±60–75°.

• 6. In addition, when the length was >25 times of the equivalent radius, it was observed that the buckling stability was more secured with symmetric angle-ply rather than with symmetric cross-ply.

• 7. By comparing and analyzing this phenomenon for various aspect ratios and slenderness ratios, an equation was suggested, which expresses the base line where buckling load becomes greater at angle-ply than cross-ply. In other words, in this research, the buckling load of laminated elliptical cylinders with symmetric cross-ply was expressed as ratios to that of laminated circular cylinders, which was suggested as numerical equations for each geometric parameter.

• 8. In addition, the slenderness ratio for each aspect ratio was calculated for the cases of having a greater buckling load with angle-ply ${(\mathit{\theta }/-\mathit{\theta }/\cdots )}_{nS}$ than symmetric-cross-ply ${(0/90/\cdots )}_{nS}$, and this was also expressed as numerical equations.

It is believed that this research can serve as important reference material for analyzing buckling modes of laminated cylinders with elliptical cross-section. Because the technique for reinforcing seismic performance by wrapping pier columns with composite material (FRP) was introduced recently, and because the increasing demand for beauty, symbolism, etc. in civil engineering drives the design and application of diversely shaped columns rather than circular columns, research about elliptical cylinder columns with exterior reinforcement with FRP (CFT with FRP) is necessary, and this paper is expected to be its basis. In further research, it is expected that the buckling analysis for more various boundary conditions and thickness ratios ($R/t$) will be performed and the effect of higher order shear deformation will be analyzed.