Introduction

Pulsed sieve-plate columns are essentially mass transfer devices in which two liquid phases come into contact and a solute is transferred from one liquid phase to the other liquid phase. The study of the mass transfer performance (efficiency) of a pulsed column is, therefore, essential for the design and operation of the column. Several studies [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] have already been performed on mass transfer characteristics of a pulsed sieve-plate tower and many correlations [4, 7, 9, 17, 18, 20, 23, 28] have been developed to predict the design and performance of a new column. However, due to the complex nature of the extraction process, the design procedures and practices (correlations) are not yet well established and usually pilot scale testing is required for such columns. Although some advanced modeling techniques [29,30,31,32,33,34] are currently acclaimed, however, for the reliable design strategies and computer methods to be well developed, more of such experimental studies (relationships among the column efficiency and operating parameters) on a pulsed sieve-plate column have to be accomplished for the various geometries and liquid–liquid systems. The review of the literature suggests that the dispersed phase holdup and mass transfer performance are generally studied for short columns with a few number of plates and with plate free area greater than 19%. In the present study, a unique, tall and relatively thin, column with 80 sieve plates and with a very low plate free area of 13.5% is selected to study its mass transfer characteristics. Acetic acid–kerosene–water system is chosen and the effect of operating parameters on the mass transfer performance of the column is studied. The present study will be useful in understanding the working of a tall, relatively thin, and low plate free area column and in the development of more general mass transfer correlations that are required in the design, scale up, and operation of a pulsed sieve-plate extraction column.

Experimental

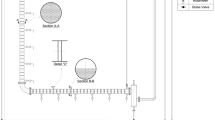
The experimental pulsed column consisted of 5.0 cm internal diameter glass shell with 80 number of sieve plates. Each sieve plate had 36 circular holes laid on triangular design and the plate free area was only 13.5%. The distance between the two plates was 5.0 cm and the total effective height (extraction section) of the column was 410 cm. The pulsations in the liquid body were produced by a piston type motor-driven pump. A schematic diagram of the column is given in Fig. 1 while additional detail of the experimental apparatus is given in Usman et al. [25]. Acetic acid–kerosene–water and propionic acid–kerosene–water systems were used to study the performance of the column. In each case, 5.0 wt% solution of an acid in kerosene was prepared and water was used as a solvent to extract the acid. The direction of mass transfer was, therefore, from organic phase which acted as the dispersed phase to the aqueous phase which was the continuous phase. Commercial kerosene was used. It was characterized in the laboratory by the specific gravity and the ASTM distillation tests. Acetic acid and propionic acid were of analytical grade and the water found in the laboratory was used as received without further purification. Table 1 gives the additional information about the chemicals used in the present study.

Fig. 1
figure 1

Experimental setup: a main extraction column with auxiliaries, b design of a single plate

Full size image
Table 1 Information regarding the chemicals used
Full size table

In a typical procedure, firstly, the whole of the column was filled with the aqueous phase (continuous phase) and being heavier, the aqueous phase was allowed to flow from the top to the bottom. Then, the kerosene phase (dispersed phase) pump was started and the dispersed phase was allowed to flow from the bottom to the top of the column in countercurrent mode to the flow of the aqueous phase. A sample was collected from the aqueous phase outlet after a regular interval and analyzed for the concentration of solute to observe the steady-state condition. The steady-state outlet concentration of the solute in aqueous phase was recorded and used in the calculations. The concentration of solute in outlet kerosene phase was calculated by considering kerosene and water phases as immiscible (dilute acid concentrations). The pulsation intensities and dispersed phase velocities were varied and a set of data was collected to be analyzed.

To observe the axial distribution of acetic acid, aqueous phase samples were taken at three different heights in the column and enough time was given in between any two withdrawals so that each sample was taken at steady state.

During an experimental run, the interface was maintained at the top in order to control flooding in the column. The interface was controlled manually by throttling the discharge valve of the aqueous phase flow [35] (at the bottom).

Results and discussion

Effect of operating parameters on mass transfer efficiency

For a pulsed sieve-plate column which is a type of differential contactor, the analysis of the mass transfer efficiency can be conveniently carried out using the concept of overall height of transfer unit or overall mass transfer coefficient. In the present study, the overall height of transfer unit and overall mass transfer coefficient are based on continuous phase and related to number of transfer units and height of the column as given in the following expression:

$$( {\text{HTU)}}_{\text{oc}} = \frac{{u_{\text{c}} }}{{K_{\text{oc}} a}} = \frac{H}{{({\text{NTU)}}_{\text{oc}} }},$$
(1)

where \(( {\text{NTU)}}_{\text{oc}}\), i.e., overall number of transfer units based on continuous phase is calculated using the experimental observations, i.e., using the inlet and exit molar concentrations of the phases involved. Assuming plug flow of the phases (negligible axial diffusivities in the phases) and considering both equilibrium and operating lines to be straight (dilute solutions), overall number of transfer units may be defined as apparent number of transfer units as given by the following expression [9, 25]:

$$( {\text{NTU)}}_{\text{ocp}} = \frac{1}{{\left( {\frac{{(y_{\text{i}} - y_{\text{o}} )}}{{m \cdot (x_{\text{o}} - x_{\text{i}} )}}} \right) - 1}}\ln \left( {\frac{{y_{\text{i}} - m \cdot x_{o} }}{{y_{\text{o}} - m \cdot x_{i} }}} \right),$$
(2)

where m is the equilibrium constant in the expression \(y = m \cdot x\). The value of m was calculated experimentally by taking various concentrations of solute in virtually equal amounts of kerosene and water. The experimental value of m was obtained as 0.0708 for the acetic acid–water–kerosene system and 0.2801 for the propionic acid–water–kerosene system.

The overall apparent mass transfer coefficient based on continuous phase was calculated using the following equation [25, 36]:

$$K_{\text{ocp}} a = \frac{{ ( {\text{NTU)}}_{\text{ocp}} \cdot u_{\text{c}} }}{H}.$$
(3)

Effect of pulsation intensity

Figure 2a, b shows the effect of pulsation intensity (the product of pulsation frequency and pulsation amplitude) on the height of transfer unit (HTUocp) and mass transfer coefficient (K ocp a), respectively, for acetic acid–water–kerosene system. As mentioned before, the acetic acid was taken as a solute in the kerosene phase and the direction of mass transfer was from kerosene (dispersed) phase to aqueous (continuous) phase. No phase inversion was observed during the operation. It is observed that increasing pulsation intensity continuously decreases the height of transfer unit and consequently increases the mass transfer coefficient for constant values of superficial velocities of the continuous and dispersed phases. It can be seen from Fig. 2 that the rate of decrease of HTUocp is initially higher and steadily decreases with an increase in pulsation intensity and may reach a steady minimum value. It is observed that in the first half of the range of Af studied, the height of transfer unit decreases from 4.14 to 3.57 m (13.7% decrease) and in the lower half it decreases from 3.57 to 3.30 m (7.61% decrease). This suggests that with an increase in pulsation intensity, initially height of transfer unit decreases more rapidly and then decreases at a relatively lower rate. Cohen and Beyer [1] for boric acid–water–isoamyl alcohol system, Smoot and Babb [9] for both acetone–water-1,1,2-trichloroethane system and acetic acid–water–methyl isobutyl ketone (MIBK) system, Gourdon and Casamatta [15] for acetone–water–toluene system, Venkatanarasaiah and Varma [17] for both n-butyric acid–kerosene–water system and benzoic acid–water–kerosene system, Li et al. [22] for nitric acid–30% TBP (in kerosene)–water system, He et al. [23] for caprolactam–water–benzene system, Jahya et al. [24] for acetone–water–toluene system, Usman et al. [25] for acetic acid–water–ethyl acetate system, and Torab-Mostaedi et al. [27] for both acetone–water–toluene system and acetone–water–butylacetate system have observed a continuous and generally a similar increase in mass transfer performance with an increase in pulsation intensity.

Fig. 2
figure 2

Effect of pulsation intensity on mass transfer performance: a height of transfer unit, b mass transfer coefficient. Solid lines are just to show the trends

Full size image

The height of transfer unit and, therefore, mass transfer performance may depend on drop size and dispersed phase holdup. Increase in pulsation intensity increases the energy supply to the column and, therefore, decreases the diameter of the dispersed phase drops which in effect increases the mass transfer surface area and, therefore, mass transfer efficiency [37, 38]. The increase in dispersed phase holdup may increase the residence time [37] and, therefore, may aid in increasing the mass transfer performance. However, a higher value of the dispersed phase holdup such as in the mixer-settler regime not necessarily means a decrease in height of transfer unit and, therefore, increase in dispersed phase holdup not always an indication of an increase in mass transfer efficiency. Figure 2 suggests that height of transfer unit continuously decreases and corresponding mass transfer coefficient continuously increases with an increase in pulsation intensity. In our previous work [39] on the dispersed phase holdup in the same column as studied in the present contribution and for the system kerosene–water (no solute addition) under virtually the same operating conditions, the mixer-settler regime was observed in the range of Af equal to 3.01 × 10−3 to ~17.0 × 10−3 m/s. Comparing these findings to Fig. 2, for the mixer-settler regime, therefore, one may say that though dispersed phase holdup decreases with an increase in Af but mass transfer efficiency, i.e., K ocpa increases (HTUocp decreases) with an increase in Af. It is, therefore, concluded that as the diameter of the dispersed phase drop decreases more rapidly than the holdup and contributes more towards mass transfer, the overall effect is the increase in mass transfer efficiency [17]. In support of that, it is important to mention here that unlike dispersed phase holdup, the average drop size of the dispersed phase always decreases with an increase in pulsation intensity [26, 40,41,42,43,44]. Further, it may be deduced from Fig. 2 that the effect of pulsation intensity on mass transfer efficiency is more pronounced in the mixer-settler region compared to the effect for the region beyond the mixer-settler region (dispersion region).

Effect of dispersed phase velocity

Figure 3 shows the effect of dispersed phase velocity on the height of transfer unit for acetic acid–water–kerosene system under various values of pulsation intensities. Again, the acetic acid was taken as a solute in the kerosene phase and the direction of mass transfer was from kerosene (dispersed) phase to aqueous (continuous) phase. In each case, clearly, the dispersed phase (kerosene) velocity has a profound effect on the mass transfer performance of the column. Increasing the dispersed phase velocity markedly decreases the height of transfer unit. Again, it is observed that the rate of decrease of height of transfer unit also decreases with increase in dispersed phase velocity. It can be seen from Fig. 3 that increasing four times the dispersed phase velocity decreases virtually four times the height of transfer unit. In the literature, Smoot and Babb [9] for both acetone–water-1,1,2-trichloroethane system and acetic acid–water–methyl isobutyl ketone (MIBK) system, Gourdon and Casamatta [15] for acetone–water–toluene system (u c + u d), Venkatanarasaiah and Varma [17] for both n-butyric acid–kerosene–water system and benzoic acid–water–kerosene system, He et al. [23] for caprolactam–water–benzene system, Jahya et al. [24] for acetone–water–toluene system, Usman et al. [25] for acetic acid–water–ethyl acetate system, and Torab-Mostaedi et al. [27] for both acetone–water–toluene system and acetone–water–butylacetate system have observed a continuous increase in mass transfer performance with increase in dispersed phase velocity. Similar to a change in pulsation intensity, a change in dispersed phase velocity also affects both the dispersed phase drop diameter and the dispersed phase holdup. However, unlike increase in pulsation intensity an increase in dispersed phase velocity continuously decreases the dispersed phase holdup.

Fig. 3
figure 3

Effect of dispersed phase velocity on height of transfer unit Solid lines are just to show the trends

Full size image

Variation of acetic acid concentration in the axial direction

Figure 4a, b shows the variation of acetic acid concentration in aqueous phase along the height of column at two different pulsation intensities as a function of dispersed phase velocities. Axial concentration was measured at three points in the column in addition to the exit and inlet points. As expected, the concentration of acetic acid increases continuously in the aqueous phase along the axial position from the inlet of the solvent (water) at the top to the exit at the bottom. It is observed that an increase in pulsation intensity does not affect the shape of the concentration profile; however, the average slope becomes less steep with a decrease in dispersed phase velocity.

Fig. 4
figure 4

Effect of axial position on the molar concentration of acetic acid in aqueous phase: a Af = 19.33 × 10−3 m/s, b Af = 26.0 × 10−3 m/s. Solid lines are just to show the trends

Full size image

Effect of solute type

One experimental run was also performed with 5.0 wt% propionic acid as a solute in kerosene and extraction was carried out using water as the solvent. The results were compared with 5.0 wt% acetic acid in kerosene with water as the solvent. Table 2 shows that a higher value of mass transfer coefficient was obtained with propionic acid as the solute compared to when acetic acid was the solute. This may be due to decreased diameter of the dispersed phase and increased dispersed phase holdup with propionic acid in the solution. Owing to the greater affinity of propionic acid with kerosene than acetic acid with kerosene, a decreased value of interfacial tension is expected for the propionic acid–water–kerosene system than acetic acid–water–kerosene system. This may suggest a decreased drop size and, therefore, a greater interfacial area which gives rise to increased value of the mass transfer coefficient. Table 3 shows a comparison of the present study with two other kerosene-carboxylic acid–water systems studied by Venkatanarasaiah and Varma [17] carboxylic acids with slight different conditions and column geometry.

Table 2 Effect of solute on the HTUocp and K ocp a
Full size table
Table 3 Comparison of mass transfer efficiencies for different pulsed column systems
Full size table

Correlation development for mass transfer coefficient

Yadav and Patwardhan [45] have reviewed the published correlations for mass transfer coefficient. Using a large number of experimental data (from literature), they tested the validity of the available correlations for predicting mass transfer coefficients. They have concluded that none of the available mass transfer correlations can satisfactorily represent the experimental data and, therefore, the design of a pulsed sieve-plate column should be based on pilot scale testing of the new system. However, for the experimental data generated in the present study, the correlation of Venkatanarasaiah and Varma [17] was tested. The equation was chosen because of its simplicity having a few variables and with a few parameters to be fitted. Moreover, as both for the dispersed phase holdup and slip velocity, the equations of Venkatanarasaiah and Varma [17] were found in relatively better agreement to the experimental data obtained on the same column in our previous study [39]. It is important to mention here that the equation of Venkatanarasaiah and Varma [17] has been developed for overall apparent mass transfer coefficient, i.e., it is based only on the measurable values of the inlet and exit concentrations and the equilibrium relationship for the system and without considering any axial mixing in the system. The mass transfer coefficients obtained in Sect. 3.1 are also apparent values and not corrected for the axial mixing. Based on the results obtained, a new mass transfer correlation is also developed.

All the experimental data were arranged in Microsoft Excel spreadsheet and subjected to regression in Solver® program. The following objective function was minimized:

$${\text{SSE}} = \sum\limits_{i = 1}^{i = N} {((K_{\text{ocp}} a)_{\text{obs}} - (K_{\text{ocp}} a)_{\bmod } )^{2} },$$
(4)

where SSE stands for the sum of squares of the errors, \((K_{\text{ocp}} a)_{\text{obs}}\) is the observed or experimental value of the mass transfer coefficient, \((K_{\text{ocp}} a)_{\bmod }\) is the model value of the mass transfer coefficient, i represents the ith value, and N is the total number of data points.

Testing of Venkatanarasaiah and Varma’s equation [17]

The following correlation is developed by Venkatanarasaiah and Varma [17] for the prediction of overall apparent mass transfer coefficient based on the continuous phase:

$$\it K_{\text{ocp}} a = K \cdot ({\text{Af}})^{0.84} \cdot d_{\text{o}}^{ - 0.21} \cdot \alpha^{ - 0.44} \cdot p^{ - 0.41} \cdot u_{\text{d}}^{0.91}.$$
(5)

The authors suggested that the constant K is dependent on the solute-liquid–liquid system used. Therefore, the equation was fitted against the experimental data and K was taken as the only parameter to be fitted. The value of K was found to be 0.0170. Figure 5 shows the validity of Venkatanarasaiah and Varma’s equation [17] for the experimental data of the present study, whereas Table 4 shows the values of the statistical parameters to show the goodness of the fit. Clearly, the equation is found not appropriate to fit the experimental data and quite a low value of R2 is obtained.

Fig. 5
figure 5

Scatter diagram between measured mass transfer coefficient and that calculated from the equation of Venkatnarasaiah and Varma [17], Eq. 5

Full size image
Table 4 Comparative fitting behavior of the correlations of mass transfer coefficient
Full size table

Development of the correlation for the mass transfer coefficient

In the first attempt, only three parameters were taken in consideration to develop the correlation suitable to the system studied in the present work and the following equation was used to fit the experimental data:

$$\it K_{\text{ocp}}\, a = K \cdot ({\text{Af}})^{a} \cdot u_{\text{d}}^{\text{b}} \cdot u_{\text{c}}^{\text{c}}.$$
(6)

The equation was fitted with the experimental data and in contrast to the use of the equation of Venkatanarasaiah and Varma [17] a much better fit was obtained. The SSE was reduced from 2.38 to 0.446 and the corresponding R 2 was improved from 0.504 to 0.795. However, a low value of the exponent of u c suggested to remove the variable u c and to modify the equation. In the next attempt, the variable u c was eliminated from the equation and the modified equation was subjected against the experimental data. Virtually the same values of SSE and R 2 were obtained and, therefore, suggested the equation to be retained as the final best-fit equation. The final equation with its parameters that described the experimental data was obtained as:

$$\it K_{\text{ocp}}\, a = 0.1145 \cdot ({\text{Af}})^{0.2578} \cdot u_{\text{d}}^{1.062}$$
(7)

SSE and R 2 values of Eq. 7 are given in Table 4 and Fig. 6 shows the scatter diagram between the measured K ocp a and the K ocp a values calculated from Eq. 7. The average percentage error as obtained from Eq. 8 was only 10.76%.

$$\% {\text{Error}} = \left( {\frac{{\left| {(K_{\text{ocp}} a)_{\text{obs}} - (K_{\text{ocp}} a)_{\bmod } } \right|}}{{(K_{\text{ocp}} a)_{\text{obs}} }}} \right) \times 100.$$
(8)
Fig. 6
figure 6

Scatter diagram between measured mass transfer coefficient and that calculated from Eq. 7

Full size image

Mathematical modeling of the pulsed column

A differential element of thickness Δz was selected in the body of the pulsed sieve-plate column, as shown in Fig. 7, and a mass balance was applied across the differential element.

Fig. 7
figure 7

The control element for mathematical modeling of the pulsed sieve-plate extraction column

Full size image

The following equations (for the dispersed phase and the continuous phase) were obtained in terms of overall mass transfer coefficient based on the continuous phase:

For continuous phase:

$$E_{\text{x}} \frac{{{\text{d}}^{2} x}}{{{\text{d}}z^{2} }} + u_{\text{c}} \frac{{{\text{d}}x}}{{{\text{d}}z}} + K_{\text{oc}} a(x_{\text{e}} - x) = 0.$$
(9)

For dispersed phase:

$$E_{\text{y}} \frac{{{\text{d}}^{2} y}}{{{\text{d}}z^{2} }} - u_{\text{d}} \frac{{{\text{d}}y}}{{{\text{d}}z}} - K_{\text{oc}} a(x_{\text{e}} - x) = 0.$$
(10)

As the system studied did not involve any heat effects, therefore, energy balance was not required in modeling the column.

Mass transfer in the absence of axial diffusivities

As for a tall column with a small diameter such as that studied here, mass transfer process due to axial diffusivities was expected to be negligible in comparison to the mass transfer by convection (bulk liquid flows); therefore, the first term of both Eqs. 9 and 10 was neglected and the following equations were obtained as desired.

For continuous phase:

$$u_{\text{c}} \frac{{{\text{d}}x}}{{{\text{d}}z}} + K_{\text{oc}} a(x_{\text{e}} - x) = 0.$$
(11)

For dispersed phase:

$$u_{\text{d}} \frac{{{\text{d}}y}}{{{\text{d}}z}} + K_{\text{oc}} a(x_{\text{e}} - x) = 0.$$
(12)

Rearranging Eqs. 11 and 12 and writing K oc a as K ocp a, i.e., in terms of overall apparent mass transfer coefficient, it may be shown that

For continuous phase:

$$\frac{{{\text{d}}x}}{{{\text{d}}z}} = \frac{{K_{\text{ocp}} a(x - x_{e} )}}{{u_{c} }}.$$
(13)

For dispersed phase:

$$\frac{{{\text{d}}y}}{{{\text{d}}z}} = \frac{{K_{\text{ocp}} a(x - x_{\text{e}} )}}{{u_{\text{d}} }}.$$
(14)

Equations 13 and 14 are the first-order ordinary differential equations and can be simultaneously solved using the appropriate boundary conditions as given in Eqs. 15 and 16 to obtain the concentration profiles for both the continuous and dispersed phases.

$${\text{At}}\;\;z = \, 0,y = y_{\text{i}} \,{\text{and}}\;x = x_{\text{o}}$$
(15)
$${\text{At}}\;\;z = H,y = y_{\text{o}} \;{\text{and}}\;x = x_{\text{i}}.$$
(16)

The solution requires the values of u c , u d , K ocp a, and an equilibrium relationship between molar concentration of solute in each of the continuous and dispersed phases.

In Sect. 3.4.2, the experimental data obtained in the present study were used to obtain a relationship (Eq. 7) of mass transfer coefficient in terms of pulsation intensity and dispersed phase velocity which was used to obtain the value of K ocp a in solving Eqs. 13 and 14. The values of u c and u d were obtained from the experimental data. The expression \(y = 0.0708x\) was used for the equilibrium value, where 0.0708 is the equilibrium constant for acetic acid–kerosene–water system.

The differential equations along with the auxiliary equations and boundary conditions were solved in POLYMATH (an established mathematical software) using RKF-45 (Runge–Kutta-Fehlberg-45) routine and concentration values of acetic acid in both the continuous (water) and dispersed (kerosene) phases were obtained at five different points in the column. It is important to mention here that the given problem was a countercurrent problem, so the initial values of outlet concentration of acetic acid in aqueous phase were found by trial and error. Initially, the experimental value of the outlet concentration of acetic acid in aqueous solution was used as a guess value and then the inlet concentration of acetic acid in water was compared with the experimental value (which was zero). If the predicted inlet aqueous phase concentration was different than zero, then a new initial value was used. The procedure was carried on till the predicted and actual values were numerically equal.

Figures 8 and 9 show the concentration profiles for various pulsation intensities and dispersed phase velocities, respectively. Increasing pulsation intensities, the slope of the concentration profile somehow decreases and shows a greater change in concentration of the acetic acid. This is also the case with the effect of dispersed phase velocity as shown in Fig. 9.

Fig. 8
figure 8

Model concentration profiles at various indicated pulsation intensities. u c  = 3.803 × 10−3 m/s, u d  = 3.642 × 10−3 m/s

Full size image
Fig. 9
figure 9

Model concentration profiles at various indicated dispersed phase velocities. u c  = 3.803 × 10−3 m/s, Af = 19.333 × 10−3 m/s

Full size image

In Fig. 9, for u d = 7.173 × 10−3 m/s, the two profiles actually crosses between 0.5 and 0.6 fractional height (axial position in the column to the total height of the column). This concentration cross in profiles does not mean the mass was not transferred at or after this point or the direction of mass transfer was reversed after this point. Concentration difference in two different liquid phases is not like temperature difference for heat transfer where no temperature difference means no transfer of heat. It is the effective concentration difference which is important and which may be calculated by the equilibrium relationship. The effective concentration difference is, therefore, not y – x, but y – y e, where y e is mx e . Now as m is quite a small fractional value (m = 0.0708) the effective concentration difference is positive throughout the column length.

Figure 10 shows the concentration profiles at a constant pulsation intensity of Af = 19.333 × 10−3 m/s and for varying dispersed phase velocities and compares the model concentration profiles to the experimental concentration profiles obtained in the present study. Though not perfect, but the model profiles give virtually the same trend and show rather good representation of the axial concentrations.

Fig. 10
figure 10

Comparison of concentration profiles at various indicated dispersed phase velocities. u c  = 3.803 × 10−3 m/s, Af = 19.333 × 10−3 m/s

Full size image

Mass transfer in the presence of axial diffusivities

The model equations, Eqs. 9 and 10, involve axial diffusivities. The equations were rearranged to obtain the following expressions:

For continuous phase:

$$\frac{{{\text{d}}^{2} x}}{{{\text{d}}z^{2} }} + \frac{{u_{\text{c}} }}{{E_{\text{x}} }}\frac{{{\text{d}}x}}{{{\text{d}}z}} + \frac{{K_{\text{oc}} a(x_{\text{e}} - x)}}{{E_{\text{x}} }} = 0.$$
(17)

For dispersed phase:

$$\frac{{{\text{d}}^{2} y}}{{{\text{d}}z^{2} }} - \frac{{u_{\text{d}} }}{{E_{\text{y}} }}\frac{{{\text{d}}y}}{{{\text{d}}z}} - \frac{{K_{\text{oc}} a(x_{\text{e}} - x)}}{{E_{\text{y}} }} = 0.$$
(18)

Unlike Eqs. 13, 14, 17, and 18 are second-order ordinary differential equations and can be solved by writing each second-order differential equation into two first-order ordinary differential equations. This way four ordinary differential equations were solved simultaneously using the appropriate boundary conditions as given in Eq. 19 through Eq. 22. For Eqs. 21 and 22, y is taken as y i and x is taken as x i , respectively.

$${\text{At}}\;\;z = \, 0, \quad \frac{{{\text{d}}x}}{{{\text{d}}z}} = 0$$
(19)
$${\text{At}}\;\;z = H, \quad \frac{{{\text{d}}y}}{{{\text{d}}z}} = 0$$
(20)
$${\text{At}}\;\;z = \, 0, \quad \frac{{{\text{d}}y}}{{{\text{d}}z}} = \frac{{u_{\text{d}} }}{{E_{\text{y}} }}(y - y_{\text{i}} )$$
(21)
$${\text{At}}\;z = H,\quad \frac{{{\text{d}}x}}{{{\text{d}}z}} = \frac{{u_{\text{c}} }}{{E_{\text{x}} }}(x_{\text{i}} - x)$$
(22)

Equations 17 and 18 together with boundary conditions were solved to fit the experimental axial concentrations. The fitting was obtained so that the SSE between the experimental and predicted axial concentrations was minimized. In each case, the %error between the experimental and model outlet concentrations in the dispersed phase was kept less than 5% and the inlet concentration of acetic acid in water was required to have a value of virtually equal to zero.

Table 5 shows the values of the axial diffusivities and mass transfer coefficients obtained by solving Eqs. 17 and 18. These mass transfer coefficients are not the overall apparent mass transfer coefficients but that are based on including the effect of axial dispersions and here called simply as overall mass transfer coefficients. The table also shows a comparison between the overall apparent mass transfer coefficients (obtained without using axial diffusivities in the column) and overall mass transfer coefficients (based on axial diffusivities) and describes that the two types of mass transfer coefficients are virtually the same. Figure 11 shows a typical comparison between an experimental concentration profile and the concentration profiles based on the model results with and without the use of axial diffusivities. The results show that virtually the same outcomes are obtained with and without using axial dispersions in the model and may suggest insignificance of model axial diffusivities in the column. The higher value of the outlet molar concentration without using axial diffusions in the model may be due to the reason that the correlation (Eq. 7) used to find K ocp a has already ~11% error as discussed earlier.

Table 5 Diffusivities and mass transfer coefficients obtained with and without the use of axial diffusivities
Full size table
Fig. 11
figure 11

Comparison of experimental axial concentration profile with model axial concentrations obtained with and without the use of axial diffusivities. u c  = 3.803 × 10−3 m/s, u d  = 4.524 × 10−3 m/s, Af = 19.333 × 10−3 m/s

Full size image

Conclusions

The mass transfer performance in a liquid phase pulsed sieve tray column of 50 mm diameter and 4 m height, with 80 trays with a plate free area of 13.5% was investigated. The mass transfer performance appears to be a strong function of both the pulsation intensity and dispersed phase velocity. The number of transfer units (NTUocp), the height of transfer unit (HTUocp), and the apparent mass transfer coefficient based on continuous phase (K ocp a) is calculated. Mass transfer coefficient increases with an increase in pulsation intensity and dispersed phase velocity. Variation of the concentration of acetic acid in aqueous phase along the length of the column is discussed as a function of dispersed phase velocity and pulsation intensity. Mass transfer coefficient of propionic acid as the solute in the kerosene phase is observed to be greater than when acetic acid is the solute in the kerosene phase.

For the experimental data of mass transfer coefficient, the equation of Venkatnarasaiah and Varma [17] for mass transfer coefficient is tried which, however, is found not successful. Venkatnarasaiah and Varma [17] worked on a column with plate free area ranging between 23 and 46%. This may be the reason that the data in the present study are not fitted well by their equation.

A new correlation that is, at least, applicable for the liquid–liquid system and the column studied in the present work is developed. The new equation gives a %error of only 10.8 as calculated from Eq. 8.

Mathematical modeling of the pulsed column is carried out with and without using the axial diffusivities. Based on the model without incorporating axial diffusivities, the concentration profiles for acetic acid in continuous (aqueous) phase and dispersed phase for various operating conditions are shown and in some cases compared with the experimental data. Based on the model considering axial diffusivities, model axial diffusivities and mass transfer coefficients are calculated. Virtually, similar mass transfer coefficients with and without the use of axial diffusivities in a model are obtained and virtually the similar concentration profiles are obtained that may show the insignificance of axial diffusivities in the column. The results may support the assumption of negligible axial diffusivities in the model as applied in the determination of mass transfer coefficients and in developing the corresponding mass transfer correlation (Eq. 7).