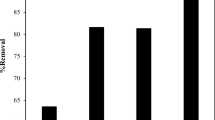Introduction

Many dyestuffs were used in textile dyeing and printing processes, which are non-biodegradable. Among the dyes, anionic dyes are carcinogenic and have the highest risk of diseases due to its toxic in nature. The presence of ethylene glycol in AB-FFS dye is responsible for producing a variety of illnesses such as proteinuria, uremia and anuria which are toxic to the liver and kidney [1, 2]. In recent days, treating the anionic dyes becomes a big challenge and several methods failed to produce satisfactory results.

Based on previous reports, adsorption methods do offer the most efficient technique used for the removal of dyes and pigments from industrial effluents. Adsorbents such as activated carbon [3], pith carbon [4], bagasse fly ash [5], rice husk [6] and cashew nut shell [7] have been used for dye decolorization under the batch mode. All these adsorbents had limited success over the industrial effluent treatments. Moreover, equilibrium data from batch mode provides fundamental information, but not applicable for real-time process. Therefore, there is a need to investigate the fixed bed column study to obtain engineering data for scaling up from laboratory-scale to pilot-scale level. Recently, a variety of natural adsorbents such as pistachio hull waste [8], dried Moringa oleifera seeds [9], orange peel cellulose [10] and Artocarpus heterophyllus [11] have been reported for the removal of heavy metals and dyes.

Earlier studies have confirmed that Moringa oleifera seed as biosorbent, which has polypeptides of molecular weight ranging from 6 to 16 kDa and its isoelectric pH value 10, contains high zeta potential, and cationic and anionic properties. Considering these properties, Moringa oleifera could be used as a good biosorbent when it is encapsulated. Our previous studies have reported that encapsulated Moringa oleifera beads are effectively used for the removal of heavy metals [9]. Hence, this present study is focused on the performance of encapsulated Moringa oleifera seed powder by cross-linking with polymer Ca-alginate, to obtain stable beads and used for its biosorption efficiency for AB-FFS solution. The biosorbent was investigated in batch as well as fixed bed column packed with MEA with respect to flow rate and bed height. Eventually, the isotherm, kinetics and breakthrough curve analysis for the removal of AB-FFS dyes were investigated.

Materials and methods

Preparation of dye solutions

The Anionic Blue-FFS dye was manufactured by Dynamic Industries Ltd, India. It is an anionic dye which is referred to as Anionic Blue-15 with a chemical formula: C42H46N3NaO6S2 and molecular weight: 775.95. This product is commercially available as CI No: 42665. The chemical structure of the Anionic Blue-FFS dye has attributed to Lecotan Blue-AC, Triacid Blue-B, Raviramine Blue-BS and Dinacid Brilliant Blue-B, which is shown in Fig. 1. Synthetic AB-FFS dye solutions were prepared by adding the desired amount of dye in double-distilled water to obtain a stock solution of 1000 mg/L. The working solution was diluted to the required concentration of the experiments.

Fig. 1
figure 1

Structure of anionic blue-FFS dye

Full size image

Preparation of biosorbent

Dried Moringa oleifera seeds were de-shelled and fresh white kernels were washed several times with de-ionized water and air dried. Then, kernels were pulverized and converted into a fine powder with an approximate size range from 300 to 500 µm. MEA were prepared using 2 % of alginate solution was mixed with kernel powder in the ratio of 1:5 to form a suspension solution which was converted into Ca-alginate beads by a phase inversion technique using 3 % of calcium chloride solution with the help of the peristaltic pump. The flow rate of the pump was adjusted to 250 spherical beads per hour. After encapsulation, MEA in the calcium chloride solution was incubated at room temperature for 2 h for stability, which led to the complete replacement of sodium ions by calcium ions. Eventually, the beads were dried and washed with 99 % of ethanol for complete sterilization for storage long periods [9]. In addition, the physical appearances and properties of the MEA have been characterized such as BET surface area, porosity, bulk density and stability as shown in Table 1.

Table 1 The physical appearance and properties of MEA beads
Full size table

Instrumental analysis

The surface morphology of MEA was identified by scanning electron microscopy (SEM) using an Agilent Technology scanning probe microscope. The surface functional groups of MEA were determined by Fourier transform infrared reflection (FTIR) measurements using an ALPHA FT-IR spectrometer. The zeta potential curve of the MEA was analyzed using a (Zetasizer 2000) Malvern Zeta meter.

Batch biosorption studies

Batch biosorption experiments were carried out in 250 ml Erlenmeyer flasks containing 100 ml of AB-FFS initial dye concentrations (25, 50, 75 and 100 mg/L) with the desired amount of MEA (1 g/100 mL). The effect of pH was investigated on the dye in the range of 2–10 pH and the effect of temperature was investigated in the range of 323–343 K. The pH of the solution was adjusted using 0.1 M of HCl and 0.1 M of NaOH solutions. The flasks were agitated in the orbital shaker (Orbitek, Scigenics Biotech) at 100 rpm. Samples were collected at regular intervals. The residual concentration of dyes in the supernatant of each sample was measured using UV–VIS spectrometer at 560 nm using JASCO, UV–670. One set of experiment was conducted using Ca-alginate beads, which is free from M.oleifera. The equilibrium dye adsorbate q e (mg/g) was calculated using the following formula (1):

$$q_{\text{e}} = \left( {C_{\text{o}} - C_{\text{e}} /m} \right)V,$$
(1)

where C o and C e are the initial and final dye concentration in mg/L; V is the volume of the dye solution (L); m is the dry weight of the biosorbent (g).

Fixed bed column studies (FBC)

The fixed bed column reactor was made up of Perspex tubes of 4.5 cm internal diameter and 55 cm in height and the beads (MEA) packed with different heights such as 5, 10 and 15 cm. In this experiment, a known concentration of AB-FFS dye was pumped at different flow rates to a known height of the adsorbent. The particle size of the adsorbent used in the experiment was 2.0 ± 0.1 mm. The samples were collected from the column at regular intervals and the absorbance of the color was measured using a UV–VIS spectrometer at 560 nm. The continuous process flow diagram is shown in Fig. 2.

Fig. 2
figure 2

Continuous process flow diagram

Full size image

Computational statistics and mathematical modeling

Batch experiments were analyzed in triplicate (N = 3) and the data reveals the mean values which represent the error bars. Regression, the correlation coefficient, standard deviation was calculated using SSPC PC + TM statistical package, 1983. Multiple mean comparisons using least significant difference were computed using the significance level (p < 0.05). To investigate the data, two inherent models like Langmuir and Freundlich were used to describe the mechanism of biosorption and to find the maximum biosorption capacity of the adsorbents at different temperatures. The results from the effect of temperature were used to calculate the thermodynamic parameters such as free energy, enthalpy and entropy. Eventually, to access the kinetic parameters, the data with different concentrations results were analyzed using pseudo-first-order, pseudo-second-order and intraparticle diffusion models. To consider, the best fit model to describe the performance of the breakthrough curves, regression coefficients (R 2) can be fit between experimental and theoretical values of Thomas and Yoon–Nelson equations.

Desorption studies

For batch desorption experiments, deionized water and 0.1 M of analytical-grade NH4Cl, EDTA, CH3COOH, HCl, HNO3 and NaOH were used. In this study, a series of 250 ml of Erlenmeyer flasks containing 100 mL of desorption solution was mixed with 10 g of dye-loaded MEA at room temperature. The mixed solution was agitated in an orbital shaker (Orbitek, Scigenics biotech) at 200 rpm for 1 h. The MEA was removed from the solution and centrifuged at 1000 rpm for 5 min and the desorbed concentrations were analyzed using a UV-spectrometer. After each cycling experiments, beads were washed with distilled water thrice and then treated again in 100 mg/L concentration of AB-FFS dye.

Results and discussion

Characterization of biosorbent

The morphology of MEA was investigated before and after biosorption using SEM analysis. From Fig. 3a, the micrograph of dried MEA reveals, the presence of the porous matrix structure which has a rough and a heterogeneous surface area for biosorption. The same bead was examined after biosorption as shown in Fig. 3b. Almost all the porous matrix structures completely disappeared and it clearly depicts that the functional groups present in the MEA provide active sites for AB-FFS to bind and there is much difference in the adsorbent structure (i.e., absence of the porous matrix).The FTIR spectra of MEA before and after biosorption were analyzed as shown in Fig. 3c. A characteristic band at 2902 and 2862 cm−1 is attributed to C–H of CH2 groups of proteins and at 1800–1600 cm−1 is attributed to the C=O bond stretching that defines the presence of a carbonyl group of the fatty acid [12]. The peak that appears at 1627 cm-1 may be attributed to the N-H (amine) groups present in the protein portions of the MEA. On the other hand, an FTIR spectrum of MEA after biosorption shows the disappearance of the two peaks, which is due to the mechanism of cross-linking of MEA which could be either by de-protonation or ionic interaction [9]. In addition, the point of zero charge (pHzpc) was examined for MEA beads, and the results showed that the pHzpc is 4.9–5.1 as shown in Fig. 3d. It can be used to explain the influence of pH on biosorption. When the pH value is lower than pHzpc, the surface charge of the MEA is positive and hence the biosorption capacity decreases. Similarly, the value of pH is greater than pHzpc, and the surface charge of the MEA has a higher neagative charge, which results in higher attraction of the dyes.

Fig. 3
figure 3

SEM images before biosorption (a) and after biosorption (b). c FTIR spectra before and after biosorption. d Zeta potential–pH profile

Full size image

Batch biosorption studies

Effect of initial pH and pHzpc

The pH varies the surface charge properties of the reactant so that the adsorbate or adsorbent can bind to the active site to undergo reactions. The effect of pH on the biosorption capacity of the AB-FFS dye with concentration of 100 mg/L was studied in the range of 2–10. The influence of pH on the biosorption can be explained on the basis of point of zero charge (pHzpc), which is the point at which the net charge of the biosorbent is zero. From Fig. 4a, it can be seen that the degree of AB-FFS biosorption onto MEA decreased from 95.01 to 17.53 % when the pH was increased from 2 to 10. It can be explained by the pHzpc of the adsorbent and the nature of the AB-FFS dye (anionic). The pHzpc of the MEA is around 4.9–5.1, which explains that the surface of the adsorbent is positively charged at under pH 5.1 [9]. At lower pH, large amount of H+ ions is present on the surface of the biosorbents, which favors strong electrostatic attraction and hence maximun rate of biosorption. As the increasing pH (>5) value, the biosorption decreased gradually due to the OH− ions forms the negative charge on the surface of the adsorbents which do not bind to the anionic adsorbate, thus reduces the rate of biosorption due to the electrostatic repulsion [13]. Thus, a maximum AB-FFS biosorption was attained at an optimum pH of 2. Further, the rest of the experiments were conducted at pH 2.

Fig. 4
figure 4

Batch biosorption of AB-FFS onto MEA: a influence of pH (2–10), b influence of initial dye concentrations (25–100 mg/L) and c influence of temperature (323, 333 and 343 K). Experimental conditions: synthetic AB-FFS solution volume: 100 mL; contact time: 8 h; biosorbent mass: 1 g; agitation speed: 100 rpm; Error bars represent SD

Full size image

Effect of initial dye concentration

The study of initial dye concentration influences the performance of MEA and provides information about driving force to overcome all mass transfer resistance between the solid and aqueous phase. The biosorption of AB-FFS concentration was investigated at 25–100 mg/L up to 500 min for all the concentrations using 1.0 g of MEA at room temperature under pH 2. From Fig. 4b, the equilibrium biosorption was observed at 300 min and was found to be a maximum of 98.5 ± 0.5 % for 25 mg/L and minimum of 90.85 ± 1.25 % for 100 mg/L, respectively. At lower AB-FFS concentrations, the dye molecules present in the aqueous solution interacted with the active sites available on the solid surface, facilitating higher biosorption. Consequently, the increase of initial AB-FFS concentration resulted in a reduction of its biosorption percentage due to the limited number of binding sites and more dye molecules were left unabsorbed in the solution resulting in lower rate of biosorption [8, 14].

Effect of temperature and thermodynamic studies

The effect of temperature is an important biosorption parameter to investigate the stability of MEA. From Fig. 4c, it was found that biosorption rate was increased with the increase in temperature. As the temperature increased from 323 to 343 K, it was observed that biosorption porosity increased with a decrease in viscosity of the solution and thereby increased the diffusion rate [8]. Endothermic chemical interaction and disaggregation lead to an increase in temperature. From this experiment, it was found that MEA biosorption was quite good and stable even at higher temperature [15, 16]. Thermodynamic parameters such as Gibbs free energy change (∆G o), standard enthalpy change (∆H o) and standard entropy change (∆S o) are calculated to understand more about the effect of temperature on the biosorption. Biosorption experiments were calculated at different temperatures (323, 333 and 343 K) using the following equations:

$$K_{\text{c}} = C_{\text{a}} /C_{\text{e}} ,$$
(2)
$$\Delta G^\circ = - RT\ln K_{\text{c}} ,$$
(3)
$$\Delta G^\circ = \Delta H^\circ - T\Delta S^\circ ,$$
(4)

where K c is the distribution coefficient for the adsorption; C a is the amount of dye (mg) adsorbed on the adsorbent per liter of the solution at equilibrium and C e is the equilibrium concentration (mg/L) of the dye in the solution. R is the universal gas constant (8.314 J/mol K) and T (°K) the absolute temperature. The standard enthalpy (∆H o) and entropy (∆S o) of adsorption were determined from the Vant Hoff Eq. (5):

$$\ln K_{\text{c}} = [(\Delta S^\circ )/R - \Delta H^\circ /RT].$$
(5)

∆H o and ∆S o were obtained from the slope and intercept of the Vant Hoff plot of lnK c versus 1/T. The values of ∆G o, ∆H o and ∆S o under different temperature are listed in Table 2. The negative values of ∆G o reveal that the biosorbent was spontaneous. The values of Gibbs free energy decreases with an increase in temperature which signifies that MEA is favorable for biosorption. The positive value of ∆H o and ∆S o indicates that the biosorption is an endothermic reaction and there is randomness at the solid–solution interface [17].

Table 2 Thermodynamic parameters of AB-FFS onto MEA at different temperatures
Full size table

Biosorption isotherm modeling

To perform the characterization of the biosorption behavior of the dye, the equilibrium adsorption isotherms on MEA at pH 2 with different temperatures were obtained for the AB-FFS dye. Therefore, these equilibrium data are an essential source for practical design and fundamental understanding behavior of the carrier matrix for MEA. There are few nonlinear regression equations well described by various models. In this study, Langmuir [18] and Freundlich [19] model was chosen and it provides a scrupulously accurate method to reveal the linearity fitting and to explain how the AB-FFS dye interacts with MEA. The equations are listed as follows:

The general form of the Langmuir model is given by

$$C_{\text{e}} / q_{\text{e}} = 1/q_{\hbox{max} } K_{\text{L}} + C_{\text{e}} /q_{\hbox{max} } ,$$
(6)

where q max (mg/g) is the maximum biosorption capacity at equilibrium; K L (L/mg) is the Langmuir binding constant; q e gives the value of the sorbed capacity at equilibrium time (mg/g); C e is the equilibrium concentration of the adsorbed ions (mg/L). The values of q max and K L were estimated from the slope and intercept of the linear plots of C e/q e against C e using values from the batch experiments.

The general form of the Freundlich model is given as

$$\ln \,q_{\text{e}} = \ln \,K_{\text{Fr}} + 1/n \ln C_{\text{e}} ,$$
(7)

where the K Fr (mg 1−1/n L1/n g–1) value gives the relative biosorption capacity of the adsorbent and 1/n is the dimensionless Freundlich adsorption intensity value. The values of K Fr and n can be determined by plotting ln q e versus ln C e resulting in a straight line with a slope of n and an intercept of ln K Fr. A higher value of K Fr estimates provide higher affinity toward the ions and the value of 1/n lies between 0.1 < 1/n < 1 representing favorable biosorption [20].

The detailed parameters of Langmuir and Freundlich isotherm equations are listed in Table 3. From the Langmuir isotherm, the maximum monolayer adsorption capacity of MEA increased from 18.18 to 76.92 (mg/g) with the increase of the solution temperature from 323 to 343 K, respectively, which confirms that the process is an endothermic reaction. The correlation coefficients (R 2) are listed in Table 3, strongly indicating that the biosorption of AB-FFS onto MEA follows both the Langmuir and Freundlich isotherm model.

Table 3 Isotherm parameters for the biosorption of AB-FFS dye onto MEA
Full size table

MEA biosorption was further analyzed in terms of separation factor; R L is a dimensional parameter which is defined as R L = (1/1 + K L C o), derived from the Langmuir equation and C i is the initial dye concentration. R L indicates the biosorption process to be either favorable (0 < R L < 1), unfavorable (R L > 1), linear (R L = 1) or irreversible (R L = 0). From Table 3, R L values gradually increase from 0 to 1, which indicates the process is more favorable, and higher temperature may enhance biosorption process.

Biosorption kinetics modeling

To examine the controlling mechanism of biosorption as well as to understand the behavior of the AB- FFS dye onto the beads, the three kinetics model was investigated: pseudo-first order kinetics, pseudo-second order kinetics followed by Weber and Morris intraparticle diffusion model. In this study, the kinetics of biosorption of two different concentrations of AB-FFS dye (50 and 100 mg/L) onto MEA was carried out with the pseudo-first-order kinetics by Lagergren’s [21] and pseudo-second-order model by Ho and McKay’s [22] followed by Weber and Morris’s intraparticle diffusion model [23].

For the biosorption of AB-FFS, the first-order kinetics can be represented by Eq. 8:

$$\log \,(q_{e} - q_{t} ) = \log \,q_{t} - K_{1} t/2.303,$$
(8)

where q e and q t are the amounts of AB-FFS dye adsorbed (mg/g) at equilibrium and at time t (h), respectively, and K 1 is the adsorption rate constant (min−1). The Lagergren first-order kinetic constant (K 1) and the theoretical value of (q e) can be obtained from the linear plots of log (q e − q t) against time for 50 and 100 mg/L of initial dye concentrations as shown in Fig. 5a. From the Fig. 5a, the plot was found to be linear and the correlation coefficient  (R2) was greater than 0.9, which indicates that  pseudo-first order were appropriate for the use of AB-FFS dye onto MEA. The rate constant (K 1) and q e (exp) values along with the correlation coefficient (R 2) are listed in Table 4. The data was further validated using second-order kinetics, which can be expressed by Eq. 9:

$$t/q_{t} = 1/K_{2} q_{e}^{2} + t/q_{e} .$$
(9)

For the pseudo-second-order kinetic model, the plots of t/q t against time at 50 and 100 mg/L initial dye concentrations are shown in Fig. 5b. The  value  of qe (mg/g) and second-order kinetic constants k2 (g/mg min) along with correlation coefficients of MEA are listed in Table 4. In addition from Table 4, it was noticed that the theoretical predicted q values were not concordant with the experimental values and R 2 values were not in accordance, suggesting that the use of MEA on AB-FFS dye did not fit well with the second-order kinetics. Further, Weber and Morris found a kinetic process of liquid–solid adsorption of intraparticle diffusion and mass action. To identify the diffusion mechanism, the relationship between q t and t 1/2 could be written in the form of Eq. (10) given by:

$$q_{\text{t}} = K_{p} t ^{{\frac{1}{2} }} + C,$$
(10)

where q t (mg/g) is the amount of dye adsorbed at various times (t), K P is the intraparticle diffusion rate constant (mg/g min0.5) and C is the intercept of the line which is directly proportional to the boundary layer of thickness. This multi-linear Eq. 10 involves three steps. The first step is the immediate process that allows quick adsorption, the second step is the intraparticle diffusion stage, whereas the final stage is the equilibrium step in which the solute moves slowly from macropores to micropores causing a slow adsorption rate [8, 22]. A plot of q t against t 1/2 should be linear, from which K P and C can be calculated from the slope and intercept of the plot. According to Weber and Morris, if the intraparticle diffusion is the rate-limiting step, it is necessarily the plot of q versus t 1/2 which passes through the origin.

Fig. 5
figure 5

Pseudo-first-order model (a), Pseudo-second-order model (b) and intraparticle diffusion model (c) for batch adsorption of AB-FFS dye onto MEA. Experimental parameters—dosage 1 g, volume 100 ml, dye concentration 50 and 100 mg/L, temperature 273 K, pH 2, reaction time 500 min

Full size image
Table 4 Kinetic parameters for the biosorption of AB-FFS dye onto MEA
Full size table

The intraparticle diffusion of AB-FFS onto MEA at an initial dye concentration of 50 and 100 mg/L is illustrated in Fig. 5c. It was observed that the straight line of the intraparticle region of MEA of 100 mg/L did not pass through the origin, while the rest pass through the origin. Moreover, it is clear from Table 4 that MEA diffusion of 100 mg/L has a larger intercept C value, which relates high boundary layer resistance and the surface adsorption in the rate-limiting step. According to McKay, the boundary layer thickness retards the intraparticle diffusion. Table 4 clearly explains that the intraparticle parameter K P values increase along with increasing dye concentrations. Thus, the increase of AB-FFS concentrations results in an increase in the diffusion rate of dye into pores of the beads. Especially, MEA increases regularly for 50 mg/L (5.09 mg/g min0.5) and 100 mg/L (9.25 mg/g min0.5) with low K P value.

Fixed bed column study

The performance of the MEA biosorbent was tested in a fixed bed column, to check the feasibility of the MEA in real-time effluents. The AB-FFS solution (100 mg/L) was fed through the column of different bed heights (5 and 15 cm) with two different flow rates (1, 2 and 5 mL/min) and the samples were collected at regular intervals.

Effect of bed height

The effect of bed height is an important parameter for calculating the design of the FBC performance. At a constant initial AB-FFS concentration (100 mg/L) and flow rate (2 mL/min), the breakthrough curve for biosorption of the AB-FFS onto MEA of two different bed heights (BH) such as 5 cm (12.25 g) and 15 cm (36.75 g), respectively, is shown in Fig. 6. From Fig. 6a, both the breakthrough times, t b and exhaustion time t e, were found to increase with increasing bed height, whereas the shape of the breakthrough was slightly different with the variation of bed height. From Fig. 6a, an earlier breakthrough and exhaustion time was attained in BH—5 cm, (t b = 33th min and t e = 340th min) and BH—15 cm (t b = 150th min and t e = 420th min), respectively. An increase in dye uptake was observed at elevated bed height due to the increase in the amount of the MEA. As the bed height increases, simultaneously, the mass transfer zone (MTZ) also increases in the column, which moves downward from the entrance of the bed to the exit.

Fig. 6
figure 6

a Breakthrough curves for biosorption of AB-FFS onto MEA at different bed heights (BH-5 and 15 cm with constant flow rate −2 mL min−1 and initial concentration −100 mg/L). b. Breakthrough curves for biosorption of AB-FFS onto MEA at different flow rates (1, 2 and 5 mL/min with constant BH-15 cm and initial concentration −100 mg/L)

Full size image

Effect of flow rate

The effect of varying flow rate is an important parameter which determines the contact time of the dye with the biosorbent in the FBC. The breakthrough curves Ct/Co against time (min) for three different flow rates (1, 2 and 5 mL/min) with constant bed height of 15 cm were investigated and shown in Fig. 6b. From the figure, as the flow rate increases, the breakthrough curve becomes steeper and the biosorbent achieves early saturation at 5 mL/min. Similarly, at lower flow rate, a longer contact time with the shallow biosorption zone results in a higher uptake of AB-FFS. From Fig. 6b, earlier breakthrough and exhaustion time were attained flow rates (F/R) 1 mL/min (t b = 170th min and t e = 540th min), 2 mL/min (t b = 140th min and t e = 410th min) and 5 mL/min (t b = 10th min and t e = 280th min), respectively.

Modeling of breakthrough curves

Fixed bed column data obtained were further analyzed for their breakthrough behaviors using two different mathematical equation models such as those of Thomas [24] and Yoon–Nelson [25]. The biosorption performance was assessed at an initial concentration ratio, C t/C o > 0.05, consequently, 5 % breakthrough until C t/C o > 0.95 that is, 90 % breakthrough for dye decolorization by considering water quality and operating limits of MTZ of the column [26].

Applications of the Thomas model

The experimental data were fitted to the Thomas model to determine the maximum dye biosorption capacity of the column (q o) and the Thomas rate constant (k Th), as shown in Table 5. Further, this model is based on the assumption that the process follows Langmuir isotherms of equilibrium with no axial dispersion and the rate driving force which obeys the second-order reversible reaction kinetics [27]. The linearized form of Thomas model Eq. (11) can be expressed as follows:

$$\ln \left( {\frac{{C{\text{o}}}}{{C{\text{t}}}} - 1} \right) = \frac{{k_{\text{Th}} \,\;q_{\text{o}} \,\;m}}{v} - \frac{{k_{\text{Th}} \,\;C_{\text{o}} }}{vt},$$
(11)

where k Th (mL/mg/min) is the Thomas rate constant, q o (mg/g) is the equilibrium adsorbate uptake per gram of the biosorbent, C o and C t (mg/L) are the inlet and outlet concentrations (g), m is the mass of the adsorbent in the column, and ν (mL/min) stands for flow rate. The value C t/C o is the ratio of the outlet to inlet effluent concentrations. By plotting the linear plots of ln [(C o/C t) − 1] against time (t), the rate constant value (k Th) was determined and the maximum capacity of biosorption (q o) was obtained from the slope and intercepts using values from the column experiments. The regression coefficient (R 2) and the relative constants such as q o (mg/g) and k Th values were calculated from the experimental data as shown in Table 5. The regression coefficients (R 2) were between 0.8 and 0.9, which showed that the experimental data fitted the Thomas model well. From Table 5, in general, it was observed that by increasing the flow rate, the biosorption capacity (q o) decreased, but the values of the rate constant (k Th) increased. Further, by extending the bed height, the values of q o decreased and the k Th value increased significantly. In addition, from Table 5, it was found that 15 cm of bed height (BH) with 1 mL/min F/R gives maximum biosorption values (q o, 1543 mg/g).

Table 5 Thomas and Yoon–Nelson model parameters for the removal of AB-FFS using MEA at different conditions using linear regression analysis
Full size table

Application of the Yoon–Nelson model

A theoretical model developed by Yoon–Nelson was useful to investigate the breakthrough behavior of AB-FFS on MEA. In addition, this model was derived based on the assumption that the rate of decrease in the probability of biosorption for each adsorbate molecule is proportional to the probability of adsorbate biosorption and the probability of an adsorbate breakthrough on the biosorbent [25, 28]. The linearized model of a single component system is expressed as in Eq. 12:

$$\ln \left( {\frac{{C{\text{t}}}}{{C_{\text{o}} - C_{\text{t}} }}} \right) = k_{\text{YN}} \,\;t - \tau \,k_{\text{YN}} ,$$
(12)

where, k YN (1/min) is the Yoon–Nelson rate constant and τ (min) is the time required for 50 % adsorbate breakthrough. The values of k YN and τ were estimated from the slope and intercepts of the linear graph between ln [(C t)/(C o − C t)] versus time t at different flow rates with different bed heights and the values of k YN and τ are illustrated in Table 5. From Table 5, the values of k YN were found to increase with higher F/R and lower BH; however, it decreased with lower F/R and higher BH. Nevertheless, τ (the time required for 50 % breakthrough) was higher at lower F/R and higher BH. In addition, from Table 3, it was found that the τ (min) values of 205 min and 223 min were obtained at 15 BH with F/R 1 mL/min and 15 BH with F/R 2 mL/min. The values of the regression coefficient (R2) are listed in Table 5 and it was found that almost all the values of R 2 were between the range of 0.8 and 0.9. Furthermore, there is good concurrence between the predicted and experimental data which provide the best fit to the Yoon–Nelson model.

Desorption studies

To improve the cost-effectiveness in industries, reusability of the biosorbent is an important factor in practical applications for dye removal from wastewaters. The reusability of MEA beads can be determined by its biosorption performance in consecutive biosorption/resorption cycles under batch mode and the desorption efficiencies are compared in Fig. 7. From the figure, the use of deionized water was found to be negligible (<5 %). Further, the use of NH4Cl was resorbed by only <20 %, whereas CH3COOH and EDTA give 50–60 % of the desorption efficiency. The use of acids such as HNO3 and HCl gives more than 90 % de-resorption efficiency which can be attributed to the fact that the AB-FFS dyes react faster with acids than bases. On the other hand, during the desorption process, NaOH reacts with calcium-alginate beads and it was completely dissolved due the replacement of calcium and sodium ions. Overall, HNO3 and HCl was found to have higher resorption efficiencies and similar work has been reported previously [29, 30]. The overall MEA adsorbent was found to be cost-effective and feasible for treatment of industrial wastewater treatment.

Fig. 7
figure 7

Desorption efficiency of AB-FFS dye onto MEA using different desorbing agents (concentration: 0.1 M)

Full size image

Conclusion

This research work introduced the encapsulated Moringa oleifera beads as a potential biosorbent for dye removal in the batch as well as in continuous column studies which gave more than 90 % of removal efficiency. The maximum biosorption capacity of AB-FFS dye calculated from Langmuir isotherm, which can be well fitted onto MEA of 18.18, 23.80 and 76.92 mg/g, respectively, was studied from 323 to 343 K. The thermodynamic parameter results reveal that the biosorbent was spontaneous and it was an endothermic reaction process. Among the kinetic model studies, the biosorption kinetics favor both pseudo-first-order and intraparticle diffusion model. In fixed bed column studies, data obtained were fitted with well-established models, namely Thomas and Yoon–Nelson. Overall, this research showed that MEA is a potential and promising alternative biosorbent for removal of color from textile effluents. Moreover, dried Moringa oleifera is a biological waste material that is easily viable and biodegradable.