1 Introduction

The interaction between plants and herbivores is a fascinating and complex aspect of ecology. Herbivores rely on plants as a source of food, while plants depend on herbivores to disperse their seeds and pollinate their flowers. These interactions play a critical role in shaping the structure and function of many ecosystems. However, the dynamics of plant–herbivore systems can be challenging to understand due to the complexity of the ecological relationships involved [1, 2].

To gain insights into the mechanisms that govern the dynamics of plant–herbivore interactions, researchers have developed mathematical models that capture the essential features of these systems. Mathematical modeling allows scientists to investigate the behavior of complex ecological systems under different scenarios and to explore how changes in key variables can impact the long-term sustainability of ecosystems [3].

One commonly used approach in modeling plant–herbivore interactions is to use continuous-time models. These models describe the dynamics of the populations as a set of differential equations, which can be solved numerically to obtain insights into the behavior of the system over time. However, continuous-time models can be challenging to analyze due to their complexity, and it can be challenging to obtain analytical results that provide insights into the behavior of the system.

To overcome these challenges, researchers have developed discrete-time models that allow them to study the dynamics of plant–herbivore systems over discrete time steps. Discrete-time models are obtained by discretizing the continuous-time model using various approximation methods, such as piecewise constant argument. Piecewise constant argument allows us to study the behavior of the system over discrete time steps and to investigate the effects of different parameter values and initial conditions on the dynamics of the populations. Moreover, the use of piecewise constant argument can be computationally efficient and may provide insights into the underlying mechanisms that drive the dynamics of the system [4].

Discrete-time models can capture a wide range of dynamical behaviors, including stable equilibria, limit cycles, and chaotic attractors. Moreover, discrete-time models can be more amenable to mathematical analysis, making it easier to obtain analytical results that provide insights into the behavior of the system.

One key advantage of discrete-time models is that they allow researchers to investigate the effects of different parameter values and initial conditions on the behavior of the system. Parameter values represent the biological or environmental factors that impact the dynamics of the populations, while initial conditions represent the starting populations of plants and herbivores. By varying the parameter values and initial conditions, researchers can investigate how changes in these variables can impact the behavior of the system over time.

Another advantage of discrete-time models is that they can be used to investigate the sensitivity of the system to changes in key parameters. Sensitivity analysis is an essential tool for understanding the robustness of ecological systems and for identifying critical thresholds beyond which the system may become unstable or exhibit unexpected behavior. By performing sensitivity analysis on the discrete-time plant–herbivore model, researchers can identify the critical parameters that impact the dynamics of the system and investigate how changes in these parameters can lead to shifts in the behavior of the system.

In addition to using the piecewise constant argument to discretize the continuous-time model, we also substitute the logistic growth function commonly used in such models with the Ricker map to simulate the plant population’s growth. The Ricker map is a discrete-time dynamical system that has been widely utilized in ecology to model population dynamics [1]. It can capture a diverse range of dynamic behaviors, including stable equilibria, limit cycles, and chaotic attractors. Additionally, the Ricker map is more mathematically tractable than the logistic growth function, making it easier to obtain analytical results for the plant–herbivore system’s behavior. By replacing the logistic growth function with the Ricker map, we can develop a more manageable model that still retains the crucial aspects of plant growth and reproduction [5,6,7,8].

In this paper, we present a qualitative analysis of a discrete-time plant–herbivore model based on a set of difference equations. We investigate the behavior of the model under different parameter values and initial conditions, focusing on the emergence of stable equilibria, period doubling, and chaotic attractors. Our analysis reveals that the model exhibits a range of interesting dynamical behaviors and is highly sensitive to changes in key parameters. We discuss the implications of these findings for our understanding of plant–herbivore systems and highlight the importance of qualitative analysis in providing insights into the behavior of complex ecological systems.

The rest of the paper is organized as follows. In Sect. 2, we examine the equilibrium points’ stability in the proposed model. Section 3 details the bifurcation analysis, with emphasis on the emergence of distinct dynamic behaviors and their sensitivity to changes in parameter values. We provide details on the numerical simulations we conducted to examine the model’s behavior under various circumstances in Sect. 4. Finally, we summarize our primary findings in Sect. 5 as we conclude the paper.

Consider the plant–herbivore model

$$\begin{aligned} \begin{aligned} \frac{\textrm{d} x}{\textrm{d} t}&=r x\textrm{e}^{\left( 1-x\right) }-\frac{x^{2}y}{1+x}, \\ \frac{\textrm{d} y}{\textrm{d} t}&=\frac{x y}{1+x}-\alpha y. \end{aligned} \end{aligned}$$
(1)

The model consists of two variables, namely x(t) and y(t), representing the population size of the plant and herbivore at a specific time t. The intrinsic growth rate of the plant is denoted by the parameter r, while the herbivore’s death rate is represented by \(\alpha \), with both parameters having positive values.

By assuming that the variables and functions change only at fixed time intervals, Eq. (1) can be transformed into a system of equations utilizing the greatest integer function [t], as demonstrated in [4]:

$$\begin{aligned} \begin{aligned} \frac{1}{x(t)}\frac{\textrm{d} x(t)}{\textrm{d} t}&=r \textrm{e}^{\left( 1-x[t]\right) }-\frac{x[t]y[t]}{1+x[t]}, \\ \frac{1}{y(t)}\frac{\textrm{d} y(t)}{\textrm{d} t}&=\frac{x[t]}{1+x[t]}-\alpha . \end{aligned} \end{aligned}$$
(2)

The use of the piecewise constant argument [t] for this conversion enables the solution of all differential equations in Eq. (2) through direct integration over a time interval of unit length. This is achievable because all variables and functions on the right-hand side of Eq. (2) remain constant throughout the interval. Consequently, integrating the system (2) over the interval \([n, n+1)\) yields:

$$\begin{aligned} \begin{aligned} \ln \frac{x({n+1})}{x(n)}&=r \textrm{e}^{\left( 1-x(n)\right) }-\frac{x(n) y(n)}{1+x(n)}, \\ \ln \frac{y(n+1)}{y(n)}&=\frac{x(n)}{1+x(n)}-\alpha , \end{aligned} \end{aligned}$$
(3)

for \(n = 0, 1, 2, \cdot \cdot \cdot \)

To simplify the notation, we can define x(n) as \(x_n\) and y(n) as \(y_n\). Utilizing this notation, we obtain the following discrete-time model:

$$\begin{aligned} \begin{aligned} x_{n+1}&=x_{n} \textrm{e}^{\big ( r \textrm{e}^{\left( 1-x_{n}\right) }-\frac{x_n y_{n}}{1+x_n}\big )}, \\ y_{n+1}&=y_{n} \textrm{e}^{\big ( \frac{x_n}{1+x_n}-\alpha \big )}. \end{aligned} \end{aligned}$$
(4)

It is assumed that the initial values of the solutions for system (4) satisfy \(x_0 > 0\) and \(y_0 > 0\). Moreover, it can be proven that if the initial values \(x_0\) and \(y_0\) are positive for system (4), the resulting solutions \(x_n\) and \(y_n\) will also be positive.

The fixed points, which correspond to the steady states of the population model represented by Eq. (4), can be identified by solving the algebraic system:

$$\begin{aligned} \begin{aligned} x&=x \textrm{e}^{\big ( r \textrm{e}^{\left( 1-x\right) }-\frac{xy}{1+x}\big )}, \\ y&=y\textrm{e}^{\big ( \frac{x}{1+x}-\alpha \big )}. \end{aligned} \end{aligned}$$
(5)

The fixed points of the system (4) are \(E_0(0,0)\) and \(E_1(\frac{\alpha }{1-\alpha },\frac{r}{\alpha }e^{\frac{2\alpha -1}{\alpha -1}})\). The fixed point \(E_0\) exists for all parameter values, while \(E_1\) exists only when \(\alpha <1\). Assuming \(x_0>0\) and \(y_0>0\) for the system in Eq. (4), it can be shown that \(x_n\) and \(y_n\) are positive for all \(n\ge 0\).

In terms of biology, \(E_0\) corresponds to a state where there are no plants or herbivores present, while \(E_1\) represents a stable coexistence of non-zero populations of plants and herbivores.

2 The stability of equilibrium

The focus of this section is to analyze the local stability of the equilibria of system (4). To accomplish this, we will calculate the Jacobian matrix of the system at a given state variable, which is given by:

$$\begin{aligned} J(x,y)=\left( \begin{array}{cc} -\frac{\left( x r(1+x)^2 \textrm{e}^{1-x}-1-x^2+(y-2) x\right) \textrm{e}^{r \textrm{e}^{1-x}-\frac{x y}{1+x}}}{(1+x)^2} &{} -\frac{x^2 \textrm{e}^{r \textrm{e}^{1-x}-\frac{x y}{1+x}}}{1+x} \\ \frac{y \textrm{e}^{\frac{x}{1+x}-\alpha }}{(1+x)^2} &{} \textrm{e}^{\frac{x}{1+x}-\alpha } \end{array} \right) . \end{aligned}$$
(6)

The characteristic equation associated with the Jacobian matrix (6) is:

$$\begin{aligned} {\nu }^{2}-a(x,y)\nu +b(x,y)=0, \end{aligned}$$
(7)

where

$$\begin{aligned} \begin{aligned} a(x,y)&=-\frac{\left( x r(1+x)^2 \textrm{e}^{1-x}-1-x^2+(y-2) x\right) \textrm{e}^{r \textrm{e}^{1-x}-\frac{x y}{1+x}}}{(1+x)^2}+\textrm{e}^{\frac{x}{1+x}-\alpha },\\ b(x,y)&=-\frac{\left( r x(1+x)^3 \textrm{e}^{1-x}-1-x^3-3 x^2+(y-3) x\right) \textrm{e}^{\frac{r(1+x) \textrm{e}^{1-x}+(-y-\alpha +1) x-\alpha }{1+x}}}{(1+x)^3}. \end{aligned} \end{aligned}$$
(8)

Prior to analyzing the stability of the equilibrium points of system (4), it is necessary to introduce the following definition and lemma:

Definition 2.1

Let E(x, y) be a fixed point of the system (4), and let \(\nu _1\) and \(\nu _2\) be the eigenvalues of the Jacobian matrix evaluated at E.

  1. (i)

    E is called a sink (locally asymptotically stable) if \(\mid \nu _1\mid < 1\) and \(\mid \nu _2\mid < 1\);

  2. (ii)

    E is called a source if \(\mid \nu _1\mid > 1\) and \(\mid \nu _2\mid > 1\). A source is locally unstable;

  3. (iii)

    E is called a saddle if \(\mid \nu _1\mid < 1\) and \(\mid \nu _2\mid > 1\) (or \(\mid \nu _1\mid > 1\) and \(\mid \nu _2\mid < 1\));

  4. (iv)

    E is called non-hyperbolic if either \(\mid \nu _1\mid =1\) and \(\mid \nu _2\mid = 1\).

Lemma 2.2

Let \(R(\nu ) = \nu ^2 + a\nu + b\). Suppose that \(R(1) > 0\), \(\nu _1\) and \(\nu _2\) are the roots of \(R(\nu ) = 0\). Then

  1. (i)

    \(\mid \nu _1\mid < 1\) and \(\mid \nu _2\mid < 1\) if and only if \(R(-1) > 0\) and \(b < 1\);

  2. (ii)

    \(\mid \nu _1\mid < 1\) and \(\mid \nu _2\mid > 1\) (or \(\mid \nu _1\mid > 1\) and \(\mid \nu _2\mid < 1\)) if and only if \(R(-1) < 0\);

  3. (iii)

    \(\mid \nu _1\mid > 1\) and \(\mid \nu _2\mid > 1\) if and only if \(R(-1) > 0\) and \(b > 1\);

  4. (iv)

    \(\nu _1 =-1\) and \(\mid \nu _2\mid \ne 1\) if and only if \(R(-1) = 0\) and \(b \ne 0,2\);

  5. (v)

    \(\nu _1\) and \(\nu _2\) are complex and \(\nu _1 =\mid \nu _2\mid = 1\) if and only if \(a^2-4b < 0\) and \(b = 1\).

In the following, we will examine the stability of the equilibrium point \(E_0\) in the system (4).

Proposition 2.3

The equilibrium point \(E_0\) of system (4) is always a saddle.

Proof

The expression for the Jacobian matrix of (4) evaluated at \(E_{0}\) is denoted as \(J\left( E_{0}\right) \) and is given by:

$$\begin{aligned} J(E_{0})=\left( \begin{array}{cc} \textrm{e}^{r \textrm{e} } &{} 0 \\ 0 &{} \textrm{e}^{-\alpha } \end{array} \right) , \end{aligned}$$

and the eigenvalues of \(J\left( E_{0}\right) \) are

$$\begin{aligned} \nu _1=\textrm{e}^{r \textrm{e} }>1, \quad \nu _2=\textrm{e}^{-\alpha }<1. \end{aligned}$$

Thus, \(E_0\) is a saddle point since \(\left| \nu _1\right| >1,\left| \nu _2\right| <1\). \(\square \)

The Jacobian matrix of the system (4) evaluated at the fixed point \(E_1\) is denoted by \(J(E_1)\), and it is given by:

$$\begin{aligned} J(E_{1})=\left( \begin{array}{cc} \frac{r\left( \alpha ^2-\alpha +1\right) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}+\alpha -1}{\alpha -1} &{} \frac{\alpha ^2}{\alpha -1} \\ \frac{r \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}(\alpha -1)^2}{\alpha } &{} 1 \end{array} \right) , \end{aligned}$$

whereas its characteristic polynomial can be computed as:

$$\begin{aligned} R(\nu )= {\nu }^{2}-\left( \frac{r\left( \alpha ^2-\alpha +1\right) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}} }{\alpha -1} +2\right) \nu +\frac{-r\left( \alpha ^3-3 \alpha ^2+2 \alpha -1\right) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}}{\alpha -1}+1. \end{aligned}$$
(9)

Furthermore, we can obtain more information about the stability of \(E_1\) by evaluating \(R(\nu )\) at specific values of \(\nu \). Specifically, we have:

  • \(R(1) =\alpha r (1-\alpha ) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}\),

  • \(R(-1) =4-\frac{r\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}}{\alpha -1}\), and

  • \(R(0)=1-\frac{r\left( \alpha ^3-3 \alpha ^2+2 \alpha -1\right) \textrm{e}^{\frac{2 \alpha -1}{\alpha -1}}}{\alpha -1}\).

The values obtained from evaluating \(R(\nu )\) at specific values of \(\nu \) can be utilized to determine the stability of \(E_1\) and offer understanding into the behavior of the system in the vicinity of this fixed point.

Proposition 2.4

Considering the fixed point \(E_{1}\) of system (4), we can make the following conclusions about its stability:

  1. (i)

    \(E_{1}\) is sink if \(r<\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\);

  2. (ii)

    \(E_{1}\) is a saddle if \(r>\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\);

  3. (iii)

    \(E_{1}\) is never a source;

  4. (iv)

    \(E_{1}\) loses stability via a flip point when \(r=\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\);

  5. (v)

    \(E_1\) cannot lose stability via a Neimark–Sacker point.

Proof

Using Lemma 2.2, we can obtain the results of this proposition. \(\square \)

Fig. 1
figure 1

Stability regions of fixed point \(E_{1}\) in (\(\alpha ,r\))-space

Full size image

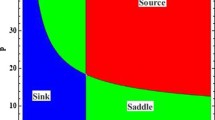
The stability regions for \(E_{1}\), obtained in Proposition 2.4, are depicted in Fig. 1.

3 Bifurcations analysis

This section examines the occurrence of bifurcation near equilibria, based on the theoretical research discussed in Sect. 2. As is commonly known, the classification of bifurcation types is primarily determined by the properties of the eigenvalues surrounding the equilibrium points.

The subsequent discussion concerns the presence of bifurcation around the equilibria \(E_{1}\) and outlines the prerequisites for a period-doubling bifurcation to occur. Specifically, if condition (iv) from Proposition 2.4 is satisfied, one of the eigenvalues of \(J_{E_{1}}\) around \(E_{1}\) equals \(-1\), while the other eigenvalue is not equal to 1 or \(-1\). Under these conditions, a period-doubling bifurcation arises from a small parameter neighborhood centered at \(r=\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\) as the parameter is varied. This neighborhood of parameters are defined by the set

$$\begin{aligned} P_{E_{1}}=\left\{ \left( \alpha , r\right) : r=\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\quad \right\} . \end{aligned}$$

3.1 Period-doubling bifurcation

The focus of this section is to study the period-doubling bifurcation of model (4) at \(E_{1}\) in a small neighborhood of \(P_{E_{1}}\), by analyzing the dynamics of arbitrary parameters \(\left( r^{*},\alpha \right) \) chosen from \(P_{E_{1}}\). By considering \(r^{*}\) as a new dependent variable, we can derive

$$\begin{aligned} \begin{aligned} x_{n+1}&=x_{n} \textrm{e}^{\big ( \left( r+r^{*}\right) \textrm{e}^{\left( 1-x_{n}\right) }-\frac{x_n y_{n}}{1+x_n}\big )}, \\ y_{n+1}&=y_{n} \textrm{e}^{\big ( \frac{x_n}{1+x_n}-\alpha \big )}. \end{aligned} \end{aligned}$$
(10)

We can convert the equilibrium point \(E_{1}\) of the discrete-time model (10) into the origin O(0, 0) by defining \(u_{n}=x_{n}-x^{*}\) and \(v_{n}=y_{n}-y^{*}\). After some calculations, we obtain

$$\begin{aligned} \left. \begin{aligned} u_{n+1}&={\phi _{11}} u_{n}+{\phi _{12}} v_{n}+{\phi _{13}} u_{n}^{2}+{\phi _{14}} u_{n} v_{n} +{\phi _{15}} v_{n}^{2}+\Upsilon _{01} u_{n} r^{*}+\Upsilon _{02} v_{n} r^{*}\\ {}&+O\left( \left| u_{n}\right| ,\left| v_{n}\right| ,\left| r^{*}\right| \right) ^{3}, \\ v_{n+1}&={\phi _{21}} u_{n}+{\phi _{22}} v_{n}+{\phi _{23}} u_{n}^2+{\phi _{24}} u_{n} v_{n}+O\left( \left| u_{n}\right| ,\left| v_{n}\right| \right) ^{3}, \end{aligned} \right\} \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned}&{\phi _{11}}=-\frac{\left( r x(x+1)^2 \textrm{e}^{1-x}-1-x^2+x(y-2) \right) \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x y}{x+1}}}{(x+1)^2}, \quad {\phi _{12}}=-\frac{x^2 \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x y}{x+1}}}{x+1},\\ {}&{\phi _{13}}=\frac{\left( \left( x^3-2+(2 y-3) x\right) (x+1)^2 r \textrm{e}^{1-x}+r^2 x(x+1)^4 \textrm{e}^{-2 x+2}+(-2+(y-2) x) y\right) \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x y}{x+1}}}{2(x+1)^4},\\ {}&{\phi _{14}}=\frac{x\left( r x(x+1)^2 \textrm{e}^{1-x}-2-x^2+(y-3) x\right) \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x y}{x+1}} }{(x+1)^3}, \quad {\phi _{15}}= \frac{x^3 \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x y}{x+1}}}{2(x+1)^2}, \\ {}&\Upsilon _{01}=-\frac{\left( r x(x+1)^2 \textrm{e}^{1-x}-1+x^3+x^2+(y-1) x\right) \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x^2-x y+1}{x+1}}}{(x+1)^2}, \quad \Upsilon _{02}=-\frac{x^2 \textrm{e}^{\frac{r(x+1) \textrm{e}^{1-x}-x^2-x y+1}{x+1}}}{x+1},\\ {}&{\phi _{21}}=\frac{y \textrm{e}^{-\frac{\alpha x+\alpha -x}{x+1}}}{(x+1)^2}, \quad {\phi _{22}}=\textrm{e}^{-\frac{\alpha x+\alpha -x}{x+1}}, \quad {\phi _{23}}=-\frac{y \textrm{e}^{-\frac{\alpha x+\alpha -x}{x+1}}(2 x+1)}{2(x+1)^4}, \quad {\phi _{24}}=\frac{\textrm{e}^{-\frac{\alpha x+\alpha -x}{x+1}}}{(x+1)^2}. \end{aligned} \end{aligned}$$

It is now possible to construct an invertible matrix T by:

$$\begin{aligned} T=\left( \begin{array}{cc} {\phi _{12}} &{} {\phi _{12}} \\ -1-{\phi _{11}} &{} \lambda _{2}-{\phi _{11}} \end{array} \right) ; \end{aligned}$$

we can then utilize the translation

$$\begin{aligned} \left( \begin{array}{c} u_{n} \\ v_{n} \end{array} \right) =\left( \begin{array}{cc} {\phi _{12}} &{} {\phi _{12}} \\ -1-{\phi _{11}} &{} \lambda _{2}-{\phi _{11}} \end{array} \right) \left( \begin{array}{c} X_{n} \\ Y_{n} \end{array} \right) . \end{aligned}$$

(11) gives

$$\begin{aligned} \left( \begin{array}{c} X_{n+1} \\ Y_{n+1} \end{array} \right) =\left( \begin{array}{cc} -1 &{} 0 \\ 0 &{} \lambda _{2} \end{array} \right) \left( \begin{array}{l} X_{n} \\ Y_{n} \end{array} \right) +\left( \begin{array}{l} {\phi }\left( u_{n}, v_{n}, r^{*}\right) \\ {\widehat{\Psi }}\left( u_{n}, v_{n}, r^{*}\right) \end{array} \right) , \end{aligned}$$
(12)

where

$$\begin{aligned} \begin{aligned} {\phi }(u_{n}, v_{n}, r^{*})=&\frac{{\phi _{13}}\lambda _{2}-{\phi _{13}}{\phi _{11}}-{\phi _{12}}{\phi _{23}}}{{{\phi _{12}}(1+\lambda _{2})}} u_{n}^{2} +\frac{{\phi _{14}}(\lambda _{2}-{\phi _{11}})-{\phi _{12}} {\phi _{24}}}{{\phi _{12}}(1+\lambda _{2})} u_{n} v_{n}+\frac{\Upsilon _{01}(\lambda _{2}-{\phi _{11}})}{ {\phi _{12}}(1+\lambda _{2})} u_{n} r^{*}\\ {}&+\frac{\Upsilon _{02}(\lambda _{2}-{\phi _{11}})}{ {\phi _{12}}(1+\lambda _{2})} v_{n} r^{*}+\frac{{\phi _{15}}(\lambda _{2}-{\phi _{11}})}{ {\phi _{12}}(1+\lambda _{2})} v_{n}^{2} +O(|u_{n}|,|v_{n}|,|r^{*}|)^{3},\\ {\widehat{\Psi }}(u_{n}, v_{n}, r^{*})=&\frac{{\phi _{13}}(1+{\phi _{11}})+{\phi _{12}}{\phi _{23}}}{{\phi _{12}}(1+\lambda _{2})} u_{n}^{2}+\frac{{\phi _{14}}(1+{\phi _{11}})+{\phi _{12}}{\phi _{24}}}{{\phi _{12}}(1+\lambda _{2})}u_{n}v_{n}+\frac{\Upsilon _{01}(1+{\phi _{11}})}{{\phi _{12}}(1+\lambda _{2})} u_{n} r^{*}\\ {}&+\frac{\Upsilon _{02}(1+{\phi _{11}})}{{\phi _{12}}(1+\lambda _{2})} v_{n} r^{*}+\frac{{\phi _{15}}(1+{\phi _{11}})}{ {\phi _{12}}(1+\lambda _{2})} v_{n}^{2}+O(|u_{n}|,|v_{n}|,|r^{*}|)^{3},\\ \end{aligned} \\ \begin{aligned} u_{n}^{2}=&{\phi _{12}}^{2}\left( X_{n}^{2}+2 X_{n} Y_{n}+Y_{n}^{2}\right) , \\ u_{n}v_{n}=&-{\phi _{12}}(1+{\phi _{11}}) X_{n}^{2}+\left( {\phi _{12}}(\lambda _{2}-{\phi _{11}})-{\phi _{12}}(1+{\phi _{11}}) \right) X_{n} Y_{n} +{\phi _{12}}\left( \lambda _{2}-{\phi _{11}}\right) Y_{n}^{2}, \\ u_{n} r^{*}=&{\phi _{12}} X_{n} r^{*}+{\phi _{12}} Y_{n} r^{*}, \\ u_{n}^{2} r^{*}=&{\phi _{12}}^{2}\left( X_{n}^{2} r^{*}+2 X_{n} Y_{n} r^{*}+Y_{n}^{2} r^{*}\right) . \end{aligned} \end{aligned}$$

Next, we aim to find the center manifold \(W^{c}(0,0)\) of (12) in a narrow parameter range around \(r^{*}\) [9,10,11,12]. According to the center manifold theorem, we can express the center manifold \(W^{c}(0,0)\) as follows:

$$\begin{aligned} W^{c}(0,0)=\left\{ \left( X_{n}, Y_{n}\right) : Y_{n}=c_{0} r^{*}+c_{1} X_{n}^{2}+c_{2} X_{n} r^{*}+c_{3} (r^{*})^{ 2}+O\left( \left( \left| X_{n}\right| ,\left| r^{*}\right| \right) ^{3}\right) \right\} , \end{aligned}$$

where \(O\left( \left( \left| X_{n}\right| +\left| r^{}\right| \right) ^{3}\right) \) denotes a function that has at least third-order terms in the variables \(\left( X_{n}, r^{}\right) \), and

$$\begin{aligned} \begin{aligned}&c_{0}=0, \\&c_{1}=\frac{{\phi _{12}}{\phi _{14}}(1+{\phi _{11}})^2-{\phi _{23}}{\phi _{12}}^3-{\phi _{12}}^2({\phi _{13}}-{\phi _{24}})(1+{\phi _{11}})-{\phi _{15}}(1+{\phi _{11}})^3}{{\phi _{12}}(\lambda _{2}^{2}-1)}, \\&c_{2}=-\frac{(1+{\phi _{11}})\big ({\phi _{12}}\Upsilon _{01}-\Upsilon _{02}(1+{\phi _{11}})\big )}{(1+\lambda _{2})^{2}}, \\ {}&c_{3}=0. \end{aligned} \end{aligned}$$

Therefore, we can study the map (12) on \(W^{c}(0,0)\) as follows:

$$\begin{aligned} f\left( X_{n}\right) =-X_{n}+h_{1} X_{n}^{2}+h_{2} X_{n} r^{*}+h_{3} X_{n}^{2} r^{*}+h_{4} X_{n} (r^{*})^{2}+h_{5} X_{n}^{3}+O\left( \left( \left| X_{n}\right| ,\left| r^{*}\right| \right) ^{4} \right) , \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{aligned} h_{1}=&\frac{1}{{\phi _{12}}(1+\lambda _{2})}\Big [\big ({\phi _{12}}{\phi _{14}}+{\phi _{15}}(\lambda _2-2) \big ){\phi _{11}}^2+\big (({\phi _{24}}-{\phi _{13}}){\phi _{12}}^2-{\phi _{14}}{\phi _{12}}(\lambda _2-1)+2\lambda _2{\phi _{15}}\\ {}&-{\phi _{15}} \big ){\phi _{11}}-{\phi _{23}}{\phi _{12}}^3+({\phi _{24}}+\lambda _2{\phi _{13}}){\phi _{12}}^2-\lambda _2{\phi _{12}}{\phi _{14}}+\lambda _2{\phi _{15}}-{\phi _{15}}{\phi _{15}}\Big ], \\ h_{2}=&\frac{(\lambda _2-{\phi _{11}})(\Upsilon _{01}{\phi _{12}}-\Upsilon _{02}(1+{\phi _{11}}))}{{\phi _{12}}(1+\lambda _{2})}, \end{aligned} \\ \begin{aligned} h_{3}=&\frac{1}{{\phi _{{12}}}^{2} (\lambda _{{2}}+1 ) ^{3} ( \lambda _{{2}}-1) } \Big [ -\Upsilon _{{01}}\phi _{{23}} \big ( ( 1-3\,\lambda _{{2}} ) \phi _{{11}}+\lambda _{{2}}^{2}-\lambda _{{2}}+2 \big )\phi _{{12}}^{4}+ \big ( -3\, \big ( \phi _{{23}}\Upsilon _{{02}}\\&+\Upsilon _{{01}} \left( \phi _{{24}}-\phi _{{13}} \right) \big ) ( \lambda _{{2}}-\frac{1}{3}) {\phi _{{11}}}^{2}+ \big ( ( 2\,\phi _{{23}}\Upsilon _{{02}}+2\,\Upsilon _{{01}} ( \phi _{{24}}-\frac{3}{2}\,\phi _{{13}} ) ) {\lambda _{{2}}}^{2}+ \big ( -2\,\phi _{{23}}\Upsilon _{{02}}\\ {}&-4\,\Upsilon _{{01}} \left( \phi _{24}-\phi _{{13}} \right) \big ) \lambda _{{2}}+4\,\phi _{{23}}\Upsilon _{{02}}+2\,\Upsilon _{{01}} ( \phi _{{24}}-\frac{1}{2}\,\phi _{{13}} ) \big ) \phi _{{11}}-{\lambda _{{2}}}^{3}\Upsilon _{{02}}\phi _{{23}}+ \big ( -\phi _{{23}}\Upsilon _{{02}}\\&+2\,\Upsilon _{{01}} ( \phi _{{24}}-\frac{3}{2}\,\phi _{{13}} ) \big ) {\lambda _{{2}}}^{2}+ \big ( -2\,\phi _{{23}}\Upsilon _{{02}}-\Upsilon _{{01}} \left( \phi _{{24}} -\phi _{{13}}\right) \big ) \lambda _{{2}}+\phi _{{24}}\Upsilon _{{01}}+2\,\phi _{{23}}\Upsilon _{{02}} \big ) {\phi _{{12}}}^{3}\\&+ \Big ( 3\, \big ( \left( \phi _{{24}}-\phi _{{13}} \right) \Upsilon _{{02}}-\Upsilon _{{01}}\phi _{{14}} \big ) ( \lambda _{{2}}-\frac{1}{3} ) {\phi _{{11}}}^{2}+ \left( \big ( \left( 4\,\phi _{{13}}-3\,\phi _{{24}} \right) \Upsilon _{{02}}+4\,\Upsilon _{{01}}\phi _{{14}} \right) {\lambda _{{2}}}^{2} \\&+\big ( \left( 2\,\phi _{{24}}-2\,\phi _{{13}} \right) \Upsilon _{{02}}-4\,\Upsilon _{{01}}\phi _{{14}} \big ) \lambda _{{2}}-3\,( \phi _{{24}}-\frac{2}{3}\,\phi _{{13}} ) \Upsilon _{{02}} \big ) \phi _{{11}}+ \big ( \left( -\phi _{{13}}+\phi _{{24}} \right) \Upsilon _{{02}}\\ {}&-\Upsilon _{{01}}\phi _{{14}} \big ) {\lambda _{{2}}}^{3}+ \left( 3\,\Upsilon _{{01}}\phi _{{14}}+\Upsilon _{{02}} \phi _{{13}} \right) {\lambda _{{2}}}^{2}+2\, \left( \phi _{{24}} -\phi _{{13}} \right) \Upsilon _{{02}}\lambda _{{2}}-\phi _{{24}}\Upsilon _{{02}} \Big ) \left( 1+\phi _{{11}} \right) {\phi _{{12}}}^{2}\\&+2\, \big ( -\frac{3}{2}\, \left( \Upsilon _{{01}}\phi _{{15}}+\Upsilon _{{02}}\phi _{{14}} \right) ( \lambda _{{2}}-\frac{1}{3} ) \phi _{{11}}+ \left( \Upsilon _{{01}}\phi _{{15}}+\Upsilon _{{02}}\phi _{{14}} \right) {\lambda _{{2}}}^{2}+ ( -\frac{3}{2}\,\Upsilon _{{01}}\phi _{{15}}\\&-\frac{1}{2}\,\Upsilon _{{02}}\phi _{{14}} ) \lambda _{{2}}-\frac{1}{2}\,\Upsilon _{{01}}\phi _{{15}}+\frac{1}{2}\,\Upsilon _{{02}}\phi _{{14}} \big ) \left( 1+\phi _{{11}} \right) ^{2} \left( \lambda _{{2}}-\phi _{{11}} \right) \phi _{{12}}-3\,\phi _{{15}}\Upsilon _{{02}} ( \lambda _{{2}}-\frac{1}{3} )\\ {}&\left( 1+\phi _{{11}} \right) ^{3} \left( \lambda _{{2}}-\phi _{{11}} \right) ^{2} \Big ], \end{aligned} \\ \begin{aligned} h_{4}=&-{\frac{\left( 1+ \phi _{{11}} \right) \left( \lambda _{{2}}-\phi _{{11}} \right) \Big ( \left( \lambda _{{2}}-\phi _{{11}} \right) \Upsilon _{{2}}+\phi _{{12}}\Upsilon _{{1}} \Big ) \big ( \phi _{{12}}\Upsilon _{{1}}- \left( 1+ \phi _{{11}} \right) \Upsilon _{{2}} \big ) }{{\phi _{{12}}}^{2} \left( \lambda _{{2}}+1 \right) ^{3}}},\\ h_{5}=&{\frac{ 1 }{{\phi _{{12}}}^{2} \left( \lambda _{{2}}+1 \right) ^{2} \left( \lambda _{{2}}-1 \right) }}\Big [2\,\Big ( {\phi _{{12}}}^{3}\phi _{{23}}+ \big ( \left( \phi _{{13}}-\phi _{{24}} \right) \phi _{{11}}+ ( \frac{1}{2}\,\phi _{{24}}-\phi _{{13}} ) \lambda _{{2}}-\frac{1}{2}\,\phi _{{24}} \big ) {\phi _{{12}}}^{2}\\&-\frac{1}{2}\,\phi _{{14}}\phi _{{12}} \left( \lambda _{{2}}-\phi _{{11}} \right) \left( \lambda _{{2}}-2\,\phi _{{11}}-1 \right) +\phi _{{15}} \left( 1+\phi _{{11}} \right) \left( \lambda _{{2}}-\phi _{{11}} \right) ^{2} \Big ) \big ( {\phi _{{12}}}^{3}\phi _{{23}}+ ( \phi _{{13}}\\ {}&-\phi _{{24}} ) \left( 1+\phi _{{11}} \right) {\phi _{{12}}}^{2}-\phi _{{14}}\phi _{{12}} \left( 1+\phi _{{11}} \right) ^{2}+\phi _{{15}} \left( 1+\phi _{{11}} \right) ^{3} \big ) \Big ]. \end{aligned} \end{aligned}$$

For the map (13) to exhibit a period-doubling bifurcation, the following discriminatory quantities must be non-zero:

$$\begin{aligned} \begin{aligned}&\Lambda _{1}=\left. \left( \frac{\partial ^{2} f}{\partial X_{n} \partial r^{*}}+\frac{1}{2} \frac{\partial f}{\partial r^{*}} \frac{\partial ^{2} f}{\partial X_{n}^{2}}\right) \right| _{(0,0)}, \\&\Lambda _{2}=\left. \left( \frac{1}{6} \frac{\partial ^{3} f}{\partial X_{n}^{3}}+\left( \frac{1}{2} \frac{\partial ^{2} f}{\partial X_{n}^{2}}\right) ^{2}\right) \right| _{(0,0)}. \end{aligned} \end{aligned}$$

After performing calculations, we obtain the following values for these discriminatory quantities:

$$\begin{aligned} \Lambda _{1}=h_{2}+\frac{1}{2}h_{3}, \end{aligned}$$

and

$$\begin{aligned} \Lambda _{2}=h_{5}+h_{1}^{2}. \end{aligned}$$

Using the analysis and theorems in [11,12,13,14,15], we can state the following proposition:

Proposition 3.1

If \(\Lambda _{2} \ne 0\), the map (10) displays a period-doubling bifurcation near \(P_{E_{1}}\) when r changes in a small vicinity of the unique positive equilibrium \(E_{1}\). Moreover, if \(\Lambda _{2}>0\) (resp. \(\Lambda _{2}<0\)), the period-2 points that emerge from \(E_{1}\) are stable (resp. unstable). \(\square \)

4 Numerical simulations

We utilized Matlab software to generate bifurcation diagrams and phase portraits for various parameter values of system (4). Our simulations confirm our theoretical findings and demonstrate unique dynamic behaviors in the system. Specifically, we studied specific cases of system (4) to verify the local asymptotic stability of its positive equilibrium point \(E_{1}\) and observe its period-doubling bifurcation for certain parameter values.

We begin our analysis by examining the parameter region of system (4), where r and \(\alpha \) lie within the sink region shown in Fig. 1. In this region, the positive equilibrium point \(E_{1}\) is asymptotically stable, as confirmed by our simulations presented in Fig. 2a–c.

Next, we consider the case where \(\alpha =0.6\) and the initial value is (1.4, 1.1), and increase the value of r. Specifically, we vary r while keeping \(\alpha \) fixed and observe that when the ordered-pair \((r,\alpha )\) lies exactly on the curve \(r=\frac{4(\alpha -1)}{\left( \alpha ^3-4 \alpha ^2+3 \alpha -2\right) }\textrm{e}^{\frac{1-2 \alpha }{\alpha -1}}\), at \(r\approx 1.852495810\), the equilibrium point \(E_{1}\) loses its stability via a period-doubling bifurcation. Figure 2d–l shows the emergence of a period-2 orbit, followed by period-4, period-8, and so on. As r is further increased, chaotic behavior occurs (see Fig. 2).

The bifurcation diagram and maximum Lyapunov exponent of system (4) with respect to the bifurcating parameter r are shown in Fig. 3. The bifurcation diagram illustrates the various types of behavior exhibited by the system as r is varied. We observe the period-doubling bifurcation and the onset of chaos near \(r\approx 1.852495810\), which is consistent with our theoretical analysis. In addition, the positive value of the maximum Lyapunov exponent indicates that the trajectories of the system diverge exponentially over time, which is a characteristic of chaotic behavior (see Fig. 3).

Fig. 2
figure 2

Phase portraits for various values of r from 1.2 to 2.5

Full size image
Fig. 3
figure 3

Bifurcation diagram and maximum Lyapunov exponent

Full size image

5 Conclusion

In this study, we have investigated the dynamical behaviors of the model (4). The model has two equilibria, \(E_{0}\) and \(E_{1}\), and we have explored their local stability along topological types using the linearization method. Our analysis in Sect. 3.1 has shown that the system undergoes period-doubling bifurcation and chaos near the equilibrium \(E_{1}\) as the parameter r varies in a small neighborhood of \(r\approx 1.852495810\).

We have supported our theoretical findings with numerical simulations, which have demonstrated not only the correctness of our results, but also the complexity of the system’s behavior, such as the emergence of period-2, -4, and -8 orbits.

We find that using the Ricker map, given by \(r X_{n}(e^{1-X_{n}})\), produces more realistic results than logistic growth, given by \(rX_{n}(1-X_{n})\). This is because the Ricker map more accurately captures the behavior of real-world ecological systems, where population growth is limited by factors such as resource availability and predation.

Although we have obtained local stability and bifurcation analysis, the global qualitative behavior of the model (4) is yet to be determined. We will leave it for future work.