Skip to main content
SpringerLink
Log in

Homotopy types of diffeomorphism groups of polar Morse–Bott foliations on lens spaces, 2

  • Published:
Journal of Homotopy and Related Structures Aims and scope Submit manuscript

Abstract

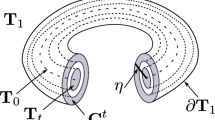
Let \({\mathcal {F}}\) be a Morse–Bott foliation on the solid torus \(T=S^1\times D^2\) into 2-tori parallel to the boundary and one singular central circle. Gluing two copies of T by some diffeomorphism between their boundaries, one gets a lens space \(L_{p,q}\) with a Morse–Bott foliation \({\mathcal {F}}_{p,q}\) obtained from \({\mathcal {F}}\) on each copy of T and thus consisting of two singular circles and parallel 2-tori. In the previous paper Khokliuk and Maksymenko (J Homotopy Relat Struct 18:313–356. https://doi.org/10.1007/s40062-023-00328-z, 2024) there were computed weak homotopy types of the groups \({\mathcal {D}}^{lp}({\mathcal {F}}_{p,q})\) of leaf preserving (i.e. leaving invariant each leaf) diffeomorphisms of such foliations. In the present paper it is shown that the inclusion of these groups into the corresponding group \({\mathcal {D}}^{fol}_{+}({\mathcal {F}}_{p,q})\) of foliated (i.e. sending leaves to leaves) diffeomorphisms which do not interchange singular circles are homotopy equivalences.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. In fact, it will become a right action if we define it by \(\mu (h,f) = f\circ h\). However, it will be convenient to use the terms “left-right” and “right” to refer the sides at which we apply the corresponding diffeomorphisms to \(f\).

  2. Usually an atlas of a manifold \(M\) is a collection of open embeddings \({\mathbb {R}}^{n} \supset U_i \xrightarrow {\psi _i}M\), \(i\in \Lambda \), from open subsets of \({\mathbb {R}}^{n}\) such that \(M= \cup _{i\in \Lambda } \psi _i(U_i)\). However, all the theory of manifolds will not be changed if one extends the notion of an atlas allowing each \(U_i\) to be an open subset of some n-manifold such that the corresponding transition functions are smooth maps.

References

  1. Smale, S.: Diffeomorphisms of the \(2\)-sphere. Proc. Am. Math. Soc. 10, 621–626 (1959). https://doi.org/10.1090/S0002-9939-1959-0112149-8

    Article  MathSciNet  Google Scholar 

  2. Earle, C.J., Eells, J.: A fibre bundle description of Teichmüller theory. J. Differ. Geom. 3, 19–43 (1969)

    Article  Google Scholar 

  3. Earle, C.J., Schatz, A.: Teichmüller theory for surfaces with boundary. J. Differ. Geom. 4, 169–185 (1970). https://doi.org/10.4310/jdg/1214429381

    Article  Google Scholar 

  4. Gramain, A.: Le type d’homotopie du groupe des difféomorphismes d’une surface compacte. Ann. Sci. École Norm. Sup. (4) 6, 53–66 (1973). https://doi.org/10.24033/asens.1242

    Article  MathSciNet  Google Scholar 

  5. Hatcher, A.: A proof of the Smale conjecture, \({\rm Diff}(S^{3})\simeq {\rm O}(4)\). Ann. Math. (2) 117(3), 553–607 (1983). https://doi.org/10.2307/2007035

    Article  MathSciNet  Google Scholar 

  6. Gabai, D.: The Smale conjecture for hyperbolic 3-manifolds: \({\rm Isom}(M^3)\simeq {\rm Diff}(M^3)\). J. Differ. Geom. 58(1), 113–149 (2001)

    Article  MathSciNet  Google Scholar 

  7. Hong, S., Kalliongis, J., McCullough, D., Rubinstein, H.: Diffeomorphisms of Elliptic 3-manifolds. Lecture Notes in Mathematics, vol. 2055, p. 155. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31564-0

  8. Novikov, S.P.: Differentiable sphere bundles. Izv. Akad. Nauk SSSR Ser. Mat. 29, 71–96 (1965)

    MathSciNet  Google Scholar 

  9. Schultz, R.: Improved estimates for the degree of symmetry of certain homotopy spheres. Topology 10, 227–235 (1971). https://doi.org/10.1016/0040-9383(71)90007-3

    Article  MathSciNet  Google Scholar 

  10. Hajduk, B.: On the homotopy type of diffeomorphism groups of homotopy spheres. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 26(12), 1003–10061979 (1978)

    MathSciNet  Google Scholar 

  11. Dwyer, W.G., Szczarba, R.H.: On the homotopy type of diffeomorphism groups. Ill. J. Math. 27(4), 578–596 (1983)

    MathSciNet  Google Scholar 

  12. Kupers, A.: Some finiteness results for groups of automorphisms of manifolds. Geom. Topol. 23(5), 2277–2333 (2019). https://doi.org/10.2140/gt.2019.23.2277

    Article  MathSciNet  Google Scholar 

  13. Berglund, A., Madsen, I.: Rational homotopy theory of automorphisms of manifolds. Acta Math. 224(1), 67–185 (2020). https://doi.org/10.4310/acta.2020.v224.n1.a2

    Article  MathSciNet  Google Scholar 

  14. Rybicki, T.: The identity component of the leaf preserving diffeomorphism group is perfect. Monatsh. Math. 120(3–4), 289–305 (1995). https://doi.org/10.1007/BF01294862

    Article  MathSciNet  Google Scholar 

  15. Tsuboi, T.: On the group of foliation preserving diffeomorphisms. In: Foliations 2005, pp. 411–430. World Sci. Publ., Hackensack (2006). https://doi.org/10.1142/9789812772640_0023

  16. Herman, M.-R.: Simplicité du groupe des difféomorphismes de classe \(C^{\infty }\), isotopes à l’identité, du tore de dimension \(n\). C. R. Acad. Sci. Paris Sér. A-B 273, 232–234 (1971)

  17. Thurston, W.: Foliations and groups of diffeomorphisms. Bull. Am. Math. Soc. 80, 304–307 (1974)

    Article  MathSciNet  Google Scholar 

  18. Mather, J.N.: The vanishing of the homology of certain groups of homeomorphisms. Topology 10, 297–298 (1971). https://doi.org/10.1016/0040-9383(71)90022-X

    Article  MathSciNet  Google Scholar 

  19. Mather, J.N.: Simplicity of certain groups of diffeomorphisms. Bull. Am. Math. Soc. 80, 271–273 (1974)

    Article  MathSciNet  Google Scholar 

  20. Epstein, D.B.A.: The simplicity of certain groups of homeomorphisms. Compos. Math. 22, 165–173 (1970)

    MathSciNet  Google Scholar 

  21. Fukui, K.: Homologies of the group \({\rm Diff}^{\infty }({ R}^{n},\,0)\) and its subgroups. J. Math. Kyoto Univ. 20(3), 475–487 (1980). https://doi.org/10.1215/kjm/1250522211

    Article  MathSciNet  Google Scholar 

  22. Rybicki, T.: On the group of diffeomorphisms preserving a submanifold. Demonstr. Math. 31(1), 103–110 (1998)

    MathSciNet  Google Scholar 

  23. Maksymenko, S.: Local inverses of shift maps along orbits of flows. Osaka J. Math. 48(2), 415–455 (2011). arXiv:0806.1502

  24. Lech, J., Michalik, I.: On the structure of the homeomorphism and diffeomorphism groups fixing a point. Publ. Math. Debr. 83(3), 435–447 (2013). https://doi.org/10.5486/PMD.2013.5551

    Article  MathSciNet  Google Scholar 

  25. Fukui, K., Ushiki, S.: On the homotopy type of \(F{\rm Diff} (S^{3},\)\({{\cal{F} }}_{R})\). J. Math. Kyoto Univ. 15, 201–210 (1975). https://doi.org/10.1215/kjm/1250523125

    Article  MathSciNet  Google Scholar 

  26. Fukui, K.: On the homotopy type of some subgroups of \( {\rm Diff}(M^{3})\). Japan. J. Math. (N.S.) 2(2), 249–267 (1976). https://doi.org/10.4099/math1924.2.249

  27. Mather, J.N.: Stability of \(C^{\infty }\) mappings. I. The division theorem. Ann. Math. (2) 87, 89–104 (1968)

  28. Sergeraert, F.: Un théorème de fonctions implicites sur certains espaces de Fréchet et quelques applications. Ann. Sci. École Norm. Sup. 4(5), 599–660 (1972)

    Article  Google Scholar 

  29. Mond, D., Nuño-Ballesteros, J.J.: Singularities of mappings—the local behaviour of smooth and complex analytic mappings. Grundlehren der mathematischen Wissenschaften, vol. 357, p. 567. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-34440-5

  30. Maksymenko, S.: Smooth shifts along trajectories of flows. Topol. Appl. 130(2), 183–204 (2003). https://doi.org/10.1016/S0166-8641(02)00363-2

    Article  MathSciNet  Google Scholar 

  31. Maksymenko, S.: Homotopy types of stabilizers and orbits of Morse functions on surfaces. Ann. Glob. Anal. Geom. 29(3), 241–285 (2006). https://doi.org/10.1007/s10455-005-9012-6

    Article  MathSciNet  Google Scholar 

  32. Maksymenko, S.: Homotopy types of right stabilizers and orbits of smooth functions functions on surfaces. Ukr. Math. J. 64(9), 1186–1203 (2012). https://doi.org/10.1007/s11253-013-0721-x. arXiv:1205.4196

  33. Maksymenko, S.: Deformations of functions on surfaces by isotopic to the identity diffeomorphisms. Topol. Appl. 282, 107312–48 (2020). https://doi.org/10.1016/j.topol.2020.107312

    Article  MathSciNet  Google Scholar 

  34. Leygonie, J., Beers, D.: Fiber of persistent homology on Morse functions. J. Appl. Comput. Topol. 7(1), 89–102 (2023). https://doi.org/10.1007/s41468-022-00100-x

    Article  MathSciNet  Google Scholar 

  35. Khokhliuk, O., Maksymenko, S.: Diffeomorphisms preserving Morse–Bott functions. Indag. Math. (N.S.) 31(2), 185–203 (2020). https://doi.org/10.1016/j.indag.2019.12.004

    Article  MathSciNet  Google Scholar 

  36. Khokhliuk, O., Maksymenko, S.: Smooth approximations and their applications to homotopy types. Proc. Int. Geom. Cent. 13(2), 68–108 (2020). https://doi.org/10.15673/tmgc.v13i2.1781

  37. Khokhliuk, O., Maksymenko, S.: Foliated and compactly supported isotopies of regular neighborhoods (2022). arXiv:2208.05876

  38. Khokhliuk, O., Maksymenko, S.: Homotopy types of diffeomorphism groups of polar Morse-Bott foliations on lens spaces, 1. J. Homotopy Relat. Struct. 18, 313–356 (2023). https://doi.org/10.1007/s40062-023-00328-z

    Article  MathSciNet  Google Scholar 

  39. Ivanov, N.: Homotopy of spaces of diffeomorphisms of some three-dimensional manifolds. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), Studies in topology, IV, vol. 122, pp. 72–103164165 (1982)

  40. Maksymenko, S.: Stabilizers and orbits of smooth functions. Bull. Sci. Math. 130(4), 279–311 (2006). https://doi.org/10.1016/j.bulsci.2005.11.001

    Article  MathSciNet  Google Scholar 

  41. Reidemeister, K.: Homotopieringe und Linsenräume. Abh. Math. Sem. Univ. Hamburg 11(1), 102–109 (1935). https://doi.org/10.1007/BF02940717

    Article  MathSciNet  Google Scholar 

  42. Brody, E.J.: The topological classification of the lens spaces. Ann. Math. 2(71), 163–184 (1960). https://doi.org/10.2307/1969884

    Article  MathSciNet  Google Scholar 

  43. Bonahon, F.: Difféotopies des espaces lenticulaires. Topology 22(3), 305–314 (1983). https://doi.org/10.1016/0040-9383(83)90016-2

    Article  MathSciNet  Google Scholar 

  44. Gadgil, S.: Cobordisms and Reidemeister torsions of homotopy lens spaces. Geom. Topol. 5, 109–125 (2001). https://doi.org/10.2140/gt.2001.5.109

    Article  MathSciNet  Google Scholar 

  45. Whitney, H.: Differentiable even functions. Duke Math. J. 10, 159–160 (1943). https://doi.org/10.1215/S0012-7094-43-01015-4

    Article  MathSciNet  Google Scholar 

  46. Dubovski, B.: Proof that smooth positive degree \(m\) homogeneous function is polynomial of degree \(m\) and \(m\) is a positive integer (2017). https://math.stackexchange.com/q/2303795

  47. Wajnryb, B.: Mapping class group of a handlebody. Fund. Math. 158(3), 195–228 (1998). https://doi.org/10.4064/fm-158-3-195-228

    Article  MathSciNet  Google Scholar 

  48. Kalliongis, J., Miller, A.: Geometric group actions on lens spaces. Kyungpook Math. J. 42(2), 313–344 (2002)

    MathSciNet  Google Scholar 

  49. Balmer, R., Kleiner, B.: Ricci flow and contractibility of spaces of metrics (2019)

  50. Hatcher, A.: On the diffeomorphism group of \(S^{1}\times S^{2}\). Proc. Am. Math. Soc. 83(2), 427–430 (1981). https://doi.org/10.2307/2043543

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author is sincerely grateful to anonymous Referee for very useful remarks and suggestions which allowed to improve the contents of the paper and exposition.

Author information

Authors and Affiliations

  1. Algebra and Topology Department, Institute of Mathematics, NAS of Ukraine, Tereshchenkivska Str., 3, Kyiv, 01024, Ukraine

    Sergiy Maksymenko

Authors
  1. Sergiy Maksymenko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergiy Maksymenko.

Additional information

Communicated by Benson Farb.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maksymenko, S. Homotopy types of diffeomorphism groups of polar Morse–Bott foliations on lens spaces, 2. J. Homotopy Relat. Struct. 19, 239–273 (2024). https://doi.org/10.1007/s40062-024-00346-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40062-024-00346-5

Keywords

Mathematics Subject Classification

Search

Navigation