1 Introduction

Understanding nature with a minimal number of guiding principles is one of the goals of science. Among innumerable theories in science, quantum electrodynamics [1] has achieved the most accurately tested physics theory constructed ever in human history. The eight-digit agreements between the theory and experiment regarding the anomalous magnetic dipole moment of the electron first computed by Schwinger [2] and the Rydberg constant (see Aoyama et al. [3] for a review) rely only on a single parameter called the fine-structure constant \(\alpha\). Such an unprecedented success of quantum field theory was achieved due to the development of a rigorous quantitative approximation formalism called perturbation theory, which expands a physical measurable in a power series in a small perturbative parameter \(\alpha ={\text{e}}^2/(4\pi \varepsilon _0 \hbar c)\). Here, the coupling constant e is the elementary electric charge representing the strength of the electron–photon interaction, \(\varepsilon _0\) is the vacuum permittivity, \(\hbar\) is the reduced Planck constant, and c is the speed of light in vacuum.

In the perturbative expansion of a physical amplitude involving relativistic particles, an external state, which is directly observable, is on its own mass shell in that the squared four-momentum \(p^2\) satisfies \(p^2=(E/c)^2-{\varvec{p}}^2=m^2c^2\), where E and \({\varvec{p}}\) are the energy and three-momentum of the particle of rest mass m. In that amplitude, a virtual state of a field may also arise as the propagator. Here, a virtual state is off its mass shell: \(p^2=(E/c)^2-{\varvec{p}}^2\ne m^2c^2\). The wave propagation of the virtual state of a field is described by the Feynman propagator [4] that is Green’s function [5] of the equation of motion for the field. The Feynman propagator can be compactly expressed as a Fourier transform in the momentum space. This is a linear combination of free-field waves with the multiplicative factor \(i/(d+i\varepsilon )\), where \(d=p^2-m^2c^2\). Note that we have suppressed the numerator factor that depends on the spin of the particle. Here, \(+i\varepsilon\) is a pure imaginary number with an infinitesimally small positive number \(\varepsilon \rightarrow 0^+\). This additional piece in the propagator denominator respects the causality boundary condition of Green’s function which is required by Huygens’ principle of propagating wave for a relativistic particle. A formal description of the propagator theory can be found, for example, in chapter 6 of Bjorken and Drell [6].

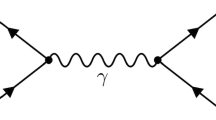
The Feynman diagram is a convenient representation for the perturbative series of an amplitude involving quantum fields. As the order of the perturbative parameter increases, the number of vertices and the number of propagators increase simultaneously. Each vertex has a suppression factor of the coupling such as e. Keeping the external particles unchanged, this leads to a new topological Feynman diagram called the loop. As an example, we consider the magnetic dipole moment of the electron. At leading order in \(\alpha\), the Dirac equation [7, 8], which is the relativistic equation of motion for the electron, gives the gyromagnetic ratio g of the electron exact \(g=2\). (See, for example, p 13 of Bjorken and Drell [6].) The anomalous magnetic moment \(a_e=(g-2)/2\) represents the relative shift from the exact 2 that must come from the perturbative corrections. At the next-to-leading order in \(\alpha\), the Feynman diagram acquires a triangular loop diagram being called the vertex correction as shown in Fig. 1.

Fig. 1
figure 1

The Feynman diagram of the triangular loop involving the quantum electrodynamics vertex correction. Here, the bold line and the wavy line represent an electron and a photon, respectively

Full size image

This is the leading contribution to \(a_e=(g-2)/2\). This amplitude involves the loop integral with the loop momentum \(k^{\mu}\) whose every component is free to vary from \(-\infty\) to \(\infty\). In that amplitude, there are three propagators of the form \(1/(a_1 a_2 a_3)\), where \(a_1\) and \(a_2\) are the propagator denominators for the electron adjacent to the electron-photon vertex and \(a_3\) is the denominator of the photon propagator that is exchanged by the initial and the final electron states. Readers are referred to chapter 17 of Schwartz [9] or chapter 6 of Peskin and Schroeder [10] for further reading.

In fact, any loop integral can be at first evaluated by integrating over the energy component \(k^0\) of the loop momentum \(k^{\mu}\) by making use of the calculus of residues that derives from the Cauchy integral theorem for an analytic function [11,12,13]. Then we are left with an integral over the three-dimensional Euclidean space. Although the integral must be a Lorentz-covariant quantity, in principle, the Euclidean integral is naturally expressed in terms of non-covariant terms, unfortunately. Furthermore, as the number of denominator factors increases, the number of terms contributing to the residue piles up formidably. Thus, this method is not practically useful. A convenient way to avoid such a messy computation is the Feynman parametrization, which combines all of the denominator factors emerging in the integrand of a loop integral into a single power. An explicit form can be found, for example, in equation (6.42) on p 190 of Peskin and Schroeder [10]. The method is an intricate application of the partial-fraction decomposition for a rational function in combination with integration and differentiation techniques. If the Schwinger parametrization [14] is applied together, then the derivation of the Feynman parametrization becomes particularly straightforward.

In this paper, we focus on the derivation of the Schwinger parametrization and the Feynman parametrization rather than applying the parametrization to compute loop integrals. The fundamental form of the Schwinger parametrization is nothing but the Laplace transform of the Heaviside step function that can be analytically continued to the Fourier-transform representation. The Fourier-transform representation is more effective in physics because the real part of a propagator denominator can hit 0, which is not allowed in the Laplace transform representation. The more general form of the Schwinger parametrization can be derived by performing multiple partial derivatives and utilizing the analyticity of the gamma function. An elementary derivation of the Feynman parametrization involves only the algebra of partial-fraction decomposition and elementary calculus with an additional application of the Dirac delta function for changing variables. If we have a closer look into the derivation in terms of the Schwinger parametrization, then the derivation of the parametrization involves an extensive use of the analytic properties of complex functions. In addition, the combinatorial factor arising in the integration of the Feynman parameters is an elementary integral embedded in the time-ordered product of the Dyson series in the time-dependent perturbation theory. Furthermore, the multivariate beta function can be derived as a byproduct of the parametrization.

The formulation is indeed closely related to the analytic continuation of quantum-mechanical amplitude. Thus, the target reader of this paper is mainly upper-level physics major undergraduate students who have studied quantum mechanics. Graduate students of particle-physics major may have a nice chance to investigate in detail about the derivation because the Feynman parametrization is usually introduced in the appendix of a quantum field theory textbook briefly without a detailed proof. We believe that the derivation presented in this paper is pedagogically useful in that students can train themselves with various mathematical tools widely employed in physics in a single problem.

This paper is organized as follows. In Sect. 2, we investigate the analytic structure of the Feynman propagator and the generic form of loop integrals. In Sect. 3, we review the analytic properties of the Schwinger parametrization that stems from the Laplace transform of the Heaviside step function and derive the most general form of the Schwinger parametrization. Section 4 contains the derivation of the Feynman parametrization with partial-fraction decomposition and the derivation of its general form applicable to parametrizing denominators with arbitrary powers. A set of elementary applications of the Schwinger parametrization and the Feynman parametrization is illustrated in Sect. 5. The applications include a Feynman-parameter integral involving combinatorial factor embedded in the time-ordering operation of the time-dependent perturbation theory and a derivation of the multivariate beta function. The conclusion follows in Sect. 6. An explicit evaluation of the contour integral for the Feynman propagator is given in Appendix A to demonstrate the causality boundary condition for Green’s function that corresponds to the relativistic propagator. The calculation detail of the derivation of the general form of the Feynman parameterization from the Schwinger parametrization is provided in Appendix B.

2 Analytic structure of loop integrals

In this section, we review the analytic properties of the propagator–denominator factors appearing in a loop integral that emerges in the perturbative series of an amplitude in relativistic quantum field theory. Because the propagator–denominator factor is independent of the spin, we simplify our review by considering a scalar field \(\phi (x)\) representing a spin-0 particle of rest mass m.

2.1 Feynman propagator

The relativistic equation of motion for the scalar field \(\phi (x)\) of rest mass m is the Klein–Gordon equation [see equation (8) of Gordon [15]]:

$$\begin{aligned} \left[ -\partial ^2-m^2\right] \phi (x)=0, \end{aligned}$$
(1)

where we have taken the natural unit system in which the speed of light \(c=1\) and the reduced Planck constant \(\hbar =1\). Here, the operator \(\partial ^2\) is defined by

$$\begin{aligned} \partial ^2\equiv \frac{\partial ^2}{\partial (x^0)^2} -\frac{\partial ^2}{\partial (x^1)^2} -\frac{\partial ^2}{\partial (x^2)^2} -\frac{\partial ^2}{\partial (x^3)^2}. \end{aligned}$$
(2)

Note that \(x^{\mu} =(x^0,x^1,x^2,x^3)=( t,{\varvec{x}})\) is the space-time coordinate defined in the Minkowski space. The general solution \(\phi _{0}(x)\) for Eq. (1) is given by

$$\begin{aligned} \phi _{0}(x)=\kappa _1 {\text{e}}^{i p\cdot x}+\kappa _2 {\text{e}}^{-i p\cdot x}, \end{aligned}$$

where p and x are the four-momentum and the space-time coordinate of the field, respectively, and \(\kappa _i\) are arbitrary constants that are determined by initial conditions. If there is an interaction of \(\phi (x)\) with a current J(x), then the equation is not given as a homogeneous equation like Eq. (1) but given as a nonhomogeneous equation

$$\begin{aligned} \left[ -\partial ^2-m^2\right] \phi (x)=J(x). \end{aligned}$$
(3)

In that case, a particular solution of \(\phi _{\text{P}}(x)\) can be obtained by convolving with Green’s function \(\Delta _{\text{F}}(x-y)\) as

$$\begin{aligned} \phi _{\text{P}}(x) = \int {\text{d}}^{4}y\, \Delta _{\text{F}}(x-y)\,J(y), \end{aligned}$$
(4)

where Green’s function \(\Delta _{\text{F}}(x-y)\) satisfies the following equation

$$\begin{aligned} \left[ \partial ^2+m^2\right] \Delta _{\text{F}}(x-y)=-\delta ^{(4)}(x-y). \end{aligned}$$
(5)

Here, \(\delta ^{(4)}(x-y)\) is the four-dimensional Dirac delta function. Such a partial differential equation for Green’s function can be solved conveniently by performing the Fourier transform [16,17,18] into the momentum space. The Fourier-transform representations of \(\phi (x)\) and \(\delta ^{(4)}(x-y)\) are expanded in linear combinations of the free-particle wavefunction \(\phi _p(x)\equiv {\text{e}}^{-ip\cdot x}\) in the configuration space, where \(p^{\mu} =(p^0,{\varvec{p}})\) is the four-momentum and \(p\cdot x=p^0x^0-{\varvec{p}}\cdot {\varvec{x}}\),

$$\begin{aligned}{} & {} \phi (x)=\int \frac{{\text{d}}^4p}{(2\pi )^4}{\tilde{\phi }}(p){\text{e}}^{-ip\cdot x }, \\{} & {} \delta ^{(4)}(x-y)=\int \frac{{\text{d}}^4p}{(2\pi )^4}{\text{e}}^{-ip\cdot (x-y)}. \end{aligned}$$
(6)

Here, each of the four components of the momentum \(p^{\mu}\) is integrated over the interval \((-\infty ,\infty )\) and the oscillating factor \({\text{e}}^{-ip\cdot (x-y)}= \phi _p(x)\phi _p^\star (y)\) behaves as the projection operator that projects out the free-particle state of three-momentum \({\varvec{p}}\). \({\tilde{\phi }}(p)\) is the momentum-space wavefunction.

The Feynman propagator \(i\Delta _{\text{F}}(x-y)\) is nothing but Green’s function up to a complex phase as

$$\begin{aligned} i\Delta _{\text{F}}(x-y)\equiv \int \frac{{\text{d}}^4p}{(2\pi )^4}\,i{\tilde{\Delta }}_{\text{F}}(p) {\text{e}}^{-ip\cdot (x-y)}, \end{aligned}$$
(7)

where \(p^{\mu}\) is the four-momentum of the propagating scalar field and the integration for every component is over \((-\infty ,\infty )\). Here, the factor \(i{\tilde{\Delta }}_{\text{F}}(p)\) is called the momentum-space representation of the propagator with four-momentum \(p^{\mu}\) that can be obtained by substituting the expression (7) for that in Eq. (5) as

$$\begin{aligned} i{\tilde{\Delta }}_{\text{F}}(p)=\frac{i}{p^2-m^2+i\varepsilon }. \end{aligned}$$
(8)

Here, \(\varepsilon\) is an infinitesimally small positive number that is introduced to avoid the singularity at \(p^2=m^2\). The choice of the sign \(+i\varepsilon\) corresponds to the causality boundary condition for Green’s function that can be shown by carrying out the integration of Green’s function over \(p^{0}\) as

$$\begin{aligned} i\Delta _{\text{F}}(x-y)=\, & {} \theta (x^{0}-y^{0})\int \frac{{\text{d}}^{3}{\varvec{p}} }{(2\pi )^3 2E_{{\varvec{p}}}}{\text{e}}^{-ip\cdot (x-y)} \\{} & {} +\theta (y^{0}-x^{0})\int \frac{{\text{d}}^{3}{\varvec{p}} }{(2\pi )^3 2E_{{\varvec{p}}}}{\text{e}}^{-ip\cdot (y-x)}, \end{aligned}$$
(9)

where \(p^{0}=E_{{\varvec{p}}}=\sqrt{{\varvec{p}}^2+m^2}>0\). The derivation of the result in Eq. (9) is presented in Appendix A. Such a use of \(+i\varepsilon\) to impose a causality boundary condition also can be found in the integral representation of the Heaviside step function, which is well discussed in reference [19]. More detailed explanations on the expression in Eqs. (7) and (8) can be found, for example, on pp 186–188 of Bjorken and Drell [6] and in equation (7.69) of Schwartz [9].

The Fourier-transform representation of the Feynman propagator \(i\Delta _{\text{F}}(x-y)\) in the position space given in Eq. (7) represents the propagation of the scalar field from a space-time coordinate \(y^{\mu}\) to \(x^{\mu}\) expanded in a linear combination of free-particle waves \({\text{e}}^{-ip\cdot (x-y)}\).

The expression in Eq. (7) is the consequence of the Wick theorem [20] for quick rewriting the time-ordered field operator product in perturbation theory that is explained well in Box 7.3 on p 102 of Schwartz [9]. The Wick theorem respects the causality boundary condition of Green’s function which is the fundamental background of the two equivalent formalisms of describing the time evolution of the quantum system: the Feynman propagator [4, 21] and the Dyson series expansion for the S matrix [22, 23].

Under the Lorenz condition \(\partial _{\mu} A^{\mu} =0\), Maxwell’s equation \(\partial _{\mu }F^{\mu \nu }=0\) in free space collapses to \(\partial _{\mu} \partial ^{\mu} A^{\nu} =0\). Hence, every component of the four-vector potential \(A^{\nu}\) satisfies the Klein–Gordon equation (1) in the massless limit, \(m\rightarrow 0\). As a result, the retarded and advanced Green’s functions of classical electrodynamics satisfying the Lorenz gage condition are closely related to the positive-energy contribution \([\theta (x^{0}-y^{0})\) term] and the negative-energy contribution \([\theta (y^{0}-x^{0})\) term], respectively, in the massless limit of the Feynman propagator in Eq. (7), except that the pole structure in Eq. (8) should be modified with the standard prescription in classical electrodynamics as

$$\begin{aligned}{} & {} i\Delta _{\text{retarded}}(x-y) \\{} & {} \quad \equiv \int \frac{{\text{d}}^4p}{(2\pi )^4}\,\frac{i}{(p^{0}+ i\varepsilon )^2-{\varvec{p}}^2} {\text{e}}^{-ip\cdot (x-y)}, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} i\Delta _{\text{advanced}}(x-y) \\{} & {} \quad \equiv \int \frac{{\text{d}}^4p}{(2\pi )^4}\,\frac{i}{(p^{0}- i\varepsilon )^2-{\varvec{p}}^2} {\text{e}}^{-ip\cdot (x-y)}. \end{aligned}$$
(11)

Readers are referred to Section 12.11 of Jackson [24] for more details including the contour shown in Figure 12.7 of that reference.

2.2 Loop integrals

The perturbative expansion of the momentum-space representation of the amplitude for a process involving N external particles with four-momenta \(p_1,\ldots ,p_N\) is expressed as a series in powers of a perturbative coupling. In quantum electrodynamics, the fine-structure constant \(\alpha = {\text{e}}^2/(4\pi )\), is the perturbative expansion parameter. At the leading order in \(\alpha\), the scattering amplitude has propagators whose momenta are completely fixed in linear combinations of the four-momenta for the external particles. At the next-to-leading order in \(\alpha\), the corresponding Feynman diagram acquires a loop whose loop momentum \(k^{\mu}\) ranges from \(-\infty\) to \(\infty\) for any of the four components. Suppose that the loop involves n \((\le N)\) propagators. As is given in ’t Hooft and Veltman [25], the next-to-leading-order amplitude contains a loop integral as a multiplicative factor whose generic form is

$$\begin{aligned} I=\int \frac{{\text{d}}^4k}{(2\pi )^4} \frac{1}{ (d_1+i\varepsilon )^{\alpha _1} \cdots (d_n+i\varepsilon )^{\alpha _n}}. \end{aligned}$$
(12)

Here, \(\alpha _i=1\) for an ordinary case but we may allow \(\alpha _i\) to be any positive integer since such a power may arise in a specific effective field theory. The integral (12) is over the loop momentum \(k^{\mu}\) whose four components are integrated over \((-\infty ,\infty )\) independently. In fact, we should also consider the numerator that contains the loop momentum. However, we have not specified it explicitly in Eq. (12). One can employ the tensor-integral reduction to remove such a factor in the numerator. The standard method of tensor-integral reduction is the Passarino–Veltman reduction given in Passarino and Veltman [26]. An elementary treatment of the tensor-integral reduction can be found in Ee et al. [27].

Fig. 2
figure 2

A Feynman diagram of a loop involving n propagators corresponding to the integral in Eq. (12). Here, the bold line and the wavy line represent a fermion of momentum \(q_i\) and a photon of momentum \(p_i\), respectively

Full size image

There are n vertices and n propagators that are described by the loop integral in Eq. (12). We employ the convention that any one of the external legs has the momentum coming into a vertex as is shown in Fig. 2. The energy–momentum conservation requires that the sum of the external momenta coming into the loop must be the same as the sum of the external momenta going out of the loop. Then, the sum of all of the external momenta always vanishes:

$$\begin{aligned} p_1+p_2+\cdots +p_n=0. \end{aligned}$$
(13)

The first propagator has the momentum \(k+p_1\), where k is the loop momentum and \(p_1\) is the momentum of the external particle that couples to the first vertex. The second propagator carries the momentum \(k+p_1+p_2\), where \(p_2\) is the momentum of the external particle that couples to the second vertex. In this manner, the ith propagator has the momentum \(k+p_1+\cdots +p_{i}\). As a result, the real part \(d_i\) of the denominator \(d_i+i\varepsilon\) of the ith Feynman propagator of mass \(m_i\) in Eq. (12) can be defined as

$$\begin{aligned} d_i=\, & {} q_i^2-m_i^2,\qquad \forall i\in \{1,2,\ldots ,n\}, \\ q_1=\, & {} k+p_1, \\ q_2=\, & {} k+p_1+p_2, \\&\vdots& \\ q_{n-1}=\, & {} k+p_1+\cdots +p_{n-1}, \\ q_n=\, & {} k+p_1+\cdots +p_{n-1}+p_n=k. \end{aligned}$$
(14)

Substituting the momenta in Eq. (14) into the loop integral (12), we find that

$$\begin{aligned} I = \int \frac{{\text{d}}^4k}{(2\pi )^4} \frac{1}{ [ (k+p_1)^2-m_1^2+i\varepsilon ]^{\alpha _1} \cdots [ k^2-m_n^2+i\varepsilon ]^{\alpha _n} }. \end{aligned}$$
(15)

The \(k^0\) integral can be evaluated by making use of the calculus of residues. Then the remaining integral over \({\varvec{k}}\) is defined in the three-dimensional Euclidean space. Evidently in Eq. (15), the integral must be a Lorentz-covariant quantity. However, the Euclidean integral is naturally expressed in terms of non-covariant terms and the number of terms contributing to the residue piles up formidably as the number of denominator factors increases. Thus, this method is not practically useful. The parametrizations of Schwinger and of Feynman were developed to combine the propagator–denominator factors into a single power and allow one to compute the four-dimensional loop integral in a convenient way. This approach introduces additional multiple integral over a set of new parameters though. Particle-physics major graduate students are referred to three books [28,29,30] by Smirnov that contain comprehensive guides to advanced loop-integral techniques.

3 Schwinger parameterization

In this section, we present a kind derivation of the Schwinger parameterization. We first identify that the Schwinger parametrization for the Feynman propagator of a scalar field is equivalent to the Laplace transform [31, 32] of the Heaviside step function. By investigating the analytic properties of the transform, we obtain stringent conditions for the applicability particularly involved with \(+i\varepsilon\) term in the propagator denominator and derive the Fourier-transform version of the parametrization. After that, we derive the most general form of the Schwinger parametrization applicable to the parametrization involving multiple denominators with arbitrary positive powers.

3.1 Representations of the unity

We begin with two integral representations of the unity

$$\begin{aligned} 1= & {} \int _0^\infty {\text{d}}s\, {\text{e}}^{-s}, \\ 1= & {} \int _0^\infty {\text{d}}z\,\delta (z-z_0),\quad z_0>0, \end{aligned}$$
(16)

where the former representation is in terms of a convergent definite integral of an exponential function and the latter is expressed as an integral of the Dirac delta function [33]. As a distribution [34], the Dirac delta function \(\delta (x)\) is defined only through integration:

$$\begin{aligned} \int _{-\infty }^\infty {\text{d}}x\,\delta (x)f(x)=f(0), \end{aligned}$$
(17)

for any continuous integrable function f(x). According to Eq. (17), \(\delta (x)\) must vanish except at \(x=0\). Apparently, \(\delta (x)\) does have a singularity and discontinuity at \(x=0\). We have restricted the integration limits for the Dirac delta function in Eq. (16) that are identical to those of the first integral to make the two relations consistent with each other. Thus, \(z_0\) in the second line of Eq. (16) must be a positive number. Multiplication of unities involving the Dirac delta function is quite useful in changing variables. Pedagogical examples of applying the Dirac delta function to purely algebraic computations can be found in Ee et al. [35] for an alternative proof of the Cramer’s rule to find the inverse matrix and in Kim et al. for an algebraic derivation of the Jacobian for a multi-variable integral [36].

3.2 Schwinger parametrization of Feynman propagator

If we introduce a positive dimensionless number a as an auxiliary scaling parameter to the integrand, then the first identity in Eq. (16) acquires an additional degree of freedom. The number a can be extended to any complex number provided that the real part \({\mathfrak{Re}}[a]\) is positive to guarantee the convergence:

$$\begin{aligned} \frac{1}{a}=\int _0^\infty {\text{d}}s\, {\text{e}}^{-as },\quad {\mathfrak{Re}}[a]>0. \end{aligned}$$
(18)

Apparently, the expression in Eq. (18) has an intrinsic singularity at \(a=0\). This identity can also be understood as the bilateral Laplace transform [31, 32] of the Heaviside step function \(\theta (t)\), which is defined by

$$\begin{aligned} \theta (t)= \left\{ \begin{array}{ll} 0,&{}\quad \text{for } t<0,\\ 1,&{}\quad \text{for } t>0. \end{array}\right. \end{aligned}$$
(19)

While the parametrization in Eq. (18) is convenient for any complex number with positive real part, it is not suitable for parametrizing the momentum-space representation for the Feynman propagator:

$$\begin{aligned} i{\tilde{\Delta }}_{\text{F}}(p)= \frac{i}{p^2-m^2+i\varepsilon },\quad \varepsilon \rightarrow 0^+, \end{aligned}$$
(20)

where p and m are the four-momentum and mass of the propagating field. Here, we have suppressed the numerator factor that depends on the spin of the corresponding particle. The \(\varepsilon\) is an infinitesimal positive number and \(p^2-m^2\) is real. The condition

$$\begin{aligned} {\mathfrak{Re}}[p^2-m^2+i\varepsilon ]>0 \end{aligned}$$

required in Eq. (18) is not guaranteed because the sign of the real part \(p^2-m^2\) can vary depending on the explicit values for the four-momentum components. Only the sign of the imaginary part is positive definite.

Julian Schwinger generalized the integral (18) to reparametrize the Feynman propagator in Eq. (20) in equation (2.24) of Schwinger [14] as

$$\begin{aligned} \frac{i}{a}=\int _0^\infty {\text{d}}s\,{\text{e}}^{ias},\quad {\mathfrak{Im}}[a]>0. \end{aligned}$$
(21)

This corresponds to the Fourier transform [17, 18] of the Heaviside step function that can be derived from the bilateral Laplace transform (18) by replacing the parameter a with \(-ia\). The requirement of the convergence \({\mathfrak{Re}}[a]>0\) in Eq. (18) is correspondingly modified as \({\mathfrak{Im}}[a]>0\) in the Fourier-transform version in Eq. (21). We call the integration variable s a Schwinger parameter. The relation (21) is applicable to the Feynman propagator in Eq. (20) because

$$\begin{aligned} {\mathfrak{Im}}[a]={\mathfrak{Im}}[p^2-m^2+i\varepsilon ]=\varepsilon >0 \end{aligned}$$

regardless of the value for the real part \(p^2-m^2\). Advanced reviews on the Schwinger parametrization that cover a matrix or a differential operator \({\fancyscript{O}}\) can be found, for example, in Peres [37], González and Schmidt [38], or [39].

3.3 Parametrization of a denominator with exponent α ≥ 1

In the previous section, we considered the parametrization of a single power denominator. In general, the power of a denominator may be given as a positive real number in the parametrization. Let us first consider the case in which the power \(\alpha\) of a denominator factor a is a positive integer. In that case, the parametrization can be derived from the expression in Eq. (18) by taking multiple partial derivatives on both sides of the equation:

$$\begin{aligned} \frac{1}{a^\alpha }= & {} \frac{1}{(\alpha -1)!}\left( -\frac{\partial }{\partial a}\right) ^{\alpha -1} \frac{1}{a} \\= & {} \frac{1}{(\alpha -1)!}\int _0^\infty {\text{d}}s\, s^{\alpha -1} {\text{e}}^{-as },\quad {\mathfrak{Re}}[a]>0. \end{aligned}$$
(22)

The parametrization in Eq. (22) can be transformed into Euler’s definition of a gamma function by multiplying \(a^\alpha (\alpha -1)!\) to both sides of the equation and changing variables \(as\rightarrow t\) in the integral as

$$\begin{aligned} (\alpha -1)!=\Gamma [\alpha ]\equiv \int _{0}^{\infty }{\text{d}}t\,t^{\alpha -1}{\text{e}}^{-t}. \end{aligned}$$
(23)

Euler’s definition of the gamma function in Eq. (23) is valid even for a complex number \(\alpha\) with \({\mathfrak{Re}}[\alpha ]>0\) because the gamma function is analytic in the region \({\mathfrak{Re}}[\alpha ]>0\). In other words, the Schwinger parametrization can be applied for any complex numbers a and \(\alpha\) satisfying \({\mathfrak{Re}}[a]>0\) and \({\mathfrak{Re}}[\alpha ]>0\) as

$$\begin{aligned} \frac{1}{a^{\alpha }} =\frac{1}{\Gamma [\alpha ]}\int _{0}^{\infty }{\text{d}}s\, s^{\alpha -1} {\text{e}}^{-a s},\quad {\mathfrak{Re}}[a]>0 \ \text{and} \ {\mathfrak{Re}}[\alpha ]>0. \end{aligned}$$
(24)

The Fourier-transform version of the parametrization corresponding to the expression (24) can be obtained by replacing a with \(-ia\):

$$\begin{aligned} \frac{i^{\alpha }}{a^{\alpha }} =\frac{1}{\Gamma [\alpha ]}\int _{0}^{\infty }{\text{d}}s\, s^{\alpha -1} {\text{e}}^{i a s}, \quad {\mathfrak{Im}}[a]>0 \ \text{and} \ {\mathfrak{Re}}[\alpha ]>0. \end{aligned}$$
(25)

3.4 Product of a sequence

In this subsection, we consider the process to combine multiple denominator factors into a single power. For each denominator factor \(a_j=d_j+i\varepsilon\), we need a single independent Schwinger parameter \(s_j\) to perform a single Fourier transform in Eq. (25). We may think of the product of a finite sequence \((a_1^{\alpha _1},\ldots ,a_n^{\alpha _n})\) satisfying \({\mathfrak{Im}}[a_j]=\varepsilon >0\) for all \(j=1\) through n. By applying the identity in Eq. (25) for \(a_j\) from \(j=1\) through n, we can parametrize the product of these factors as

$$\begin{aligned} \prod _{j=1}^n\left( \frac{i}{a_j} \right) ^{\alpha _j}= & {} \int _{[0,\infty )} {\text{d}}^n{\varvec{s}}\, \prod _{j=1}^n \frac{1}{\Gamma [\alpha _j]} s_{j}^{\alpha _j-1}{\text{e}}^{ i a_js_j } \\= & {} \int _{[0,\infty )} {\text{d}}^n{\varvec{s}}\, {\text{e}}^{i{\varvec{a}}\cdot {\varvec{s}}} \prod _{j=1}^n\frac{s_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]}, \\{} & {} \quad {\mathfrak{Im}}[a_j]>0 \quad \text{and} \quad {\mathfrak{Re}}[\alpha _j]>0, \end{aligned}$$
(26)

where a bold-italic letter \({\varvec{X}}\) denotes an n-dimensional Euclidean vector whose components are \(X_i\) for \(i=1\) through n and \({\varvec{X}}\cdot {\varvec{Y}}\) is the scalar product of \({\varvec{X}}\) and \({\varvec{Y}}\):

$$\begin{aligned} {\varvec{X}}= & {} (X_1,\ldots ,X_n), \\ {\varvec{Y}}= & {} (Y_1,\ldots ,Y_n), \\ {\varvec{X}}\cdot {\varvec{Y}}= & {} \sum _{j=1}^nX_jY_j. \end{aligned}$$
(27)

Here, the symbol \(\int _{[0,\infty )} {\text{d}}^n{\varvec{s}}\) in Eq. (26) represents the definite multidimensional integral over the Schwinger parameters \(s_j\)’s as

$$\begin{aligned} \int _{[0,\infty )} {\text{d}}^n{\varvec{s}} = \prod _{j=1}^n \int _0^\infty {\text{d}}s_j. \end{aligned}$$
(28)

Readers who want to study the practical use of the parameterization (26) are recommended to refer to the contents involving the alpha representation given in references [28,29,30].

4 Feynman parametrization

In this section, we derive the Feynman parametrization with an arbitrary number of denominator factors and with arbitrary powers in two independent ways: the partial-fraction decomposition and change of variables in the Schwinger parametrization. In those derivations, we employ change of variables by introducing additional delta function as is given in references [35, 36]. The derived parametrization formula coincides with the elementary form of the Feynman parametrization that can be found, for example, in equation (A.39) on p 806 of Peskin and Schroeder [10].

4.1 Partial-fraction decomposition

Feynman parametrization was first introduced in volume 76 of Physical Review in 1949 in equations (14a) and (15a) of Feynman [4] and equation (2.82) of Schwinger [40]. As Feynman wrote ‘suggested by some work of Schwinger’s involving Gaussian integrals’ right after equation (14a) in reference [4], Schwinger introduced the parametrization ahead of Feynman. These early computations involving Feynman parametrization exploited the partial-fraction decomposition,

$$\begin{aligned} \frac{1}{ab}=\frac{1}{a-b}\left[ \frac{1}{b}-\frac{1}{a}\right] , \qquad a,\,b\ne 0\, \quad \text{and} \quad a\ne b, \end{aligned}$$
(29)

which is an elementary algebraic method of breaking a rational function apart. One can think of the right-hand side of Eq. (29) as the result of a definite integral:

$$\begin{aligned} \frac{1}{a-b}\left[ \frac{1}{b}-\frac{1}{a}\right]= & {} \frac{1}{a-b}\left[ \left. -\frac{1}{t}\right| _{t=b}^{t=a}\right] \\ = & {} \frac{1}{a-b}\int _b^a \frac{{\text{d}}t}{t^2}. \end{aligned}$$
(30)

Note that the integral representation in Eq. (30) is valid only when 0 is not included in the integral domain. Changing variables with

$$\begin{aligned} t=b+x(a-b), \end{aligned}$$

where x runs from 0 to 1, we have \({\text{d}}t=(a-b){\text{d}}x\) and obtain the Feynman parametrization of a rational function 1/(ab):

$$\begin{aligned} \frac{1}{ab}= & {} \int _{0}^{1} \frac{{\text{d}}x}{ [xa+(1-x)b ]^{2} } \\ = & {} \int _{0}^{1} {\text{d}}x_1\int _{0}^{1} {\text{d}}x_2\, \frac{\delta (1-x_1-x_2)}{ (x_1a_1+x_2a_2 )^{2} }, \end{aligned}$$
(31)

where \(a_1=a\), \(a_2=b\), and \(x_1=x\). In principle, a and b can be any non-vanishing numbers or functions if 0 does not exist on the line connecting a and b in a complex plane.

As the denominator factors coming from Feynman propagators, a and b are of the form

$$\begin{aligned} a=d_1+i\varepsilon ,\quad b=d_2+i\varepsilon ,\quad \varepsilon \rightarrow 0^+. \end{aligned}$$
(32)

\(d_1={\mathfrak{Re}}(a)\) and \(d_2={\mathfrak{Re}}(b)\) may vanish as we have stated earlier. However, the presence of the tiny imaginary part \(+i\varepsilon\) forces neither a nor b to be equal to 0. Hence, the combined denominator in Eq. (31) never hits 0 because both \(d_1\) and \(d_2\) are real and the imaginary part \({\mathfrak{Im}}[xa + (1-x)b]=\varepsilon\) remains positive definite,

$$\begin{aligned} xa+(1-x)b =xd_1+(1-x)d_2+i\varepsilon . \end{aligned}$$
(33)

We continue to construct the identity for more denominator factors. By making use of the expression in Eq. (31), we combine the first two denominator factors in \(1/(a_1a_2a_3)\):

$$\begin{aligned}{} & {} \frac{1}{a_1a_2a_3}=-\frac{\partial }{\partial {\mathcalligra {a}}} \int _{0}^{1} {\text{d}}x_1\int _{0}^{1} {\text{d}}x_2 \, \frac{\delta (1-x_1-x_2)}{ {\mathcalligra {a}} a_3}, \\{} & {} \quad {\mathcalligra {a}}=x_1a_1+x_2a_2, \end{aligned}$$
(34)

where we have made use of the identity \({\partial }(1/{\mathcalligra {a}})/{\partial {\mathcalligra {a}}}=-1/{\mathcalligra {a}}^2\). We combine the denominator factors in Eq. (34) by making use of the formula (31) once again:

$$\begin{aligned} \frac{1}{a_1a_2a_3}= & {} -\frac{\partial }{\partial {\mathcalligra {a}}} \int _{0}^{1} {\text{d}}x_1\int _{0}^{1} {\text{d}}x_2\, \delta (1-x_1-x_2) \\{} & {} \times \int _{0}^{1} \frac{{\text{d}}y}{ [y {\mathcalligra {a}}+(1-y)a_3]^2} \\= & {} 2\int _{0}^{1} {\text{d}}x_1\int _{0}^{1} {\text{d}}x_2\, \delta (1-x_1-x_2) \\{} & {} \times \int _{0}^{1} \frac{{\text{d}}y\,y}{ [y (x_1a_1+x_2a_2)+(1-y)a_3]^3}. \end{aligned}$$
(35)

The variables of the multiple integral in Eq. (35) are not appropriate for the Feynman parametrization because the sum of the parameters is not equal to 1.

A convenient way to change the variables into the Feynman parameters for the three denominator factors is to insert the unity. A set of Feynman parameters can be \(y_1=yx_1\), \(y_2=yx_2\), and \(y_3=1-y\) whose sum is 1. This unity is the product of the integrals over a new set of Feynman parameters whose integrands are all Dirac delta functions:

$$\begin{aligned} 1= & {} \int _0^1 {\text{d}}y_1\,\delta (y_1-yx_1)\int _0^1 {\text{d}}y_2\,\delta (y_2-yx_2) \\{} & {} \times \int _0^1 {\text{d}}y_3\,\delta (1-y_1-y_2-y_3). \end{aligned}$$
(36)

By multiplying the integrand in Eq. (35) by the unity in Eq. (36) and integrating over \(x_1\), \(x_2\), and y, as is shown in [35, 36], we obtain

$$\begin{aligned}{} & {} \frac{1}{a_1a_2a_3} = 2 \int _0^1 {\text{d}}y_1\int _0^1 {\text{d}}y_2\int _0^1 {\text{d}}y_3\int _0^1 {\text{d}}y \int _{0}^{1} {\text{d}}x_1\delta (y_1-yx_1) \\{} & {} \qquad \times \int _{0}^{1} {\text{d}}x_2\delta (y_2-yx_2) \\{} & {} \qquad \times \frac{y\delta (1-x_1-x_2) }{ [y (x_1a_1+x_2a_2)+(1-y)a_3]^3}\delta (1-y_1-y_2-y_3) \\{} & {} \quad =2 \int _0^1 {\text{d}}y_1\int _0^1 {\text{d}}y_2\int _0^1 {\text{d}}y_3\int _0^1 {\text{d}}y \int _{0}^{1} \frac{{\text{d}}x_1}{y}\delta \left( \frac{y_1}{y}-x_1\right) \\{} & {} \qquad \times \int _{0}^{1} \frac{{\text{d}}x_2}{y} \delta \left( \frac{y_2}{y}-x_2\right) \\{} & {} \qquad \times \frac{y\delta (1-x_1-x_2) }{ [y (x_1a_1+x_2a_2)+(1-y)a_3]^3}\delta (1-y_1-y_2-y_3) \\{} & {} \quad = 2 \int _0^1 {\text{d}}y_1\int _0^1 {\text{d}}y_2\int _0^1 {\text{d}}y_3\int _0^1 {\text{d}}y \frac{ y^{-1}\delta \left( 1-\frac{y_1+y_2}{y}\right) }{ [y_1a_1+y_2a_2 +(1-y)a_3]^3} \\{} & {} \qquad \times \delta (1-y_1-y_2-y_3) \\{} & {} \quad =2 \int _0^1 {\text{d}}y_1\int _0^1 {\text{d}}y_2\int _0^1 {\text{d}}y_3\int _0^1 {\text{d}}y \frac{y^{-1}(y_1+y_2) \delta \left( y-y_1-y_2\right) }{ [y_1a_1+y_2a_2 +(1-y)a_3]^3} \\{} & {} \qquad \times \delta (1-y_1-y_2-y_3) \\{} & {} \quad =2 \int _0^1 {\text{d}}y_1\int _0^1 {\text{d}}y_2\int _0^1 {\text{d}}y_3 \frac{\delta (1-y_1-y_2-y_3) }{ [y_1a_1+y_2a_2 +y_3a_3]^3}, \end{aligned}$$
(37)

where we have made use of the property of the Dirac delta function

$$\begin{aligned} \delta \Big [f(\xi )\Big ]=\sum _j\frac{1}{|f'(\xi _j)|}\delta (\xi -\xi _j). \end{aligned}$$
(38)

Here, \(\xi _j\)’s are simple zeros of \(f(\xi )\).

In this way, we can combine an arbitrary number of denominator factors. By inspection, we find that overall factor 2 and the denominator power 3 in Eq. (37) are correlated. As the number of factors increases by unity, the denominator power also increases by unity. Thus, the denominator power is n and the overall factor is \((n-1)!=\Gamma [n]\) when we combine n denominator factors. Mathematical induction can be applied to verify that for any n, the propagator denominator can be combined as

$$\begin{aligned} \frac{1}{a_1\cdots a_n} =\Gamma [n] \int _0^1 {\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \frac{\delta (1-x_1-\cdots -x_n) }{ (x_1a_1+x_2a_2+\cdots +x_na_n)^n}. \\ \end{aligned}$$
(39)

Note that the parametrization in Eq. (39) holds only if \(\sum _{i=1}^{n}x_i a_i\ne 0\) for all \(x_i\). In our case, that condition is always satisfied because \({\mathfrak{Im}}(a_i)>0\).

4.2 General rule

In a similar way illustrated in Sect. 3.3, we derive a more general form of the Feynman parameterization by taking the partial derivatives of the expression in Eq. (39) with respect to \(a_i\)’s as

$$\begin{aligned}{} & {} \frac{1}{a_1^{\alpha _1}\cdots a_n^{\alpha _n}} = \frac{1}{\Gamma [\alpha _1]\cdots \Gamma [\alpha _n]} \left[ \prod _{i=1}^n\left( -\frac{\partial }{\partial a_i}\right) ^{\alpha _i-1}\right] \frac{1}{a_1\cdots a_n} \\{} & {} \quad =\frac{\Gamma [n]}{\Gamma [\alpha _1]\cdots \Gamma [\alpha _n]} \\{} & {} \qquad \times \int _{[0,1]} {\text{d}}^n{\varvec{x}} \left[ \prod _{i=1}^n\left( -\frac{\partial }{\partial a_i}\right) ^{\alpha _i-1}\right] \frac{\delta \left[ 1-\sum _{i=1}^n x_i\right] }{\left( {\varvec{a}}\cdot {\varvec{x}}\right) ^n} \\{} & {} \quad =\frac{\Gamma [\alpha _1+\cdots +\alpha _n]}{\Gamma [\alpha _1]\cdots \Gamma [\alpha _n]} \\{} & {} \qquad \times \int _{[0,1]} {\text{d}}^n{\varvec{x}}\frac{\delta \Big [1- \sum _{k=1}^n x_k\Big ]\;x_1^{\alpha _1-1}\cdots x_n^{\alpha _n-1}}{\left( {\varvec{a}}\cdot {\varvec{x}}\right) ^{\alpha _1+\cdots +\alpha _n}}. \end{aligned}$$
(40)

Here, \({\mathfrak{Im}}(a_i)>0\) and \(\alpha _i\) are positive integers. The form of the Feynman parametrization in Eq. (40) is consistent with equation (6.42) on p 190 of Peskin and Schroeder [10]. We will show that the parameterization in Eq. (40) is the most general form of the Feynman parametrization applicable to any complex numbers \(\alpha _i\) satisfying \({\mathfrak{Re}}(\alpha _i)>0\).

4.3 Derivation of Feynman parametrization from Schwinger’s

The product of a sequence \(1/\prod _{i} a_i^{\alpha _i}\) can be expressed by the Schwinger parameterization given in Eq. (26) as

$$\begin{aligned} \frac{1}{a_1^{\alpha _1}\cdots a_n^{\alpha _n}} = \frac{1}{i^{N}} \int _{[0,\infty )} {\text{d}}^n{\varvec{s}}\, {\text{e}}^{i{\varvec{a}}\cdot {\varvec{s}}} \prod _{j=1}^n \frac{s_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]}, \end{aligned}$$
(41)

where \({\varvec{a}}=(a_1,a_2,\ldots , a_n)\), \({\varvec{s}}=(s_1,s_2,\ldots ,s_n)\), and

$$\begin{aligned} N=\sum _{i=1}^{n}\alpha _i. \end{aligned}$$

Note that the parametrization is valid only if \({\mathfrak{Im}}[a_j]>0\) and \({\mathfrak{Re}}[\alpha _j]>0\) for all \(j\in \{1,\ldots ,n\}\). The n independent parameters \(s_j\) in Eq. (41) can be scaled with a single dimensionless parameter s as

$$\begin{aligned} s\equiv \sum _{j=1}^n s_j. \end{aligned}$$
(42)

We define an n-dimensional Euclidean vector \({\varvec{x}}\) representing the coordinates of \({\varvec{s}}\) in units of s as

$$\begin{aligned} {\varvec{s}}= s{\varvec{x}},\quad {\varvec{x}}=(x_1,x_2,\ldots ,x_n). \end{aligned}$$
(43)

According to Eqs. (42) and (43), every element \(x_j\) ranges from 0 to 1 and the sum of the components of \({\varvec{x}}\) must be 1:

$$\begin{aligned} x_j\in [0,1]\quad \forall j\in \{1,\ldots ,n\}, \qquad \sum _{j=1}^{n}x_j=1. \end{aligned}$$
(44)

Following the way of changing variables with the Dirac delta function described in references [35, 36], one can implement the requirement (42) into Eq. (26) by multiplying the following integral representation of the unity,

$$\begin{aligned} 1 =\int _0^{\infty } {\text{d}}s\,\,\delta \left[ s-\sum _{j=1}^n s_j\right] =\int _0^{\infty } {\text{d}}s\,\,\delta \left[ s\left( 1-\sum _{j=1}^n x_j\right) \right] . \end{aligned}$$
(45)

Multiplying the integrand on the right-hand side of Eq. (41) by the unity in Eq. (45) and changing the variables as presented in Eq. (44), we find that

$$\begin{aligned}{} & {} \frac{1}{a_1^{\alpha _1}\cdots a_n^{\alpha _n}} = \frac{1}{i^{N}} \int _0^\infty {\text{d}}s\,s^{N} \\{} & {} \qquad \times \int _{[0,1]} d^n {\varvec{x}}\,\, \delta \left[ s\left( 1-\sum _{j=1}^n x_j\right) \right] {\text{e}}^{is{\varvec{a}}\cdot {\varvec{x}}} \prod _{j=1}^n \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]} \\{} & {} \quad = \frac{1}{i^{N}} \int _{[0,1]} d^n {\varvec{x}}\,\, \delta \left[ 1-\sum _{j=1}^n x_j\right] \\{} & {} \qquad \times \prod _{j=1}^n \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]} \int _0^{ \infty } {\text{d}}s\,s^{N-1}{\text{e}}^{-s(\varepsilon -i{\varvec{d}}\cdot {\varvec{x}})}, \end{aligned}$$
(46)

where we have substituted \(N\equiv \sum _{j}\alpha _j\) and \({\varvec{a}}={\varvec{d}}+i\varepsilon (1,\ldots ,1)\). Here, the symbol \(\int _{[0,1]} {\text{d}}^n {\varvec{x}}\) represents

$$\begin{aligned} \int _{[0,1]} {\text{d}}^n {\varvec{x}}\equiv \prod _{j=1}^n\int _0^1{\text{d}}x_j. \end{aligned}$$
(47)

In the second line of Eq. (46), we have pulled out the factor of s from the argument of the Dirac delta function as 1/s by making use of the identity given in Eq. (38). We notice that the integral over s in Eq. (46) is convergent because of the infinitesimally positive real parameter \(\varepsilon\) that comes from the tiny imaginary part of the denominator of the Feynman propagator. Were it not for this \(\varepsilon \rightarrow 0^+\), the s integral would have been divergent.

In order to pull out the complex factor \(\varepsilon -i{\varvec{d}}\cdot {\varvec{x}}\) from the exponential function in Eq. (46), we consider the following complex integral

$$\begin{aligned} I\equiv & {} \lim _{R\rightarrow \infty }\oint _{C} {\text{d}}z\, z^{N-1}{\text{e}}^{-z(\varepsilon -i{\varvec{d}}\cdot {\varvec{x}})}, \end{aligned}$$
(48)

where the contour C shown in Fig. 3 is defined by

$$\begin{aligned} C= C_{0}\cup C_{\phi }\cup C_{R}, \end{aligned}$$
(49a)
$$\begin{aligned} C_{0}= \{z=r|r\, \text{runs from } 0 \text{ to } R \}, \end{aligned}$$
(49b)
$$\begin{aligned} C_{\phi }= \left\{ z=R{\text{e}}^{i\phi }|\phi \, \text{runs from } 0 \text{ to } \phi _{0}\equiv \arctan \frac{{\varvec{d}}\cdot {\varvec{x}}}{\varepsilon } \right\} , \end{aligned}$$
(49c)
$$\begin{aligned} C_{R}= \{z=r{\text{e}}^{i\phi _0}|r \text{ runs from } R \text{ to } 0 \}. \end{aligned}$$
(49d)

Here, we restrict \(\phi _0\) to the region \(\left( -\pi /2,\pi /2\right)\) to make the arctangent uniquely defined. Note that \(|\phi _0|<\pi /2\) because \(\varepsilon \ne 0\) and \({\varvec{d}}\cdot {\varvec{x}}\in (-\infty ,\infty )\).

Fig. 3
figure 3

A diagram of the contour \(C=C_{0}\cup C_{\phi }\cup C_{R}\) given in Eq. (49)

Full size image

For each contour in Eq. (49), we define

$$\begin{aligned} I_{X}\equiv \lim _{R\rightarrow \infty }\int _{C_{X}} {\text{d}}z\,z^{N-1} {\text{e}}^{-z(\varepsilon -i{\varvec{d}}\cdot {\varvec{x}})}, \quad X\in \{0,\phi ,R \}. \end{aligned}$$
(50)

Because the integrand of I in Eq. (48) is an analytic inside the closed contour C, I becomes 0 according to the Cauchy integral theorem:

$$\begin{aligned} I=0=I_{0}+I_{\phi }+I_{R}. \end{aligned}$$
(51)

As is shown in Appendix B,

$$\begin{aligned} I_{\phi }=0. \end{aligned}$$

Substituting 0 for \(I_{\phi }\) in Eq. (51), we get

$$\begin{aligned} I_{0}= & {} -I_{R} \\= & {} \int _{0}^{\infty }\,{\text{d}}r\, r^{N-1}{\text{e}}^{iN\phi _0}{\text{e}}^{-r\sqrt{\varepsilon ^2+({\varvec{d}}\cdot {\varvec{x}})^2}} \\= & {} \frac{{\text{e}}^{iN\phi _0}}{(\sqrt{\varepsilon ^2+({\varvec{d}}\cdot {\varvec{x}})^2})^N} \int _{0}^{\infty }\,{\text{d}}r'\, r'^{N-1}{\text{e}}^{-r'} \\= & {} \frac{\Gamma [N]}{({\text{e}}^{-i\phi _0}\sqrt{\varepsilon ^2+({\varvec{d}}\cdot {\varvec{x}})^2})^N} \\= & {} \frac{\Gamma [N]}{(-i{\varvec{d}}\cdot {\varvec{x}}+\varepsilon )^N} \\= & {} \frac{i^N\Gamma [N]}{({\varvec{d}}\cdot {\varvec{x}}+i\varepsilon )^N}, \end{aligned}$$
(52)

where \(\Gamma [N]\) is the gamma function defined in Eq. (23). By substituting the result in Eq. (52) for the integral in Eq. (46), we finally obtain the general form of the Feynman parameterization

$$\begin{aligned} \prod _{j=1}^n\frac{1}{a_j^{\alpha _j}} =\Gamma [N] \int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \delta \left[ 1-\sum _{j=1}^n x_j\right] \frac{1}{({\varvec{a}}\cdot {\varvec{x}})^N}\prod _{j=1}^n \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]}. \\ \end{aligned}$$
(53)

Note that the expression in Eq. (53) holds for any \(a_j\) and \(\alpha _j\) satisfying \({\mathfrak{Im}}[a_j]>0\) and \({\mathfrak{Re}}[\alpha _j]>0\). Therefore, the same expression in Eq. (40) with the one in Eq. (53) also holds for any complex numbers \(\alpha _i\) satisfying \({\mathfrak{Re}}(\alpha _i)>0\).

As we stated earlier in Sect. 4.2, the derivation of the parametrization in Eq. (40) based on partial derivatives is defined only for positive integers \(\alpha _i\)’s because non-integer powers cannot be generated by partial derivatives in a usual way. Therefore, our derivation of the master formula (53) corresponds to the analytic continuation of the Feynman parametrization in Eq. (40) from positive integers \(\alpha _i\)’s to any complex \(\alpha _i\)’s satisfying \({\mathfrak{Re}}(\alpha _i)>0\).

5 Elementary applications

In this section, we consider elementary applications of our results. The master relation (53) for the product of a sequence contains an integral over the Feynman parameters \(x_i\)’s whose sum is 1. If there is no other \(x_i\) dependence in the integrand, then the integral over the Feynman parameters reduces into a trivial integral involving a combinatorial factor. This is an elementary integral arising in the Dyson series expansion of the time-dependent perturbation theory. In Sect. 5.1, we demonstrate that this integral is expressed as a combinatorial factor \(1/(n-1)!\) if the sequence is the identity sequence of n elements. The derivation of the multivariate beta function from the master relation (53) is presented in Sect. 5.2.

5.1 Combinatorial factor in Feynman-parameter integral

Let us consider the master relation (53) for the product of a sequence with a trivial case of the identity sequence \({\varvec{a}}=(1,\ldots ,1)\) of n elements with unit powers \(\alpha _i=1\) for all i. In that case, the left-hand side of Eq. (53) becomes \(1^n=1\). By substituting the sequence \({\varvec{a}}=(1,\ldots ,1)\) into the integral on the right-hand side of Eq. (53), we have

$$\begin{aligned}{} & {} \Gamma (n)\int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \frac{\delta \left[ 1-\sum _{i=1}^n x_i \right] }{[{\varvec{a}}\cdot {\varvec{x}}]^n} \\{} & {} \quad = \Gamma (n)\int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \frac{\delta \left[ 1-\sum _{i=1}^n x_i \right] }{[x_1+\cdots +x_n]^n} \\{} & {} \quad =\Gamma (n) \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] . \end{aligned}$$
(54)

Therefore, the master relation for that trivial case results in the following integral table

$$\begin{aligned} \frac{1}{\Gamma (n)}= \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] . \end{aligned}$$
(55)

We first check the integral table (55) by computing the integral with an elementary brute-force method without using any advanced techniques. The \(x_n\) integral in Eq. (55) is trivial because of the Dirac delta function. After the \(x_n\) integration, the lower limit of every integral can be fixed to 0. However, the sum of the remaining \(n-1\) Feynman parameters must be 1 because of the Dirac delta function. The upper limit of the \(x_1\) integral can be fixed to 1 at which all of the remaining parameters vanish. Then the upper limit of the \(x_2\) integral is fixed to \(1-x_1\). In a similar manner, the upper limit of the \(x_i\) integral is fixed as \(1-x_1\cdots -x_{i-1}\) for all \(i=1\) through \(n-1\). As a result, the integral in Eq. (55) can be evaluated as

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] \\{} & {} \quad = \int _0^1{\text{d}}x_1\int _0^{1-x_1}{\text{d}}x_2\cdots \int _0^{1-x_1 \cdots -x_{n-2}} {\text{d}}x_{n-1}. \end{aligned}$$
(56)

Because the integrand is 1, the \(x_{n-1}\) integral is trivial

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] \\{} & {} \quad = \int _0^1{\text{d}}x_1\int _0^{1-x_1}{\text{d}}x_2 \\{} & {} \qquad \cdots \int _0^{1-x_1 \cdots -x_{n-3}} {\text{d}}x_{n-2}(1-x_1 \cdots -x_{n-2}). \end{aligned}$$
(57)

The integration over \(x_2\) can be carried out as

$$\begin{aligned} \int _0^{A_{n-3}}\! {\text{d}}x_{n-2}\,A_{n-2}= & {} \int _0^{A_{n-3}}\! {\text{d}}x_{n-2}(A_{n-3}-x_{n-2}) \\= & {} \frac{1}{2}A_{n-3}^2, \end{aligned}$$
(58)

where

$$\begin{aligned} A_{k}\equiv 1-\sum _{i=1}^{k}x_i. \end{aligned}$$

A recursive evaluation of the integrals leads to

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] \\{} & {} \quad = \int _0^1{\text{d}}x_1\int _0^{A_1}{\text{d}}x_2\cdots \int _0^{A_{n-2}} {\text{d}}x_{n-1} \\{} & {} \quad = \int _0^1{\text{d}}x_1\int _0^{A_1}{\text{d}}x_2\cdots \int _0^{A_{k-1}} {\text{d}}x_{k} \frac{1}{(n-k-1)!}A_{k}^{n-k-1} \\{} & {} \quad = \int _0^{1}{\text{d}}x_1\,\frac{1}{(n-2)!}(1-x_1)^{n-2} \\{} & {} \quad =\frac{1}{(n-1)!}, \end{aligned}$$
(59)

which confirms that the integral table (55) is valid.

An alternative expression of the integral table (55) can be derived by performing a change of variables. If we change variables in Eq. (56) as

$$\begin{aligned} u_k=\sum _{i=1}^{k}x_i,\quad k\in \{1,\ldots ,n-1\}, \end{aligned}$$
(60)

then the integral becomes

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] \\{} & {} \quad = \int _0^1{\text{d}}u_1 \int _{u_1}^1{\text{d}}u_2 \cdots \int _{u_{n-2}}^1{\text{d}}u_{n-1} J\left[ \frac{\partial (x_1,x_2,\ldots ,x_{n-1})}{\partial (u_1,u_2,\ldots ,u_{n-1})}\right] , \end{aligned}$$
(61)

where \(J\left[ \frac{\partial (x_1,x_2,\ldots ,x_{n-1})}{\partial (u_1,u_2,\ldots ,u_{n-1})}\right]\) is the Jacobian for \(n-1\) variables. The Jacobian matrix of that transformation is always expressed in an upper triangular matrix

$$\begin{aligned} J\left[ \frac{\partial (x_1,x_2,\ldots ,x_{n-1})}{\partial (u_1,u_2,\ldots ,u_{n-1})}\right] = \left| {\mathcalligra {Det}} \left( \begin{array}{cccc} \frac{\partial x_1}{\partial u_1}&{} \frac{\partial x_1}{\partial u_2}&{} \frac{\partial x_1}{\partial u_3}&{} \cdots \\ 0&{} \frac{\partial x_2}{\partial u_2}&{} \frac{\partial x_2}{\partial u_3}&{} \cdots \\ 0&{} 0&{} \frac{\partial x_3}{\partial u_3}&{} \cdots \\ \vdots &{} \vdots &{} \vdots &{} \ddots \end{array}\right) \right| \end{aligned}$$
(62)

due to the following identity

$$\begin{aligned} \frac{\partial x_{j}}{\partial u_{i}}= \left\{ \begin{array}{ll} 1,&{}\quad \text{for} \ i\ge j\\ 0,&{}\quad \text{otherwise}. \end{array}\right. \end{aligned}$$
(63)

The Jacobian can be evaluated straightforwardly because the determinant of an upper triangular matrix is the product of its diagonal components:

$$\begin{aligned} J\left[ \frac{\partial (x_1,x_2,\ldots ,x_{n-1})}{\partial (u_1,u_2,\ldots ,u_{n-1})}\right] = \prod _{i=1}^{n} \frac{\partial x_i}{\partial u_i} =1^n=1. \end{aligned}$$
(64)

By inserting the Jacobian in Eq. (64) into the one in Eq. (61), we obtain an alternative expression of the integral table (55)

$$\begin{aligned} \frac{1}{\Gamma (n)}= \int _0^1{\text{d}}u_1 \int _{u_1}^1{\text{d}}u_2 \cdots \int _{u_{n-2}}^1{\text{d}}u_{n-1}. \end{aligned}$$
(65)

Additionally, let us perform another change of variables in Eq. (70) as

$$\begin{aligned} t_k=1-u_k,\quad k\in \{1,\ldots ,n-1\}. \end{aligned}$$
(66)

The transformation yields

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] \\{} & {} \quad =\int _0^1{\text{d}}t_1\int _0^{ t_1}{\text{d}}t_2\cdots \int _0^{t_{n-2}} {\text{d}}t_{n-1}. \end{aligned}$$
(67)

Then we can express the integral (67) by making use of the Heaviside step function \(\theta (t)\) defined in Eq. (19) as

$$\begin{aligned}{} & {} \int _0^1{\text{d}}t_1\int _0^{ t_1}{\text{d}}t_2\cdots \int _0^{t_{n-2}} {\text{d}}t_{n-1} \\{} & {} \quad =\int _{[0,1]}{\text{d}}^{n-1}\varvec{t}\, \theta (t_1-t_2) \theta (t_2-t_3)\cdots \theta (t_{n-2}-t_{n-1}) \\{} & {} \quad = \frac{1}{(n-1)!}, \end{aligned}$$
(68)

which can be computed by substituting \(a_i=1\) and \(\alpha _i=1\) in the Feynman parameterization (40). Remarkably, the integral (68) appears in various fields of physics. The time-ordered product appearing in the Dyson series representation for the Schwinger–Dyson equation for the time-dependent perturbation theory [22, 23, 41, 42] indeed has the same integral in Eq. (68). Equation (32) of Dyson [22] and equation (4) of Dyson [23] are the earliest examples. The path-ordered exponential of quantum field theory has the same mathematical structure. Readers are referred to p 85 of Peskin and Schroeder [10] for more detail.

It is worthwhile to mention that the integral (55) can be straightforwardly computed if we apply a combinatorial argument. First of all, the \((n-1)\)-fold multiple integral is the unity if we set all of the limits to \(x_i\) integral as \(x_i\in [0,1]\). In fact, all of the variables \(x_i\)’s can be treated distinctly because any set of variables of equal value does not contribute to the integral since the corresponding integral measure converges to 0. Thus, there are \((n-1)!\) permutations in ordering \((n-1)\) distinct numbers. The product of the Heaviside step functions in the last line of Eq. (55) reflects the fact that only a fraction of \(1/(n-1)!\) of unity contributes to the integral.

5.2 Multivariate beta function

Let us consider a more general case of the master relation (53) for the product of a sequence with an identity sequence \({\varvec{a}}=(1,\ldots ,1)\) of n elements with non-trivial \(\alpha _i\):

$$\begin{aligned} \frac{1}{1^N}=\, & {} \Gamma (N) \int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \delta \left[ 1-\sum _{i=1}^n x_i \right] \frac{1}{({\varvec{a}}\cdot {\varvec{x}})^N} \prod _{j=1}^{n} \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]} \\ =\, & {} \Gamma (N) \int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \delta \left[ 1-\sum _{i=1}^n x_i \right] \frac{1}{[x_1+\cdots +x_n]^N} \prod _{j=1}^{n} \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]} \\ =\, & {} \Gamma (N) \int _{[0,1]} {\text{d}}^n {\varvec{x}}\, \delta \left[ 1-\sum _{i=1}^n x_i \right] \prod _{j=1}^{n} \frac{x_{j}^{\alpha _j-1}}{\Gamma [\alpha _j]}, \end{aligned}$$
(69)

where \(N=\sum _{i} \alpha _{i}\). In that case, we obtain the following integral table

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1\cdots \int _0^1 {\text{d}}x_n \,\delta \left[ 1-\sum _{i=1}^n x_i \right] x_1^{\alpha _1-1} x_2^{\alpha _2-1}\cdots x_n^{\alpha _n-1} \\{} & {} \quad = \frac{\Gamma [\alpha _1]\Gamma [\alpha _2]\cdots \Gamma [\alpha _n]}{\Gamma [\alpha _1+\alpha _2+\cdots +\alpha _n]}, \end{aligned}$$
(70)

which is the multivariate beta function. When \(n=2\), the integral becomes the beta function

$$\begin{aligned} B(\alpha _1, \alpha _2)\equiv \int _{0}^{1} {\text{d}}x_1 x_1^{\alpha _1-1} (1-x_1)^{\alpha _2-1} =\frac{\Gamma [\alpha _1]\Gamma [\alpha _2]}{\Gamma [\alpha _1+\alpha _2]}. \end{aligned}$$

When \(n=3\), the integral is identical to the one appearing in the parametrization of the surface integral on a triangle in the barycentric coordinate system as is shown in references [43, 44]

$$\begin{aligned}{} & {} \int _0^1{\text{d}}x_1 \int _0^1{\text{d}}x_2\int _0^1{\text{d}}x_3\, \,\delta \left[ 1-x_1-x_2-x_3 \right] x_1^{\alpha _1-1} x_2^{\alpha _2-1} x_3^{\alpha _3-1} \\{} & {} \quad = \frac{\Gamma [\alpha _1]\Gamma [\alpha _2]\Gamma [\alpha _3]}{\Gamma [\alpha _1+\alpha _2+\alpha _3]}. \end{aligned}$$
(71)

For example, the integral table given in equation (26) in Ref. [43] corresponding to the surface integral over a triangle in the barycentric coordinate is nothing but the case \(n=3\) and \((\alpha _1,\alpha _2,\alpha _3)=(2,1,1)\) of the integral table (70)

$$\begin{aligned}{} & {} \int _{0}^{1}{\text{d}}\kappa _a \int _{0}^{1}{\text{d}}\kappa _b \int _{0}^{1}{\text{d}}\kappa _c \delta (\kappa _a+\kappa _b+\kappa _c-1) \kappa _i \\{} & {} \quad = \frac{\Gamma [2]\Gamma [1]\Gamma [1]}{\Gamma [4]}=\frac{1}{6}, \end{aligned}$$
(72)

for \(i=a,b,c\). The integral table given in appendix A in Ref. [43] can also be derived from the integral table in Eq. (70) by applying the binomial expansion

$$\begin{aligned}{} & {} \int _{0}^{1} {\text{d}}\kappa _{a} \int _{0}^{1} {\text{d}}\kappa _{b} \int _{0}^{1} {\text{d}}\kappa _{c} \delta (\kappa _{a}+\kappa _{b}+\kappa _{c}-1) (\kappa _{a}-\xi )^p (\kappa _{b}-\eta )^q \\{} & {} \quad =\sum _{j=0}^{p}\sum _{k=0}^{q} \frac{(-1)^{j+k}p!q!}{j!(p-j)!k!(q-k)!} \int _{0}^{1} {\text{d}}\kappa _{a} \int _{0}^{1} {\text{d}}\kappa _{b} \\{} & {} \qquad \times \int _{0}^{1} {\text{d}}\kappa _{c} \delta (\kappa _{a}+\kappa _{b}+\kappa _{c}-1) \kappa _{a}^{p-j} \kappa _{b}^{q-k} \xi ^{j} \eta ^{k} \\{} & {} \quad =\sum _{i=0}^{p}\sum _{j=0}^{q} \frac{(-1)^{j+k}p!q!}{j!(p-j)!k!(q-k)!} \\{} & {} \qquad \times \frac{\Gamma [p-j+1]\Gamma [q-k+1]}{\Gamma [p+q-j-k+3]} \xi ^{j} \eta ^{k} \\{} & {} \quad =\sum _{i=0}^{p}\sum _{j=0}^{q} \frac{(-1)^{j+k}p!q!}{j!k!(p+q-j-k+2)!} \xi ^{j} \eta ^{k}. \end{aligned}$$
(73)

Here, the integral over \(\kappa _i\) in the second line is the case which \(n=3\) and \((\alpha _1,\alpha _2,\alpha _3)=(p-j+1,q-k+1,1)\).

6 Conclusion

We have investigated detailed nature of analytic properties hidden in the derivation of Schwinger and Feynman parametrizations. Although they are originally developed for combining the Feynman propagator factors in loop integrals in perturbative quantum field theory, the formulation is pedagogically useful far beyond the specific applications to quantum field theoretical computations. The extensive employment of the analyticity of a complex function for the derivation provides a wide variety of exemplary problems with which students can deepen their understanding of complex variables.

The tiny imaginary part \(+i\varepsilon\) appearing in the Feynman propagator has a crucial role of restricting the formulation of the amplitude to respect Huygens’ principle of propagating wave of fields. This is not a mere ad hoc prescription but a rigorous use of mathematical identity based on the Cauchy integral theorem. The significance of the presence of the infinitesimally small positive number has been investigated through our evaluations of contour integrals. Mathematically, the parameter provides a stringent condition of our analytic expression strictly convergent to a physical value.

An application of n-dimensional Fourier transform of multiple Heaviside step functions has led to the Schwinger parametrization of the product of numbers. By multiplying a unity that is parametrized by a convolution of the Dirac delta function, we have demonstrated a straightforward way of changing variables, which leads to the gateway to the Feynman parametrization. Such a living example of the Dirac delta function in coordinate transformation does not have to be known exclusively to particle physicists but undergraduate student can enjoy the tool in various practical computations.

We have made use of the master formula of the Schwinger parameterization of the product of a sequence to compute elementary expressions that are pedagogically useful. We have shown that the combinatorial factor is closely related to the time-ordered product by a brutal-force evaluation of an n-dimensional integral of Feynman parameters whose integral is unity. The multivariate beta function derived from the parametrization is particularly useful in carrying out a surface integral in barycentric coordinate system. In conclusion, we have demonstrated through an explicit derivation of the Schwinger and Feynman parametrizations that the formulation contains rich spectrum of analytic techniques as a state of the art.