Skip to main content
SpringerLink
Log in

Parametric Instability Control of Porous Functionally Graded Beam using Piezoelectric Actuators

  • Original Contribution
  • Published:
Journal of The Institution of Engineers (India): Series C Aims and scope Submit manuscript

Abstract

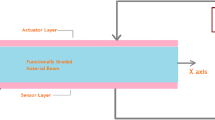
This work presents the active control of parametrically excited porous functionally graded (FG) geometrically nonlinear beam integrated with extensional-mode piezoelectric actuators. The porous FG smart beam is parametrically excited by applying a compressive harmonic load along its axis. The extensional-mode piezoelectric actuators are actuated by applying an extrinsic electric field though negative velocity-feedback control strategy to resist bending deformation in beam. For the corresponding study of active vibration control, a two-dimensional incremental electro-elastic finite element model is derived. The von Karman geometric nonlinearity is accounted for large bending deformation of beam. The corresponding nonlinear finite element governing equations of motion of smart beam are solved in the frequency domain and time domain using harmonic balance method and Bathe time integration method, respectively. The results revealed that the porosity mainly reduces the critical buckling load due to the reduction in flexural rigidity. Further, it induces higher vibration amplitudes of beam or leads to the requirement of higher control electric field. In contrast, the control capability of piezoelectric actuator in controlling parametric instability increases with the porosity. Thus, extensional-mode piezoelectric actuator exhibits the adequate control capability for flexible beams compared to stiffer beams.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. J. Banhart, Aluminum foams: on the road to real applications. Mrs. Bull. 28, 290–295 (2003)

    Article  Google Scholar 

  2. R.M. Mahamood, E.T. Akinlabi, Types of functionally graded materials and their areas of application (Springer, Berlin, 2017), pp.9–21

    Book  Google Scholar 

  3. D. Chen, S. Kitipornchai, J. Yang, Nonlinear free vibration of shear deformable sandwich beam with a functionally graded porous core. Thin-Walled Struct. 107, 39–48 (2016)

    Article  Google Scholar 

  4. D. Chen, J. Yang, S. Kitipornchai, Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 133, 54–61 (2015)

    Article  Google Scholar 

  5. H. Tang, L. Li, Y. Hu, Buckling analysis of two-directionally porous beam. Aerosp. Sci. Technol. 78, 471–479 (2018)

    Article  Google Scholar 

  6. F. Ebrahimi, M. Zia, Large amplitude nonlinear vibration analysis of functionally graded Timoshenko beams with porosities. Acta Astronaut. 116, 117–125 (2015)

    Article  Google Scholar 

  7. S.A. Zahedi, V. Babitsky, Modeling of autoresonant control of a parametrically excited screen machine. J. Sound Vib. 380, 78–89 (2016)

    Article  Google Scholar 

  8. Ewins DJ, Inman DJ. Structural dynamics@2000: current status and future directions. Research Studies Press; 2001

  9. Y. Jia, A.A. Seshia, An auto-parametrically excited vibration energy harvester. Sens. Actuators A Phys. 220, 69–75 (2014)

    Article  Google Scholar 

  10. M. Ghandchi Tehrani, M.K. Kalkowski, Active control of parametrically excited systems. J. Intell. Mater. Syst. Struct. 27, 1218–1230 (2016)

    Article  Google Scholar 

  11. L. Chen, F. He, K. Sammut, Vibration suppression of a principal parametric resonance. J. Vib. Control 15, 439–463 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. L.-W. Chen, C.-Y. Lin, C.-C. Wang, Dynamic stability analysis and control of a composite beam with piezoelectric layers. Compos. Struct. 56, 97–109 (2002)

    Article  Google Scholar 

  13. H. Yabuno, S. Saigusa, N. Aoshima, Stabilization of the parametric resonance of a cantilever beam by bifurcation control with a piezoelectric actuator. Nonlinear Dyn. 26, 143–161 (2001)

    Article  MATH  Google Scholar 

  14. S.S. Oueini, H.A. Nayfeh, Single-mode control of a cantilever beam under principal parametric excitation. J. Sound Vib. 224, 33–47 (1999)

    Article  Google Scholar 

  15. W. Lacarbonara, H. Yabuno, K. Hayashi, Non-linear cancellation of the parametric resonance in elastic beams: theory and experiment. Int. J. Solids Struct. 44, 2209–2224 (2007)

    Article  MATH  Google Scholar 

  16. R.S. Reddy, S. Panda, A. Gupta, Nonlinear dynamics and active control of smart beams using shear/extensional mode piezoelectric actuators. Int. J. Mech. Sci. 204, 106495 (2021)

    Article  Google Scholar 

  17. R. Moradi-Dastjerdi, A. Radhi, K. Behdinan, Damped dynamic behavior of an advanced piezoelectric sandwich plate. Compos. Struct. 243, 112243 (2020)

    Article  Google Scholar 

  18. R. Bahaadini, A.R. Saidi, K. Majidi-Mozafari, Aeroelastic flutter analysis of thick porous plates in supersonic flow. Int. J. Appl. Mech. 11, 1950096 (2019)

    Article  Google Scholar 

  19. N.V. Nguyen, L.B. Nguyen, H. Nguyen-Xuan, J. Lee, Analysis and active control of geometrically nonlinear responses of smart FG porous plates with graphene nanoplatelets reinforcement based on Bezier extraction of NURBS. Int. J. Mech. Sci. 180, 105692 (2020)

    Article  Google Scholar 

  20. K. El Harti, M. Rahmoune, M. Sanbi, R. Saadani, M. Bentaleb, M. Rahmoune, Dynamic control of Euler Bernoulli FG porous beam under thermal loading with bonded piezoelectric materials. Ferroelectrics 558, 104–116 (2020)

    Article  Google Scholar 

  21. Kumar, P, Harsha, A. Vibration response analysis of the bi-directional porous functionally graded piezoelectric (BD-FGP) plate. Mech. Based Des. Struct. 1–26 (2022)

  22. A. Sharma, Effect of porosity on active vibration control of smart structure using porous functionally graded piezoelectric material. Compos. Struct. 280, 114815 (2022)

    Article  Google Scholar 

  23. M.R. Barati, A.M. Zenkour, Electro-thermoelastic vibration of plates made of porous functionally graded piezoelectric materials under various boundary conditions. J. Vib. Control 24, 1910–1926 (2018)

    Article  MathSciNet  Google Scholar 

  24. N. Van Thanh, N.D. Khoa, N.D. Duc, Nonlinear dynamic analysis of piezoelectric functionally graded porous truncated conical panel in thermal environments. Thin Walled Struct. 154, 106837 (2020)

    Article  Google Scholar 

  25. S. Panda, M. Kumar Dubey, A balanced laminate of piezoelectric fiber composite for improved shear piezoelectric actuation of beams. Mech. Adv. Mater. Struct. 27, 1–13 (2019)

    Google Scholar 

  26. C. Pierre, E.H. Dowell, A study of dynamic instability of plates by an extended incremental harmonic balance method. ASME J. Appl. Mech. 52, 693–697 (1985)

    Article  MATH  Google Scholar 

  27. C.T. Sun, X.D. Zhang, Use of thickness-shear mode in adaptive sandwich structures. Smart Mater. Struct. 4, 202 (1995)

    Article  Google Scholar 

  28. T. Iwatsubo, M. Saigo, Y. Sugiyama, Parametric instability of clamped-clamped and clamped-simply supported columns under periodic axial load. J. Sound Vib. 30, 65–77 (1973)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This article is the extended version of the selected presented papers during the International Conference on “Progressive Research in Industrial & Mechanical Engineering” (PRIME-2021).

Funding

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Technology Guwahati, Guwahati, 781039, India

    Rajidi Shashidhar Reddy, Abhay Gupta & Satyajit Panda

  2. Department of Mechanical Engineering, Alliance University, Bengaluru, India

    Abhay Gupta

Authors
  1. Rajidi Shashidhar Reddy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abhay Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Satyajit Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajidi Shashidhar Reddy.

Ethics declarations

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Reddy, R.S., Gupta, A. & Panda, S. Parametric Instability Control of Porous Functionally Graded Beam using Piezoelectric Actuators. J. Inst. Eng. India Ser. C 104, 553–562 (2023). https://doi.org/10.1007/s40032-023-00937-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40032-023-00937-w

Keywords

Search

Navigation