Introduction

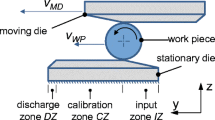
Thread-rolling in a flat die process is a cold-forming process characterised by the use of two dies: one is kept fixed while the other is operated with an alternative work feed. The process is performed in one pass, starting from one end of the fixed die, the work-piece is rolled and deformed as it moves towards the opposite end and ejected. The dies are grooved with a geometry corresponding to the development of the desired thread and inclined by an angle characterising the thread helix. Thus, the tools represent the mirrored geometries of the pieces that will be obtained. The two dies are arranged such that the crests of one are aligned with the grooves of the other. Figure 1 illustrates the process scheme.

Fig. 1
figure 1

Thread-rolling process using flat dies

Full size image

The thread-rolling process has many advantages over machining processes, such as low manufacturing cost, high material utilisation without chipping, superior mechanical properties due to plastic forming, low forming load owing to the incremental process, and high production speed [1]. Hence, the thread-rolling process using flat dies is widely used by the automotive industry.

Various authors have focused their research on thread-rolling topic to improve process simulation accuracy. The three-dimensional numerical modelling of thread-rolling was developed by [2, 3] to analyse the effect of mesh density and states of stress during the process. [4] developed a three-dimensional model of a flat die rolling process incorporating blank rotation, die movement, and pitch angle on die faces. The results showed that deformation was concentrated on the surface and subsurface layers. Moreover, the core was deformed slightly. Based on [4] results, [5] analysed the effect of varying thread form, friction factor, flow stress, and blank diameter on the effective strain and thread height. The research suggested that thread form affects the effective strain generated at the root and crest during rolling. Moreover, the friction factor has little impact on thread form or height at low values, which is typical in cold forming. As the work hardening rate increases, the crest profile tends to change from a concave to a convex shape. [6] focused the research activity the friction coefficient evaluation. They found an experimental friction coefficient (μ = 0.15) using a tribological test. However, assuming higher friction coefficients (μ = 0.30) leads to a better accuracy between the numerical model and experimental measurements. The conflict between the experimentally measured friction coefficients and numerical results was due to the finding that the relative sliding velocity within the contact zone was very low. Hence, the static friction was dominant. Other authors used numerical analysis to improve the process performance [7] that determines the optimal modes for rolling thread on a titanium alloy work-piece. The authors stated that imposing a rolling speed equal to 5.7 m/min increased the product strength up to 30% [8] provided detailed engineering information for the thread-rolling of micro-sized screws. Moreover, they investigated the effect of friction coefficient and relative vertical position between the stationary die and moving die using finite element simulation finding that a shear friction factor of 0.9 is appropriate for preventing slip between dies and raw material. The research also demonstrated that the relative position of the two dies has to be set to the half-length of the pitch to maintain the continuous thread profiles. Evaluation and optimisation of thread forces is another important topic investigated by [9], which presents a novel setup for the direct measurement of forces in thread-rolling operations. This setup allows the measurement of force signals for the feed (z) and radial work-piece (y) directions. [10, 11] proposed an analytical model to predict the maximum load and mode of failure of threaded steel fasteners at high strain rates. The authors demonstrated that several parameters have an influence on the failure mode, such as length of thread engagement, grip length, and strain rate. The threaded assembly tests showed that the number of threads in the grip length changed the failure mode. Moreover, new solutions are available, as studied by [12]. They described a thread-rolling method that consists of thread forming using two flat wedges provided with special grooves designed for thread forming. The shapes of grooves in the cross section correspond to the thread cross-section contour. The advantage of the proposed solution is the possibility of thread forming in any part of shaft.

Motivation

As described in the introduction, a main challenge in the thread-rolling process was to set the numerical software to simulate the process correctly. Particularly, the friction coefficient. Former studies increased the software accuracy, which provided the possibility of using a numerical approach to optimise this process. To increase the knowledge about thread-rolling using flat dies, the authors used a numerical approach to investigate how the die geometry design affects the process. Figure 2 shows a side view of a typical die geometry. As illustrated in the three different zones, the threading step is characterised by the screw being deformed, the finishing step adjusts the desired geometry, and the exit zone allows the screw to be pushed out from the die.

Fig. 2
figure 2

Die design

Full size image

Generally, the main phenomena that affects the tool life in thread-rolling process is die wear. Particularly, the first millimetre is critical because of the amount of deformation induced and the wear experienced. By keeping the die length (LDie) constant, it is possible to increase the threading step to decrease the induced deformation rate. However, this results in the reduction of the finishing step and decreased geometrical accuracy. A trade-off must be identified to achieve good quality parts with less die wear. Starting from an industrial case study, the authors analysed the effect of different sets of threading and finishing cycles in terms of geometrical accuracy, die stress, and wear. The results emphasised the possibility of realising new tool geometry saving cost and achieving good performance in terms of wear and accuracy.

Materials and Methods

In this study, the thread-rolling process of the M9 × 1 screw was selected as a case study because it is used extensively for various applications in the automotive industry. Table 1 lists the geometry and material data of M9 × 1 screws.

Table 1 Thread geometry and material
Full size table

Five different die geometries were designed as a function of threading (Lt_eff) and finishing (Lf) die length. For this research, the authors imposed a constant die length (LDie) and exit zone length (Le) and selected five different Lt_eff and Lf lengths as a function of the number of screw rotations. Coherent with the industrial environment, a total number of 7 screw roll rotations (nTOT) were considered. The steps followed for evaluating the tool die parameters Lt, Lf, and α as functions of screw rotation in the treading (nt) and finish (nf) steps are summarised in Fig. 3.

Fig. 3
figure 3

Scheme of geometry parameter selection

Full size image

Based on the methods shown in Fig. 3, five different values of nt were tested, varying from a minimum of two to a maximum of six screw rotations. Thus, the screw finishing rotation was consequently imposed in the range between five and one rotation. Table 2 shows all the modelled die geometries.

Table 2 Designed tool die geometries
Full size table

To simulate the thread-rolling process, the software COLDFORM by Transvalor was selected. Several preliminary tests were simulated to obtain a good balance between the screw geometry, mesh size, die material, and thread inclination to reduce the simulation time. Additionally, to reduce the computational time, the following constraints were set:

  • The screw height was reduced to 7 mm;

  • The die width (WDie) was set to be 15 mm;

  • An adaptive mesh was adopted, whose element size varied from 2 mm at the boundary to 0.125 mm at the centre;

  • The moving and fixed dies were simulated as rigid;

  • A linear straight thread profile was simulated;

Owing to these assumptions, the simulation time was reduced by 90% (from 522 to 36 h). The final setup based on the preliminary test results is reported in Fig. 4, while Table 3 lists all the other parameters needed to simulate the process. The friction coefficient was set coherently with the data found in the literature [6, 13].

Fig. 4
figure 4

FEM process simulation

Full size image
Table 3 Thread-rolling modelling input parameters
Full size table

The thread-rolling simulation results were compared by considering the part geometry, screw stress, and die wear. The geometrical analysis was set by comparing the part mesh with the final geometry after each screw rotation. The comparison was executed using the commercial software GOM. For stress analysis, the effective stress evaluated according to the von Mises criteria was extracted from the COLDFORM software. The stress experienced on the screw cross section was measured and compared as a function of screw rotation. For die wear evaluation, the software allows an indirect method that is the evaluation of a die damage, a parameter that is function of the stress and the screw/die speed. Die damage is direct proportional to the die wear. Die damage formula is shown in Eq. 1.

$$Die\,damage=\int {\sigma }_{n}\left|{v}_{screw}-{v}_{Die}\right|dt$$
(1)

where:

σn = shear stress [MPa].

vscrew = screw peripheral speed [mm/s].

vdie = Die speed [mm/s].

To evaluate the die damage trend, the thread peak data where higher wear was registered were acquired (Fig. 5a). Three sampling lines were introduced parallel to the thread profile: one located on the peak (line 2) and the other two at a distance of 0.15 mm (line 1) and – 0.15 mm (line 3) from the thread peak. Figure 5b shows the proposed scheme. For each line, a sampling frequency of 0.9 mm was adopted to obtain two hundred samplings per line.

Fig. 5
figure 5

Die damage sampling methods

Full size image

Results

In this section, the main results of the simulated test are reported. Figure 6 shows the evolution of the tread profile on the screw. In Fig. 6, a step dark line was added to highlight the separation between the threading and finishing steps. In particular, in each raw the dark line defines the end of threading and the beginning of finishing. As observed in all tests, the tread profile was obtained after the treading step was in the range of ± 0.05 mm. However, the finishing step does not improve the obtained geometry. Moreover, in all tests, a material increment was recorded on the boundary deformation zone (red zone on the tread side). This phenomenon is a consequence of the constraint imposed for simulation. Furthermore, the single linear tread profile allows the material to flow in that region.

Fig. 6
figure 6

Thread cross-section inspection analysis as a function of number of roll (column) and die geometry (raw), grid spacing (0.5 mm)

Full size image

The effective stress (von Mises) on the screw cross section was analysed after each screw rotation. Figure 7 shows the FEM analysis of all geometries. The maximum value of stress, which changes in the range of 1200–900 MPa was achieved in the last threading step, was located in the screw zone that was in contact with the thread. The main difference observed between the tested geometries is the stress distribution in the screw core: the higher the number of revolution rolls in the treading step, lower the stress registered inside the screw. In the finishing step, a decrease in effective stress, which affected a maximum of 40% of the screw cross section, was observed with the exception of Tests t2_f5 and t3_f4, where high stresses were measured in the first finishing step.

Fig. 7
figure 7

Von Mises stress (MPa) as a function of number of rolls (column) and die geometry (raw)

Full size image

For die wear analysis, the die damage trend evaluated at the thread peak (line 2) at a distance of ± 0.15 mm from the peak (line 1, 3) is shown in Fig. 8 as a function of Lt_eff and Lf. To analyse the results properly, vertical lines were plotted on each graph with the starting/finishing duration of each screw round.

Fig. 8
figure 8

Die damage trend

Full size image

Figure 8 shows the different die damage trend for the tested geometry. In this figure, increasing and decreasing trends can be observed for the finishing step for Tests t2_f5 and t3_f4 (Fig. 8a and b). Apart from the similar trend, Test t2_f5 achieved the highest peak of 600 MPa mm. Test t4_f3 and t5_f2 showed a similar trend characterised by increasing die wear until a value of approximately 300 MPa mm was achieved in the first half screw rotation. Thereafter, the die wear reached a constant trend of 100 MPa mm (Fig. 8c and d). The initial die wear trend of Test t6_f1 is coherent with Tests t4_f3 and t5_f2 with an average peak of 250 MPa mm in the first half round. Thereafter, the average peak decreases to 100 MPa mm. After the first round, die wear has an increasing trend and reaches a peak of 350 MPa mm in the last threading step. Thereafter, a decreasing trend was recorded due to the finishing step.

Discussion

The results of this study regarding the effect of threading and finishing step length in screw production are summarised below:

  • The geometrical analysis after the threading step suggests that each screw was produced correctly. Therefore, the increase in Lt_eff length to obtain a soft deformation does not affect the screw accuracy. Moreover, the geometrical results suggest that it is possible to reduce the finishing step length because only one revolution is sufficient to obtain a screw with a thread in the range of ± 0.05 mm.

  • The stress analysis highlights that the main effect of the different geometries tested is achieved to the screw cross section. Particularly, imposing a gradual deformation (Test t6_f1) resulted in lower stress distribution in the screw core. However, the maximum stress achieved was similar in all tests. This behaviour is coherent with the characteristics of the cold forming process. In thread-rolling, forming forces are generated by the constricting the material to pass through the die gap. Thus, material deformation resistance and rigidity of the machine generates the stress on the dies and work-piece. Since the quantity of material to be deformed is same and the yield value of the processed material is unique for the different configurations, the required strain energies are equivalent and so the maximum stress achieved. Compared to other parameters, die wear was primarily affected by different geometries. From Fig. 8, it can be observed that the deformation induced by the first half round of the threading step on the screw, after which the wear decreases rapidly, is critical for die wear. Additionally, a linearly increasing trend was observed with the slope angle inversely proportional to the Lt_eff length starting from the second threading round.

  • The peak damage registered in the initial round is attributable to the kinematics of the process along that portion of the tool. Furthermore, the screw changes its state from stationary to roto-translatory. Additionally, it can be considered that sliding friction, which is characterised by a static friction coefficient, is present between the part and tool. This phenomenon is coherent with results reported in [6]. However, in the following millimetres, when the screw is in roto-translatory motion and completed the first half revolution, the friction change from static to sliding characterised by a lower coefficient.

To summarise, the main effect due to an increase in the threading step is primarily the reduction of die wear, which is a constant trend except for the first half round. This phenomenon is interesting because reducing the die damage peaks is correlated to die working life. Another important finding is that the die damage reduction is higher between Test t3_f4 and t4_f3, where the acquired peaks change from 500 to 300 MPa mm (40% reduction). This comparison, coupled with the results of geometrical and physical analysis, opens the possibility of eliminating one finishing step to generate a new die design (t4_f2), which decreases material cost by reducing the dimension of the die length.

Conclusion

In this study, the threading and finishing steps of M9 screw production were investigated. The numerical results highlight the deformation-induced impact of die wear. Additionally, the wear trend achieved the peak value in the first screw-half round. Another important result was achieved with respect to the finishing step length. More than two screw rotations could not improve the benefits of the finishing production process. This preliminary study opens the way to redesign the die length by considering a customised die with a specific ratio between the threading and finishing steps.