Transient Stability Assessment of an Alternator Connected to Infinite Bus Through a Series Impedance Using State Space Model

Abstract

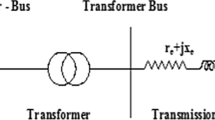
The power angle stability analysis is most important for a grid-connected alternator. This stability may be classified under transient or steady state. The steady state stability may again be classified as static and dynamic. Steady state stability is concerned for slow changes, often in the presence of automatic control systems. Transient stability is the stability of a machine or a group of machines under a sudden impact, e.g., a sudden change in load or a sudden change in generation or in network parameters. The recent practice is to deal with both these problems in terms of state variables for their various advantages. This paper presents the state variable description of an alternator under normal operating conditions and its deviation from normalcy due to a sudden change, e.g., a sudden short-circuit and subsequent operation of the breakers. Then, the power angle swing ($\delta ,\omega$) has been computed using state variables. Infinite bus idealization has been made for the alternator as the capacity of the set (s) is small compared to that of the regional power grid. The classical model based on Park–Gorev transformation has been used to represent the machines. The state space models have been developed from it. The next task is to include the effect of exciter.