Introduction

In the last decades, freshwater supplies have become seriously insufficient because of the excessive use and the increasing pollution of natural water resources (Sharshir et al. 2021a; Kandeal et al. 2021). Also, the global drinking water demand is growing due to the growth of population density and industrial development, but the amount of freshwater is fixed (Shannon et al. 2010; Mevada et al. 2022). Improving the performance of the cleaning water technologies to produce freshwater is a major challenge for the twenty-first century (Elimelech 2006). To overcome that problem, great efforts are being made worldwide to avoid the emergence of this problem while retaining existing restricted drinking water and changing the large quantities of non-potable water that can be obtained through different desalination technologies (Khawaji et al. 2008; Elsaid et al. 2021). Solar still (SS) is one of the best solutions, and methods used for solar desalination to get freshwater in arid regions and have large advantages such as simple in contraction and eco-friendly, but the problem faces the SS is the lower freshwater production (Sharshir et al. 2017a). To enhance the performance of SSs, many researchers’ efforts have been focused on different modifications (Arunkumar et al. 2019b) such as SS integrated with nanoparticles (Elsheikh et al. 2018, 2019a; Sharshir et al. 2018, 2020a), nano-based mushrooms (Sharshir et al. 2021b), energy storage (Yousef and Hassan 2019), coated absorber plate (Thakur et al. 2021a, b), porous absorber (Abdelaziz et al. 2021a), organic colloids (Essa et al. 2020a), glass cover cooling (Elsheikh et al. 2021a; Elmaadawy et al. 2021), sponges (Sellami et al. 2017), wick (Pal et al. 2018), tubular SS (Sharshir et al. 2019a), double-slope SS with rubber scrapers (Elsheikh and Abd 2018), pyramid solar still, evacuated tubes (Sharshir et al. 2019b), adding internal or external condensers (El-Bahi and Inan 1999), adding internal or external reflectors (Sharshir et al. 2021c), applying cooling on the glass cover (Sharshir et al. 2017b), cotton hung pad (Sharshir et al. 2020b), fumed silica nanoparticle in black paint (Sathyamurthy et al. 2020), activated carbon as a porous absorber (Abdelaziz et al. 2021b), bilayered structures (Elsheikh et al. 2022), using hydrogel materials (Sharshir et al. 2020c), nano-based phase change material (Kabeel et al. 2020), stepped basin (Elsheikh et al. 2021b), v-corrugated absorber (Sharshir et al. 2020d), V-type concentrator (Thakur et al. 2021c), painted the still basin with nanomaterials (Kabeel et al. 2019), and so on. It has been illustrated that the depth of the saline water in the SS basin inversely affects the freshwater yield. The control of the water depth to maintain it at a minimum value in the SS is a cumbersome problem. To achieve this purpose, many modifications were proposed such as the use of cubes made of sponge material in the water basin (Rababa’h 2013). Murugavel et al. (2008) studied the SS with various materials integrated with the basin such as cotton, jute, cloth, a porous material, sponge sheet, quartzite, and natural rock. The obtained results showed that the black cotton cloth had the highest yield. The tentative performance of a SS combined with a small-stratum of a thermal material storage beneath the absorber plate in order to produce freshwater during sunset was investigated (El-Sebaii et al. 2009). El-Bialy (2014) experimentally studied a SS with a floating absorber (FA). FA caused a large enhancement in the productivity of the SS. A lot of types of absorbers, for example, stainless steel, copper, aluminum, as well as mica, were used as floating materials for improving the freshwater yield. Samuel et al. (2016) applied different types of low-cost energy storage materials to enhance the freshwater yield. They carried out both experimental and theoretical investigations to evaluate the performance of the SS.

Furthermore, the productivity of the SS is proportional to the evaporation rate which, consequently, is proportional to the surface area of SS. The surface area of water can be increased by using high surface area materials in the SS basin such as wick material. Murugavel and Srithar (2011) applied different materials of wick-like waste cotton pieces, light black cotton cloth, light jute cloth, and sponge sheet in SS to examine its performance. The results reveal that the longitudinally arranged aluminum fins wrapped with black cotton were the maximum influential material among all the different used wick materials, as it generated larger daily yield. Janarthanan et al. (2006) examined a floating wick SS where the water flowed tardily an inclined surface covered with a thin-layer of wick. The little heat capacity of the brine caused a rapid evaporation process. Compared to the basin SS, the time needed to get potable water in a wick SS at the morning was minimized. Moreover, the freshwater yield can be enhanced by about 16–50%. Omara et al. (2013) carried out a hybrid system that consists of a conventional wick SS (CWSS) with a single and double layer of wick integrated with evacuated water collectors. The yield was improved by 114% over traditional still for double-layer square wick (DLSW). Kabeel (2009) designed and fabricated a wick concave SS. A concave-shaped wick surface was used to increase the rate of evaporation with the help of the capillary effect. Results showed that the water yield during the daytime was around 4.1 L/m2. The average efficiency per day was 30%. Alaian et al. (2016) carried out an experimental study to assess the performance of a SS with a developed evaporation surface that consists of pin–fin basin wrapped with a wick. The fins are perpendicularly attached to the SS basin using steel wires. Experiments were examined to investigate the influence of using pin-finned wick on the SS freshwater yield. The use of wick material over the developed fins increased the freshwater yield by larger than 23%. Arunkumar et al. (2019a) conducted the effect of a basin plate coated by CuO nanoparticles only as well as a basin plate coated by a combination of CuO with Polyvinyl Alcohol sponges on the SS productivity. The results illustrated that the still with CuO only improved the productivity by about 39% while the combination enhanced the productivity by about 7.9%. Modia and Modib (2019) examined the performance of a SS using wick materials. The results illustrated that the freshwater output improved by about 18.03% and 21.46% at 1 cm and 2 cm brine depth, respectively.

Because of the need for reliable and accurate modeling of the solar energy systems, ANN models were applied, as a substitute for traditional models (Elsheikh et al. 2019b; Delfani et al. 2019; Motahar and Bagheri-Esfeh 2020; Nasruddin et al. 2018; Kumar et al. 2019). In which, they have been successfully utilized for this objective because of their ability to deal with the extreme uncertainty of these data. ANN has been reported as a robust tool to model different engineering systems (Shehabeldeen et al. 2020, 2019; Essa et al. 2020b; Babikir et al. 2019). Santos et al. (2012) predicted the distillate production of a conventional SS using ANN under the local weather data in Las Vegas, USA, using different parameters such as solar radiation, average daily air velocity, air direction, cloud cover, and air temperature. The results illustrated that with enough input data, the prediction of the SS performance using ANN method works very effectively at various condition parameters. Hamdan et al. (2013) conducted three different ANN models, namely, Nonlinear Autoregressive Exogenous (NARX), Feedforward ANN, and Elman NN to predict a triple SS performance. The experiments were conducted under weather conditions of Jordan. The inputs data were air temperature, solar radiation time, glazier temperature, the water temperature in the upper, middle and lower basin, freshwater output, and plate temperature. Results illustrated that the feedforward ANN is a good tool that used to get the wanted performance. Mashaly and Alazba (2017) developed an ANN model to predict the instantaneous efficiency, water yield, and operational recovery ratio of the inclined SS. The results indicated that the ANN model was accurate and effective in the prediction of the SS performance with tiny errors. Based on Santos et al. (2012) and Hamdan et al. (2013), most of the operational and meteorological parameters that affect evaporation and condensation processes in the desalination unit were not addressed. Moreover, the contribution of all components is not determined in the modeling process.

Due to the requirement for reliable and accurate simulation of the productivity of the wick SS every hour, ANN models have been used to achieve this target. ANN can be trained using a few experimental data, and then, it can learn the nonlinear relationship between the inputs and outputs (El-Said et al. 2021). Once the training process is accomplished, ANN can be used to predict the productivity for any inputs (conditions) that it has not seen before without involving in conducting more experiments or solving complicated mathematical models. Despite the generalization capabilities and robustness of ANN, the traditional ANN still faces some limitations related to the determination of the ANN model parameters. As the determination of ANN model parameters has a significant effect on the performance of the ANN, many methods have been reported in the literature to determine these parameters such as backpropagation (Chen 1990), conjugate gradient (Saini and Soni 2002a), and Quasi-Newton’s method (Saini and Soni 2002b). However, these traditional methods are easy to be stuck in local solution which affects the final quality of the ANN. Therefore, another kind of global optimization methods called meta-heuristic, such as genetic algorithm (Yu and Xu 2014), humpback whale optimizer (Moustafa et al. 2022), equilibrium optimizer (Elsheikh et al. 2021c), parasitism-predation algorithm (Elsheikh et al. 2021d), political optimizer (Elsheikh et al. 2021e), firefly algorithm (Sharshir et al. 2020e), gradient-based optimizer (Elsheikh et al. 2021f), pigeon optimization algorithm (Elsheikh et al. 2021g), moth-flame optimizer (Elsheikh et al. 2021h), and particle swarm optimization (Armaghani et al. 2014), have been proposed.

In the same context, the tree–seed algorithm (TSA) is presented in Kiran (2015) as a meta-heuristic method which simulates the behaviors of trees and their seeds. The TSA has a high ability to balance between the exploitation and exploration of the search space. This has large effect on the performance of the convergence rate and final on the quality of the output. Based on these properties, TSA is used to solve global optimization and constraint optimizations problems (Kıran 2016). This motivated us to use TSA to determine the optimal weights of the ANN, and this leads to improve its prediction.

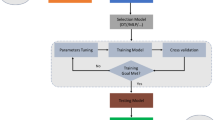
Therefore, the main contribution of this paper is to propose an alternative prediction method to estimate the hourly productivity of the developed wick solar still (DWSS) with copper basin and the conventional wick solar still (CWSS) with steel basin which operated under Egyptian weather conditions. Modeling of this problem using artificial intelligence tools will avoid solving complex mathematical models using cumbersome analytical approaches or time-consuming numerical approaches. The proposed model is called ANN-TSA since it uses the TSA to estimate the weights of the neurons of the ANN model during training process. Then, a set of solutions is generated and each solution represents one ANN with different weights. The quality of ANN is calculated using the objective function, and the optimal ANN model is selected. Thereafter, the solutions of TSA are modified using the TSA operators and repeated the previous procedures until the stop conditions are fulfilled. Then, the best solution is evaluated using the testing set and compute the performance using a different set of measures.

In this study, the ANN-TSA is compared with ANN in which both of them have been developed to predict the hourly productivity based on experimental results. Furthermore, the effect of different input variables on the performance of ANN and ANN-TSA models has been studied. Additionally, the performance of the proposed ANN and ANN-TSA models in forecasting SS performance has been evaluated using different statistical criteria.

The rest of this paper introduces the following:

  • A case study based on north Egypt climate conditions is presented.

  • The experimental setup developed in this study is introduced.

  • Different instruments used in recording and measuring different operational and meteorological are briefly explained.

  • The construction of the developed ANN model is introduced.

  • The algorithm of TSA method is explained.

  • The proposed hybrid algorithm (ANN-TSA) is introduced.

  • The results of the proposed methods are assessed using different statistical criteria, and discussions on these results are presented.

  • Conclusions of the present study have been drawn and presented.

A case study based on north Egypt climate conditions

To demonstrate the performance of the developed models in predicting SS freshwater yield, a case study based on north Egyptian climate conditions has been used in the present work. Meteorological and operational results taken at hourly intervals for about two months at Kafrelsheikh City, Egypt (longitude 30.57°E and Latitude 31.07°N) were used to train the proposed model. For each still, developed wick solar still (DWSS) and conventional wick solar still (CWSS), the input dataset contains ambient temperature, solar radiation, air speed, fed water temperature, wick temperature, water vapor temperature, and the glass temperatures and the output data set contains the hourly productivity.

Materials and methods

Two similar wick SSs have been designed and fabricated as illustrated in Figs. 1 and 2a. The first one is a CWSS with steel basin under the wick material, and the second one is a DWSS with a copper basin under the wick material. The copper basin has enhanced thermo-physical properties compared with steel basin, which enhances the heat transfer process inside the SS. The thermal conductivity of copper basin is higher than that of steel basin by about 700%. The basin area was 0.95 m2 (1 m length × 0.95 m width); the large (back wall) side with the length of 0.44 m and the low (front side) wall with the length of 0.15 m were selected to make a glass angle 30º with the horizontal. This angle is the same as the altitude angle of the experiments place. The backside was made of a U shape with 0.15 m width and 0.20 m height to collect the non-potable water which feed the wick material by capillary action. The basin of the still inclined with an angle of 20° from the horizontal this the best angle according to Omara et al. (2013). The inside walls and basin are painted by black paint to maximize the absorptivity of the solar radiations. All the external walls and basins were isolated and preserved from the open-air by a 30  mm thick of insulation materials (foam sheet) with low thermal conductivity of 0.033 W/m K to decrease the heat losses to the environment. Clear glass covers with 4 mm thickness with high emissivity of about 0.94 were used. Pipes integrated with valves were used to control the feedwater to each still.

Fig. 1
figure 1

Schematic diagram of the experimental setup

Full size image
Fig. 2
figure 2

a Photograph of the experimental setup and, b the samples of seawater were collected from the Mediterranean Sea, Burullus beach

Full size image

The samples of seawater were collected from the Mediterranean Sea, Burullus beach in Kafrelsheikh province using plastic bottles as illustrated in Fig. 2b, and then, they were transported to the supply tank at the research place. The seawater is heated in the SS using solar insolation, the vapor generated inside the still is condensed at the interior face of the glass cover, and the water droplets slide on the interior face of the glass cover. Next, the condensed water is drained into a graduated plastic flask for measuring the amount of condensation.

Measuring instruments

The experimental setup is composed of two wick distillers in addition to suitable instruments to record test data each hour. Test data include the temperature of the air in and out SS, water, and glass cover, in addition to solar radiation, wind velocity, and freshwater productivity. The K type thermocouples were enabled to measure the variations of the temperatures with a range of (− 50 to 180 °C) and accuracy of (± 1 °C), and the digital temperature indicator (model TES-1310) was connected to the thermocouples to measure the temperatures. Four thermocouples were fixed in each still (one of them in the basin with wick materials to measure the wick temperature, one in the glass cove surface to measure the glass temperature, one to measure the vapor temperature inside the still and the final one to measure the water temperature in the still as illustrated in Fig. 2). The solar radiation was measured by a solar power meter (model TES-133R) ranged between (0–2000 W/m2) and accuracy of (± 10 W/m2). It was measured perpendicularly on the glass, which means that it is on the tilted surface at an angle of 30o to find out the amount of solar radiation entering the distillate. Vane anemometer with a digital recorder (model GM816) ranged between (0.1 to 30 m/s), and an accuracy of (± 0.1 m/s) was used to measure wind velocity. The graduated cylinder was used to measure freshwater productivity with an accuracy of (± 2 ml). The uncertainty of length, width, diameter, and thickness measurements were about (± 0.5 mm).

Artificial neural network

Artificial neural networks (ANNs) are a machine learning technique that simulates the biological nervous system. Based on this formulation, the ANNs have been used in several applications including the clustering, classification, and regression. The performance of the ANN depends on the learning process that aims to obtain the optimal weights of the neurons. The Feedforward neural networks (FFNNs) are one of the most popular supervised NNs, which consists of a set of layers; each one of them contains a set of nodes or neurons. Also, each layer is connected to the next layer by a set of weights. In general, the first layer in FFNN receives the input data and passed it to the next layer which called hidden layer (s). Then, each hidden layer takes the output of the previous layer as input until reaching the last layer which called the output layer (Basheer and Hajmeer 2000). Figure 3 shows an example of FFNNs which called Multilayer perceptron (MLP) neural network where the neurons at each layer are interconnected in a one-directional. The output of the \(\ell\)th (\(\ell = 1,2, \ldots ,L)\) layer using the \(i\)th input (\(O_{i}^{\ell }\)) can be formulated as in the following equation

$$O_{i}^{\left( \ell \right)} = \varphi (u_{i}^{\left( \ell \right)} ) = \varphi \left( {\mathop \sum \limits_{j = 1}^{{n_{\ell } }} O_{j}^{{\left( {\ell - 1} \right)}} w_{j,i}^{\left( \ell \right)} + w_{0,i}^{\left( \ell \right)} } \right), \quad 1 \le \ell \le L$$
(1)

where \(L\) and \(n_{\ell }\) are the total number of layers, and the number of neurons at the \(\ell\) th layer, respectively. The \(\varphi \left( . \right)\) represents the activation function of the layer (here, we used a nonlinear tangent hyperbolic function for the hidden layers, and a linear function is used at the output layer). \(w_{j,i}^{\left( \ell \right)}\) represent the weights that connect between the \(i\)th neuron of layer \(\ell\) with the \(j\)th neuron of the previous layer and \(w_{0,i}^{\left( \ell \right)}\) represents the bias of the \(i\)th neuron of the layer \(l\).

Fig. 3
figure 3

The general configuration of MLP NN

Full size image

Tree–seed algorithm

The tree–seed algorithm (TSA) is a meta-heuristic algorithm that emulates behavior of trees and their seeds (Kiran 2015). Where the seeds are used to spread the trees to the surface, then the seed grows and used to produce a new tree. From the optimization viewpoint, the search domain represents the surface, and the solutions of the given problem are represented by the location of tree and seeds. There is a control variable called search tendency (\(ST\)) which used to manage the search process to enhance the convergence.

The TSA is building a location of \(N\) trees (\(X\)) (i.e., the solutions) in the interval [\(L\) \(U]\) (where \(L\) and \(U\) are the lower and upper boundaries) as:

$$X_{ij} = L + r_{1} \times \left( {U - L} \right), \quad i = 1,2, \ldots ,N,\quad j = 1,2,...,{\text{Dim }}$$
(2)

where \(r_{1} \in \left[ {0,1} \right]\) is a random number, while \({\text{Dim}}\) is the dimension of the tested problem.

In general, the TSA has the ability to produce a new seed \(S_{i}\) by using two methods, the first method depends on the best solution \(X^{*}\) and it is defined as:

$$S_{ij} = X_{ij} + \alpha_{ij} \times \left( {X_{ij}^{*} - X_{ij} } \right)$$
(3)

where \(\alpha_{ij}\) is a random number. Meanwhile, the second method depends on the random solution \(X_{r}\) as:

$$S_{ij} = X_{ij} + \alpha_{ij} \times \left( {X_{ij} - X_{rj} } \right)$$
(4)

The parameters \(ST \in \left[ {0,1} \right]\) are used to determine the suitable method to produce a new seed. Moreover, 25% and 10% of the total number of solutions are used as the maximum and the minimum number of generated seeds or trees, respectively.

figure a

Proposed method

The general framework of the proposed approach is given in Fig. 4. In general, the proposed method depends on improving the performance of the ANN by finding the optimal weights using the TSA. The proposed method, called ANN-TSA, consists of two stages, and the first stage aims to find the best weights to reduce the RMSE between the output and its predicted values. Meanwhile, the second stage aims to evaluate the quality of the trained ANN.

Fig. 4
figure 4

The structure of the proposed approach

Full size image

First stage

This stage starts receiving the input dataset and then, divided it randomly into training and test sets. Thereafter, a set of solutions \(X\) is produced which represent the weights of the NN. For each solution \(X\), the fitness function is computed which is defined as

$${\text{RMSE}} = \sqrt {\frac{1}{{N_{S} }}\mathop \sum \limits_{j = 1}^{{N_{S} }} \left( y_{j} - \check{y}_{j} \right)^{2}}$$
(5)

where \(y_{j}\) and \(\check{y}_{j}\) are the output and its prediction value for the \(j\)th sample. The next stage is to determine the optimal solution \(X^{*}\) which has the minimum RMSE value among other solutions. Then, the other solution that is updated using the TSA is repeated until reached to the stop conditions.

Second stage

In this stage, the testing set is applied to the trained NN based on the best solution \(X_{{{\text{best}}}}\). Then, the output is computed, and the quality of the output is evaluated by comparing it with the original target of the testing set.

The performance of the proposed method is evaluated by comparing it with traditional ANN model. However, the process of determining the parameters of TSA is performed by using the trial and error and it has been found that the size of the population is set to 25. Since when it increased the performance it little increase, but the time complexity is increased, and when the size of the population decreased than 25, the performance of the proposed model is degradation. In addition, the maximum iterations number is set to 100.

Results and discussion

The results were measured every hour from 9:00 am to 5:00 pm during the daytime and then, repeated for 9 days. Figure 5 illustrates the sample of the experimental input variables data which depends on the weather conditions and cannot be controlled, namely insolation, ambient temperature, inlet water temperature, and air velocity for the suggested model. The total number of datasets used to train the models is 72. The statistical analysis of the used data is demonstrated in Table 1. The average values of insolation, air velocity, ambient temperature, and inlet water temperature are 827.357 W/m2, 2.363 m/s, 29.867 °C, and 29.186 °C, respectively, with standard deviation of 205.125 W/m2, 0.571 m/s, 1.568 °C, and 1.928 °C, respectively. The numerical range of insolation, air velocity, ambient temperature, and inlet water temperature are 540–1100.95 W/m2, 1.2–3.6 m/s, 26.5–32.5 °C, and 25.2–32.65 °C, respectively. Figure 5a demonstrates a sample of insolation data every hour; the mean insolation was 827.35 W/m2. Figure 5b, d demonstrates a sample of ambient temperature and inlet water temperature every hour; the mean of ambient air and inlet water temperature was 29.86 °C and 29.18 °C, respectively. Furthermore, Fig. 5c illustrates air velocity in m/sec; the mean air velocity was 2.36 m/s.

Fig. 5
figure 5

Illustration of the training-dependent input data variables a insolation, b ambient temperature, c air velocity and d inlet water temperature for the proposed ANN and ANN-TSA model

Full size image
Table 1 Statistical analysis of the input data
Full size table

Furthermore, Figs. 6 and 7 illustrate samples of the data of the dependent variables that were used as inputs during the training process of the suggested model. Figures 6 and 7 show the water temperature, wick temperature, glass temperature, and vapor temperature, for CWSS and DWSS, respectively. The maximum and minimum wick temperature for the CWSS was about 69 and 33 °C, respectively, while the average wick temperature for the CWSS was about 54.61 °C as illustrated in Fig. 6a, the average water temperature for the CWSS was about 52.69 °C as illustrated in Fig. 6b, the average vapor temp. For the CWSS was about 46.73 °C as illustrated in Fig. 6c and the average glass temperature for the CWSS was about 42.19 °C as illustrated in Fig. 6d.

Fig. 6
figure 6

Samples of the dependent variables of DWSS extracted from the training data set: a wick, b water, c vapor, and d the glass temperatures for the proposed ANN and ANN-TSA model

Full size image
Fig. 7
figure 7

Samples of the dependent variables of CWSS extracted from the training data set; a wick, b water, c vapor and d glass temperatures for the proposed ANN and ANN-TSA

Full size image

While the average wick, water, vapor, and glass temperatures for the DWSS were about 64.66, 62.80, 53.12, and 45.12 as illustrated in Fig. 7a–d, respectively, which increased by about 18.4%, 19.18%, 13.67, and 6.94% compared with the CWSS.

The use of copper plate beneath wick material in the DWSS enhanced the total freshwater production by about 50% as illustrated in Table 2. Furthermore, the experimental data were divided into two subsets: the training data subset (90%), and the test data subset (10%). A scatter plot of the experimental data is illustrated in Fig. 8. Figure 9 plots the predicted freshwater yield from the ANN-TSA based on an hourly basis.

Table 2 Illustrate the delay production of the CWSS and MWSS
Full size table
Fig. 8
figure 8

Hourly productivity regression plots for training and test for CWSS using ANN-TSA

Full size image
Fig. 9
figure 9

Hourly productivity regression plots for training and test for DWSS using ANN-TSA

Full size image

In order to assess the performance of the developed models, regression plots for the outputs of the established networks are plotted in Fig. 8 with respect to the desired (actual) outputs for both of the training and testing phases. These plots show a good agreement between the predicted results of the network and actual outputs with high regression values.

Figure 8 shows that the regression values (R) in the testing and training processes of the CWSS are 0.999 and 0.995, respectively, whereas the overall amount of R is 0.997. Furthermore, Fig. 9 illustrates that the R values in the training and testing phases of the DWSS are 1 and 0.964, respectively, whereas the overall amount of R is 0.996. To evaluate the performance of the proposed ANN-TSA model compared with ANN model, the identical dataset is utilized to predict the freshwater yield. Figure 10 shows the experimental data of HP and the predicted HP using the ANN and ANN-TSA. Furthermore, Table 3 epitomizes the seven statistical coefficients of the predicted data by the ANN and ANN-TSA models for the CWSS and DWSS.

Fig. 10
figure 10

HP sample of the experimental data and the predicted data by ANN and ANN-TSA models. a CWSS and b DWSS

Full size image
Table 3 Statistical coefficient for performance estimating ANN and ANN-TSA
Full size table

From Fig. 10 and Table 3, it is observed that the ANN-TSA was more effective than ANN to predict the HP of the CWSS and DWSS. In this study, we used 7 statistical error values to evaluate the two models proposed in this study, namely R2, RMSE, MRE, MAE, COV, EC, OI, and CRM. From Table 3, the R2 for the CWSS are about 0.97 for ANN and 0.99 for ANN-TSA, while for the DWSS are about 0.97 for ANN and 0.98 for ANN-TSA, the higher value of R2 illustrates the better similarities between the experimental and predicted data. Furthermore, the RMSE for the ANN-TSA model (0.0475) is lower than the RMSE got by ANN (0.084) for the CWSS but, for the DWSS the MRSE for the ANN-TSA model (0.108) is lower than the RMSE got by ANN (0.086). However, the MAE for the ANN-TSA model (0.038) is smaller than for the ANN (0.065) for the CWSS. But for the DWSS, the MAE for the ANN-TSS model (0.053) is smaller than ANN (0.103).

Furthermore, the MAE value for the ANN-TSA model (5%) is smaller by about 20% than ANN for the CWSS also, and for the DWSS the MAE value for the ANN-TSA model (8%) is smaller by about 20% than the ANN and the lower values of the RMSE and MAE proof more accurate prediction results.

Furthermore, approaching OI value to 1.0, this means that the ideal fit between experimental and predicted results will occur (Mashaly and Alazba 2016). We can see from Table 3 the OI for the CWSS using ANN-TSA is about 0.96 which is higher than that of the ANN (0.89) by about 7.8%. Also, for the DWSS the value of OI using the ANN-TSA is about (0.93) which is larger than that the ANN (0.89) by about (4.49). The closer CRM is to zero, the better model accuracy. From Table 3, it is noticed that in the case of CWSS the value of CRM is smaller with using ANN-TSA (0.017) than that using the ANN (0.04); however, for the DWSS the value of CRM is smaller with using ANN-TSA (0.008) than that using the ANN (0.054).

The conciliation means that for the ideal data modeling, RMSE, CRM, and MAE must be a minimum value closer to zero; on the other side, the R2, OI should approach to 1 as closely as possible. The present results revealed the excellence of the ANN-TSA model to predict the HP for the CWSS and DWSS compared with the ANN only; however, the CWSS gives a better evaluation and prediction than the DWSS.

Conclusion

In the present study, a comparison between the ANN and ANN-TSA models was developed to predict the performance of a wick SS with steel basin (CWSS) and with copper basin (DWSS) according to hourly productivity (HP). The experimental results reported that the freshwater productivity was improved by about 50% in the case of DWSS compared with CWSS. The input data to the models are uncontrolled data related to the atmospheric conditions, such as insolation, ambient temperature, inlet water temperature and air velocity as well as measured data related to the operating conditions, such as wick temperature, water temperature, vapor temperature, and glass temperature for both of CWSS and DWSS. The R2, RMSE, MRE, and MAE for the proposed ANN-TSA model were 0.99, 0.0475, 0.228, and 0.05 for the CWSS, respectively, but for the DWSS they are 0.98, 0.086, 0.007, and 0.053, respectively. However, the R values for the training, testing, and total processes of the CWSS are 0.999, 0.995, and 0.997, respectively, whereas for the DWSS they are 1, 0.964, and 0.996, respectively.

Furthermore, the present study proved that the ANN-TSA is an effective direction that can be used to predict the HP of the CWSS and DWSS more than the ANN without the need for further experiments, thus saving financial expenses, effort and time.