Introduction

Water contamination with heavy metals is the increasingly spreading problems in the fields of water conservation and safety. It is linked to a variety of human activities, including mining, metal processing, petroleum, and power generation, as well as metal-based pigments, wastes of electroplating, and other kinds of industrial wastes on a smaller scale (Hashim et al. 2011; Faisal et al. 2018, 2020a, 2021; Al-Hashimi et al. 2021; Sharma and Naushad 2020). Cadmium and lead ions have long been a source of concern in the ecosystem due to their toxicity to living things. Cadmium can cause, kidney malfunction, bronchitis, respiratory diseases, and reproduction issues, while lead ions are the reason for the damage of the hepatic, renal, and central nervous system damages, as well as hypertension, decreased cognitive capacity, etc., (Koldabadi et al. 2012).

There are many methods for treating effluents contaminated by metals, but the best method depends on the pollutant concentration and the cost of treatment (Hilal et al. 2012). Chemical precipitation, electroplating, and ion exchange are some of the techniques utilized. Because of its minimal cost, simplest design, operational simplicity, and intolerance to poisonous substances, the adsorption method has emerged as one of the most promising techniques. Activated carbons, which are commonly used for wastewater treatment, cost between $ 1500 and 2000 per ton including 10–15% loss when regeneration is required. The use of cheap sorbents rather than the expensive ones has been extensively studied (Samra et al. 2014). The date stones are the cost-prohibitive source available from over 35 million of palm trees in Iraq according to the Ministry of Agriculture, Iraq. The date stone is the solid part comprising the seed coming from the fruit of the palm trees planted in hot and tropical countries (Samra et al. 2014). Due to the widespread of this solid waste, the exhausted sorbent is not regenerated and the incineration may be the suitable solution for managing of such material; however, the necessity for disposing of produced ash enriched with metal ions in a more secured landfills is recommended (Marques et al. 1999). Many governorates of Iraq have produced huge quantities of date stones reaching 645,000 tons through the summer of 2009 according to the records from Ministry of Planning. The preparation of each ton from date stones after taking the costs of transportation, cleaning, grinding and electrical energy into account requires approximately US$ 300.

Previous studies such as Hansen et al. (2010), Babakhouya et al. (2010), Chatterjee and Schiewer (2011), Saka et al. (2012), Pugazhendhi et al. (2018), Petrella et al. (2018), Mujtaba Munir et al. (2020) have obviously proved the significance of using the most inexpensive and abundant sorbent for the decontamination of metals in the remediation process. In this direction, the removal of lead ions by Antep pistachio (Pistacia Vera L.) shells and applying 3 layers ANN model to estimate the performance of process was implemented (Yetilmezsoy and Demirel 2008). The sorption of cadmium and lead ions onto activated carbons prepared from date stones using different activation methods was tested (El-Hendawy 2009). The bio-sorption of chromium ions in the columns packed with Agave lechuguilla was analyzed (Romero-González et al. 2009). The removal of nickel ions using Aegle marmelos fruit shell as adsorbent in combination with application of ANN model was investigated (Pandharipande and Deshmukh 2013). Pips of olive was added to eliminate of Pb(II) and Cd(II) from polluted water, and evaluation of removal was achieved by set of experimental tests with the aid of ANN model (Faisal and Nassir 2016; Faisal et al. 2020b). Also, different rice wastes, hyacinth roots, neem leaves and coconut shells were applied to remove of Pb(II) from aqueous solution and the behavior of removal has been simulated by ANN (Singha et al. 2015). Leaves of rubber, mango and jackfruit are applied for cadmium remediation from simulated wastewater in the packed bed columns. Results proved that the genetic algorithm (GA) in combination with ANN has a high ability in the prediction of cadmium removal efficiency versus influent variables (Nag et al. 2019). The GA-ANN hybrid system was successfully predicted the removal efficiency of Cr(VI) using mango, jackfruit, and rubber leaves (Nag et al. 2020). Multiple linear regression (MLR) and GA modeling were used to eliminate of Cu(II) by Chitosan-nanoSiO2 nanocomposite from aqueous solution (Bhattacharya et al. 2021).

Formulation of sorption measurements with suitable relationship to determine the contaminant distribution between solid and liquid phases considers a unique topic because this relation can use effectively in the designing of sorption units. Equilibrium isotherm relationship correlated between the contaminant concentrations in the mentioned phases can be formulated by the sorption models like Langmuir, Freundlich, Elovich, Temkin, and others (Hamdaoui and Naffrechoux 2007). Therefore, this work aims to (i) investigate the effective application of date stones as an inexpensive bio-sorbent for eliminating of cadmium and lead ions from the simulated wastewater, (ii) specify the most influential parameter affected on this process based on sensitivity analysis, (iii) use ANN technique for the description of the equilibrium/non-equilibrium bio-sorption process under consideration at different temperatures, (iv) investigate the possibility of incorporating the transport equation with ANN outputs to describe the migration of metal ions measured physically along the column packed with date stones.

Modeling of sorption measurements and contaminant transport

Isotherm models

Isotherms have correlated between the residual concentration of sorbate in the bulk and the magnitude of sorbent that has been sorbed at the surface of the sorbent (Zheng et al. 2009). Langmuir, Freundlich, and others are examples of sorption isotherm models that have been used extensively in previous studies. The model of Langmuir presumes that a sorbate monolayer forms on the sorbent's surface. The Langmuir formula can be written as follows:

$${q}_{e}=\frac{{q}_{m}b{C}_{e}}{1+b{C}_{e}}$$
(1)

where qe is the sorbate concentration partitioned on the sorbent grains (mg/g), Ce is the sorbate concentration at equilibrium (mg/L), qm is the maximum mass of contaminant sorbed per unit mass of sorbent (mg/g), and b is the saturation coefficient (L/mg).

The Freundlich model is distinguished by sorption that continues as the chemical concentration in the water rises, as well as its nonlinear nature. This is can be illustrated in Eq. 2 as follows:

$${q}_{e}={K}_{F}{C}_{e}^{1/n} $$
(2)

where KF is the Freundlich equilibrium constant (mg/mg) and n is the sorption affinity.

The ANN model

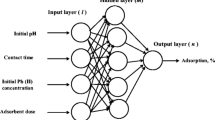
Previous studies introduced the ANNs as an important alternative approach for finding the complex relationship between different operational conditions. This network has a high ability for establishing a relationship between input–output data because it represents an information processing tool. This requires to extract the predominant features from a database that entered such network. ANN includes powerful predictive models to understand, solve and thereby achieve ability for predicting accurately (Yetilmezsoy and Demirel 2008). The working theory of natural networks of biological neurons influenced ANN. A node or neuron is the principal processing element of a neural network. The weighted number of the input signals from the preceding neuron is used to measure the neuron impulse or output of a node. A neuron's learning capacity is achieved by changing the weights in accordance with the selected learning algorithm. The architecture of ANN is composed of input, hidden, and output layers, and the mechanism is iterative. The number of neurons in the output and input layers is proportional to the number of output and input parameters, while in the hidden layer, this number is a crucial decision; however, there is no set formula for determining this number (Kabuba and Bafubiandi 2013).

Contaminant transport equation

Three processes regulate the movement of pollutants in a porous medium: advective–dispersive and sorption of the solute through the reactive matrix. The relationship describing the interaction between the reactive matrix and the solute can be solved simultaneously with transport equation to simulate non-conservative contaminant transport through reactive media. The following is the one-dimensional advection–dispersion equation:

$$n\frac{\partial C}{\partial t}=n{D}_{z}\frac{{\partial }^{2}C}{\partial {Z}^{2}}-n{V}_{z}\frac{\partial C}{\partial Z}-{\rho }_{b}\frac{\partial q}{\partial t}$$
(3)

where Vz is the interstitial velocity and n is the reactive medium's effective porosity, q is the quantity of contaminant sorbed on the reactive matrix. Once taking the sorption isotherms into account and presumably q is a function of C, the transport equation Eq. 3 can be written as:

$$\frac{\partial C}{\partial t}=\left(\frac{{D}_{z}}{R}\right)\frac{{\partial }^{2}C}{\partial {Z}^{2}}-\left(\frac{{V}_{z}}{R}\right)\frac{\partial C}{\partial Z}$$
(4)

where R is the factor of retardation at which:

$$R=1+\frac{{\rho }_{b}}{n}\frac{\partial q}{\partial C}$$
(5)

Equation 4 relates contaminant concentration in the column test to the distance z and subsequent time t. The breakthrough curve resulted from the solution of Eq. 4 and the concomitant plotted curves can be valuable for an optimum design in the sorption process. The S-shaped breakthrough curves for the contaminant effluent from the column depict the breakthrough point at which the mass transfer zone has just reached the tip of the column (Shaverdi 2012). The analytical solution of Eq. 4 is tedious and cumbersome and therefore was formulated and solved by the finite difference numerical method as shown in Eq. 6:

$${C}_{i}^{n+1} = \,{C}_{i}^{n}+\left(\frac{\Delta t}{R }\right)\left({D}_{z}\right){C}_{i}^{n+1}\left(\frac{{C}_{i-1}^{n}-2{C}_{i}^{n}+{C}_{i+1}^{n}}{{\left(\Delta z\right)}^{2}}\right)-\left(\frac{\Delta t}{ R}\right)\left({V}_{z}\right)\left(\frac{{C}_{i}^{n}-{C}_{i-1}^{n}}{\Delta z}\right)$$
(6)

where the scripts n + 1 and n stand for the next and current time interval, respectively; Δt = tn+1 − tn is the size of the time interval as well as the grid notations as i, i + 1, and i−1.

The portion of contaminant retained in the sorbent (described by R in Eq. 6) has been elucidated by the ANN approach. The construction of a computer program to apply the discretized algebraic equations in conjunction with ANN was implemented by MATLAB 7.9.

Materials and methods

Materials

A certain amount of date stones was dried at 100 °C in an oven for almost one day. To achieve a size range of 125 to 710 µm, the stock was pounded and sieved as shown in Fig. 1a. The main characteristics of this material are included: surface area, actual density, apparent density, porosity, cation exchange capacity and initial pH of 0.416 m2/g, 1.418 g/cm3, 0.567 g/cm3, 0.45, 210 meq/100 g and 3.27, respectively. The composition of data stones is included hemicelluloses, cellulose, lignin and ash with percentages of 54, 21, 23, and 1.1%, respectively.

Fig. 1
figure 1

a Physical appearance of date stones before and after grinding, b schematic diagram of column setup used for monitoring the migration of cadmium and lead ions along date stones sorbent

Full size image

Stock solutions of 1000 mg/L cadmium and lead nitrates Cd(NO3)2, Pb(NO3)2 (manufactured by BDH, England) were prepared and adjusted at certain pH value by 0.1 M sodium hydroxide (WTW, Bench model, Germany). The stock solutions that had been intended for the preparation of different concentrations of cadmium and lead ions were kept at 25 °C.

Batch experiments

The main goal of the batch experiments was to determine to what extent the date stones are capable of removing the cadmium and lead ions. To study the sorption trend and obtain the equilibrium sorption isotherm curves, weighed amounts of pounded date stones were brought into contact with 100 mL heavy metal-bearing solution in 250-mL flasks and then vigorously agitated at fixed agitation speed and time. An aliquot of 20 mL was withdrawn to be filtered out via Wattmann filtration paper No.1. The residual out of 10 mL filtrate and the initial contaminant concentrations have been measured via the atomic absorption spectrophotometer (AAS) (Shimadzu, Japan). The quantity of the sorbate retained per unit mass of sorbent was calculated making use of Eq. 7:

$${q}_{e}=\frac{V\left({C}_{i}-{C}_{f}\right)}{m}$$
(7)

The sorption isotherm for \({q}_{e}\mathrm{ as a function of }{c}_{f}\) has consequently been plotted, and the corresponding removal efficacy, Eq. 8, was calculated thereafter:

$$R=\frac{\left({C}_{i}-{C}_{f}\right)}{{C}_{i}}\times 100$$
(8)

Several batch experimental runs were conducted for different bio-sorbent masses from 0.01 to 8 g/ 100 mL, while the values of pH, Ci, contact time, and agitation speed ranged from 2 to 6, 10 to 240 min, 50 to 250 mg/L, and 50–250 rpm. A range of temperatures of 20 to 60 °C were intended to examine the impact of temperature on the bio-sorption process using a shaker (Edmund Buhler SM25, Germany). Each point for sorption measurements is the average for three readings. The percentage of error for these readings was very low (<1%); so, error bars have excluded in the figures related to sorption tests.

Column experiments

Column simulations are a one-dimensional approximation of a real-flow process used to assess the efficiency of reactive media that have been chosen as bio-sorbents based on the extent of contaminant elimination. To simulate and then measure the remedial mechanism inside the reactive substance under consideration, an upward flow column test was conducted and worked with an artificial metal polluted solution. A 50-cm-high, 5-cm-diameter Pyrex column as plotted schematically in Fig. 1b was designed to investigate the contaminant's spatial and temporal migration. Influent fluid was fed upwards from a tank with a steady head which remained constant for each flow rate depended on the usage of constant head tank, pump (CHEM-TECH CTPD4HS1-PAP1-G19 PUMP), valve, and flow meter (Cole-Parmer, model type LZM-6T, China, 0.5 to 4.0 LPM) as clear in Fig. 1b. The flow rate was measured by flow meter and also check by determination the amount of polluted water accumulated in collected tank (Fig. 1b) over a period of time. The column was supplied with ports for sampling at locations measured from the base of bed: P1 (5 cm), P2 (15 cm), P3 (30 cm), and P4 (45 cm).

Owing to the sorption isotherms, all column tests have been conducted at room temperature. The column must be filled with date stones sorbent, and the distilled water was allowed to flow through the packed bed in the upward direction. This type of flow will push the air in front of it to prevent the air entrapment. The constant head feeding tank containing the contaminants (cadmium and lead ions) was to supply the packed column. The contaminant concentrations in water samples collected from the described ports were tracked on a regular basis (almost two days at different periods of time).

Results and discussion

ANN model creation

The performance of cadmium and lead ions removal from water by bio-sorption process was correlated using training algorithm of Levenberg–Marquardt backpropagation (LMA) within ANN model. The MATLAB package version 7.10.0.499 (R2010a) was used to determine this algorithm. The number of layers and nodes with the nature of the transfer functions define the topology of the neural model. The most critical stage in the construction of such model is to optimize the ANN topology, which can be accomplished by splitting the measurements into training, validation and testing subsets.

The first subset can use to assess the network's quality, and the second one is utilized to assess the trained network's performance and generalization capacity. ANN developed in this work depended on the usage of linear transfer function (purelin) and tangent sigmoid transfer function (tansig) at output and hidden layers, respectively. Several conditions like initial concentration, sorbent dose, agitation time, initial pH, number of rpm's, and temperature have all been the input variables to the feed ANN. Furthermore, the performance variable as response was chosen to be the removal efficiency as percentage. In order to optimize the network and as an initial guess, a couple of neurons have been used in the embedded layer such that the number of neurons was eventually expanded before the mean square error (MSE) values were reached (Table 1). Figure 2 reveals how the MSE can be related to the number of neurons for a LMA algorithm.

Table 1 Variation of MSE with neurons number in the training set for (a) cadmium and (b) lead ions
Full size table
Fig. 2
figure 2

Variation of MSE with neurons number at hidden layer for a cadmium and b lead ions using algorithm of Levenberg–Marquardt

Full size image

For developed network, the MSE of cadmium onto date stones sorbent was changed from 0.002 for 2 embedded neurons, as shown in Table 1 and Fig. 2, the MSE decreased significantly to be 0.001 at 4 neurons. An optimum case of eleven hidden neurons was selected as the MSE had been dropped to 0.00031. The rise of the MSE magnitude was as a result of an abrupt change from eleven to sixteen neurons. The features of the MSE output index and the input vector used in this analysis are responsible for this change (Yetilmezsoy and Demirel 2008). Figure 2 shows that for lead ions, the MSE varies in lockstep with the number of embedded neurons, with the strongest value equal to 9.

Since the variations between training error and validation one started to increase and because of the partitioning of the lead and cadmium ions on the date stones sorbent; the training has been terminated after thirty-seven epochs for lead and fifty-four epochs for cadmium. The MSE for the LMA are shown in Fig. 3 as preparation, validation, and evaluation which are chosen according to the highest correlation coefficient values as shown in Fig. 4.

Fig. 3
figure 3

Mean square errors of training, validation, and testing for a cadmium and b lead ions using algorithm of Levenberg–Marquardt

Full size image
Fig. 4
figure 4

Regressions of training, validation, and testing for a cadmium and b lead ions using algorithm of Levenberg–Marquardt

Full size image

Dosage of bio-sorbents and their effects

The effect of date stones sorbent dosages on the removal efficiencies of metal ions adopted in the present tests is investigated at Ci = 50 mg/L, agitation speed = 250 rpm, and time = 1 h for temperature of 25 °C as obvious in Fig. 5a. Results in this figure signified that the percentage removal of Cd(II) ions varied from 10 to 63% due to sorbent mass variation from 0.01 to 5 g for certain Ci. The larger the number of the grams of the sorbent mass, the greater removal is attained (Amarasinghe and Williams 2007). It is evidence that a very marginal change in the sorption efficiencies of Cd(II) ions occurred with changing the bio-sorbent dosage from 5 to 8 g/100 mL; therefore, 5 g/100 mL was selected to conduct other batch experiments. Furthermore, despite a disparity in the value of the better sorbent dose (=5 g/ 100 mL) with the corresponding efficiency of the listed sorbent, Fig. 5b reveals that the lead removal efficiencies into the mentioned sorbent follow the same pattern as previously stated. As a function of bio-sorbent dose, Fig. 5a, b shows a comparison of experimental outcomes and ANN model outputs. Correlation coefficients greater than 0.99 indicate that these two sets of data are in fair agreement.

Fig. 5
figure 5

A comparison between the experimental results and ANN outputs for sorption of cadmium and lead ions onto date stones sorbent as a function of a, b sorbent dosage and c, d initial pH and contact time

Full size image

Contact time and the solution's initial pH

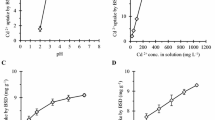
Figure 5 explains the influence of initial pH and contact period on Cd(II) and Pb(II) ion sorption using 5 g of date stones sorbent per 100 mL of polluted solution at 25 °C. The sorption uptake was noticed as high at the early stages of contact time then subsided till reaching equilibrium. This elucidates the availability of the fresh reactive sorption sites earlier. Once theses vacant sites become sorbed with contaminants, no more sorption sites would be ready to receive further contaminants causing a decline in the removal rate (El-Sayed et al. 2010).

The results of the experiments show that the initial pH has a substantial impact on bio-sorption efficiency. At pH 2.0, metal ions were removed owing to the high concentrations of hydrogen ions that have interfered with the ions of metals for binding sites. At pH adjacent to 6, the elimination of metal ions is increased to higher levels, which may be attributed to a reduction in rivalry between hydrogen and metal species for vacant sites (Alkan et al. 2008). The optimum cadmium and lead ion removal efficiencies were clearly reached at an initial pH of 6 and 5, respectively. The findings showed that equilibrium was reached after one hour of agitation and that bio-sorption remained roughly constant as agitation time increased. Over a variety of experiments, a contact time of 10 or 30 min was adequate to achieve equilibrium, implying that the bio-sorption process was conveniently rapid. The time of agitation beyond one hour seems not feasible since similar experimental results are obtained. The ANN model gives a clear explanation for the experimental findings, as shown in Fig. 5, with coefficient of correlation greater than 0.92.

Initial concentration

The best bio-sorbent dose 5 g was added into 100 mL of aqueous phase at the best predetermined pH value to identify the efficiency of Cd(II) and Pb(II) ions removal as varying their initial concentrations from 50 to 250 mg/L. Table 2 explains that the removal efficiencies of metal ions under consideration onto the date stones sorbent were decreased significantly with an increase in the initial metal concentrations. This may result from the significant binding sites present in the bio-sorbent dose chosen. With a coefficient of correlation greater than 0.98, the ANN outputs are consistent with the experimental results for various initial concentrations of adopted pollutants, as exhibited in Table 2.

Table 2 ANN outputs with measurements for removals of cadmium and lead for different initial concentrations at 25 °C (t = 1 h, initial pH = 5–6, and speed = 250 rpm)
Full size table

Agitation speed

Figure 6 explains the change in the removal percentages of Cd(II) and Pb(II) versus the values of agitation speed at the best conditions specified from the previous tests where certain percentage of metal ions (<30%) was removed at zero agitation speed. It is obvious that the sorption rate is directly proportional to the agitation speed and this is due to enhanced mass transfer from the liquid phase to the particles surfaces (Anwar et al. 2010). The measurements show that 100 rpm agitation is necessary to guarantee that all sorption sites are nearly accessible for metal uptake. With a correlation coefficient >0.99, the ANN model provides a strong prediction for the experimental results, as shown in Fig. 6.

Fig. 6
figure 6

ANN outputs and measurements for metals removals due to the variation of agitation speed

Full size image

Temperature

The sorption of Cd(II) and Pb(II) ions onto date stones sorbent was reasonably temperature dependent at an almost one-hour time of equilibrium according to the experimental results (Table 3). As the temperature was raised from 20 to 60 degrees Celsius, cadmium ion sorption rose by 63 to 67 percent, while lead ion reduction percentages remained constant (85–99 percent). This action is perhaps resulted from an improvement in the metal diffusion rate through the external boundary layer and the sorbent particles' internal pores (Alkan et al. 2008). Table 3 shows that the ANN model's projections and the experimental results are in strong agreement with coefficient of correlation of 0.949.

Table 3 ANN outputs with measurements for removals of cadmium and lead for different temperatures (t = 1 h, initial pH = 5–6, dosage = 5 g/100 mL, Ci = 50 mg/L, speed = 100 rpm)
Full size table

Adsorption characteristics

The maximal sorption capacities of date stones sorbent are calculated using equilibrium bio-sorption studies. The isotherms for adopted metals ions have been determined at best values of operational conditions specified previously. Figure 7 plots the sorption isotherms for interaction of metals ions and date stones sorbent using Freundlich, Langmuir and ANN models. To measure the full sorption capacities of date stones sorbent, studies of equilibrium bio-sorption were performed. Isotherms have a fast sorption rate in the early stages and reach asymptotic levels as concentrations increase. In addition to Cd(II), the date stones sorbent has a greater affinitive property towards Pb(II), as shown in Fig. 7. As to the Langmuir equation, the maximum sorption capacity for lead is greater than cadmium as shown in Table 4. The difference in hydration energy between Pb(II) and Cd(II) may explain why Pb(II) is adsorbed better than Cd(II) in this bio-sorbent (Bohli et al. 2013).

Fig. 7
figure 7

Comparison between experimental values of sorbed metal ions (qe) and outputs of ANN, Freundlich, and Langmuir models for ions of cadmium and lead sorbed onto date stones sorbent

Full size image
Table 4 Calculated constants of isotherm models with determination coefficients for bio-sorption of cadmium and lead onto date stones
Full size table

For a number of ex-studies, Table 5 lists the maximum sorption capacity for various inexpensive sorbents. It can be observed from this table that the date stones sorbent has sorption capacity comparable with capacities of other identical bio-sorbents; so, this unique property for such byproduct with its costless can represent the major finding for this study. The usability of an adsorbent for practical applications mainly depends on its recyclability (or regeneration) capacity. However, the regeneration process was not studied in this work because of the costless of date stones sorbent; thus, the disposal of exhausted sorbent in the sanitary landfill considers the optimal solution for dealing with such sorbent. When compared to Freundlich and Langmuir models for describing Cd(II) and Pb(II) bio-sorption onto date stones, Fig. 7 shows that the ANN model matches the experimental results very well. To define the transport of these metal ions in the packed column, the fifth degree polynomial ANN model outputs (Eqs. 9 and 10) are combined with the advection–dispersion equation.

Table 5 Maximum sorption capacities for bio-sorption of cadmium and lead ions onto different sorbents
Full size table
$${q}_{e}=\,0.14\times {10}^{-1}+3.56\times {10}^{-2}{C}_{e}-0.11\times {10}^{-3}{C}_{e}^{2}-4.97\times {10}^{-7}{C}_{e}^{3}+9.4\times {10}^{-9}{C}_{e}^{4}-3.93\times {10}^{-11}{C}_{e}^{5} \mathrm{for cadmium}$$
(9)
$${q}_{e}=\,0.13\times {10}^{-1}+24\times {10}^{-2}{C}_{e}-17.1\times {10}^{-3}{C}_{e}^{2}+18.44\times {10}^{-4}{C}_{e}^{3}-7.85\times {10}^{-5}{C}_{e}^{4}+1.08\times {10}^{-6}{C}_{e}^{5} \mathrm{for lead}$$
(10)

Sensitivity analysis

The sensitivity analysis was performed making use of a matrix of the neural net as well as Garson equation (Eq. 11) to determine the relative value of the input variables. Garson (1991), Aleboyeh et al. (2008):

$${I}_{j}=\frac{{\sum }_{m=1}^{m=Nh}\left(\left(\frac{\left|{W}_{jm}^{ih}\right|}{{\sum }_{k=1}^{Ni}\left|{W}_{km}^{ih}\right|}\right)\times \left|{W}_{mn}^{ho}\right|\right)}{{\sum }_{k=1}^{k=Ni}\left\{{\sum }_{m=1}^{m=Nh}\left(\frac{\left|{W}_{km}^{ih}\right|}{{\sum }_{k=1}^{Ni}\left|{W}_{km}^{ih}\right|}\right)\times \left|{W}_{mn}^{ho}\right|\right\}}$$
(11)

where Ij denotes the jth input variable's relative value to the output variable and Ni and Nh denote the number of input and hidden neurons, respectively. The superscripts o, h, and i as well as subscripts n, m, and k refer to output, hidden, and input neurons, respectively.

In addition to other batch experimental parameters, a 25 percent as relative significance referred to the dominant initial pH parameter for the uptake of Cd(II) ions onto the date stones sorbent, whereas 39% referred to the most influential contact time which has had remarkable impact on the sorption of Pb(II) as shown in Fig. 8. Many studies, on the other hand, have shown that the dominant variable as well as the impact of each variable is strictly dependent upon the experimental ranges utilized in the proposed model (Yang et al. 2014).

Fig. 8
figure 8

Sensitivity analysis for uptake of a cadmium and b lead ions onto date stones sorbent using artificial neural network

Full size image

Transport of metal ions in date stones sorbent packed bed

In this study, a combination of Eq. 6 with Eq. 9 for cadmium and Eq. 10 for lead can be represented by the integrated model developed in this analysis to describe the contaminant transport. To solve the model, the metal concentration is set to zero as an initial state, with a boundary condition of 50 mg/L at the column base and the advective flux for this metal at the column outlet.

The movement of dissolved metals is much restricted throughout the sorbent bed, and this is due to the probable retardation (Fetter 1999). The recovery curves of Cd(II) and Pb(II) ions at the outlets of ports P1 to P4 are plotted in Fig. 9 which reveals a comparison of expected and measured normalized concentrations over time for various flow rates Q = 10 and 20 mL/min. The detention time for the contaminant metals in the thicker sorbent bed is rather longer than that in narrower one making an increase in both the sorption efficiency and the bed longevity. According to the USEPA regulations, the permissible levels of Cd(II) and Pb(II) in potable water shall not reach 0.005 and 0.015 mg/L, respectively (Hashim et al. 2011).

Fig. 9
figure 9

Measured and predicted propagation curves of metals fronts at certain depths along date stones sorbent bed

Full size image

The longer the detention time, the more contaminants are sorbed within the bed. Unfortunately, the more accumulation of these contaminants reduces the retardation factor since they make the pore channels narrower and consequently higher pore water velocity, and thus no more contaminants are retained within the bed. The figure also suggests that the expected and experimental results are in good agreement as estimated from the Willmott’s index in Eq. 12. The index ranging from zero (no agreement) up to 1 (perfect agreement) determines to what extent the predicted (Pi) and observed (Oi) results are in agreement (Krause et al. 2005). Since the Willmott’s index was almost greater than 0.97 in this study, the numerical solution for the model equation is being highly consistent for the contaminants transport within the bed.

$$d=1-\frac{{\sum }_{i=1}^{n}{\left({O}_{i}-{P}_{i}\right)}^{2}}{{\sum }_{i=1}^{n}{\left(\left|{P}_{i}-\overline{O }\right|+\left|{O}_{i}-\overline{O }\right|\right)}^{2}}$$
(12)

Figure 9 illustrates the increase in frontal propagation of the contaminants due to the concomitant in the increase in the volumetric flow rate per bed cross-sectional area. This figure indicates that the binding sites of the date stones sorbent have higher affinity towards lead ions in comparison with that of cadmium ions and these results are consistent with outputs of batch study.

Conclusion

The best batch experimental conditions corresponding to removal of at least 63% of the dissolved Cd(II) and Pb(II) ions over a predetermined optimum 5 g/100 mL date stones sorbent dose were outlined as an initial pH of 5 and 6 for Pb(II) and Cd(II) respectively, with speed of utmost 100 rpm agitation and at room temperature 25 °C. According to the Langmuir sorption equation, the highest sorption capacities of Pb(II) and Cd(II) onto the date stones sorbent were found to be 7.573 and 7.233 mg/g, respectively. To estimate the efficiency of metal ion removal, ANN of 3 layers with linear transfer function (purelin) and tangent sigmoid transfer function (tansig) at the output and hidden layers, respectively, was proposed to yield better guess for six parametric experimental variables corresponding to at least 99% correlation. For ANN, the initial pH of solution and time of contact are corresponding to 25% for Cd(II) and 39% for Pb(II) significant sorption parameter as most dominant experimental parameters. For recovery curves, the ANN outputs have had well agreement with the measured experimental results such that the Willmott’s index had had at least 0.97. The longevity of the sorbent bed decreases with increasing the contaminant velocity through the bed; the thicker the date stones sorbent bed, the higher the removal of the dissolved metal ions. Both expected and experimental findings showed that the binding sites of date stones sorbent have had higher affinity to Pb(II) ions than to Cd(II) ions.